一类时滞区间神经网络的全局鲁棒指数周期性

2010-01-10王晖

成都大学学报（自然科学版） 2010年3期

王晖

(莱芜职业技术学院,山东莱芜 271100)

0 引言

目前,时滞神经网络已经被广泛应用于联想记忆、最优化计算及信息处理等领域中.在这些应用中,平衡点的性质发挥着重要作用.例如,在联想记忆神经网络中,平衡点代表储存的模式,其稳定性意味着储存模式在有噪声的情况下能够被恢复[1].基于此,对平衡点性态的研究一直吸引着广大学者的兴趣.众所周知,平衡点可看作是一种特殊的周期解(任意周期的)[2],对时滞神经网络周期解的研究比对其平衡点的研究更具一般性.然而,在时滞神经网络的大规模集成电路实现过程中,参数的波动是不可避免的.这种情况下,神经网络应该被描述为一个时滞区间神经网络[3-6].因此,对时滞区间神经网络动力行为的研究更具重要意义.本文在不要求激活函数有界、可微和单调的条件下,利用不等式分析技巧和Lyapunov泛函方法讨论了一类时滞区间神经网络的全局鲁棒指数稳定性和周期性,给出了实用有效的判据,推广了有关文献中的结果.

1 预备知识

本文考虑时滞区间神经网络系统模型,

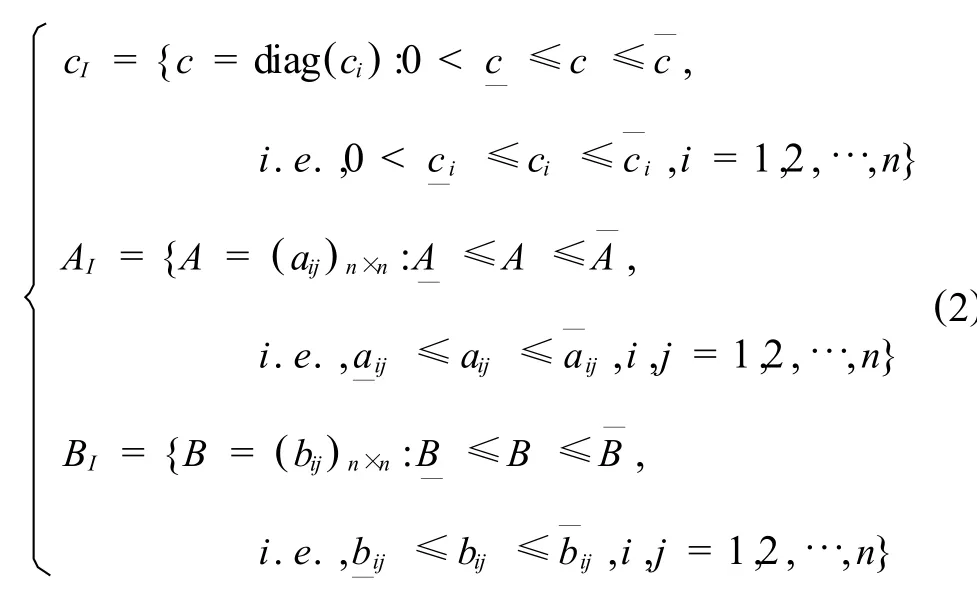
式中,n是网络中神经元的个数,xi(t)是第i个神经元在 t时刻的状态,fj和gj是激活函数,c=diag(ci＞0)、A=(aij)n×n及B=(bij)n×n分别是反馈矩阵和时滞反馈矩阵,τij是信号传输时滞,满足0≤τij≤τ,Ii(t)∶R→R,i=1,2,…,n,都是连续ω周期函数,即,Ii(t+ω)=Ii(t),Øi(t),i=1,2,…,n,是[-τ,0]上的连续函数.

显然,系统(1)的特殊情形为,

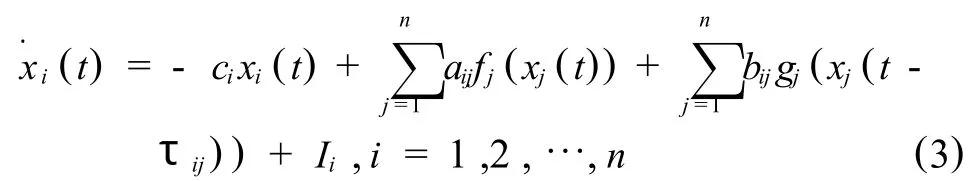
式中,I=(I1,I2,…,In)T为外部常值输入向量.

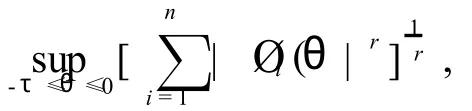
本文要用到如下假定:

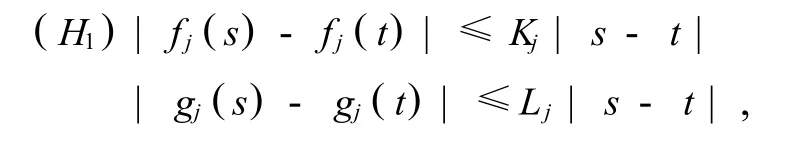
式中,Kj,Lj＞0,∀s,t∈R,j=1,2,…,n.

(H2)存在常数ζkj,ηkj∈R,qk＞0,γi＞0,i,j =1,2,…,n,k=1,2,…,m,使得,

(H3)存在常数γi＞0,i=1,2,…,n,使得,

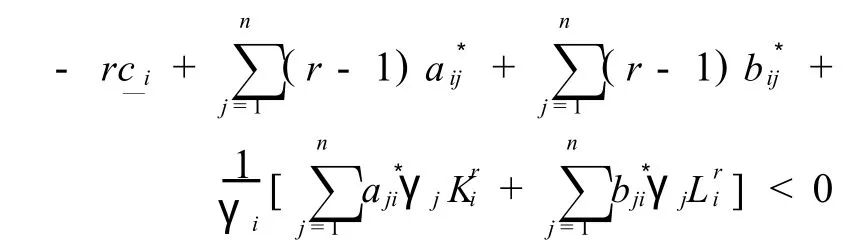
式中,a＊ij=max(|a—ij|,|a—ij|),b＊ij=max(|b—ij|, |b—ij|),i,j=1,2,…,n.

定义1 满足条件(2)的系统(3)称为全局鲁棒指数稳定的,如果 ∀c∈cI,A∈AI,B∈BI,系统(3)的唯一平衡点,x＊= (x＊1,x＊2,…,x＊n)T,是全局指数稳定的,即对系统(3)的任意解x(t),存在常数α≥1,β≥0,使得,

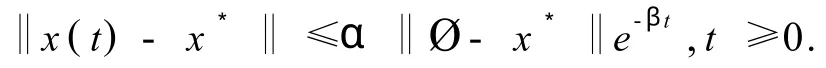
定义2 满足条件(2)的系统(1)称为全局鲁棒指数周期的,如果 ∀c∈cI,A∈AI,B∈BI,系统(1)有唯一的周期解,且当t→+∞时,系统(1)的其他所有解都指数地收敛于该周期解.

引理[7]∀a≥0,bk≥0,k=1,2,…,m,有下面不等式成立,

式中,qk＞0(k=1,2,…,m)是常数,且,

2 主要结果

定理若条件(H1)和(H2)成立,则系统(1)是全局鲁棒指数周期的.

证明 ∀Ø,φ∈C,令,x(t,Ø)=(x1(t,Ø),…,xn(t,Ø))T,x(t,φ) = (x1(t,φ),…,xn(t,φ))T分别表示系统(1)满足初始条件(0,Ø)和(0,φ)的解.定义 xt(Ø)=x(t+θ,Ø),θ∈[-τ,0],t≥0,则,xt(Ø)∈C,t≥0.由式(1)可得,

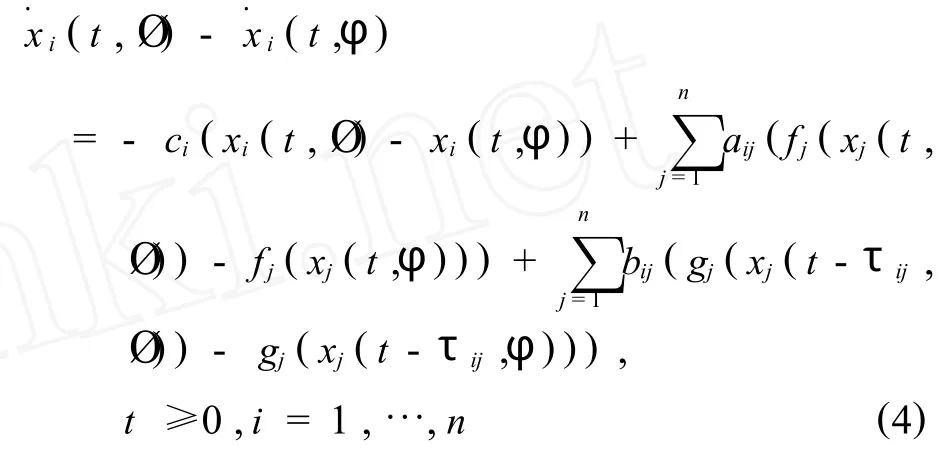
由条件(H2),可选取充分小的ε＞0,使得,

由式(4)和引理有,

考虑Lyapunov泛函,

沿用系统(1)的解计算V(t)的变化率,并利用式(5)和式(6),有,

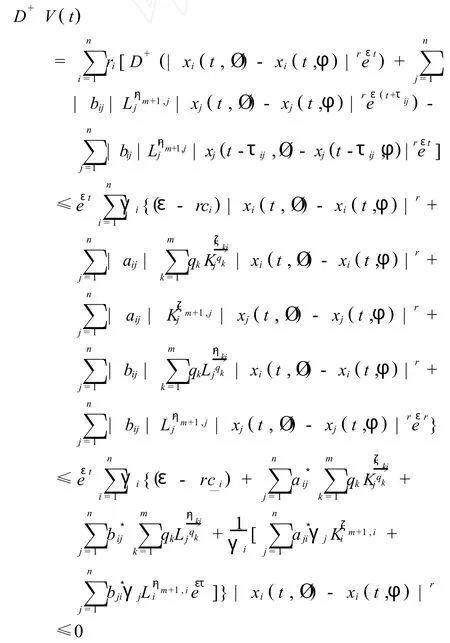
从而,

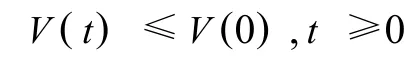
从式(7),可以得到,

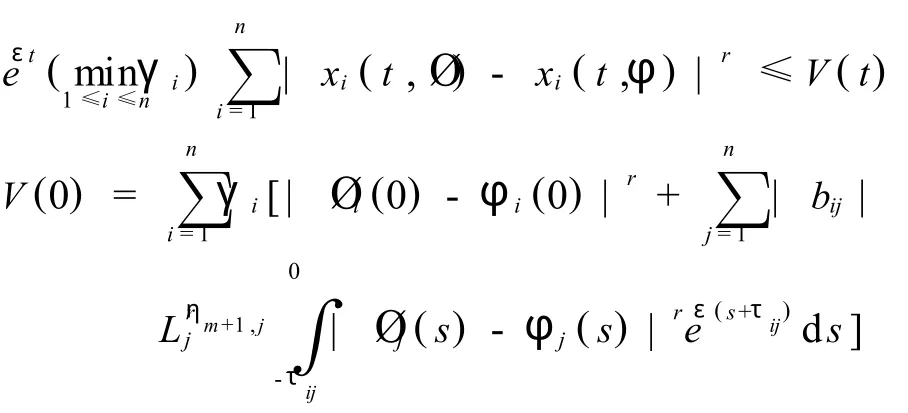
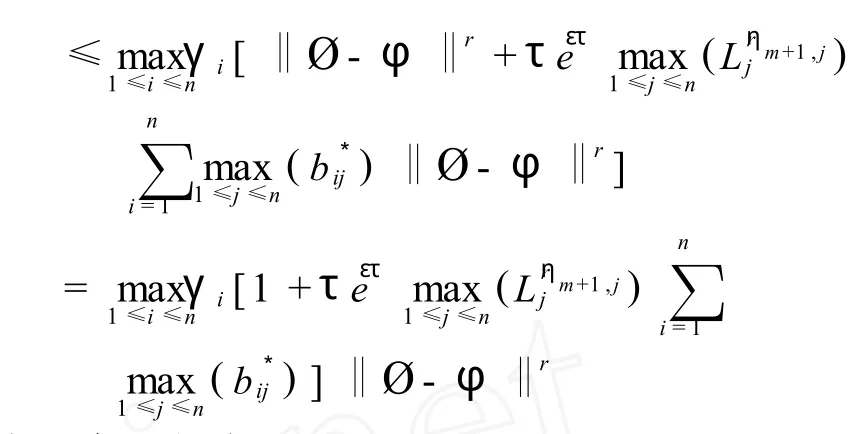
由此容易得出,

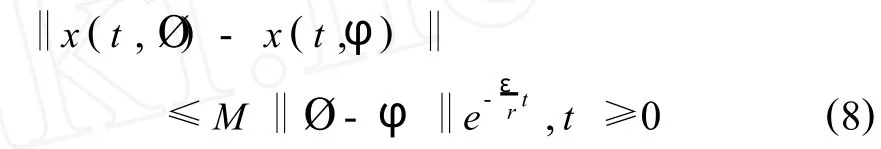
式中,常数

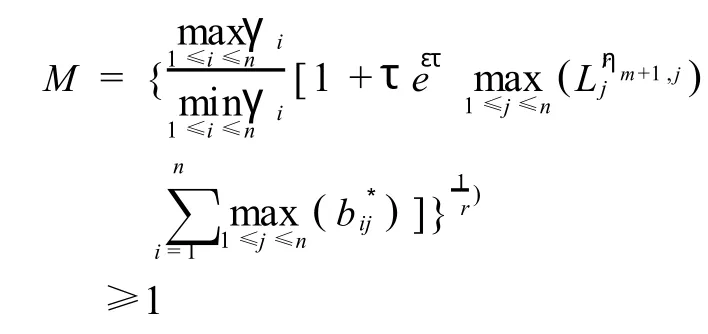
由式(8)可知,

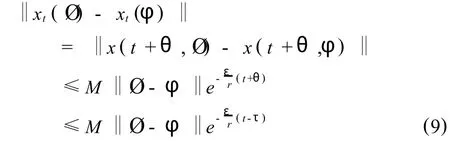
故可以选取正整数m,使得,

定义一个 Poincaré映射 P:C → C,PØ = xω(Ø),则由式(9)得到,

这说明,Pm是一个压缩映射,从而存在唯一的不动点 Ø＊∈C,使得 PmØ＊= Ø＊.又,Pm(PØ＊) = P(PmØ＊) = PØ＊,可知,PØ＊= Ø＊,即, xω(Ø＊)= Ø＊.设 x(t,Ø＊)为系统(1)通过(0, Ø＊)的解,则由已知条件可知,x(t+ω,Ø＊),也是系统(1)的解,且对于 t≥0,有,xt+ω(Ø＊)= xt(xω(Ø＊))= xt(Ø＊).因此,对于 t≥0,有,