协调博弈均衡的稳定性研究
2010-01-02张良桥
张良桥
(1.中山大学岭南学院,广东广州 510275; 2.顺德职业技术学院,广东顺德 528333)*
协调博弈均衡的稳定性研究
张良桥1,2
(1.中山大学岭南学院,广东广州 510275; 2.顺德职业技术学院,广东顺德 528333)*
针对不变突变率模型的缺陷,结合心理学、社会学等成果,通过在吸引域离开阻抗中引入意向因素而拓展了不变突变率模型,研究了意向因素影响下协调博弈均衡的稳定性,探讨了均衡结果与影响因素之间的数量关系,模型可为决策者驾驭经济演化系统提供理论依据。
协调博弈;意向因素;随机稳定状态
一、引言
与新古典经济学不同,进化博弈理论从有限理性参与人群体出发,强调均衡结果的过程依赖性,认为结果是过程的函数,进化博弈为解决均衡选择及均衡稳定性提供了新的视角。到目前为止,在对均衡稳定性的研究中最有代表性的模型是协调博弈模型,最基本的概念是进化稳定策略及随机稳定状态,最核心的标准是风险占优与支付占优。已有对协调博弈均衡稳定性研究的文献主要从实验与理论两方面来进行的:实验研究是针对单个因素来设计情境并探讨其对均衡结果的影响,研究表明,参与人行为选择并不完全取决于基于博弈支付的理性计算,而是受到环境中诸多因素影响;理论研究则通过构建精美的数学模型从数理上探讨参与人行为选择的内在规律性,并用以解释并预测参与人群体行为演化。本文拟在不变突变率模型基础上,结合社会学、心理学及博弈理论的成果,通过引入意向因素来研究协调博弈均衡的稳定性。
二、不变突变率理论研究及其评述
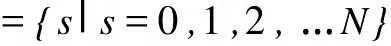

图1 支付矩阵
KMR在达尔文动态基础上引入不随系统状态变化的背景突变因素,令st表示时期t选择策略A的参与者个体数,这样就在状态空间S上定义了马尔可夫链,显然,该马尔可夫链满足遍历性要求并存在唯一平稳分布。在此基础上,KMR采用了Freidlin,M.and Wentzell,A.D.提供的“方向树法”(directed-tree)计算动态过程的平稳分布,并得到“在确定性达尔文动态下,对任何群体规模N≥2,如果由博弈支付完全确定的突变边界s*≠N/2满足s* Young认为由于参与人有高昂的信息搜寻成本,每一个体只能依据非常有限的博弈历史来进行决策[4],因此,均衡的稳定性是由参与人对其他人选择相同行动的信念(即适应性学习过程)决定的。他通过引入参与人对有限博弈历史作出最优反应的适应性动态,采用与 KMR的类似方法研究了离散条件下协调博弈均衡的稳定性,得到“适应性马尔可夫过程的随机稳定状态一定包含在有最小随机潜力的常返集中,并且充分持有的那些状态与试验概率及试验分布无关。”即背景突变保证系统不会离开状态空间的内部,状态空间的边界起着镜面反射作用,在适应性动态下的马尔夫过程满足遍历性要求而使得该过程存在不变分布。 Ellison则是基于标准进化模型即正则扰动而展开的[2]。他在定义常返集吸引域半径及共轭半径的基础上进一步分析得到“如果常返集的并集Ω有R(Ω)>CR(Ω)②,那么,系统的进化稳定集一定包含在Ω中,并且对任何y∉Ω,系统花费在演化路径上的时间为W(x,Y,ε)=O(ε-CR(Ω))。”该结论可表述为:如果某常返状态吸引域半径大于吸引域共轭半径,即离开吸引域的阻抗大于进入吸引域的阻抗(即离开的难度大于进入的难度)时,系统的随机稳定状态一定在此常返状态集之中。协调博弈常返状态集是由严格纳什均衡组成,因此,具有最小随机潜力的严格纳什均衡状态是随机稳定的。 KMR,Young与Ellison都是在保证系统存在常返状态的情况下,求出每个常返状态吸引域的宽度(仅是计算方法不一样),再根据“有最宽吸引域的常返状态就是随机稳定状态”的结论来解决均衡的稳定性问题,其基本思路是: (2)随机因素引入与遍历性。KMR假定状态转移矩阵各元素不为零而保证系统不会被粘住; Young通过假定随机因素的累积作用而保证动态过程满足遍历性要求;Ellison假定样本不完全或者有限记忆保证系统不会被粘住而收敛到严格纳什均衡。有了常返状态存在性与遍历性条件就能保证系统存在平稳分布,于是求随机稳定状态就转化为求动态过程的平稳分布。 (3)形式不同,结论一样。他们所得到的结论核心思想都是一样的,即系统随机稳定状态完全取决于由博弈支付所确定的吸引域宽度。特别地在2×2协调博弈中,吸引域最宽的风险占优均衡是随机稳定状态。 不变突变率假定与现实并不相符合。如果突变来自于试验,那么,有理由相信支付占优均衡会比其他均衡状态的突变率更少;如果突变来自环境约束,那么,随着参与人对环境熟悉程度的提高,其离开相应状态的概率就应该更少;如果突变来自于参与人经验不足,那么,博弈重复次数越多,策略选择中随机因素的影响就会越少,即突变率会随着系统演化时间的推移而减少。博弈论实验也表明参与人行为选择结果会随着环境因素的变化而变化,要更好地描述系统演化就必须基于可变突变率来研究。 首次对不变突变率假定提出挑战的是Bergin and Lipman,他们认为系统在不同状态的突变率应该是不同的,要准确地研究系统的稳定性就必须深入到系统突变产生的过程中去[5]。Bergin and Lipman构建了随状态变化且满足遍历性要求的突变模型,并得到“确定性动态与引入随状态变化突变率的随机动态有相同极限分布”的结论。因此,在动态过程中引入突变是不会起到精炼纳什均衡作用的。不过,他们的模型虽然得到了突变率影响均衡稳定性的结论,但并没有考察突变过程与均衡结果之间的具体关系,缺乏应用性。 Jack Robles认为突变率趋于零的速度对均衡稳定性的影响是非常重要的[6],如果随机动态满足遍历性要求,那么,突变率趋于零时系统就会达到长期均衡,其结论与常突变率模型的极限行为是一样的。于是,他采用了非平稳马尔可夫链及历史依赖的遍历性概念,来研究突变率随时间变化的情形并得到“突变率并不能决定系统的最终状态,随机稳定状态依赖于系统初始条件”的结论。然而,他并没得出随机稳定状态与突变率收敛零的速度之间的具体关系。 尽管可变突变率模型可以更现实地考察参与人行为演化,但也存在固有缺陷:一是这些模型没有区分不同影响因素;二是可变突变率模型没能结合到现实中参与人行为,没有结合社会学、心理学等的研究成果,仅仅从数理上给予描述,具有理论研究意义但难以解释现实人的行为。 [48] Michael R. Pompeo, “America’s Indo-Pacific Economic Vision,” Indo-Pacific Business Forum, U.S. Chamber of Commerce, Washington D.C. July 30, 2018, https://www.state.gov/secretary/remarks/2018/07/284722.htm. 参与人之间两两随机配对进行博弈,行动集为{A,B},博弈支付矩阵见图1。作为基础,假定系统仅存在不变的背景突变因素,根据进化稳定状态的定义可以计算确定动态下系统的突变边界 k*③的值,其中k*表示选择策略A的个体数。由计算可知,突变边界完全取决于博弈支付,并且在支付一定的情况下,博弈最终结果仅依赖于系统初始状态。如果初始时选择策略A的个体数少于 k*,那么,所有参与人最终都选择策略B;反之,如果初始时选择策略A个体数大于k*,那么,系统就会趋于所有人都选择策略A。因此,在确定性动态下,演化系统的均衡结果依赖于系统初始状态,这就是经济学理论中所说的路径依赖(见图2)。 图2 确定性动态下系统演化相图 为了便于研究,把影响系统演化的因素分为背景突变因素与意向突变因素:(1)把使参与人行为发生非系统性偏离的因素称之为背景突变因素。与生态演化现象相比,参与人决策系统会面临更为复杂的确定性或随机性因素影响。因此,在经济系统中引入不随系统状态变化而变化的背景突变率是必要的。(2)把使参与人行为发生系统性偏离的因素称之为意向突变因素。经济系统中参与人的选择是有设定目的的,并且目的性本身必须通过因果过程来解释[7]。实验研究也表明,参与人的有限理性、所处环境的复杂性及意识行为等都可能影响系统演化结果。为简化处理,仅引入三类意向因素:一是参与者个体数。选择某种策略的参与者个体数越多,参与人陷入信息陷阱而选择同样行动的可能性就越大,即个体离开当前状态的概率与所处状态个体数反相关(如羊群行为)。二是博弈支付。参与人倾向于选择支付较高的状态,个体离开当前状态的概率与所处状态支付反相关(经济人假定)。三是偏好程度。参与人的偏好随如广告、舆论、宣传等环境因素的变化而变化,状态之间的转移概率与参与人对所处状态的偏好正相关。 分两步引入随机影响因素。第一步,引入不变的背景突变率ε,并由此得到突变边界,即把非均衡路径上的支付纳入到模型中来;第二步,引入意向因素,得出不同常返状态的离开阻抗。在分析方法上与传统理论文献一样,假定进入常返状态是由背景突变引起的,离开常返状态取决于离开阻抗。图1所示的协调博弈中严格纳什均衡A与B就是动态系统的两个常返状态,参与人对两个常返状态A、B的偏好程度分别用λA、λB(λi>0;i=A,B)表示。偏好参数λ可随广告、宣传、舆论等外界环境变化而变化,λi(i=A,B)值越大,参与人离开当前状态的可能性就越少。 基于Ellison模型的研究思路,下面考察常返状态A的离开阻抗。假定初始时所有参与人都处于状态B,即系统稳定于常返状态B,那么,第一个选择状态A的参与转而选择状态B的突变率为μa×1×λA,其中μ(0<μ<1)是非常少的正数,第二个选择状态A的参与人转而选择B的突变率为μa×2×λA;第三个选择状态A的参与人转而选择状态B的突变率为μa×3×λA,依此类推,第 k个选择状态A的参与人转而选择状态B的突变率为μa×k×λA,a为参与人所处均衡状态A的支付,k为选择当前均衡状态A的个体数, λA为参与人对状态A的偏好程度。显然,μ的指数越大,参与人离开当前状态的可能性就越少。按同样的推理逻辑,可考虑状态B的情形,第k个选择状态B的参与人转而选择状态A的突变率可以记为μd×k×λB。由 Ellison吸引域半径的定义可知,μ的指数与相应状态吸引域半径及离开阻抗正相关。当模型中μ的指数为 1时,就对应于 KMR,Young及Ellison等不变突率理论模型。可以看出,按上述方法引进意向因素并不会改变有限状态马尔可夫过程正则性④的三个条件。首先,引入意向因素并没有改变马尔可夫链的齐次性;其次,背景突变率的存在保证了马尔可夫链遍历性要求;第三,意向因素引入只是使状态之间转移概率发生了线性变化,这就相当于对转移概率进行重标度。所以,引入意向因素后的马尔可夫过程存在平稳分布。 传统动态模型引入随机因素是为了使系统在常返状态之间跳动,便于确定马尔可夫链的平稳分布,但没能把影响参与人行为的复杂因素纳入到模型当中[8]。事实上,影响参与人行为选择的因素是多种多样的,系统随机稳定状态并不完全由博弈支付所确定,与其他许多因素相关。拓展后模型不仅把博弈均衡支付、非均衡支付纳入到模型当中,还考虑到如广告、舆论、宣传等影响参与人均衡偏好程度的社会、心理因素,能够更现实地考察群体行为演化规律。 传统不变突变率模型引入随机因素只是为了使得系统不会被粘住,无法给出状态特别是中间状态到意向状态之间的转移成本,上述拓展后模型可以很方便地计算系统所处中间状态来到意向状态的逆转成本,为决策者选择使系统向意向均衡演化的最低成本措施提供理论依据,如图3。 图3 中间状态转移图 图3中,C点表示目前有k 由此可得“系统偏离高效率常返状态的个体数h越大、所处常返状态的支付越大、对所处状态的偏好程度越高,那么,要使系统转向另一常返状态的逆转成本就会越大。”如果系统已经向非意愿均衡演化,那么,随着时间的推进,选择非意愿均衡的个体数就会不断增加,有利于该状态的利益集团就会慢慢形成,从而使系统转向意愿均衡所需转移成本就会越来越大。因此,管理者在采取措施时,不但要考虑到系统所处的状态与意向状态之间的关系,而且要及时纠正不利于系统演化的各种决策,做到防患于未然,使系统以最小成本达到最有效率的状态。 不变背景突变率模型的结论表明:除博弈支付外,其他任何影响因素都不会使参与人行为发生系统性偏离。现实中体制转轨、文化形成、时尚变化等影响因素的变化都会引起参与人行为发生系统性偏离。因而,把使参与人行为发生系统性偏离的因素纳入到模型中会更现实,可以更好地描述经济系统的演化规律。以上结合社会学的“惯习”、“羊群行为”等现象,通过引入影响离开阻抗的因素来改变系统常返状态的吸引域宽度,进而确定系统的随机稳定状态,拓展了不变突变率模型,得到“均衡结果不仅依赖于博弈支付,而且依赖于达到均衡过程中的影响因素,不同影响因素会使经济演化系统收敛到不同的均衡”的结论。拓展后模型引进了外生影响参数,增加系统的可驾驭性,为制度设计、战略管理等提供理论依据。 值得一提的是,由于作者水平有限,这些模型还没能一般化,有待于进一步探索,另外,使参与人群体行为发生非系统偏离的意向因素还有许多,针对不同的模型如何引进还需更详细的探讨与研究。 注释: ①为便于说明,以下字母A既表示状态(A,A),又表示策略A;字母B既表示状态(B,B),又表示策略B。 ②其中R(Ω)为并集Ω的吸引域的半径,Ω为共轭半径。 ③k*包涵了非均衡路径上支付对均衡的影响。 ⑤事实上,传统方法通过折现因子把时间纳入到模型中,并比较现值与收益流来决定参与人的行为选择。 ⑥从状态x首次回到常返状态Ω的期望等待时间与maxx∈zW(x, Ω,ε)=limε→0Ο(ε-CR(Ω))正相关。其中 CR(Ω)表示常返状态Ω的共轭半径,也就是说,从常返状态Ω外的任何状态 x出发,都可以找到对应的 T,在 T时期回复到Ω的概率至少是ε-CR(Ω)阶,花费在Ω之外的期望时期数至少大于 k2ε-CR(Ω)。直观含义是,在两常返状态系统中,进入阻抗越大,花费在演化路径上的时间就会越长。 [1]Kandori,M.,Mailath,G.J.,rob,R..Learning,Mutation, Long-run equilibria in games[J].Econometrica,1993,(61):29-56. [2]Ellison,G..Basins of Attraction,Long-run stochastic stability, and the speed of step-by-step evolution[J].Review of economic studies,2000,(67):17-45. [3]Freidlin,M.I,Wentzell.Random perturbations of dynamical systems[M].Berlin/New York:Springer-verlag,1984. [4]Young,H.P..The evolution of conventions[J],Econometrica,1993,(61):57-84. [5]Bergin,J.,Lipman,B..Evolution with state-dependent mutations[J],Econometrica,1996,(64):943-956. [6]Robles,J..Evolution with changing mutation Rates[J].Journal of economics theory,1998,(79):207-223. [7]Hodgson,G.M..Darwinism in economics:from analogy to ontology[J].Journal of Evolutionary Economics,2002,(12): 268-279. [8]张良桥.论博弈均衡与随机稳定状态[J].财经理论与实践, 2007,28(4):87-91. On the Stochastic Stability of Equilibrium in Coordination G ame ZHANG Liang-qiao1,2 (1.L ingnan College,Zhongshan University,Guangzhou,Guangdong 510275,China; 2.Economic Department S hunde Polytechnic college,Shunde,Guangdong 528333,China) To overcome the shortcomings of constant mutation rate model,we extend traditional theoretical models by incorporating background mutation and deliberation mutation into resistance,which is suggested by literatures in psychology and sociology.Multiple equilibriums under the influence of stochastic deliberation factors are studied systematically as well.Afterwards, we investigate quantitively the relation between the equilibrium outcomes of coordination games and the corresponding affecting factors.Conclusions drawn from our model can offer theoretical foundations for decision makers to manage economic evolutionary systems. Coordination Game;Deliberation Factor;Stochastic Stability F019.1 文献标识码: A 文章编号:1003-7217(2010)06-0083-05 2010-04-19 国家社科基金(09ZDB17&09ZDB18)、广东省自然科学基金(05300601) 张良桥(1968—),男,湖南祁阳人,中山大学经济学博士生、顺德职业技术学院副教授,研究方向:博弈论、进化博弈理论。 (责任编辑:子衿)三、可变突变率理论研究及其评述
四、基于背景突变因素与意向突变因素理论模型拓展


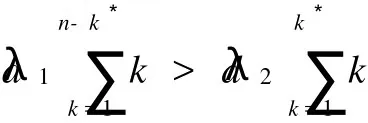
五、系统中间状态到意向状态的演化时间与演化成本
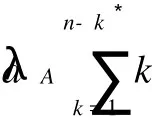


六、小结与后续研究展望