基于星敏感器的两种姿态确定算法比较分析

史广青，卢 欣，武延鹏，黄 欣，王 立

（北京控制工程研究所，北京100190）

基于星敏感器的两种姿态确定算法比较分析

史广青，卢 欣，武延鹏，黄 欣，王 立

（北京控制工程研究所，北京100190）

介绍了星敏感器的两种姿态确定算法：最小二乘算法和QUEST算法，推导了最小二乘算法和QUEST算法求解三轴姿态的公式；比较了两种算法在不同恒星数目下的计算精度以及在全天区范围内的计算精度；利用实例说明QUEST算法不仅在全天区范围内姿态计算精度高于最小二乘算法，而且在观测星数量较少，且观测星座呈现较为不利的构型时仍然具有较高的计算精度.

星敏感器；QUEST算法；最小二乘算法

星敏感器是航天应用中最精确的姿态测量光学传感器.它利用恒星星光方向矢量分别在惯性参考坐标系下的指向和在星敏感器坐标系下的指向两方面信息，求得从惯性系到星敏感器坐标系的方向余弦矩阵，从而可以确定航天器在惯性参考系下的指向.

星敏感器的信息处理可以分为星点提取、星图识别、姿态确定三个模块.

利用星图识别的结果，计算得到航天器姿态矩阵的过程称为姿态确定.当前的姿态确定算法主要有q-法、QUEST算法、ESOQ法、ESOQ2法、SVD法和最小二乘算法.文献［1-3］对前5种算法的鲁棒性、计算精度、计算时间等都做了比较充分的比较.

本文利用恒星观测矢量，比较和分析了最小二乘算法和QUEST算法的精度，并给出了实际的应用，为星敏感器姿态确定算法的优化提供了参考依据.

1 算法介绍

1.1 最小二乘算法介绍

最小二乘算法是TRIAD算法改进而来［4］.

定义参考矢量阵为V3×n＝（V1V2...Vn），观测矢量阵为W3×n＝（W1W2...Wn），多矢量的观测方程可写为

式中，A为姿态矩阵，观测方程代数解可表示为

在一般情况下，上式解A为非正交矩阵，正交化后的姿态阵A*的计算公式如下：

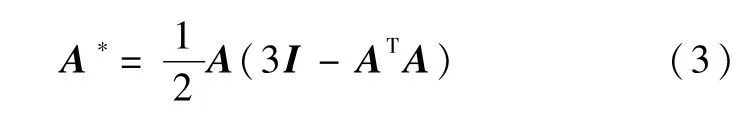
式中I为三阶单位矩阵.

1.2 QUEST算法介绍

QUEST算法来源于q-法，它将求解Wahba最小损失函数的问题［5］转化为求解矩阵特征值的问题，矩阵的最大特征值对应的特征矢量为最优姿态四元数.

根据Wahba损失函数，满足公式（1）的姿态矩阵，是使损失函数

达到的最小的解.式中ai是一组加权系数.将加权系数归一化，姿态确定问题转化为使增益函数

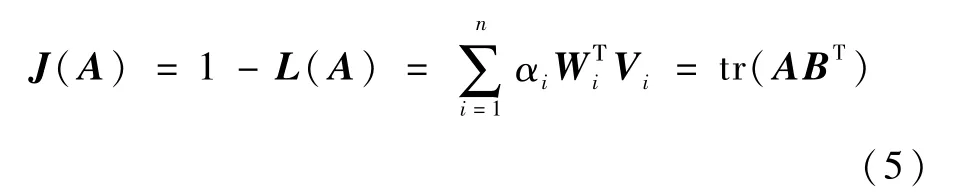
将姿态矩阵A写成四元数形式

式中，I3×3为单位矩阵，q＝［q1q2q3q4］T＝是四元数，ε是四元数的矢量部分，η＝q4是四元数的标量部分，ε×为反对称矩阵.

将增益函数J（A）化成关于姿态四元数q的一个二次型函数，并进一步化简

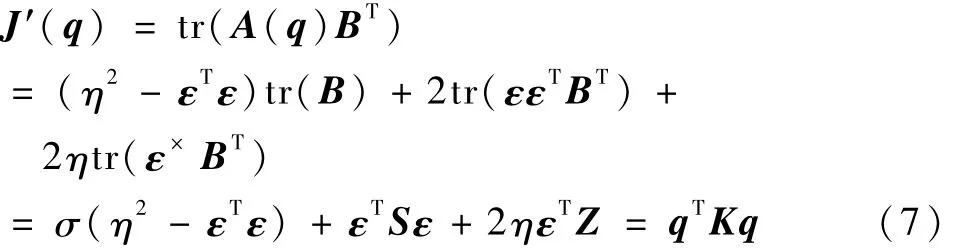
用拉格朗日法求增益函数J（q）的最大值，即

将上式求导，并使表达式等于0，得到Kqopt＝λmaxqopt，从而获得增益函数的表达式

通过上面公式的推导，最优姿态四元数就是矩阵K的最大特征值对应的特征向量.

2 QUEST算法与最小二乘算法的比较

2.1 恒星数目与计算精度之间的关系

下面计算中选择星表包含恒星数目为7085颗星的标准星表，视星等范围为－1.6～6.3；对整个天区进行的N＝20 000次随机采样，得出姿态计算误差，统计3σ范围内的误差标准差.

星敏感器的姿态计算精度对参与姿态计算的恒星数目和视场内星座的分布具有一定的敏感度.本节给出QUEST算法和最小二乘算法的计算精度与参与姿态计算的参考矢量数目之间的关系.

分析图1、图2得出以下结论：

（1）在参与姿态计算的恒星数目大于30时，QUEST算法与最小二乘算法的姿态计算精度都趋于稳定；

（2）当参与姿态计算的恒星数目较少，QUEST算法的计算精度要高于最小二乘算法.

2.2 姿态确定精度比较

比较内容：

（1）分别限定和不限定参与姿态计算的恒星数

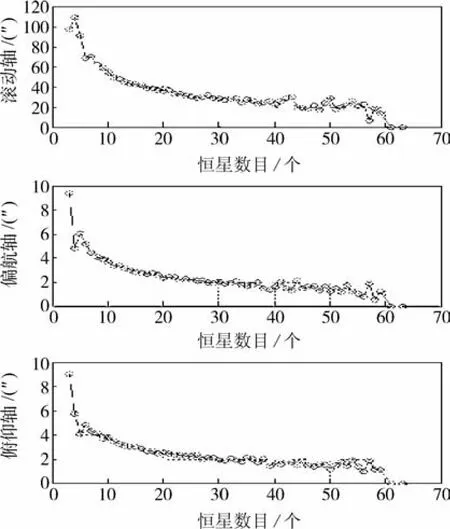
图1 QUEST算法恒星数目与姿态计算误差之间的关系

图2 最小二乘算法恒星数目与姿态计算误差之间的关系

目比较两种算法的计算精度；

（2）两种算法对应同一指向时计算精度与矩阵求逆条件数之间的关系.

仿真比较结果如表1所示.

在N＝20 000次运行结果中选择8处条件数差别较大的位置对两种算法进行比较，如图3所示.通过以上两部分的比较得出以下结论：

表1 各轴姿态角误差统计

图3 条件数与姿态测量误差间的关系

（1）当参与姿态计算的恒星数目较少时，QUEST算法具有较高的精度；

（2）对于任意天区，QUEST算法姿态计算精度要高于最小二乘算法.

由于计算过程中不存在对矩阵求逆的运算，所以QUEST算法对条件数不敏感，避免了线性方程的病态性对姿态计算结果的影响.

3 实例分析

构造三颗恒星在一条线上的特殊构型，使用QUEST算法和最小二乘算法分别进行姿态计算，比较两种算法在三星一线构型下的计算精.当星敏感器视场内出现三星一线构型时，使用最小二乘算法进行姿态计算，姿态计算误差出现如图4所示的跳变.对三星一线星图在星敏感器坐标系下绕其光轴进行任意角度（0°～360°之间）旋转，计算在该旋转角度下的三轴姿态误差.运行次数N＝1 000，对比QUEST算法、最小二乘计算的姿态计算精度.运行结果如表2所示.

图4 三星一线星图构型时最小二乘算法姿态计算误差出现波动

表格中失败次数是指各姿态确定算法在姿态计算之前首先判断是否满足各自的姿态计算条件，若不满足，则判为失败，该指向将不被用于姿态计算.

表2数据说明QUEST算法对不利构型具有强筛选功能，将不利构型完全剔除掉再进行姿态计算，保证了较高的姿态计算精度.

由图4可知，当星敏感器视场中恒星位置的相关性较大时，采用最小二乘算法计算所得的姿态测量误差非常大.这主要是因为最小二乘算法中采用了矩阵求逆的计算（公式2），当被识别的三颗导航星位置相关性较强的时候，（VTV）高度近似奇异，条件数最大高达cond＝2.38×107，求解姿态矩阵时线性方程的病态程度非常严重，（注：条件数cond＝‖VTV‖·‖（VTV）－1‖）.而QUEST算法通过对星图的筛选，将不利的星座构型全部剔除，从而保障了姿态计算的精度.结论如下：

（1）QUEST算法对于星图的选择条件相比最小二乘算法的正交条件筛选更为严格；

（2）结合第3部分，对于全天区星图，QUEST算法的精度优于最小二乘算法；针对三星一线这种特殊情况，QUEST算法仍然具有较高的精度.

表2 各种姿态确定算法精度比较

4 结 论

最小二乘算法QUEST算法都是在最小均方差意义下使损失函数最小而求得姿态矩阵.本文的比较结果表明，QUEST算法明显优于最小二乘算法，且QUEST算法对星图的筛选能力较强，从而防止了姿态计算出现错误的波动，保证了姿态计算的精度.因此，QUEST算法是一种比较优秀的姿态确定算法，值得学习和应用.

［1］ Markley F L，Mortari M.Quaternion attitude estimation using vector measurements［J］.The Journal of the Astronautical Sciences，2000，48（2／3）：359-380

［2］ Cheng Y，Shuster M D.Robustness and accuracy of the QUEST algorithm［C］.The 17thSpace Flight Mechanics Meeting，Sedona Arizona，Jan 2007

［3］ 陈希军.基于恒星敏感器的姿态确定算法研究［J］.控制工程，2008，15（3）：253-259

［4］ Shuster M D，Oh S D.Three-axis determination from vector observation［J］.Journal of Guidance and Control，1981，4（1）：70-77

［5］ Shuster M D.The quest for better attitudes［J］.The Journal of the Astronautical Sciences，2006，54（3）：657-683

Tradeoffs of Two Star-Tracker-Based Attitude Determination A lgorithms

SHIGuangqing，LU Xin，WU Yanpeng，HUANG Xin，WANG Li
（Beijing Institute of Control Engineering，Beijing 100190，China）

Two star-tracker-based attitude determination algorithms，the Least-Square（LS）algorithm and the quaternion estimator（QUEST）algorithm，are presented.This paper contains an accuracy comparison of the two algorithms under different observation vectors and any bore sight direction of the star tracker in the global area.The results show that the QUEST algorithm is more accurate than the LS one，even under the adverse constellation configuration.

star tracker；QUEST algorithm；Least-Square

V448.21

A

1674-1579（2009）05-0061-04

2009-04-07

史广青（1983—），女，山东人，硕士研究生，研究方向为光学敏感器（e-mail：shiguangqing999＠163.com）.