自由漂浮机械臂抓取翻滚目标的自适应控制策略*

王汉磊，解永春

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

自由漂浮机械臂抓取翻滚目标的自适应控制策略*

王汉磊1，，2解永春1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

提出了一种自由漂浮机械臂抓取翻滚目标的自适应控制策略.抓取翻滚目标要求自由漂浮机械臂具有很强的轨迹跟踪能力，但是自由漂浮机械臂本身以及目标所存在的运动学和动力学参数不确定性使基于模型的控制器性能急剧下降，甚至变得不稳定.通过对参数的自适应逐步改善基于模型的控制器的性能，并且提出了一种新的自由漂浮机械臂关节空间自适应控制器.最后通过数值仿真对所提出的自适应控制策略进行了验证.

自适应控制；不确定性；翻滚卫星；自由漂浮机械臂

近年来，在轨服务成为空间技术中的一个热点研究问题.翻滚目标卫星的捕获作为在轨服务中的一个典型操作任务，吸引了众多研究者的注意，并且越来越多的研究者建议采用机械臂完成对翻滚目标的捕获［1-3］.

利用空间机械臂捕获翻滚卫星主要可分为4个阶段［1］：1）接近、跟踪目标器的运动（抓取前动作：pre-grasping）；2）利用机械臂抓取目标器（接触：con-tact）；3）控制目标相对于追踪器的相对运动（抓取后的动作：post-grasping）；4）镇定组合体的翻滚运动（组合体镇定：compound stabilization）.空间机械臂的控制模式主要有3种：自由飞行、姿态受控和自由漂浮.自由漂浮模式所具有的潜在的优越性使其更加受到青睐.第一，不控制航天器的姿态和位置，可以节省不可更新的燃料，进而延长了系统使用寿命；第二，当服务卫星同目标卫星距离很近或发生接触时，自由漂浮控制模式可以避免姿态控制系统动作可能引起的碰撞.

在利用自由漂浮机械臂接近目标的过程中，要求机械臂末端具有很强的对目标的姿态位置跟踪能力.但是由于自由漂浮机械臂本身的动力学参数和运动学参数很难精确知道，因此基于模型的控制器无法满足控制性能要求.类似的，在机械臂抓住目标之后，空间机械臂系统的动力学参数和运动学参数会发生比较大的变化，这对控制系统提出了更加迫切的适应参数不确定性的要求.因此考虑采用自适应控制方法来改善基于模型的控制器的性能.在不同阶段具体采用的自适应控制律给出如下：

1）接近、跟踪目标器过程，采用文献［4］提出的自适应雅克比控制律.

2）在抓紧目标器之后，控制目标相对于追踪器的相对运动阶段采用关节空间自适应控制器，关节空间自适应控制器将在后文设计.

3）利用机械臂抓取目标器和镇定组合体的翻滚运动的过程不列入本文的研究内容，在此省略.

第一个自由漂浮机械臂自适应控制器出现于1993年［5］.该控制器被称为基于增广变量的自适应控制器.为避开自由漂浮机械臂经典形式的动力学模型无法线性参数化的困难，文中采用自由漂浮机械臂的增广模型设计控制器.但是这种控制方法的主要缺点是需要测量航天器的加速度信号，此外保证闭环系统稳定的条件也比较含糊.为了避免测量加速度，一些研究者提出采用神经网络［6－7］解决自由漂浮机械臂的自适应控制问题.利用自由漂浮机械臂系统的无源性，文献［3］提出了一种逆向链自适应控制方法，但文中没有对这种基于无源性的自适应控制器进行完整的稳定性分析，因此控制器在什么情况下是可行的问题没有得到回答.近年来的一些研究结果说明了考虑运动学参数不确定性的重要性［4］.文献［4］的研究结果也为本文提出的自适应控制策略的实现奠定了基础.

同在此之前的研究相比，本文的主要贡献有两个：第一，提出了一种利用自由漂浮机械臂抓取翻滚目标的自适应控制策略；第二，提出了一种不需要测量航天器加速度信号的自由漂浮机械臂关节空间自适应控制器，改善了自由漂浮机械臂操作大变动载荷的能力.

1 自由漂浮机械臂的动力学方程

显式包含航天器姿态运动的n自由度自由漂浮机械臂的动力学方程为［8］

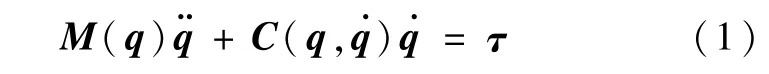
动力学方程（1）的几个基本特性列出如下.性质1.惯量矩阵M（q）一致正定，并且存在正常数α1，α2使得α1I≤M（q）≤α2I.

性质2.动力学方程（1）可表达为一组动力学参数ad＝（ad1，ad2…，adp）T的线性形式

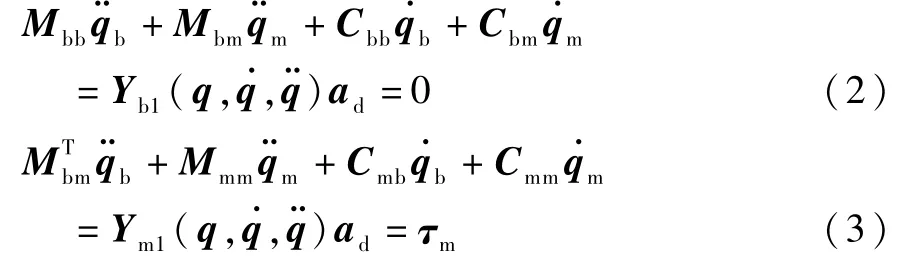
自由漂浮机械臂动力学的经典形式不显式包含航天器的姿态运动，且无法表达为一组动力学参数的线性形式.但是，动力学方程（1）显式包含航天器的姿态运动，文献［8］的研究结果表明，动力学方程

（1）确实可以表达为一组物理参数的线性形式.

2 关节空间自适应控制器设计及稳定性分析

本节基于自由漂浮机械臂的无源性设计自适应控制器.机械臂关节期望轨迹用qmd∈Rn表示和分别表示关节期望轨迹速度和加速度，并且假定和均有界.

基于无源性的控制方法的基本思想是通过改变系统的能量来实现控制目标，但是由于自由漂浮空间机械臂的控制输入的数目小于系统的自由度数，因此控制输入改变系统能量的能力是有限的，这在一定程度上增加了控制器设计的难度.此外，自由漂浮机械臂动力学的经典形式无法线性参数化.不过在此本文主要基于显式包含航天器姿态运动的动力学方程（1）设计控制器，以避开经典形式的动力学模型无法线性参数化的困难.

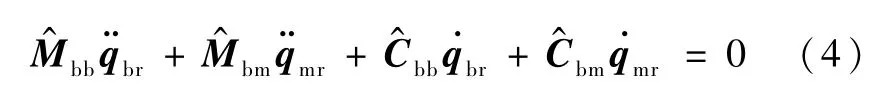
注1.引入航天器参考速度变量的意义在于，使用该变量可以避免测量航天器的姿态角加速度.因此提高了控制器的鲁棒性和抗干扰能力.定义航天器参考速度变量的思想来源于文献［4］.

定义一个航天器滑动模变量sb∈R3

那么

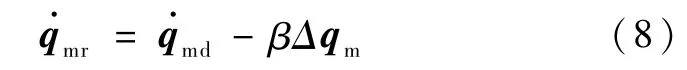
式中，β＞0为设计正常数，Δqm＝qm－qmd为关节位置跟踪误差.把方程（8）两边对时间求导，得到关节参考加速度

定义一个关节空间滑动模变量sm∈Rn

则

把方程（10）和（11）代入方程（3），得出

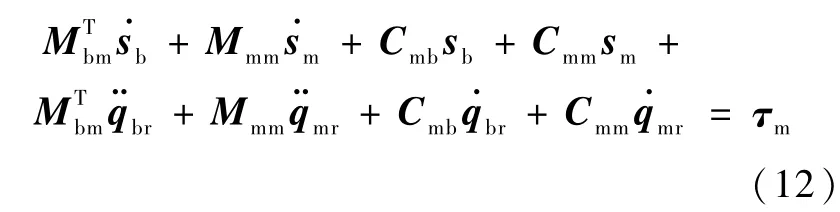
上述方程左边的最后4项可表达为一组动力学参数ad的线性形式

因此方程（12）可重写为

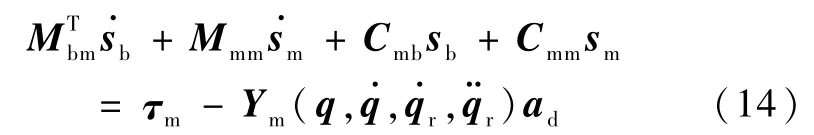
现在提出自适应控制律

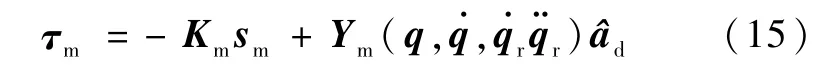
式中，Km∈Rn×n为对称正定反馈增益矩阵.动力学参数估计由下面的更新律更新：

式中，

把方程（4）代入动力学方程（2），得到闭环系统方程的第一部分式中，Δad＝＾ad－ad为动力学参数估计误差.

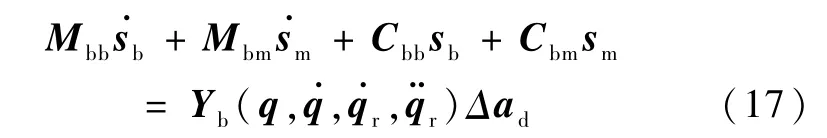
把方程（15）代入方程（14），得到闭环系统方程的第二部分

闭环系统方程（17）和（18）可写为更加紧凑的形式

用sT去乘方程（19）的两端，得出

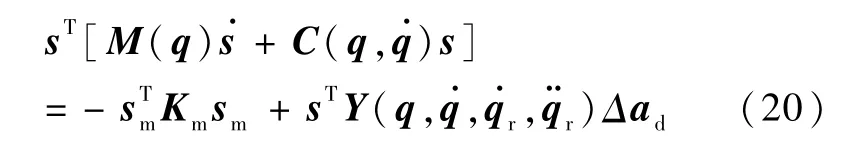
考虑Lyapunov-like备选函数把函数V对时间求导，得出

现在给出如下定理.

定理1.自由漂浮机械臂系统（1）在控制律（15）和参数自适应律（16）作用下，机械臂的关节轨迹跟踪误差渐近收敛于零.也就是说，当t→∞时，Δqm→0，

证明.由于≤0，因此s，Δad均有界.由方程（23），得出＋βΔqm∈L2，那么Δqm∈L2∩L∞，且当t→∞时，Δqm→0.由于Δqm有界，因此有界，进而有界.把方程（2）两边对时间积分，有Mbb＋Mbm＝C0，其中C0为自由漂浮机械臂系统的初始角动量，因此∈L∞.由s有界，可得∈L∞.由方程（9）知∈L∞.根据方程（4），有∈L∞.根据闭环系统方程（19），得到∈L∞，因此∈L∞.则一致连续，那么根据Barbalat定理［9］可以得到，当t→∞时

3 仿真实例研究

本节通过一个3自由度平面空间机械臂抓取翻滚目标的过程（图1所示）来说明所提出控制方案的可行性.3自由度平面空间机械臂的物理参数如表1和表2所示.

表1 航天器参数

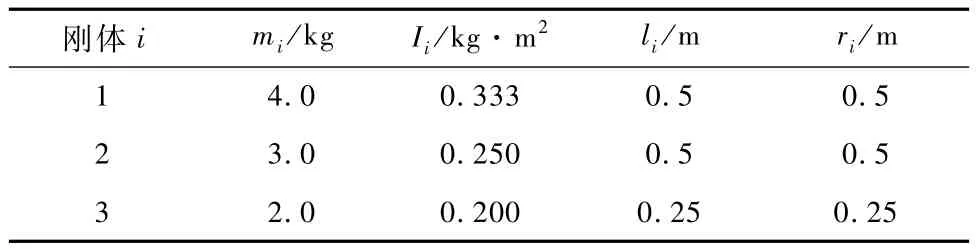
表2 机械臂参数

假定目标上存在一个合适的被抓机构（如图1所示），且抓取开始前目标处于翻滚状态，翻滚角速度ωt＝1.0 rad／s.在机械臂末端抓紧目标后，其末端同目标成为一个整体（即成为新的机械臂末端，图2）.目标的尺寸如图1所示.目标的物理参数为at＝1.0m（假定目标的边长均为at），质量为mt＝40 kg，转动惯量It＝7.0 kg·m2，目标器上的把手高度为h＝0.2m.

自由漂浮空间机械臂初始状态为：航天器质心位置RC0（0）＝[0 0]T，自由漂浮机械臂的初始构型取为qm（0）＝[π／3.0－2π／3.0π／3.0]T，航天器初始姿态qb（0）＝0，空间机械臂末端位置初值x(0)＝[2.0 0.0]T，空间机械臂的末端姿态初值θe(0)＝0.0.自由漂浮空间机械臂初始处于静止状态，亦即其初始线动量和角动量均为零.

目标质心位于图示正方形的几何形心，其在惯性系下的位置坐标为RCt(0)＝[2.8 0.0]T.

（1）接近、跟踪过程

在接近跟踪过程中，通过传感器获得目标的运动轨迹，在详细观察目标的运动之后确定合适的接近跟踪策略.接近过程中，机械臂末端首先沿着一个圆弧曲线运动至目标左下方RCt()0＋0.8×机械臂末端姿态调整至θe＝π／6.0（亦即指向目标器的质心），经历的时间为T.该圆曲线为

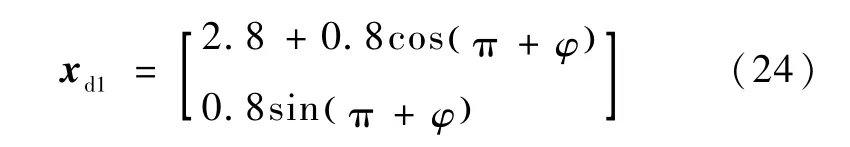
式中φ＝（3 t2／T2－2 t3／T3）×π／6.0，仿真中取T＝0.5 s.姿态期望轨迹为

在跟踪过程中，选择目标转动至θt（0）＝π／3.0时，开始控制自由漂浮机械臂跟踪目标上的被抓机构（handle）.机械臂末端位置的期望轨迹规划为

式中，

机械臂末端姿态的期望轨迹规划为θed2（t）＝π／6.0－ωtt.当t＝π／6.0 s，θt＝π／2.0时，xd2（t）与目标器的被抓机构（handle）位置重合，手爪姿态也同把手姿态对准，但是并不在此刻抓紧目标，而是让机械臂末端手爪跟踪目标器把手一段时间1－π／6.0 s之后再抓紧目标，也就说在经历了1.0 s之后，机械臂末端同目标器形成一个新的整体.

图1 自由漂浮机械臂抓取翻滚目标

图2 自由漂浮机械臂末端同翻滚目标联成一个整体

接近跟踪过程中，采用文献［4］提出的自适应雅克比控制器，与文献［4］不同的是此处采用复合参数自适应律，即在直接自适应控制律［4］的基础上加入预测误差，亦即采用复合参数自适应的思想［9］.复合参数更新律具有更好的跟踪性能，

式中，W＝λf／（p＋λf）Y1，λf＞0为滤波器参数，p为微分算子，e＝W＾ad－τf为滤波控制力矩预测误差，τf＝λf／（p＋λf）τ，ek＝为机械臂末端速度预测误差，Yk为运动学回归矩阵［4］.遗忘因子λ（t）＞0和λk（t）＞0为常值或者时变遗忘因子.增益P的初值选择为0＜P（0）≤K0，Pk的初值满足0＜Pk（0）≤K0k.其中，k0和k0k为两个对称正定矩阵，Rd和Rk为两个适当维数的对称正定矩阵.此处参数自适应增益P和Pk的更新律采用的是CF最小二乘更新律［10］.

控制器的参数取值确定为：Km＝100I，α＝10.0，P（0）＝10I，K0＝100I，Pk（0）＝0.1I，K0k＝10I，λ＝λk＝1.0，λf＝2.0，Rd＝1.0I，Rk＝100I.动力学参数估计的初值和运动学参数估计的初值分别确定为：

接近、跟踪过程的仿真结果如图3～图5所示.接近过程历时0.5 s，跟踪过程历时1.0 s，总过程历时1.5 s.图3为机械臂末端位置跟踪误差，图4为机械臂末端姿态跟踪误差.图5为机械臂末端的期望路径和实际路径.

图3 自由漂浮机械臂末端位置跟踪误差

图4 自由漂浮机械臂末端姿态跟踪误差

图5 机械臂末端位置期望路径和实际路径

（2）抓紧目标后控制目标相对于追踪器相对运动的过程

自由漂浮机械臂抓紧目标之后，末端同目标形成一个新的机械臂末端.新的机械臂末端使系统的动力学参数发生了巨大的变化，此外由于目标处于翻滚状态，则当机械臂抓紧目标之后，目标的角动量也传递给了自由漂浮机械臂系统.为了能够实现对目标的停靠，首先需要镇定新的机械臂末端（含有目标）同追踪器（自由漂浮基座）之间的相对运动，以为后面的组合体姿态镇定做好准备.

在没有明确的相对停靠要求的情况下，可以采用自由漂浮机械臂关节空间自适应控制器镇定目标相对于基座的相对运动.镇定的目标确定为，在时间t＝T＝2 s后，qm（T）＝［π／3.0－2π／3.0π／3.0］T，˙qm（T）＝0.关节轨迹以三次曲线运动规律规划，即三个关节的运动参数φ1，φ2，φ3分别采用三次曲线运动规律

本文要求机械臂的关节在T时间后处于静止状态，即关节速度为零，因此φi满足，φi（0）＝0，φi（T）＝qmi（T）－qmi（0），φ′i（0）＝0，φ′i（T）＝0.根据这4个条件可求出φi()t的显式表达式.这样可以得到自由漂浮机械臂的关节期望轨迹

式中Φ（t）＝［φ1（t）φ2（t）φ3（t）］T.

本文采用控制器（15）来控制自由漂浮机械臂的关节运动，参数更新采用复合自适应的思想［9］，即在方程（16）基础上加入预测误差

关节空间自适应控制器控制参数取为：Km＝100I，β＝10.0，P（0）＝50I，K0＝100I，λ＝1.0，λf＝2.0，Rd＝1.0I.动力学参数估计的初值确定为（0）＝100.0T.

图6 关节位置跟踪误差

控制目标相对于基座相对运动过程的仿真结果如图6～图9.图6为关节位置跟踪误差曲线.图7为各关节的期望轨迹和实际轨迹，图8为关节速度曲线.从图中看出，关节速度最终趋于零，亦即达到了镇定目标器与自由漂浮基座之间的相对运动的目的.图9为PD控制（τm＝－Kmsm）作用下的关节位置跟踪误差，对比图6可以得出，自适应控制器显著改善了系统的跟踪性能.

图7 关节期望轨迹和实际轨迹

图8 关节速度曲线

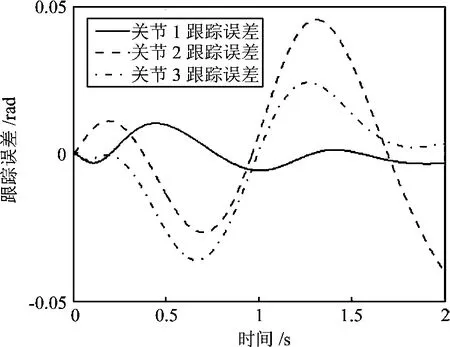
图9 PD控制作用下的关节位置跟踪误差

4 结 论

本文提出了一种自由漂浮机械臂抓取翻滚目标的自适应控制策略.自由漂浮机械臂以及目标存在的参数不确定性使基于模型的控制器性能急剧下降，甚至变得不稳定.因此，通过参数自适应逐步改善基于模型的控制器的性能.此外为了改善抓取翻滚目标之后的自由漂浮机械臂关节空间轨迹跟踪性能，本文提出了一种新的自适应控制器.该控制器通过引入一个航天器参考速度矢量，避免测量航天器的加速度.最后通过数值仿真考查了所提出的自适应控制策略的性能.

［1］ Abiko S，Hirzinger G.On-line parameter adaptation for a momentum control in post-grasping of a tumbling target with model uncertainty［C］.IEEE International Conference on Intelligent Robots and Systems，CA，USA，Oct 29-Nov 2，2007

［2］ Rekleitis I，Martin E，Rouleau G，et al.Autonomous capture of a tumbling satellite［J］.Journal of Field Robotics，2007，24（4）：275-296

［3］ Abiko S，Hirzinger G.An adaptive control for a freefloating space robot by using inverted chain approach［C］.The IEEE／RSJ International Conference on Intelligent Robots and Systems，California，USA，Oct 29-Nov 2，2007

［4］ Wang H，Xie Y.Passivity based adaptive Jacobian tracking for free-floating space manipulators without using spacecraft acceleration［J］.Automatica，2009，45（6）：1510-1517

［5］ Gu Y L，Xu Y.A normal form augmentation approach to adaptive control of space robot systems［C］.IEEE Conference on Robotics and Automation，Atlanta，GA，May 1993

［6］ Sanner R M，Vance E E.Adaptive control of free-floating space robots using“neural”networks［C］.The American Control Conference，Seattle，Washington，June 1995

［7］ Taveira T F P，Siqueira A A G，Terra M H.Adaptive nonlinear H∞controllers app lied to a free-floating space manipulator［C］.IEEE International Conference on Control Applications，Munich，Germany，Oct 4-6，2006

［8］ Xu Y，Shum H Y，Lee J J，et al.Adaptive control of space robot system with an attitude controlled base［C］.IEEE International Conference on Robotics and Automation，Nice，France，May 1992

［9］ Slotine J J E，Li W.Applied nonlinear control［M］.Englewood Cliffs，NJ：Prentice-Hall，1991

［10］ LiW，Slotine JJE.An indirect adaptive robot controller［J］.Systems＆Control Letters，1989（12）：259-266

Adaptive Control Scheme for the Capture of a Tumbling Spacecraft Using Free-Floating Space Manipulators

WANG Hanlei1，2，XIE Yongchun1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

In this paper，we have proposed an adaptive control scheme for the capture of a tumbling spacecraft using free-floating space manipulators.Capturing tumbling target spacecraft requires the freefloating spacemanipulator to have high tracking performance.However，uncertainties always exist in both the free-floating space manipulator and the target spacecraft.In the presence of parameter uncertainties，model based controllers tend to give deteriorated performance or even become unstable.Thus，we employ parameter adaptations to improve the performance ofmodel based controllers，and we have also proposed a novel joint-space adaptive controller for free-floating spacemanipulators.Simulation results are presented to show the performance of the proposed adaptive control scheme.

adaptive control；uncertainty；tumbling spacecraft；free-floating manipulator

*国家自然科学基金（90305024）资助项目.

2008-11-05

王汉磊（1982—），男，山东人，博士研究生，研究方向为机器人自适应控制（e-mail：wanghanlei0 l＠yahoo.com.cn）.

TP273

A

1674-1579（2009）05-0006-07