高超声速飞行器离散模糊自适应控制*

高道祥，孙增圻，3

（1.清华大学计算机科学与技术系智能技术与系统国家重点实验室，北京100084；2.清华信息科学与技术国家实验室，北京100084；3.空间智能控制技术国家级重点实验室，北京100190）

高超声速飞行器离散模糊自适应控制*

高道祥1，2，孙增圻1，2，3

（1.清华大学计算机科学与技术系智能技术与系统国家重点实验室，北京100084；2.清华信息科学与技术国家实验室，北京100084；3.空间智能控制技术国家级重点实验室，北京100190）

根据高超声速飞行器的欧拉近似离散模型，提出基于Back-stepping的模糊离散自适应控制器设计方法.结合模糊自适应控制和反馈线性化的方法，Back-stepping设计的每一步虚拟／实际控制量对系统非匹配的不确定性都能进行较好地补偿.稳定性分析表明，该控制方法能够保证系统跟踪误差和模糊自适应参数误差是一致终值有界的.仿真使用了高超声速飞行器的纵向模型对算法进行了验证，得到了满意的控制效果.

高超声速飞行器；模糊控制；离散控制；飞行控制

在高超声速飞行中，大范围变化的飞行环境和由于飞行动力学实验数据的缺乏而导致的动力学参数的不确定性是高超声速控制系统设计面临的主要问题.高超声速飞行器的动力学方程具有高度非线性、不稳定、多变量耦合以及气动参数不确定等特点.因此，依赖于相对精确数学模型的传统控制器设计方法很难应用于高超声速飞行器的控制器设计中去.要适应大范围的飞行环境和高机动性要求，控制系统就必须具有高可靠性、鲁棒性、强适应性和强抗干扰能力［1］.

另外，目前的高超声速飞行器的控制方法大都是针对飞行器的连续系统模型设计连续控制器，如基于微分几何理论的输入输出线性化控制［2－4］，轨迹线性化控制［5］和Back-stepping［6］控制等.而基于Back-stepping的自适应控制策略是传统飞行控制乃至一类复杂非线性系统控制比较有效的方法.文献［7］用神经网络为战斗机的飞行控制设计了Backstepping自适应重构系统.文献［8-9］研究了非线性系统中Back-stepping的设计方法，分别采用模糊自适应控制和神经网络自适应控制方法补偿系统未知的不确定性.

但随着计算机技术的发展，未来高超声速飞行器的控制任务大部分都需要由计算机实现，因此，需要考虑高超声速飞行器离散控制器的设计方法，即，采样控制器的设计.一般地，很难获得连续非线性系统的精确离散模型，因此，通常选取非线性系统的离散近似模型进行控制器设计，如文献［10］根据机器人的近似离散模型，研究了机器人的动态神经网络采样自适应控制方法.文献［11］提出了基于对象特征模型描述的智能自适应的采样控制方法，这些方法在仿真和实际应用中都取得了较好的控制效果.

本文根据高超声速飞行器纵向运动模型的特点，通过简化，得到高超声速飞行器的具有严格反馈形式非线性模型，然后采用欧拉近似法转化为离散系统，根据近似离散系统模型设计离散控制器，由于严格反馈非线性系统的欧拉近似模型［12］不改变系统的严格反馈形式，因此，适合于Back-stepping离散控制器的设计.对于系统模型中不确定性和控制器设计过程中的非因果问题，采用模糊自适应系统进行在线补偿，离散闭环系统的渐近稳定性通过Lyapunov理论进行了证明，仿真说明算法在速度和高度的控制中具有较好跟踪性和鲁棒性.

1 高超声速飞行器的模型描述

高超声速飞行器是具有六自由度的复杂非线性系统，本文只考虑其纵向运动的Back-stepping控制器设计，高超声速飞行器通用的纵向模型［2］如下：

发动机动态模型采用二阶系统模型

式中，βc为控制器的输出控制指令.为得到高超声速飞行器模型的严反馈形式，作如下假设.

假设1.式（3）中的推力项T sinα远远小于升力项L，可认为T sinα≈0.由于航迹倾角γ较小，取sinγ≈γ.根据飞行器航迹倾角γ，攻角α和俯仰角θp的定义有，θp＝α＋γ.定义x＝［x1，x2，x3，x4］T，x1＝h，x2＝γ，x3＝θp，x4＝q，u＝δE，根据假设，高超声速飞行器的模型可以改写为如下的一般非线性形式：

假设2.fV（V，x2，x3，x4，β）、f2（V，x2）、f4（V，x2，x3，x4）、g2（V）和g4（V）为光滑函数，存在常数gi1≥gi0＞0，使gi1≥gi（·）≥gi0＞0，i＝2，4.

设采样时间为T，通过欧拉近似法将式（7）离散化

式中，系统的控制量β（t）＝β（kT）＝：β（k），u（t）＝u（kT）＝：u（k），∀t∈［kT，（k＋1）T］为分段光滑的函数，状态变量V（k）＝：V（kT），xi（k）＝：xi（kT）在采样时刻可测.

注意到离散系统（8）仍为一严格反馈系统，适合采用Back-stepping方法设计控制器，并且，假设2对g2（V（k））和g4（V（k））同样适用.

假设3.高超声速飞行器的飞行速度变化较慢，且变化范围较小，即在有限的采样周期内，V（t＋kT）≈V（t）.

注1.由式（7）可知，高超声速飞行器动力学系统包含两个子系统，即由节流阀β控制的速度子系统和由舵偏角δE控制的高度子系统，控制的目标是使V→Vd，h→hd，Vd，hd为给定的速度指令和高度指令.本文将两个子系统控制器分开设计，对高度子系统，采用Back-stepping设计方法.对于速度子系统，采用反馈线性化的控制方法，使飞行器速度保持在期望值附近.

2 离散控制器设计

2.1 Back-stepping高度控制器

Back-stepping［13］控制为一类含有非匹配不确定性的非线性系统提供了有效的控制器设计方法，这种方法通过递推设计过程将一个复杂的非线性系统分解为系列的低阶系统，然后选取一个状态变量为虚拟控制量，通过为每个低阶子系统选取适当的Lyapunov函数，设计最终的实际控制量达到控制目标.控制器设计过程如下：

1）定义误差z1（k）＝x1（k）－x1d（k），式中，x1d（k）＝hd（k）为给定的高度指令，假设其提前四步的期望值可得，根据式（8），有

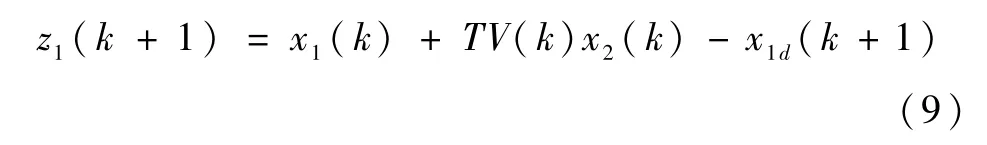
由于x1（k）-子系统不存在不确定性，将x2（k）作为x1（k）-子系统的虚拟控制量，则有

式中，0＜c1＜1.定义z2（k）＝x2（k）－x2d（k），将式（10）代入式（9）可得

2）由定义z2（k）＝x2（k）－x2d（k），x2（k）-子系统可为

式中，x2d（k＋1）为虚拟控制量x2d（k）的未来值，在实际计算中无法获得，称为离散系统Back-stepping设计中的“非因果性”问题.根据式（8）和假设3，x2d（k＋1）可看作V（k），x1（k），x2（k），x1d（k），x1d（k＋1），x1d（k＋2）的未知函数，另外，f2（V（k），x2（k）），g2（V（k））为不确定函数，因此，式（12）中的集总不确定函数可表示为

式中，f2N（V（k），x2（k））和g2N（V（k））分别为函数f2（V（k），x2（k））和g2（V（k））的标称值，h2（k）可采用模糊系统，神经网络，B样条函数等具有“万能逼近”性能的函数进行逼近，本文采用模糊系统对h2（k）进行在线估计，即，

则可使模糊系统对x2（k）-子系统的不确定性和x2d（k＋1）进行整体逼近.

应用式（13）和式（14），式（12）可改写为

选取x3（k）为x2（k）-子系统的虚拟控制量，可得

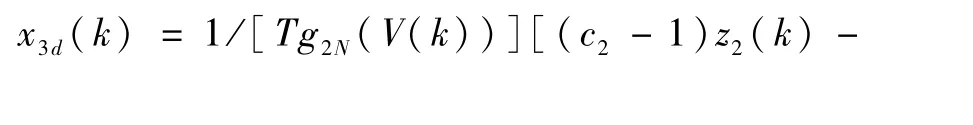
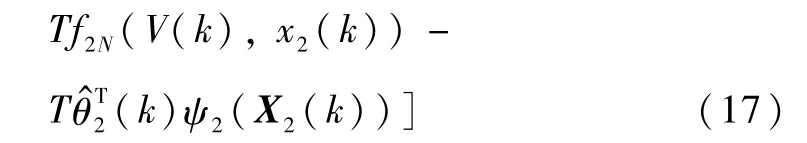
式中，0＜c2＜1为常数，设计如下自适应律在线估计

式中，δ2＞0；λ2＞0为常数.将式（17）代入式（12），并定义z3（k）＝x3（k）－x3d（k）得

3）考虑x3（k）-子系统，由z3（k）＝x3（k）－x3d（k）可得

x3（k）-子系统不包含不确定函数，但x3d（k＋1）未知，则函数

需采用模糊系统进行辨识

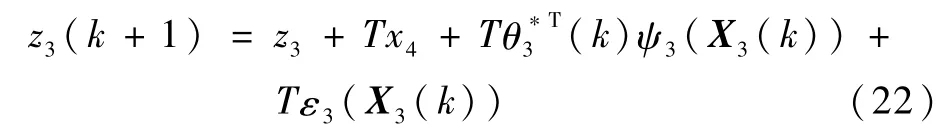
将x4（k）看作x3（k）-子系统的虚拟控制量

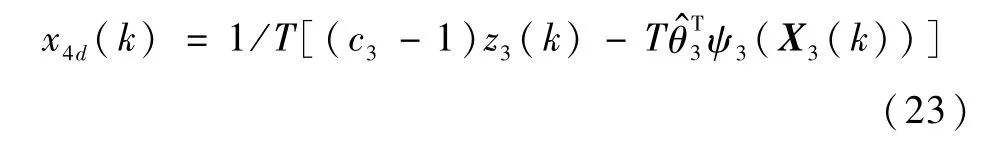
式中，0＜c3＜1为常数.自适应律为

式中，δ3＞0；λ3＞0为常数.定义z4（k）＝x4（k）－x4d（k），根据式（23），式（20）可改写为

4）这是Back-stepping设计的最后一步，可根据1～3步，设计系统的实际控制量.考虑x4（k）-子系统和z4（k）＝x4（k）－x4d（k），

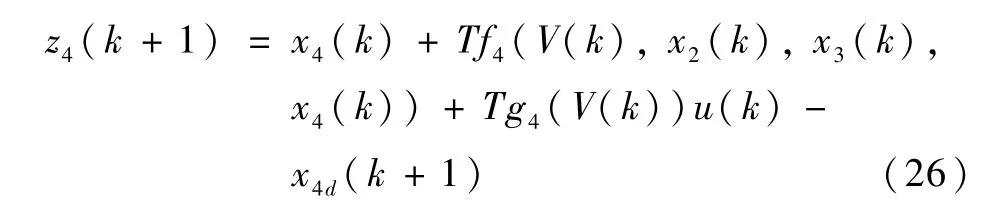
考虑系统的不确定函数f4（V（k），x2（k），x3（k），x4（k）），g4（V（k）），x4d（k＋1），则采用模糊系统辨识如下函数：

式中，f4N（V（k），x2（k），x3（k））和g4N（V（k））分别为函数f4（V（k），x2（k），x3（k））和g4（V（k））的标称值，则实际控制量为

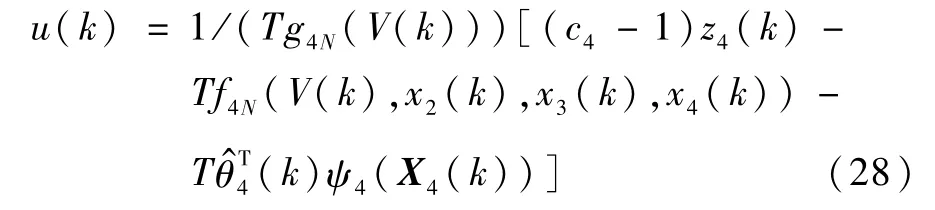
式中，0＜c4＜1为常数.将式（28）代入式（26）可得

自适应律为

式中，δ4＞0；λ4＞0为常数.

2.2 稳定性分析

本节采用离散Lyapunov理论进行高超声速飞行器离散控制系统的稳定性分析.选取Lyapunov函数为

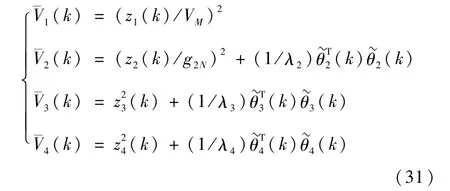
式中，VM＞V（k）为一常数，模糊自适应参数的误差动态方程为

根据不等式2ab≤ρa2＋（1／ρ）b2（ρ＞0为适当常数）和式（11），（19），（25），（29），（32），分别计算式（33）的各项为

式中，

式中，

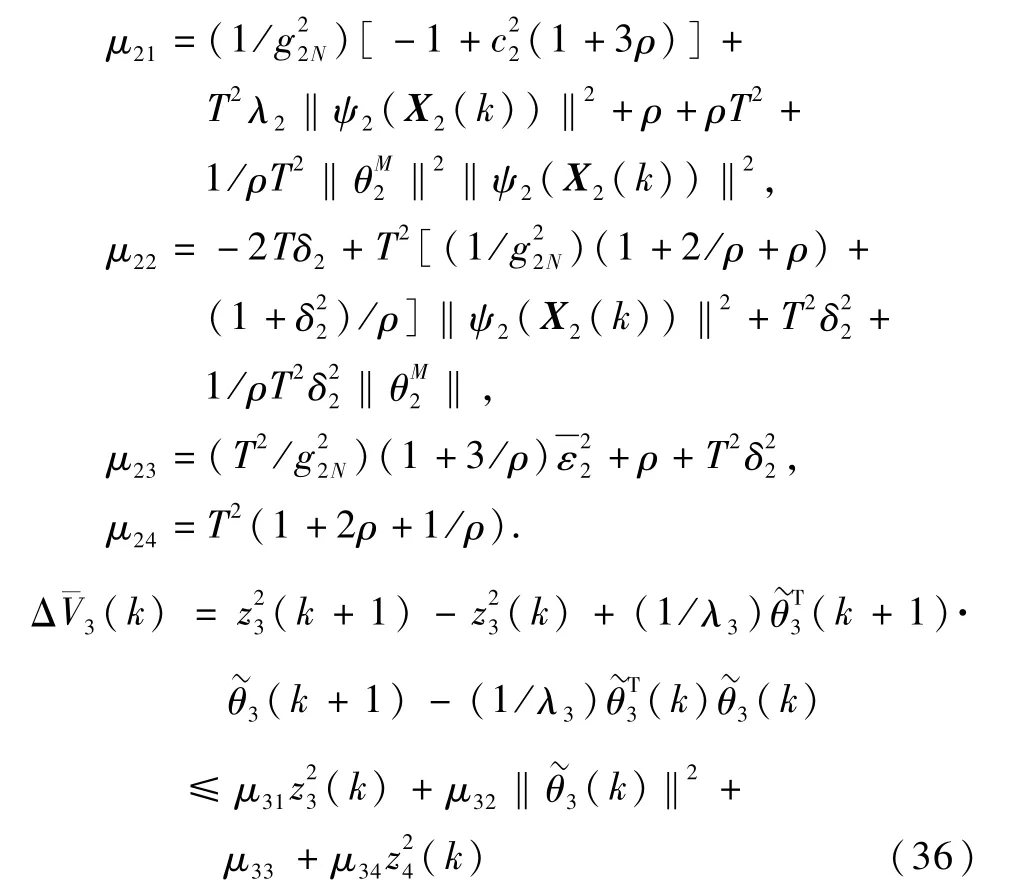
式中，

式中，

结合式（34）～（37），可得

式中，选择适当的ci、δj、λj和ρ，i＝1，…，4，j＝2，3，4，使

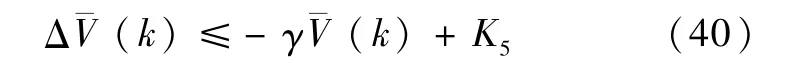
可推导得

定理1.对于高超声速飞行器离散系统（8），采用控制器（10），（17），（23）和（28），如果选择ci，i＝1，…，4，δj，λj，j＝2，3，4，满足条件（39），则离散闭环系统的误差是一致终值有界的.

注2.ψi（Xi（k）），i＝2，3，4为模糊基函数，由其定义可知，‖ψi（Xi（k））‖N为模糊规则数.式（34）～（37）的各项中大都包含T或T2的乘积项，由于采样时间T较小，因此容易选择适当的ci，i＝1，…，4，δj，λj，j＝2，3，4，保证闭环控制系统的稳定性，虽然1／ρ较大，但T／ρ可保证为较小常数.

2.3 速度控制器设计

考虑式（8）中的速度子系统可改写为如下的仿射非线性系统：

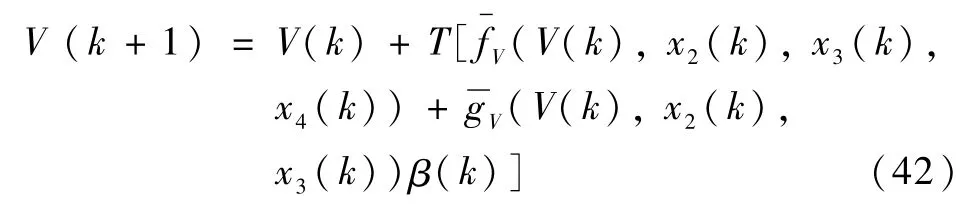
设期望轨迹为Vd（k＋1），Vd（k），令zV（k）＝V（k）－Vd（k），采用反馈线性化方法设计离散控制器为

式中，gVN（V（k），x2（k），x3（k）），fVN（V（k），x2（k），x3（k），x4（k））为不确定函数的标称值，与假设2相似，存在gV0，gV1＞0，使gV0＜＜gV1.自适应律设计为

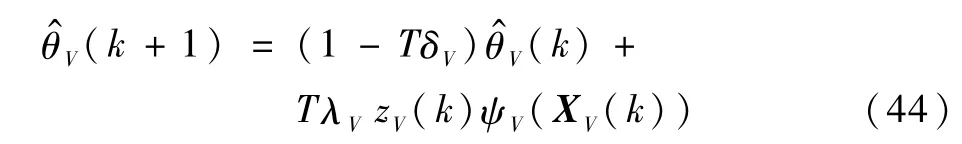
式中，δ4，λ4＞0，采用上述同样的方法，容易证明系统的稳定性.

3 仿真分析

对高超声速飞行器在高度h0＝33 528m，速度为V＝4 590.3m／s巡航条件下的飞行情况进行仿真研究，飞行器仿真模型为连续非线性系统，其参数见文献［2］.控制的目标是要求飞行器跟踪给定的高度指令和速度指令.本文给出了以下情况的仿真结果.

1）高度阶跃hc＝610m，速度V＝4 590.3m／s.

2）速度阶跃Vc＝30.5m／s，高度h＝335 28m.

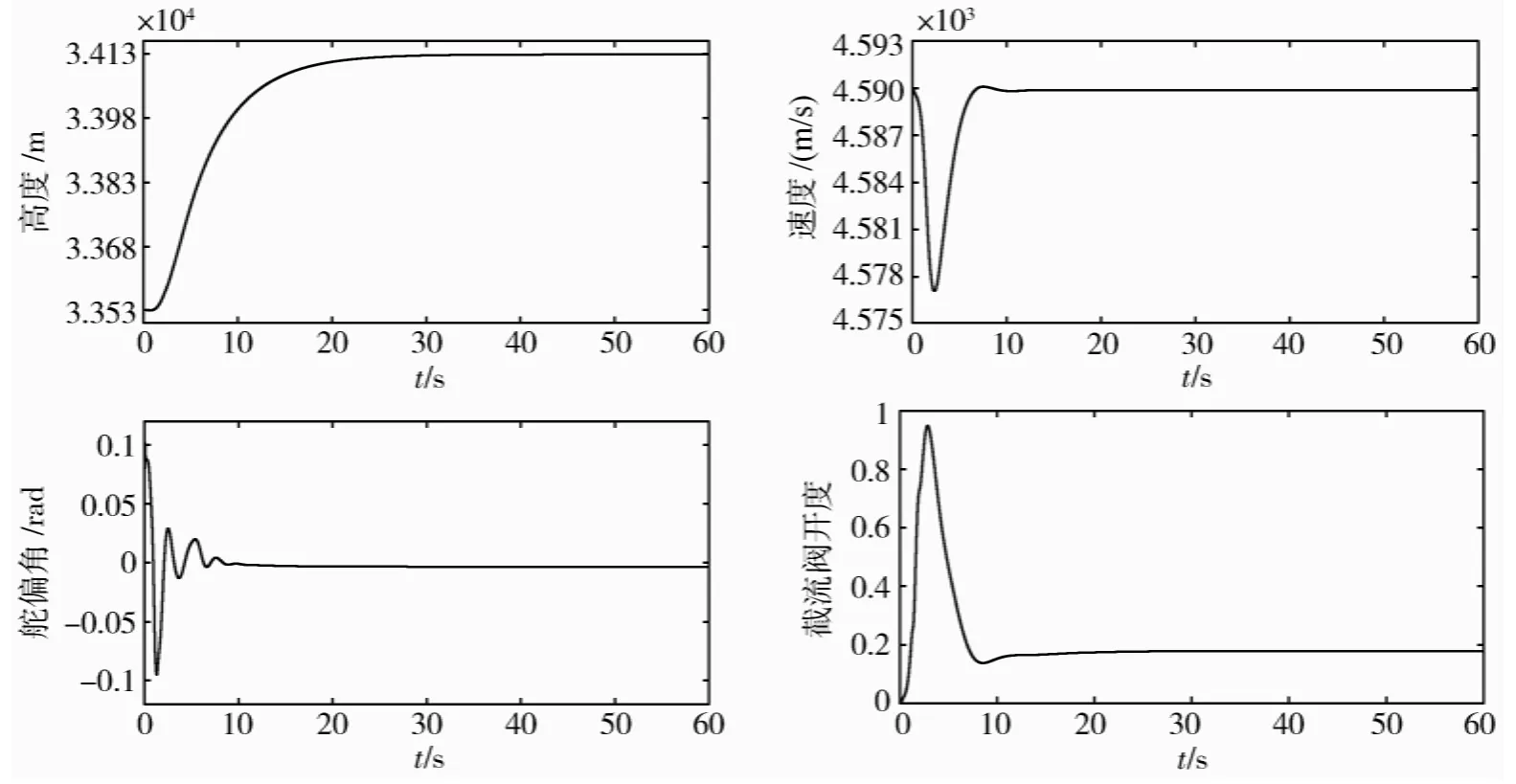
图1 高度阶跃变化（33528m～34138m）的仿真结果

3）高度变化为幅值610 m，周期80 s的方波信号，速度V＝4 590.3m／s.选取如下线性系统作为指令参考模型，hd／hc＝（ωn1）／［（s＋ωn1）（s2＋2ζωn2s＋）］，Vd／Vc＝ωn1／（s＋ωn1），式中，ωn1＝0.2 rad／s，ωn2＝1 rad／s，ζ＝0.7，s为Lap lace算子.模糊系统的隶属度函数为

图2 速度阶跃变化（4590.3m／s～4620.8m／s）的仿真结果

图3 高度周期变化的仿真结果

4 结 论

本文根据高超声速飞行器欧拉近似离散模型，采用Back-stepping方法进行离散控制器的设计，对于飞行器中存在的不确定参数，设计了离散模糊自适应系统进行在线补偿，并对离散系统的稳定性进行了理论分析，证明了离散闭环系统的误差是一致终值有界的.最后对飞行器进行了高度和速度指令跟踪的仿真研究，得到了较为理想的控制效果.

［1］ 吴宏鑫，胡军，解永春.空天飞行器智能自主控制若干问题［C］.国家自然科学基金“空天飞行器的若干重大基础问题”重大研究计划年度交流会，北京，2005

［2］ Wang Q，Stengel R F.Robust nonlinear control of a hypersonic aircraft［J］.Journal of Guidance，Control and Dynamics，2000，23（4）：577-584

［3］ Xu H J，Ioannou P A，Mirmirani M.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance，Control and Dynam ics，2004，27（5）：829-838

［4］ Xu H J，Mirmirani M，Ioannou P A.Robust neural adaptive control of a hypersonic aircraft［C］.AIAA Guidance，Navigation，and Control Conference and Exhibit，Austinm，Texas，Aug 11-14，2003

［5］ 张春雨，方炜，姜长生.基于T-S模糊系统的空天飞行器鲁棒自适应轨迹线性化控制［J］.航空学报，2007，28（5）：1153-1161

［6］ Gao D X，Sun Z Q，Du T R，Dynamic surface control for hypersonic aircraft using fuzzy logic system［C］.IEEE International Conference on Automation and Logistic，Jinan，Aug 2007

［7］ Shin D H，Kim Y D.Reconfigurable flight control system design using adaptive neural networks［J］.IEEE Transactions on Control Systems Technology，2004，12（1）：87-100

［8］ Li Y H，Qiang S，Zhuang X Y，Kaynak O.Robust and adaptive backstepping control for nonlinear systemsusing RBF neural networks［J］.IEEE Transactions on Neural Networks，2004，15（3）：693-701

［9］ Zhang T，Ge S S，Hang C C.Adaptive neural network control for strict-feedback nonlinear systems using backstepping design［J］.Automatica，2000，36（12）：1835-1646

［10］ Sun F C，Li H X，Li L.Robot discrete adaptive control based on dynam ic-inversion using dynamical neural networks［J］.Automatica，2002，38（11）：1977-1983

［11］ 吴宏鑫，刘一武，刘忠汉，等.特征建模与挠性结构的控制［J］.中国科学（E辑），2001，31（2）：137-149

［12］ Mareels IM Y，Penfold H B，Evans R J.Controlling nonlinear time-varying systems via Euler approximations［J］.Automatica，1992，28（4）：681-696

［13］ Kokotovic P V.The joy of feedback：nonlinear and adaptive［J］.IEEE Control System Magazine，1992，12（7）：7-17

Discrete-Time Fuzzy Adaptive Control for the Hypersonic Aircraft

GAO Daoxiang1，2，SUN Zengqi1，2，3
（1.State Key Laboratory of Intelligent Technology and System，Department of Computer Science and Technology，Tsinghua University，Beijing 100084，China；2.Tsinghua National Laboratory for Information Science and Technology，Beijing 100084，China；3.National Laboratory of Space Intelligent Control，Beijing 100190，China）

A fuzzy discrete adaptive controlmethod via back-stepping design is proposed for the hypersonic aircraft by using its Euler approximation discrete model.By combining the fuzzy adaptive control and feedback linearization，themismatched uncertainties can be well compensated by designing a corresponding virtual／actual control input in each back-stepping design procedure.Stability analysis shows that the proposed scheme can guarantee the uniform ultimate boundness of the system tracking errors and fuzzy weight estimation errors.The longitudinalmodel of a hypersonic aircraft is used to demonstrate the effectiveness of the proposed strategy.

hypersonic vehicle；fuzzy control；discrete control；flight control

*国家自然科学基金（90405017，90716021，60604010，60736023）、空间智能控制技术国家级重点实验室基金及开放基金项目（SIC07010202），中国博士后科学基金（20070410528）资助项目.

2008-11-29

高道祥（1972—），男，博士后，山东人，主要研究方向为航天器智能自主控制（e-mail：dausson＠163.com）.

V4

A

1674-1579（2009）05-0013-07