基于GTLS的零动量卫星惯量矩阵在轨辨识
2009-12-12林佳伟
林佳伟,王 平
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
基于GTLS的零动量卫星惯量矩阵在轨辨识
林佳伟1,2,王 平1
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
使用广义总体最小二乘(GTLS,generalized total least squares)方法对零动量卫星进行惯量矩阵在轨辨识.提出了GTLS算法的先验最小距离解的定义:当测量信息不足以确定唯一解时,解空间中最接近先验估计的解.给出了先验最小距离解的算法,并应用于惯量矩阵在轨辨识.仿真结果表明了该辨识方法的有效性及先验最小距离解相对于最小范数解的优越性.
零动量卫星;惯量矩阵;在轨辨识;广义总体最小二乘;先验估计
惯量矩阵参数是卫星力学模型的重要参数,当前的工程实践中卫星的惯量矩阵参数是由卫星结构分析得到的.通过对卫星结构进行建模,预先估计帆板展开、推进剂消耗等引起的卫星的结构变化,从而获得惯量矩阵参数的先验估计.但是在卫星的实际运行中预先估计可能发生偏差,例如:推进剂余量难以准确估计,液体在失重状态下漂浮不定,太阳翼和天线等大型附件的展开不能为结构模型所完全描述,从而使先验估计偏离真值.以卡西尼卫星为例,“干”星的惯量矩阵的不确定性为±10%[1-2].通过在轨辨识,可以获得比先验估计更准确的惯量矩阵信息,建立准确的力学模型,并为控制器提供准确的参数,从而提高控制系统的性能.
当前国际上对惯量矩阵的辨识方法存在如下缺点:没有采用完整的动力学方程;未考虑测量噪声;未能保证估计的一致性[3].文献[1]提出了基于总体最小二乘(TLS,total least squares)的惯量矩阵在轨辨识方法,可以克服这些缺点.本文使用GTLS方法对该方法进行扩展,适用于更一般的模型,并具有更好的数值稳定性.考虑到工程实际中对机动次数的限制可能导致测量信息不足,因此本文对GTLS算法进行了改进,以便于利用先验信息.
1 估计方程
假设整个星体相对于惯性空间的总角动量(包括卫星主体角动量和存储在星上动量装置的角动量)在初始时刻为0.没有外力矩的作用时,根据动量守恒原理,在本体坐标系中有

式中,h为存储在星上动量装置的角动量,J为卫星惯量矩阵,ω为卫星主体角速度.
使用星上动量轮驱动机构将h控制到某一个值,然后用动量轮转速测量机构测量h,同时用陀螺测量ω.由于测量噪声的存在,方程组等号不成立,即h+Jω≈0.为了抑制噪声的影响,得到更好的估计,进行多次机动以获得多组方程(一般而言为超定的非一致方程组).
将方程转化为ωTJ=-hT.以惯量矩阵J作为待估计参数X,进行m次机动,相应的方程组为

从方程可以看出,要确定唯一的解,要求卫星3轴都安装动量装置.另外还应预先估计整星相对于惯性空间的总角动量,推力器喷气将整星角动量调为0.
当前工程中的动量轮转速测量常使用测频率的方法,即通过测量一定时间内的转角脉冲数来测量轮子的平均转速,由于每一组机动结束后h的值不变,所以延长测量时间可以提高测量精度.同理也可以得到较高精度的角速度测量值.
2 求解算法
2.1 用GTLS算法进行惯量矩阵参数估计
考虑矩阵A∈Rm×n中有一些列是精确已知的情
形,即A=[A1A2],A1∈Rm×n1是不受噪声污染的已知量,A2∈Rm×n2受到噪声污染.未受扰方程为

而A20和B0的量测值为

式中:下标0表示未受噪声污染的真值;待估计参数的真值X0∈Rn×d,X10∈Rn1×d,X20∈Rn2×d;量测值A2和B的真值分别为A20和B0,受到加性噪声ΔA2和ΔB的污染;矩阵[ΔA2ΔB]均值为0,其各行向量之间独立同分布,记其协方差阵C进行Cholesky变换得C=GTG;假定A1和A20列满秩.
可见此时方程是广义误差变量回归(GEIV,generalized errors-in-variable)模型[4].GTLS方法是针对GEIV模型的求解方法,要求满足如下准则[4]:
准则1.寻找和使得range⊆range,并且最小.
其中,‖‖F指Frobenius范数(简称为F范数),range(·)指的是矩阵的值域,range⊆range等价于有解.
文献[4]中给出了GTLS算法,可用来求解X.具体步骤如下.
1)若n1=n,则退化为最小二乘方法;否则对[A1A2B]进行QR分解得

其中,Q为正交阵,R11∈Rn1×n1为上三角阵,R22∈R(m-n1)×(n2+d).若n1=0,则把[A]B赋给R22.
2)若协方差阵C给定且与单位阵不成比例(即不等于单位阵乘上某个标量),则进行Cholesky分解,得C=GTG;若C与单位阵成比例,则退化为TLS算法.
3)对矩阵对R22和G进行广义奇异值分解,得

4)确定矩阵对R22和G的秩p.它可以由未受扰方程的性质确定,也可以选取一个很小的数R0,若σ1≥…≥σp>R0≥σp+1≥…≥σn2+d,则认为σp+1≈…≈σn2+d≈0.
5)将[zp+1…zn2+d]赋给Z2,其中zi为Z的列向量,下标表示列数.再由R11Z1=-R12Z2计算Z1.
6)若d>1且p<n2,通过QR分解,使交化,得=QzRz,并将Qz赋给;否则进入下一步.
8)若Γ非奇异,则GTLS有解,对方程^XΓ=-Y进行求解可得^X;否则应减小p的值再重新计算,将p-ρ赋给p,其中ρ是σp的重数.
2.2 对算法的讨论
GTLS方法在两方面扩展了TLS方法:
1)经典的TLS方法只能应用于行误差向量的协方差阵为单位阵的情形,而GTLS方法扩展到了一般矩阵.
2)GTLS方法可以处理测量系数矩阵A中的一些列不含误差的情形.
当n1=0且G与单位阵成比例时,GTLS算法退化为经典TLS算法,可见文献[1]所提方法是本方法的特例.当n1=0但G与单位阵不成比例时,GTLS算法理论上等价于对方程进行缩放变换后的TLS算法,此时估计具有一致性[1].由于GTLS算法采用了广义奇异值分解,避开了对G直接求逆,当协方差阵为病态矩阵时可以提高数值稳定性.而当n1≠0,即A中有一些列精确已知时,无法使用TLS方法求解.
3 先验最小距离解
有时候测量信息不足以给出唯一解,此时GTLS算法的步骤4)中接近0的奇异值的个数大于3.当机动次数不够、机动设计不好(例如几次机动完全相同)、动量装置自由度小于3时,都可能出现这种情况.
2.1节中的原始GTLS算法在解空间中取出最小范数解,其物理意义不清楚,可能与真值区别很大.为了提高估计精度,考虑利用先验信息得到更接近真值的估计.在此定义先验最小距离解:当GTLS方法存在多解时,在其解空间中寻找一个与先验估计距离最小的解.在这里用两个解之差的F范数描述它们的距离.与最小范数解相比,先验最小距离解具有明确的物理意义,一般而言更接近真值.本节中先给出求解算法,然后证明算法求出的解与先验估计的距离最小.
3.1 讨论前提与符号表示
对[A B]G-1进行奇异值分解,再对矩阵对[A B]和G进行广义奇异值分解,两组奇异值相同[6].
在本节中,仅考虑n1=0的情形,即所有列都包含误差.2.1节步骤3)中,当n1=0时,R22=[A B],对矩阵对[A B]和G进行广义奇异值分解的符号与对矩阵对R22和G进行广义奇异值分解的符号相同.
对[A B]G-1进行奇异值分解,得[A B]G-1=UΣVT.其中U和V为[A B]G-1的左右奇异矩阵,分块成V=[V1V2]=,U=[U1U2].V1和U1的列数为p,V11∈Rn×p,V22∈Rd×(n-p+d).考虑具有多重广义奇异值σp+1=…=σn+d的情形,并且p<n.当m≥n+d时,Σ=其中Σ1=diag{σ1,σ2,…,σp}∈Rp×p,Σ2=diag{σp+1,…,σn+d}=σp+1In+d-p,In+d-p表示单位阵,下标为维数.记与σp+1,…,σn+d相对应的右奇异向量为νp+1,…,νn+d.
3.2 先验最小距离解的求解算法
记X的先验估计为Xp,当矩阵对[A B]和G有多重广义奇异值σp+1=…=σn+d时,对[zp+1…zn+d]进行列变换得

式中,M是列初等变换阵,Y∈Rn×(n-p),Id为d维单位阵.
选取N1∈R(n-p)×d,使得‖Xp-S-YN1‖F取最小,这是一个最小二乘问题.
本小节只列出算法,下面证明所得的S+YN1是解空间中与先验估计的距离最小的解.
3.3 先验最小解的证明
定理1.满足GTLS准则1的‖[AG-1‖F的最小值为σn+d.
证明.根据矩阵低秩逼近的Eckart-Young-Mirsky定理[7]:其中σ为E的奇异值,其下标按大小排列.若方程有解,则rankG-1}≤n.由[A B]-当σn+1=…=σn+d时,
定理2.存在一个满秩矩阵K,使得G[zp+1…zn+d]K=[νp+1…νn+d].
证明.根据奇异值分解的性质[6-7],[νp+1…νn+d]和G[zp+1…zn+d]的列向量都是相对于[A B]G-1的多重特征值的特征向量.νp+1,…,νn+d互相正交,是特征向量空间的正交基,而G[zp+1…zn+d]列满秩,也是特征向量空间的一组基.所以K是特征向量空间中两组基的转换阵,它是满秩的.
定理3.{S+YN|∀N∈R(n-p)×d}是GTLS问题的解集,对于某一个给定的N,相应的

其中d维方阵R由K-1M进行QR分解而得,即K-1M=QR,Q的各列向量为单位正交向量组.
证明.首先证明G-1的F范数为最小.

由K-1M=QR得G-1[νp+1…νn+d]Q,将其代入的表达式得=σp+1U2QQT[νp+1…νn+d]T

第3个等号是由于V的各列向量为单位正交向量组而得的.
[νp+1…νn+d]T[νp+1…νn+d]、QTQ、都为单位阵,得
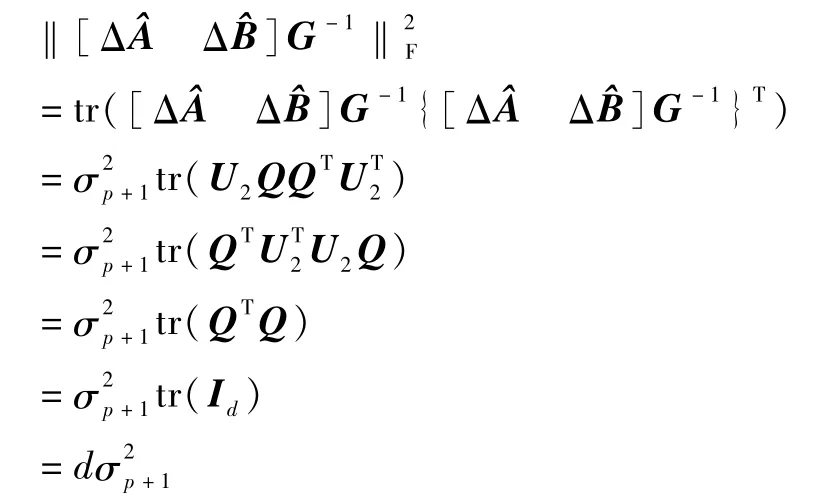

所以,YN+S是^AX=^B的解,即∀N∈R(n-p)×d,S+YN都存在一个相对应的[Δ^AΔ^B],满足2.1节的准则1.
定理4.S+YN1是GTLS解集中的先验最小距离解.
证明.定理3中指出{S+YN|∀N∈R(n-p)×d}是GTLS问题的解集,而在3.2节的算法中,N1使‖Xp-S-YN1‖F取最小,即S+YN1是解空间中与先验估计Xp距离最小的解.
3.4 讨 论
若要求解先验最小距离解,并不需要对Z进行归一化(2.1节的步骤3).这是因为归一化相当于对其右乘一个满秩矩阵,而从证明过程中可以看出,这么做并不影响解集的表达式.
一般认为奇异值的个数为min{m,n+d},当m<n+d时,对[A B]G-1的奇异值分解UΣVT进行扩维得[U 0]VT,其中Σ2=diag{σp+1,…,σn+d},新增加的σm+1,…,σn+d为0,它们对应的左奇异向量为0.由于本文中只讨论σp+1=…=σn+d的情形,此时Σ2=0,对应测量信息不足的情形.代入证明过程中,结论依然成立.
实际上,无论是TLS算法还是GTLS算法,都可以看成是结构总体最小二乘(STLS,structured total least squares)算法的特殊情形[8-10].但是STLS方法一般情况下只有数值近似解法,无法保证求出指标函数的全局最小点,而TLS和GTLS算法由于模型的特殊性,可以求出使指标函数全局最小的解,从而保证了估计的一致性.由结构总体最小二乘算法的性质可知[9],在高斯噪声的条件下,GTLS是GEIV模型的极大似然估计.极大似然估计在渐近意义上能接近方差下界,有时被认为是最优的估计,这就是选择GTLS方法的原因.
4 仿真算例
首先验证基于GTLS的惯量矩阵参数估计方法的有效性.惯量矩阵参数的真值为kg·m2.仿真条件为:角速度测量误差的均值为0,标准差为0.003(°)/s;卫星本体坐标系3轴的3个动量轮中,有两个可以获得精确的测量值,第3个动量轮的转速测量包含高斯噪声,噪声均值为0,标准差为0.3 rad/min.3轴上的动量轮装置的容量的上限为10 kg·m2/s.仿真1×103次,根据仿真结果计算估计误差阵的F范数的均值.仿真结果如表1所示.

表1 估计误差阵的F范数的均值
从表1中可以看出,随着测量次数不断增大,估计误差越来越小.
当机动次数m为64时,进行1×104次仿真,得到估计结果的均值,它与真值的差为可以看出估计的均值与真值十分接近.
可见,仿真结果表明了基于GTLS的惯量矩阵参数估计方法的有效性.
下面比较最小范数解与先验最小距离解.将先验估计看成是真值加上一个加性噪声矩阵,所有矩阵元素都是互不相关的零均值高斯噪声,均方误差为200 kg·m2.假设只进行两次机动,所有测量都包含误差,噪声条件不变.
仿真1×104次,先验估计、最小范数解、先验最小距离解的误差阵的F范数的均值分别为584.6、2 952.3和341.2这3种估计的均值与真值的差分别为

从仿真所得的估计误差阵的F范数和均值可以看出,先验最小距离解要优于先验估计和最小范数解.
5 结 论
本文使用GTLS方法进行零动量卫星的惯量矩阵在轨辨识,提出了GTLS算法的先验最小距离解的定义和算法,并将其应用在惯量矩阵辨识中.与文献[1]提出的基于TLS的惯量矩阵在轨辨识方法相比,本文提出的方法适用于更一般的模型,具有更强的数值稳定性.文中对GTLS算法进行了改进,当测量信息不足时在解空间中取出与先验估计距离最小的解,相对于文献[4]所提的最小范数解,先验最小距离解充分利用了先验估计信息,有利于提高估计精度.在工程实际中经常使用动量轮对卫星进行单次的姿态机动,其测量信息不足以确定唯一的惯量矩阵参数,此时可以应用先验最小距离解.
本文的研究对象是零动量卫星,采用了简单的刚体模型,并且没有考虑外界干扰.在后续的研究工作中应考虑放松这些限制,扩大本方法的应用范围.
[1] Lee A Y,Wertz JA.In-flight estimation of the Cassini spacecraft’s inertia tensor[J].Journal of Spacecraft and Rockets,2002,39(1):153-155
[2] Wertz J,Lee A Y.In-flight estimation of the Cassini spacecraft’s inertia tensor[C].The 11thAAS/AIAA Space Flight Mechanics Meeting,Santa Barbara,California,Feb 11-15,2001
[3] 林佳伟,王平.零动量卫星惯量矩阵的在轨辨识[C].中国航天可持续发展高峰论坛暨中国宇航学会第三届学术年会,北京,2008
[4] Van Huffel S,Vandewalle J.Analysis and properties of the generalized total least squares problem AX≈B when some or all columns in A are subject to error[J].SIAM J.Matrix Anal,1989,10(3):294-315
[5] Van Huffel S,Vandewalle J.The total least squares problem:computational aspects and analysis[M].Philadelphia:SIAM,1991
[6] Golub G H,Van Loan C F.Matrix computations[M].3 rd ed.Baltimore,Maryland:The John Hopkins University Press,1996
[7] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004
[8] Lemmerling P.Structured total least squares:analysis,algorithms and applications[D].Department of Electrical Engineering,Katholieke Universiteit,Leuven,Begium,1999
[9] Abatzoglou T,Mendel J,Harada G.The constrained total least squares technique and its application to harmonic superresolution[J].IEEE Trans.Signal Process,1991,39(5):1070-1087
[10] De Moor B.Total least squares for affinely structured matrices and the noisy realization problem[J].IEEE Trans.Signal Process,1994,42(11):3104-3113
In-Orbit Identification of the Inertial Matrix of Zero Momentum Satellite
LIN Jiawei1,2,WANG Ping1
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.National Laboratory of Space Intelligent Control,Beijing 100190,China)
A generalized total least squaresmethod is adopted to in-orbit identification of the inertialmatrix of a zero momentum satellite.A prior minimum distance solution is defined:this solution closest to the prior estimate in solution space as ifmeasurement information is not enough to determine a unique solution.An algorithm of the priorminimum distance solution is proposed,and applied to in-orbit identification of an inertialmatrix.Simulation results validate feasibility of the identification method and advantage of the priorminimum distance solution over the minimum norm solution.
zero momentum satellite;inertial matrix;in-orbit identification;generalized total least squares;prior estimation
2009-05-28
林佳伟(1982—),男,福建人,博士研究生,研究方向为航天器在轨辨识(e-mail:linjw0207@gmail.com).

V448.22
A
1674-1579(2009)05-0026-05
