利用GPS接收机的精确轨道确定技术

2009-12-12孙宝祥

空间控制技术与应用 2009年5期

关键词：天球根数航天器

孙宝祥

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

利用GPS接收机的精确轨道确定技术

孙宝祥1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

利用GPS接收机的导航信息精确确定接收机载体航天器的轨道根数.给出了为确保10 m量级的定轨精度所必需的精确坐标系变换与时间系统变换公式，提出了采用GPS接收机的导航信息与摄动运动方程式外推的组合导航方法，以保证接收机天线被短期遮挡时导航仍能正常运行.

轨道确定；轨道根数；导航信息

GPS定位结果为WGS-84（world geodetic system 1984）协议地球坐标系中的三维位置、三维速度及时间，卫星轨道是以J2000.0协议天球坐标系为参考系的.本文的研究内容是如何利用GPS接收机的导航信息精确确定接收机载体航天器的轨道根数.为确保10 m量级定轨精度，本文给出了必需进行的精确坐标系变换与时间系统变换公式.提出了采用GPS接收机的导航信息与摄动运动方程式外推的组合导航方法，以保证接收机天线短期被遮挡时航天器导航仍能正常进行.

1 坐标系和时间系统

1.1 坐标系

航天器轨道坐标系源于基本天文参考系.瞬时地球坐标系是以历元t的瞬时地极Pt定义的，其坐标原点在地球质心，Zt轴指向瞬时地极Pt（真地极），Xt轴指向瞬时地极和ECTP（协议赤道与起始子午线的交点）构成的格林尼治平起始子午线与真赤道的交点E，Yt轴与Xt、Zt轴构成右手坐标系［1］.

WGS-84协议地球坐标系与瞬时地球坐标系的差别主要来自协议地极与瞬时地极之间的差别.协议地极CTS也称国际协议原点CIO.瞬时地球坐标系也称准地固坐标系，协议地球坐标系也称地固坐标系.

天球坐标系是以地球质心为原点，以天轴为基准轴，以春分点定义的坐标系.天轴实际即地球自转轴，由于地球的形体接近一个赤道隆起的椭球体，因此在日月引力和其他天体引力对地球隆起部分的作用下，地球在绕太阳运行时，自旋轴方向不再保持不变，而是在空间绕北黄极产生缓慢的旋转，因而使春分点在黄道上产生缓慢的西移，由于地球自转轴在惯性空间进动所造成的这种现象称为岁差.

北天极在天球上绕北黄极旋转的轨迹不是平滑的小圆运动，而是沿着类似圆的波浪曲线向西运动.也就是说，在岁差圆周运动上叠加了振幅很小的短周期分量，这种现象称为章动.

仅考虑岁差影响的北天极称为瞬时平北天极，与其相应的天球赤道和春分点，称为瞬时天球平赤道和瞬时平春分点.以瞬时平北天极和瞬时平春分点为基准的天球坐标系称为瞬时平天球坐标系，也称瞬时平赤道地心系.

实时观测的北天极（即包含了岁差与章动的北天极）称为瞬时北天极（或称真天极），而与之相应的天球赤道和春分点称为瞬时天球赤道和瞬时春分点（或称真天球赤道和真春分点）.以瞬时北天极和瞬时春分点为基准建立的天球坐标系，称为瞬时天球坐标系，也称瞬时真赤道地心系.

J2000.0协议天球坐标系，其原点位于地球质心，Z轴向北指向J2000.0平赤道的极点，X轴指向J2000.0平春分点，所以J2000.0协议天球坐标系即2000年1月1日12：00标准历元的瞬时平天球坐标系，也称J2000.0地心惯性系.

J2000.0协议天球坐标系与瞬时平天球坐标系之间的转换与岁差有关.设瞬时平天球坐标系中的三维位置矢量为，J2000.0协议天球坐标系中对应的三维位置矢量为rCIS＝（X Y与rCIS的转换关系为：

式中，（PR）为岁差矩阵，由三个旋转矩阵构成，即

式中，Ri（θ）为绕i轴转θ角的旋转矩阵（i＝x，y，z），三个赤道岁差参数ζA、ZA、θA的计算公式为［2－3］

T为从历元J2000.0＝2000年1月1.5日TDB（太阳系质心力学时）＝JD2451545.0 TDB起算至观测历元t的儒略（Julian）世纪，即

瞬时平天球坐标系与瞬时天球坐标系之间的转换与章动有关.设瞬时天球坐标系中的三维位置矢量为与rM的转换关系为

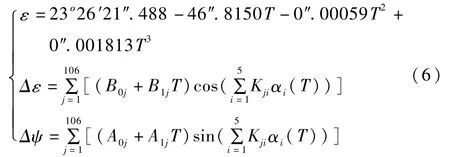
Δε、Δψ包括周期从4.7天到6 798.4天（18.6年）且振幅大于0″.0001的共106项，可只取最大的前5项，国际天文联合会给出了IAU1980章动序列前五项对应的及

5个基本变量α1～α5分别是月球的平近点角I、太阳的平近点角I′、月球平升交角距F、日月平角距D和月球轨道升交点平黄经Ω，可以忽略其与T3有关的章动项.

瞬时天球坐标系与瞬时地球坐标系的Z轴均指向瞬时地球自转轴的极点，故两者指向相同；X轴指向不同，瞬时天球坐标系指向真春分点，瞬时地球坐标系指向格林尼治平均子午面与赤道的交点，两者的夹角为格林尼治真恒星时GAST.

真恒星时是真春分点的时角，对应于格林尼治子午圈世界时0h的真恒星时为：

式中，赤经章动等于黄经章动在赤道上的分量.赤经章动和黄经章动同样分长周期项和短周期项，长周期项变化在±1s.2之间，短周期项变化在±0s.02之间，赤经章动在一天内变化不大，可以略去.GMST0为世界时0h的格林尼治平恒星时，世界时M的格林尼治真恒星时为

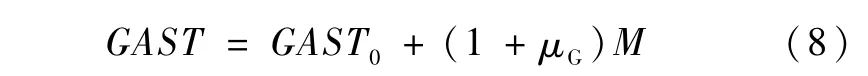
式中，μG＝0.002 737 909 3，μGM为平太阳时转换为恒星时所增加的改正项.

设瞬时地球坐标系中的三维位置矢量为rDt＝则瞬时天球坐标系与瞬时地球坐标系的转换关系为：

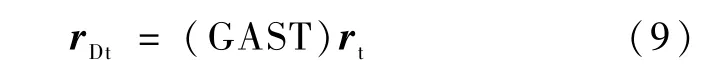
式中，（GAST）为以小时为单位的格林尼治真恒星时GAST换算成角度所对应的转换矩阵，即

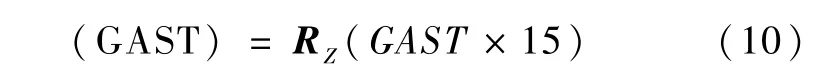
需要注意的是，世界时0时相对于2000年1月1日12h（JD＝2 451 545.0）起算的儒略日JD（t）取值为±0.5，±1.5，±2.5….

瞬时地球坐标系与协议地球坐标系的转换与地轴极移有关，地轴极移是地球自转轴在其本体内的移动.地轴在没有外力作用下产生的极移称自由极移，周期为432天，振幅约为0″.2；外部作用力引起的周年运动称受迫极移，振幅约0″.1.地轴极移还包括由地球液核引起的周期约1日的近周日自由极移和由日月引力引起的周日受迫极移，还有地极的长期运动和周期长达二三十年的长周期运动.协议地球坐标系的Z轴指向平极（协议地极CTP）.

瞬时地球坐标系对应的瞬时极相对于协议地球坐标系的平极的直角坐标记作（xP，yP），由平极指向格林尼治子午线方向为X轴的正向.

设协议地球坐标系中的三维位置矢量为rCTS＝则协议地球坐标系与瞬时地球坐标系的转换关系为：

式中极移矩阵（EP）＝Ry（－xP）Rx（－yP），极移量xP、yP由国际时间局所属台站的观测资料推算，由国际地球自转服务机构（IERS）提供.

协议天球坐标系与协议地球坐标系的转换关系为

1.2 时间系统

时间要素包括计量起点和单位时间长度，从1984年开始，天文年历中太阳、月球和大行星各基本历表的时间改用力学时，以代替以前使用的历书时，轨道计算涉及的时间系统包括：恒星时（ST）、世界时（UT）、质心动力学时（TDB）和原子时（TAI），简述如下［3－7］.

春分点连续两次过中天的时间间隔称“恒星日”，真恒星时是子午圈距真春分点的时角，地球上每一个地方子午圈的地方真恒星时GASTλ等于格林尼治真恒星时GAST加子午圈经度.

平恒星时是平春分点与子午圈所夹的时角，平恒星时加上赤经章动即真恒星时.

世界时以1／86400平太阳日为秒长，格林尼治平太阳时称为世界时UT0，平太阳时起始点在子夜（即太阳下中天），它是天文观测直接测定的，对应瞬时极的子午圈.UT0加上极移Δλ改正后的世界时称UT1，UT1加上地球自转速度的季节性变化的改正ΔTS后的世界时称UT2.

1967年第十三届国际度量衡会议引入新的秒长定义，即铯原子基态的两能级间跃迁辐射的9192631770周为1秒长，称为国际制秒（SI秒），由这种时间单位确定的时间系统称为国际原子时（TAI），国际原子时时刻的起算点取为1958年1月1日0hUT，两者起算偏差为－0s.0039.

由于世界时有长期变慢的趋势，世界时时刻将日益落后于原子时，为了避免发播的原子时与世界时产生过大偏离，1972年起国际上发播时号多用协调世界时（UTC），其时间单位为原子秒长，其时刻与UT1的偏离保持不超过0.9 s，方法是在年中或年底进行跳秒，即每次调整1 s.

轨道计算时应有两个时间，即北京时和协调世界时UTC，而内部计算时采用世界时UTC，输出量的时间加上8h，化成北京时.

GPS时（GPST）属于原子时系统，其秒长与原子时秒长相同，计算原点规定在1980年1月6日0时，与UTC时刻一致，以后即按照原子秒长累积计时，不进行跳秒调整.GPST与UTC之间的差距会逐渐加大，并将一直是秒的整数倍，与TAI在任一瞬时都有19 s常量差.

而GPST与UTC的关系及其常值差可在导航电文中获得，美国国家海洋电子协会规定的NMEA-0183标准中GPS接收机输出的导航结果采用UTC时间.

2 由导航结果确定用户星的密切轨道根数［1，2，5，8］

2.1 密切轨道根数

以轨道根数为基本变量的摄动运动方程是拉格朗日（J-L.Lagrange）在1808年首先提出来的，故又称拉格朗日摄动方程.若用户星绕地球的运行可用开普勒二体运动来描述，则卫星沿一椭圆轨道运行，任何瞬时由卫星的位置矢量r和速度矢量可以唯一地确定一组六个轨道根数，对于开普勒轨道，只要参考历元时间不变，六个轨道根数均是常数（平近点角随参考历元时间而变，其余五个参数不随时间变化）.实际上卫星还受到地球非球形摄动，大气阻力摄动，日、月摄动，太阳光压摄动等各种较小的干扰，卫星进行姿态控制时小推力器工作的反作用力对卫星的轨道运动也有影响，所以卫星实际上是沿着一条复杂的曲线运动的，这曲线不一定在一个平面内，也不一定封闭.但为研究方便，将卫星实际轨道上的每一点看成是某相应椭圆轨道上的点，这种椭圆轨道称为密切轨道，卫星在该点的实际速度等于密切轨道上相应点的速度，即实际轨道与密切轨道相切，密切轨道是连续变化的椭圆轨道，密切轨道根数不再是常数，是时间的函数.密切轨道根数也称轨道瞬时根数.

2.2 用户星的密切轨道根数的确定

如前所述，GPS接收机导航的结果是用户星在瞬时WGS-84地球坐标系中的三维位置、三维速度，则J2000.0协议天球坐标系中的用户星位置矢量和速度矢量为

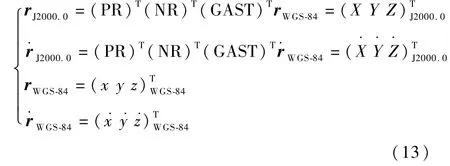
为简便起见，下面省略下标J2000.0，根据开普勒方程可得轨道半长轴a、偏心率e、偏近点角E、平近点角M和真近点角f.

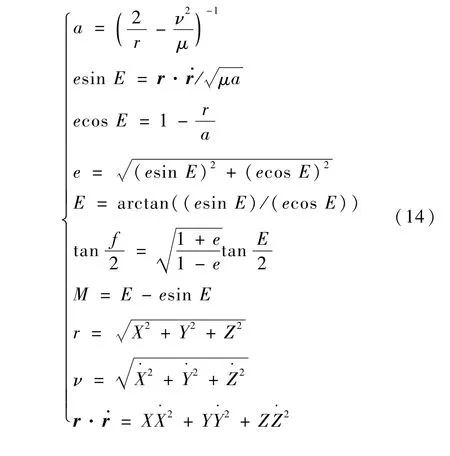
由卫星动量矩h可导出轨道倾角i、升交点赤经Ω

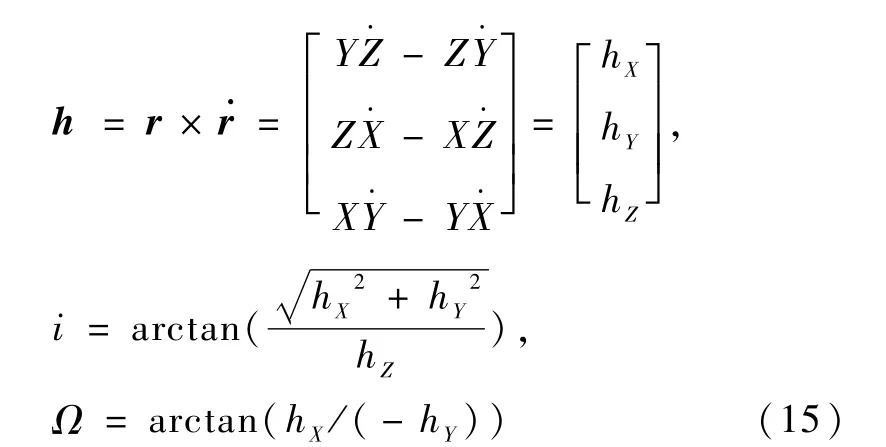
Ω、E、M与f取值范围为0°～360°，中低轨道卫星和飞船的轨道倾角通常为40°～100°，因此式中i的反正切函数取值范围为0°＜i＜180°.

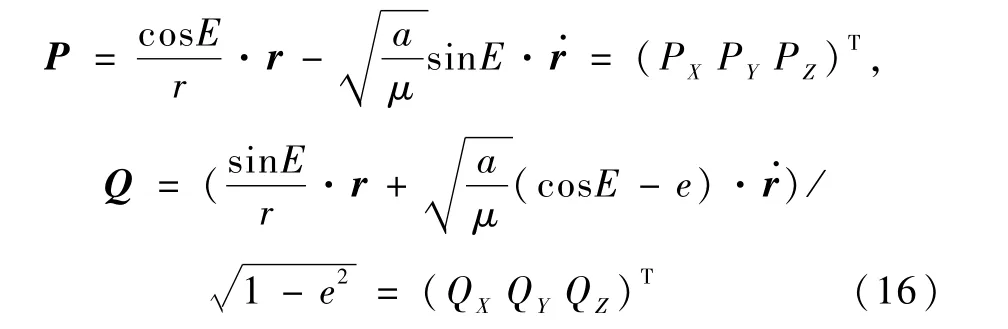
由P、Q可求得近地点幅角ω：

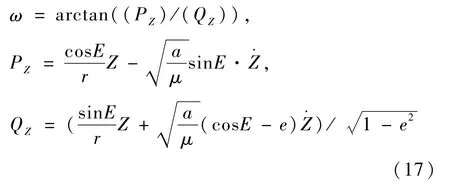
式中ω与E、Ω类似，取值范围为0°～360°.考虑到轨道根数a＞0，0≤e＜1，在e＝0的特殊情况下，用开普勒方程不能求得偏近点角E的值，但仍可由P、Q的关系式求得.e＝0时，真近点角f、偏近点角E、平近点角M均相同.

3 轨道摄动运动方程［1，2，5，8］

3.1 以轨道根数为基本变量的摄动运动方程

不论是保守力还是非保守力，都可用摄动加速度分量的形式建立相应的轨道摄动运动方程.通常将摄动力Fε分解成径向S、横向T（与径向垂直）和轨道面法向W三个分量，或分解成切向U（航天器飞行方向）、轨道面内主法向N（与切向垂直）和轨道面法向W（亦称次法向）三个分量，航天器的运动在轨道平面内分径向分量与横向分量，但由于摄动力的影响，Ω、i并非常值，轨道平面也在变化.

若选择以S、T、W表示轨道摄动加速度分量，则相应的高斯型摄动运动方程如下：

3.2 适用于任意偏心率（0≤e＜1）的摄动运动方程

由式（18）可见，e＝0是摄动运动方程的奇点，当e＝0时，ω不确定，M不确定，为此对于近圆轨道可定义下述变量来描述轨道基本参数：

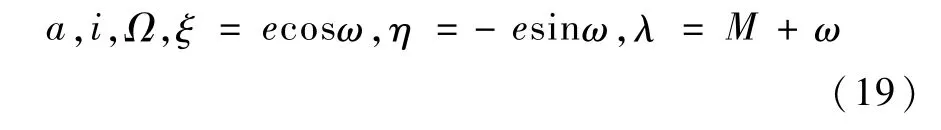
由式（19）可导出以S、T、W表示摄动加速度分量的摄动运动方程为：

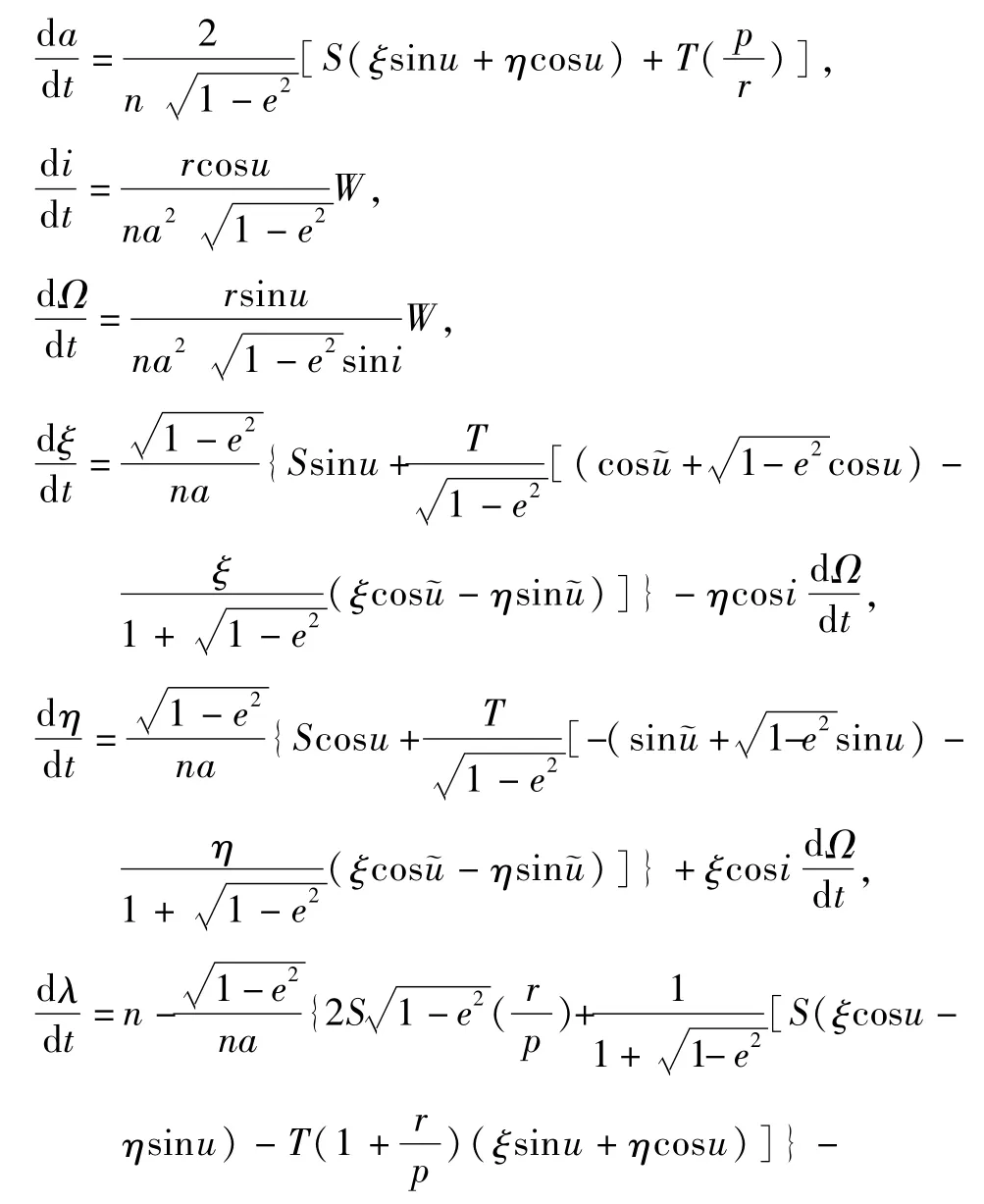
4 精确定轨［1，2，5，8］

古在由秀（Kozai）根据非线性力学中平均法的思想，针对地球引力场位函数主要带谐项（J2、J3、J4项）摄动，提出了平均根数法，它与经典摄动法联系紧密，又可直接采用几何意义明确的椭圆轨道根数作为基本变量.平均根数法将摄动项中的永年项、长周期项和短周期项区分开，将参考解取为只包含永久变化项的平均根数.为避免小偏心率问题，采用第一类无奇点根数σ＝（a i Ω ξ η λ）T，平均根数定义为：

式中：σ0为t0时刻的瞬时根数；σ1、σ2分别为一、二阶永年摄动项系数为一阶长周期摄动分别为t0时刻与t时刻的一、二阶短周期摄动；¯σ为t时刻的平均根数，σ为t时刻的瞬时根数.

除了地球形状摄动、大气阻力摄动、太阳光压摄动、日月引力摄动、小推力摄动外还有由于岁差章动和地极移动引起的坐标系摄动等，因此难以用精确的摄动计算公式去求解轨道根数，为此轨道确定采取如下方案：

1）当GPS接收机天线能够接收四颗以上导航星信息时，利用GPS接收机导航结果迭代求出摄动分量；

2）当GPS接收机不能同时接收四颗以上导航星信息，短时间不能正常导航时，利用已经导出的航天器平均根数和摄动分量，外推出此时的航天器位置矢量与速度矢量.

基于上述GPS接收机轨道确定基本思想，选择适合于任意偏心率中低轨道航天器的包含未知因子的轨道摄动计算公式如下：

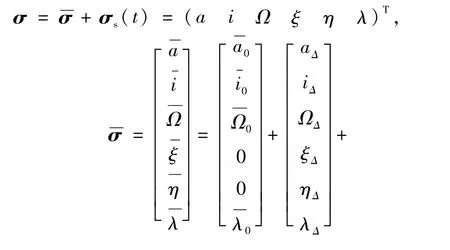
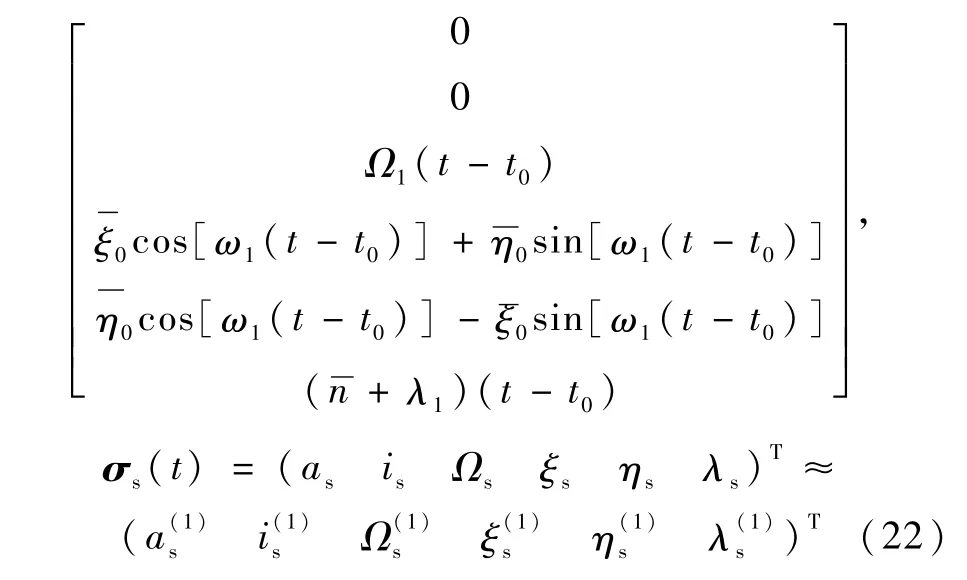
对多次求得的二阶永年项系数可采取平滑滤波方法加以改进.

若GPS接收机天线被航天器的帆板、定向通信天线等遮挡，短时期内不能正常接收到四颗GPS导航星导航信息时，则可利用式（22）外推出下一时刻的瞬时轨道根数，进而求得航天器的精确的位置矢量和速度矢量，以保证航天器导航、相对差分定位、在轨标定正常进行.

5 结论

本文给出了利用GPS接收机的导航信息精确确定接收机载体航天器的轨道根数的方法，并提出了采用接收机的导航信息与摄动运动方程式外推的组合导航方法，保证定轨精度达10m量级.

致谢

本文是根据有关项目的研究报告摘要形成的，研究报告的形成得到了王旭东、陈祖贵、高益军等专家和同事们的支持和帮助，在此特表示衷心的感谢！

［1］夏南银.航天测控系统［M］.北京：国防工业出版社，2002

［2］刘林.航天器轨道理论［M］.北京：国防工业出版社，2000

［3］中国科学院紫金山天文台.2003年中国天文年历［M］.北京：科学出版社，2002

［4］陈芳允.卫星测控手册［M］.北京：科学出版社，1993

［5］杨嘉墀.航天器轨道动力学与控制［M］.北京：宇航出版社，1995

［6］张守信.GPS卫星测量定位理论与应用［M］.长沙：国防科技大学出版社，1996

［7］ Elliott D K.GPS原理与应用［M］.邱致和，王万义译，电子工业出版社，2002

［8］汤锡生，陈贻迎，朱民才.载人飞船轨道确定和返回控制［M］.北京：国防工业出版社，2002

An Accurate Orbit Determination Technique Using GPS Receiver

SUN Baoxiang1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

This paper proposes an accurate orbit determination technique to accurately determine orbit elements of a spacecraft equipped with a GPS receiver according to navigation messages from the receiver.Accurate coordinate system and time system transformations necessary to guarantee the orbit determination accuracy of the order of 10m are presented.A combined navigation method using navigation messages from receiver and the recursive formula of the perturbation motion equation is adopted，and the navigation can still operate normally even if antennas of the receiver is obscured in a short duration.

orbit determination；orbit elements；navigation message