激发思维灵感提高解题能力

黄育粤

思维灵感往往能产生巧妙的方法,使问题获得快捷的解决,这种瞬息间萌发的灵感,使学生学习充满乐趣,学习信心倍增。

一、创设“趣境”,激发思维灵感

兴趣是推动学生学习的内部驱动力,是学生学习积极性中最现实、最活跃的心理成分。学生一旦对学习产生了兴趣,就会在大脑中形成优势兴奋中心,促使各种感官处于活跃状态,引起对学习的高度注意,为激发思维灵感提供最佳的心理准备。因此,创设“趣境”是激发学生思维灵感的首选方法。

例如,在教学“三角形的内角和”时,教师在黑板上画一个任意三角形,并告知其中二个内角的度数,让学生说出第三个内角的度数。学生面面相觑,无人应答。教师趁热激趣:“不为难大家了,请各人在纸上画一个三角形,只要说出两个内角的度数,老师就能马上帮你说出第三个内角的度数。”学生个个兴趣盎然,都想难倒老师,但一次次都被老师准确无误地答对了。学生还以为是老师“猜”出来的,也想尝试一下,却以失败而告终。最后老师讲解了“三角形的内角和是180°”的道理,学生豁然开朗。紧接着在小组内相互画三角形,进行猜角度数的活动。正当学生感到大功告成时,老师又不失时机地提出:“谁能想方设法做一些实验论证‘三角形的内角和是108°呢?”学生在知识内在魅力的激发下,又主动投入到知识的产生、发展及形成过程的探索中。

生1:老师,我是用量角器分别测量出三角形三个内角的度数,然后相加,得出三角形内角和是180°。

生2:我是用“撕”的办法,我小心“撕”下三角形纸片上的三个角,拼在一起,发现撕下的三个角能拼成一个180°的平角(见图1)

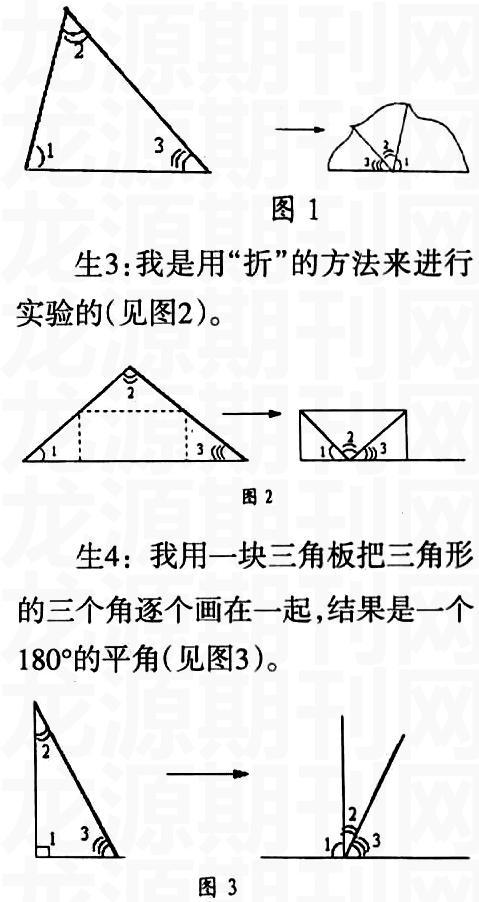
探究后,让学生说出结论:任意三角形的内角和是180°。

该“趣境”的创设十分贴切,直观地诠释了三角形内角之和。学生在浓厚的兴趣中学习数学,思维灵感得到了激发与保持,通过探索、发现、思考、验证、归纳等教学活动,最后获得数学结论,学生在自主学习中真正成为了学习的主人。

二、预设“疑境”,激发思维灵感

学生在解题时常因缺乏缜密思考,思维无序或推理无据,顾此失彼而步入理解的误区。面对这种情况,教师应适当给学生预设“疑境”,有意让学生落入“陷阱”,然后引导学生独立思考,适时组织交流,使之相互启迪,激发思维灵感,做到集思广益,探究错因,产生正确思路,探索出新的解题方法,培养学生思维的创造性。例如:“在一只底面半径是30厘米的圆柱形水桶里,有一段半径10厘米的圆柱形钢材浸没在水中,把钢材从桶中取出后,桶里的水位下降5厘米,求这段钢材长多少厘米?”解答这道题

(厘米)就不会计算错了。这样的改错激发了学生的思维灵感,学生借助钢材体积与取出钢材前后水的体积差相等的关系,找到问题的本质并获得新的解法。因为体积相等,就是底面积与高的乘积相等,所以底面积与高成反比例的量。又因钢材底面积与水桶底面积的比是1∶9,所以钢材的长度与水位下降高度的比是9∶1,因此钢材的长度是5×9=45(厘米)。

通过预设“疑境”,点燃了学生思维的火花,促进了学生思维的升华和正确思路的萌生,有效地提高了学生独立分析问题、解决问题的能力。

三、设置“困境”,激发思维灵感

在数学的发展和数学家们探究数学的过程中,充满了“困境”和战胜“困境”的方法,但数学教材不能把这些曲折的探索、猜想、发现过程一一编写进去。在教学中如果教师只教正确的方法,一算就准,一解就对,一用就灵,忽视对“困境”的剖析,学生学到的是现成的知识,一旦遇到困境,就会束手无策。因此,在数学教学中,教师应有意识地设置困境,暴露挫折与失败的过程,让学生参与到反思错因的过程中,能有效激发思维灵感,获得走出困境的方法,提高免疫能力,防止重蹈覆辙。

例如:“暑假里,小明计划用5天时间做完一本描红簿,由于每天多描红36个字,结果提前了2天做完。小明原计划平均每天描红几个字?”解答时,学生大都按习惯了的解题思路:要求“原计划平均每天描红几个字”,必须先要已知“原计划做完一本描红的字数”和“原计划做完的天数”两个条件。其“原计划5天做完”已经直接告诉,但是“原计划做完一本描红簿的字数”从题目条件中无法预先求出,因此,这条解答思路碰了壁。必须引导学生回过头来重新分析题目中条件与条件、条件与问题之间的数量关系,学生发现做完同一本描红簿,原计划5天做完,而实际只用了(5-2)天做完,提前了2天,什么原因呢?让学生讨论。由于问在点子上,启发在关键处,学生恍然大悟,有了思维灵感,“由于每天多描红36个字”,结果在实际描红的3天里,比原计划的3天里多描红(36×3)个字,所以提前了2天。这就是说,原计划2天的描红量是108个字,问题得以解决,这种思维灵感源于对困境的剖析。可见遇到挫折,挖掘错因,经过反思,调整思维方向,就能获得成功。

四、营造“挑战”情境,激发思维灵感

由于小学生的好胜心、好奇心和表现欲都很强,只要联系学生的生活经验和认知水平选择学生感兴趣的数学素材,就可营造具有现实性、挑战性的问题情境,使学生处于心欲求而不得,口欲言而不能的“愤悱”状态,激活他们强烈的挑战心理,进而引导他们在探究新知的过程中不断产生灵感,做到随机应变,运用自如。

例如,在学生掌握了“圆柱体体积的计算”后,教师先让学生完成如下基础练习:已知圆柱体的底面积(或半径、直径、周长)和高,求体积。正当学生利用求积公式顺利解答,沾沾自喜时,教师拿出一个大苹果,问:“这个苹果的体积有多大?”学生充满了困惑。这时教师用富有挑战性的口吻问:“谁能算出它的体积?这个苹果就奖给他!”教师有效激发了学生的思维灵感,同学们提出了很多解答思路,如:把苹果切开后转化成正(长)方体或圆柱体,求出苹果体积的近似值;把苹果浸入盛满水的杯子里,把溢出的水倒入量杯,量得溢出的水的体积,就是苹果的体积;把苹果浸入装有水的量杯中,根据水位上升的高度可以求出苹果的体积;先把苹果放入空量杯,然后倒满水,再从量杯中取出苹果,根据水位下降的刻度求出苹果的体积;先求出1立方厘米苹果的重量,再称出这个苹果的重,就可以计算出苹果的体积……就这样,学生在相互交流中受到启发,激发了思维灵感,切实提高了解决问题的技巧。

作者地址

福建省福安市实验小学

◇责任编辑:曹文◇