教学活动中突出学生的“亲历性”

张兴兰

《数学课程标准》指出:“教师应激发学生的学习积极性,向学生提供充分从事数学活动的机会,帮助他们在自主探索和合作交流过程中真正理解与掌握基本的数学知识技能、数学思想和方法,获得广泛的数学活动经验。”基于这样的理念,我认为要使学生变被动接受为主动探索,在教学活动中就要突出学生的“亲历性”,注重引导学生亲身经历发现规律、揭示问题、探究知识、归纳结论等数学活动,让学生亲身体验数学知识的产生、发展过程,使课堂真正成为“天高任鸟飞、海阔凭鱼跃”的乐学天地。

规律让学生去发现

宇宙中的一切事物变化无穷,但它们总是按照一定规律变化着,只不过这些规律有的已被人们发现,有的暂时未被发现。如果教师总是把前人总结出来的规律和盘托出,学生也许感觉不到它有什么奥秘;如果教师能引导学生在一定的情境中去发现,那滋味肯定会令学生回味无穷。著名数学教育家乔治·波利亚有句名言:“学习任何知识的最佳途径是由自己去发现。因为这种发现理解最深,也最容易掌握其中的内在规律、性质和联系。”

如学习了平面图形的面积计算后,我设计了这样一个实践活动:

师:学校食堂后面有一块空地,现准备用24米长的篱笆把它围起来,怎样才能使里面种的菜最多呢?

生1:围成的空地面积最大,种的菜就最多。

生2:围成正方形的面积最大,因为在周长相等的情况下,三角形、梯形、长方形、平行四边形的面积都没有正方形大。

师:很好!还有什么办法能使围成的地方更大?

生3:如果有一边靠墙,不用篱笆,围成的地方肯定会更大。

师:这种方法妙!那围成什么形状的面积最大呢?

生(异口同声):当然是正方形!

师:是吗?大家不妨动手设计几种方案,比较一下。

经过合作、讨论,学生们设计出如下方案:

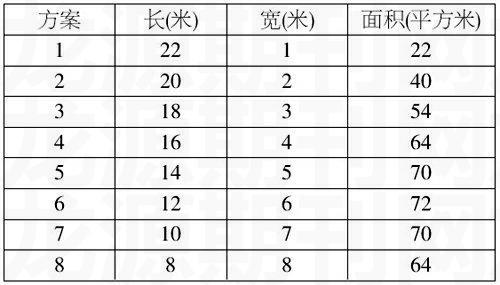
师:仔细观察这些不同方案,你们有什么新的发现?

生4:围成的正方形面积不是最大的,围成的长方形面积最大。

生5:不准确,只有当长是宽的2倍时,围成的长方形面积才是最大。

生6:还要说明周长相等,一面靠墙等情况。

……

这一教学过程,学生经历了猜想、讨论、验证等一系列学习活动,终于发现了一个教材中没有的规律,对学生而言,这种“发现”具有创造性,实在难能可贵。另外,学生在“发现”过程中的学习并不是简单的信息积累,更主要的是包含了新旧知识经验的冲突,以及由此而引起认知结构的重组。

问题让学生去揭示

在教学活动中,我们应千方百计创设一些情境,让学生带着一个个“?”走进教室,又让学生带着一个个新的“?”走出教室。如教学“圆的认识”时,一上课我就让学生玩“甩小球”的游戏,并发问:“在甩小球的过程中,你们都想到了哪些问题?”这下学生们可带劲儿了,争着说:“为什么有的同学甩的圆大,有的同学甩的圆小?”“圆的大小与什么有关系?”“为什么球在空中运动的路线不是长方形、三角形的,而是圆形的?”……新课伊始,通过活动引导学生主动地去揭示问题,这样学生就会带着一种好奇去分析问题,找到问题的答案。新课结束时,我又抓住时机设问:“刚才同学们已经知道了汽车的车轮为什么要设计成圆的,在我们日常生活中还有哪些物体的面是圆的呢?”学生很快说出:瓶盖、钟面、硬币面、十字路口的花坛……我问:“关于这些物体,你们又想到了哪些问题呢?”学生的脑海里又泛起了疑问的波澜,课后学生肯定少不了要去讨论研究、去调查了解、去查阅资料、去大胆想象。

知识让学生去探究

自主探究是学生运用已有的知识和经验解决新问题的一种学习方式。苏霍姆林斯基说过:“在人的心灵深处,总有一种根深蒂固的需要,这就是希望自己是一个发现者、研究者、探索者。”教育心理家研究表明,儿童的这种欲望尤为强烈。因此,在教学活动中,我们应放手让学生自己去探索、去观察、去讨论合作,感受知识的产生和发展过程,满足学生的成就感。要使学生学会探究,就得为学生营造一个主动探究的氛围,为学生提供充足的时间和自由的空间。如教学“小数除法”时,我先创设情境,引出34.8÷24、32.4÷48等算式,接着让学生独立尝试用竖式计算,然后引导学生分小组合作交流:“在试做过程中,你遇到了哪些问题?是怎样解决的?”最后,在集体交流评议时,各组的代表争着发言:“我们在计算34.8÷24时,发现除到被除数的末尾还有余数,我们小组的意见是在余数后面添0再除。”“我们认为先要在被除数的末尾添0,再把0落下来继续除。”“我们认为在被除数末尾添0可省去不写,因为根据小数的性质可以证明在34.8末尾添上0,34.8的大小没变。”“我在计算32.4÷48时,发现用32除以48不够除,我认为应该在被除数的个位上商0,但同组同学不同意,不知大家的意见怎样?”“我估算了一下,32.4÷48,商应该是零点几,如果商的个位不写0的话,那商不就变成675了?”……听了学生的发言,我高兴地说:“理真是越辩越明啊!”这一教学活动,学生在个人自主学习的基础上,通过小组讨论、协作、集体交流评议,进一步完善和深化了对小数除法算理的建构。

结论让学生去归纳

归纳是一种重要的数学思想。它是学生在充分感知的基础上,运用比较准确简洁的语言对某一算理、定义、法则、公式、性质定律等进行概括。这一过程是由感性认识上升到理性认识,是认识的一次飞跃。归纳的过程不仅使学生更加深刻地理解所学内容,而且也发展了学生的学习能力。

总之,在教学活动中,我们应关注学生的发展,把提问的权利交给学生,把探究的空间还给学生,把发现的机会让给学生,把归纳的时间留给学生,为每个学生搭起一个充分证明自己、展示自己的舞台。