围长为2的本原无限布尔方阵类的本原指数集

张德全,李修清

(桂林航天工业高等专科学校计算机系,广西桂林 541004)

围长为2的本原无限布尔方阵类的本原指数集

张德全,李修清

(桂林航天工业高等专科学校计算机系,广西桂林 541004)

研究了围长为2的无限布尔方阵的本原性,通过无限有向图D(A)的直径给出了这类矩阵的本原指数的上确界,最后证明了直径小于等于d且围长为2的本原无限布尔方阵所构成的矩阵类的本原指数集为={2,3,…,3d}.

无限布尔方阵;本原指数;有向图;直径

1 引言

设β={0,1}是由两个元素所组成的布尔代数,具有布尔加法:a+b=max{a,b}和布尔乘法:a·b=min{a,b},这里β={0,1}中约定0＜1.定义在β={0,1}上的具有无限行和无限列的矩阵称为无限布尔方阵.按通常矩阵的加法、数量乘法和矩阵乘法,我们给出无限布尔方阵的加法,数量乘法和乘法的定义.

定义1设A=(aij),B=(bij)都是无限布尔方阵,λ∈β,

由无限布尔方阵的乘法定义,无限布尔方阵的幂运算是有意义的,设A是一个无限布尔方阵,若存在有限的正整数k,使Ak＞0(即Ak中的每个元素均为1),则称A是本原无限布尔方阵(简称本原的),使Ak＞0成立的最小正整数k称为A的本原指数,记作γ(A)=k.设A=(aij)是一个无限布尔方阵,则A可自然地对应一个无限阶有向图D(A)=(V,E),其中V={v1,…,vn,…}是顶点集,E是弧集,aij=1当且仅当有弧(vi,vj)∈E(i,j=1,2,… ),称为A的伴随有向图,显然有向图D(A)=(V,E)中可以有自环,但没有重复弧.

无限布尔方阵的本原性可以自然地用图的语言表述,设D是一个无限阶有向图(图中允许有自环,但不允许有重复弧),若存在有限的正整数k,使得任取图中两点i,j,对于任意一个≥k的正整数m,都有点i到点j长为m的途径,且图D中存在两点u,v,使得点u到点v没有长为k−1的途径,则称D是本原有向图,且称k为D的本原指数,记作γ(D)=k.显然,A是本原无限布尔方阵的充分必要条件是A的伴随有向图D(A)为本原有向图,且γ(A)=γ(D(A))；因此研究无限布尔方阵的本原性及其本原指数集就完全等同于研究相应的伴随有向图的本原性及其指数集.

若A=(aij)是一个无限布尔方阵,且主对角线上的元素均为零且至少有一对非零对称元,则A对应的伴随有向图D(A)=(V,E)是一个没有自环且最小圈长为2的无限阶有向图,我们将一个图的最小圈长称为这个图的围长,这样主对角线上的元素均为零且至少有一对非零对称元的无限布尔方阵的伴随有向图是一个围长为2的无限阶有向图,反之一个围长为2的无限阶有向图的邻接矩阵也是一个主对角线上的元素均为零且至少有一对非零对称元的无限布尔方阵.

通过D(A)的直径估计本原矩阵A的本原指数是一个十分有意义的课题,关于n阶本原矩阵的本原指数,文[2]给出了n阶对称本原矩阵本原指数的上界估计:γ(D)≤2d,文[3]给出了一般的n阶本原矩阵的本原指数上界估计:γ(A)≤d2+1,其中d为D(A)的直径.但对于无限布尔方阵A通过D(A)的直径来估计A的本原指数及本原指数集等问题的研究还很不深入,文[1]中研究了含有非零对角元的无限布尔方阵,通过D(A)的直径给出了其本原指数的上界估计,并给出了这类矩阵的本原指数集的刻划,文[4]中研究了对称无限布尔方阵,并通过D(A)的直径给出了对称本原无限布尔方阵的本原指数集的刻划.本原指数研究的另一个方面是对各种特殊的本原矩阵类的本原指数以及本原指数集的研究.本文研究主对角线上的元素均为零且至少有一对非零对称元的一类无限布尔方阵,即伴随有向图D(A)的围长为2的一类无限布尔方阵,记这类方阵的集合为B0,即B0={A|A是无限布尔方阵,且伴随有向图D(A)的围长为2};本文研究这类无限阶布尔方阵的本原性,通过伴随有向图D(A)的直径给出本原指数的上确界,最后给出直径小于等于d的围长为2的本原无限布尔方阵所构成的矩阵类的本原指数集的刻划.

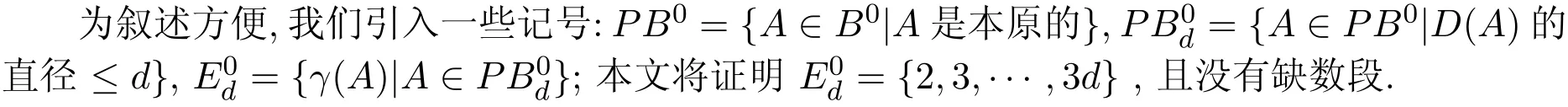
2 B0中无限布尔方阵为本原阵的一个充分必要条件

设D是一个无限阶有向图,i,j是图中的两个顶点,k是一个正整数,若从顶点i到顶点j有长为m≥k(其中m是大于或等于k的任意一个正整数)的途径,但从顶点i到顶点j没有长为k−1的途径,则称k为顶点i到顶点j的局部本原指数,记作γ(i,j)=k;由以上对无限阶有向图D的本原性以及图D的本原指数的定义,显然可得:

命题2设D是一个无限阶有向图,则D是本原的当且仅当集合{γ(i,j)|i,j∈V(D)}是有限集,且当D是本原图时有γ(D)=max{γ(i,j)|i,j∈V(D)}.

设D(A)=(V,E)是无限布尔方阵A的伴随有向图,i,j是图中的任意两个顶点(这两点可以相同也可以不同),若既有从顶点i到顶点j的长度有限的途径,也有从顶点j到顶点i的长度有限的途径,则称图D(A)是强连通图,称A为不可约无限布尔方阵(简称不可约的);本文用d(i,j)表示顶点i到顶点j的距离,若集合{d(i,j)|i,j∈V(D)}是有界集,则称D(A)具有有限的直径,并称max{d(i,j)|i,j∈V(D)}为D(A)的直径,记作d(D(A));为了方便我们将有向图D(A)具有有限直径也称为A具有有限的直径,将D(A)的直径也称为A的直径;用RD(A)表示D(A)的所有有限圈(有限圈:即长度有限的圈)的长度的集合,即RD(A)={r|r为D(A)中有限圈的长度}.

下面给出B0中无限布尔方阵为本原阵的一个等价刻划.首先给出Schur的一个引理.

引理1[5](Schur)设k≥2,ri(i=1,2,…,k)是正整数,且gcd(r1,r2,…,rk)=1,则存在仅与r1,r2,…,rk有关的非负整数N(r1,r2,…,rk),当n≥N(r1,r2,…,rk)时,方程r1x1+…+rkxk=n有非负整数解.

我们把使引理1成立的最小的非负整数N(r1,r2,…,rk)记作φ(r1,r2,…,rk),称为r1,r2,…,rk的Frobenius数,特别当k=2时有:φ(r1,r2)=(r1−1)(r2−1).

设R={r1,r2,…,rk}⊆RD是无限阶有向图D中k个不同的圈长,且gcd(r1,r,…,rk)= 1,D中从顶点i到顶点j且和长度分别为r1,r2,…,rk的圈都接触(只要和一个长为r的圈有公共点就称为接触了长为r的圈)的最短途径长记为dR(i,j),称为从顶点i到顶点j的相应于R的广义相对距离,记φR为r1,r2,…,rk的Frobenius数,即φR=φ(r1,r2,…,rk),则显然顶点i到顶点j有长为m的途径,其中m大于等于dR(i,j)+φR的任意一个正整数,从而由局部本原指数的定义有:γ(i,j)≤dR(i,j)+φR.即

引理2设R={r1,r2,…,rk}⊆RD是无限阶有向图D中k个不同的圈长,且gcd(r1,r2, …,rk)=1,任取D中i,j两点,则顶点i到顶点j有长为m≥dR(i,j)+φR的途径,从而有γ(i,j)≤dR(i,j)+φR.

文[1]中给出了无限布尔方阵为本原阵的一个等价刻划.

定理1[1]设A是一个无限布尔方阵,D(A)是A的伴随有向图,RD={D(A)中所有有限圈的长度},则A是本原阵的充分必要条件为:

(i)D(A)是强连通有向图;

(ii)D(A)有有限直径,存在RD中的有限元素r1,r2,…,rk且满足gcd(r1,r2,…,rk)=1.

由定理1,我们易给出B0中的无限布尔方阵为本原阵的一个充分必要条件.

定理2设A∈B0,D(A)是A的伴随有向图,则A是本原阵的一个充分必要条件为:

(i)D(A)是强连通有向图;

(ii)D(A)具有有限的直径,且D(A)含有奇圈.

3 PB0中直径为d的无限布尔方阵的本原指数的上确界

情形1若y1和y2中至少有一个为0,不妨设y1=0,则有x1+k0≡2k0−y1≡0(mod 2),即x1+k0＜2k0且为偶数,由上述讨论知在图D(A)中存在一条u0点到u2点的长度为x1+k0的偶途径,矛盾.

情形2若y1和y2均为1,则x1+x2≡2k0−(y1+y2)≡0(mod 2),即x1+x2是一个小于2k0的偶数,则同样u0点到u2点存在一条长度为x1+x2的偶途径,矛盾.

于是我们就证明了假设是错误的,故定理结论成立.

定理3设A∈PB0,且D(A)的直径为d,则γ(A)≤3d,并且上界是可以达到的.

证明因为A∈PB0,由定理2知D(A)具有有限的直径,设D(A)的直径为d,由A∈PB0知,D(A)是一个没有自环且至少含有一个2圈的本原图,设D(A)的一个2圈为Γ2,且设Γ2上的两个点为i,j,则i,j点在图D(A2)中均有自环,由引理3知D(A2)的直径≤d,于是图D(A2)中i点或j点到图D(A2)中的任何一点都有长度恰为d的途径,从而在图D(A)中i点和j点到图D(A)中的任何一点都分别有长度恰为2d的途径;在图D(A)中任取两点u,v,由于D(A)的直径为d,易知从u点用长度恰为m≥d(m是不小于d的任意一个正整数)的途径可以到达图D(A)中的i点或j点,而i点或j点又可用长度恰为2d的途径到达图D(A)中的v点,于是对于图D(A)的任意两点u,v,u点到v点都存在长度恰为m+2d(m≥d是任意一个正整数)的途径,于是由局部本原指数的定义得:γ(u,v)≤3d,注意到u,v两点的任意性得γ(A)≤3d;上界的可达性证明由下一节给出.

4 无限布尔方阵类PB0的本原指数集的刻划

定理4={2,3,…,3d}(d≥3).

本文我们使用下列记号:设D是一个无限阶有向图,用(i,j)表示顶点i到顶点j的一条弧,[i,j]表示顶点i到顶点j之间的双向连通边,即一个2圈.

定理5{2,3,…,d+1,d+2}⊆(d≥3).

证明(1)设3≤k≤d(d≥3),考虑下列无限阶有向图D=D(V,E),其中V= {1,2,…,d,…},E={(1,2),(2,3),…,(k−2,k−1),[k−1,k];(k,1),(k,2),…,(k,k−2); [k,k+1],[k,k+2],[k,k+3],…}.易知,图D=D(V,E)强连通,没有自环,有2圈和3圈,且直径≤d,即D=D(V,E)的邻接无限布尔方阵A∈P;取图D=D(V,E)中圈长为2和3的集合R={2,3},则由引理1知,Frobenius数φR=2,考虑图中1点和k+1点,显然dR(1,k+1)=k,于是由引理2知γ(1,k+1)≤k+2,但1点到k+1点显然没有长为k+1的途径,故有γ(1,k+1)=k+2,另一方面易知dR(i,j)≤k(i,j=1,2,3,…),于是有γ(i,j)≤k+2(i,j=1,2,3,…),故有γ(D)=k+2(3≤k≤d),即{5,6,…,d+1,d+2}⊆;

(2)考虑主对角线上的元素均为零,其余元素均为1的无限布尔方阵A,易知γ(A)= 2即2∈;

(3)考虑下列无限有向图D=D(V,E),其中E={[1,2],(3,1);[i,j](i/=j且i,j= 2,3,…)},V={1,2,…,d,…}.显然D=D(V,E)强连通,没有自环,有2圈和3圈,且直径为2,则D所对应的邻接无限布尔方阵A∈P;易验证A和A2都不是全1矩阵,而A3是全1矩阵,于是γ(A)=3即γ(D)=3,所以3∈

(4)考虑下列无限有向图D=D(V,E),其中V={1,2,…,d,…},E={[1,2];[2,3],[2,4],[2,5],…;[3,4]}.显然图D=D(V,E)强连通,没有自环,有2圈和3圈,且直径为2,即所对应的无限布尔方阵A∈P;取图D=D(V,E)中圈长的集合R={2,3},考虑图中1点和5点,显然dR(1,5)=2,Frobenius数φR(2,3)=2,于是γ(1,5)≤4,但显然1点到5点没有长为3的途径,故有γ(1,5)=4,另一方面显然dR(i,j)≤2(i,j=1,2,3,…),于是有γ(i,j)≤4(i,j=1,2,3,…),故γ(D)=4,即4∈.

定理6{d+3,d+4,…,2d}⊆(d≥3).

证明设3≤k≤d(d≥3),考虑下列无限阶有向图D=D(V,E),其中V= {1,2,…,d,…},E={[1,2],[2,3],[3,4],…;[k−2,k−1],[k−1,k];(k,k+1),(k+1,k+2),…,(d−1,d),(d,d+1);(d+1,1);(3,1),(4,2),…,(k,k−2);[2,d+2],[2,d+3],[2,d+4],…}.易知,图D= D(V,E)强连通,没有自环,有2圈和3圈,且直径=d,即D=D(V,E)的邻接无限布尔方阵A∈P;取图D=D(V,E)中圈长为2和3的集合R={2,3},则Frobenius数φR=2,考虑图中k+1点和d+1点,显然dR(k+1,d+1)=(d−k)+(d+1),由引理2知,γ(k+1,d+1)≤2d−k+3,显然k+1点到d+1点没有长为2d−k+2的途径,故有γ(k+1,d+1)=2d−k+3;另一方面显然dR(i,j)≤2d−k+1(i,j=1,2,3,…),于是有γ(i,j)≤2d−k+3(i,j=1,2,3,…),故有γ(D)=2d−k+3(3≤k≤d),即{d+3,d+4,…,2d}⊆,(d≥3).

定理7当d为奇数时,{2d+1,2d+2,…,3d}⊆,(d≥3).

证明(1)设4≤k≤d+2(d≥3),考虑下列无限阶有向图D=D(V,E),其中V= {1,2,…,d,…},E={(1,2),[2,3],(3,4);[4,5],[5,6],…,[k−2,k−1];(k−1,k),(k,k+1), (k+1,k+2),…,(d,d+1),(d+1,d+2);(1,3),(2,4);(d+2,1);[3,3+d],[3,d+4],[3,d+ 5],…;(d+3,1),(d+4,1),(d+5,1),…}.易知,图D=D(V,E)强连通,没有自环,有2圈和只有长为d+2的奇圈,且直径=d,即D=D(V,E)的邻接方阵A∈P;取图D=D(V,E)中圈长为2和d+2的集合R={2,d+2},则由引理2知,Frobenius数φR=d+1,考虑图中k点和d+2点,显然dR(k,d+2)=(d+2−k)+(d+1),于是由引理2知γ(k,d+2)≤3d−k+4,易知k点到d+2点没有长为3d−k+3的途径,故有γ(k,d+2)=3d−k+4,另一方面易证dR(i,j)≤2d−k+3(i,j=1,2,3,…),于是有γ(i,j)≤3d−k+4(i,j=1,2,3,…),故有γ(D)=3d−k+4(4≤k≤d+2),即{2d+2,2d+3,…,3d}⊆,(d≥3);

(2)考虑下列无限阶有向图D=D(V,E),其中V={1,2,…,d,…},E={[1,2];(2,3), (3,4),…,(d−1,d),(d,d+1);(d+1,1);[2,d+2],[2,d+3],[2,d+4],…;[1,d+2],[1,d+3],[1,d+ 4],…}.易知,图D=D(V,E)强连通,没有自环,有2圈和3圈,且直径=d,即D=D(V,E)的邻接无限布尔方阵A∈P;取图D=D(V,E)中圈长的集合R={2,3},则Frobenius数φR= 2,考虑图中3点和d+1点,显然dR(3,d+1)=(d−2)+(d+1),于是γ(3,d+1)≤2d+1,且易知3点到d+1点没有长为2d的途径,故有γ(3,d+1)=2d+1,另一方面易证dR(i,j)≤2d−1(i,j=1,2,3,…),于是有γ(i,j)≤2d+1(i,j=1,2,3,…),故有γ(D)=2d+1,即2d+1∈(d≥3);综合(1),(2)就证明了,当d为奇数时{2d+1,2d+2,…,3d}⊆,(d≥3且为奇数).

定理8当d为偶数时,{2d+1,2d+2,…,3d}⊆,(d≥3).

证明(1)4≤k≤d+2(d≥3),考虑下列无限阶有向图D=D(V,E),其中V= {1,2,…,d,…},E={(1,2),[2,3],(3,4);[4,5],[5,6],…,[k−2,k−1];(k−1,k),(k,k+1),…,(d, d+1),(d+1,d+2);(1,3),(2,4);(d+2,1);[3,d+3],[3,d+4],[3,d+5],…;(d+3,1),(d+ 4,1),(d+5,1),…}.易知,图D=D(V,E)强连通,没有自环,有2圈,且只有长为d+1的奇圈且直径=d,即D=D(V,E)的邻接方阵A∈P;取图D=D(V,E)中圈长为2和d+1的集合R={2,d+1},则Frobenius数φR=d,考虑图中k点和d+2点,显然dR(k,d+2)=(d+2−k)+(d+1),于是γ(k,d+2)≤3d−k+3,且易知k点到d+2点没有长为3d−k+2的途径,故有γ(k,d+2)=3d−k+3,另一方面易证dR(i,j)≤3d−k+3(i,j= 1,2,3,…),于是有γ(i,j)≤3d−k+3(i,j=1,2,3,…),故有γ(D)=3d−k+3(4≤k≤d+2),即{2d+1,2d+2,…,3d−1}⊆,(d≥3).

(2)考虑下列无限阶有向图D=D(V,E),其中V={1,2,…,d,…},E={[1,2];(2,3), (3,4),…,(d−1,d),(d,d+1),(d+1,d+2);(1,3);(d+2,1),(d+2,2);[2,d+3],[2,d+4],[2,d+ 5],…;(d+3,3),(d+4,3),…;(d+2,d+3),(d+2,d+4),(d+2,d+5),…}.易知,图D= D(V,E)强连通,没有自环,有2圈,且只有长为d+1的奇圈,且直径=d,即D=D(V,E)的邻接方阵A∈P;取图D=D(V,E)中圈长的集合R={2,d+1},则Frobenius数φR=d,考虑图D=D(V,E)中3点和d+2点,显然dR(3,d+2)=(d−1)+(d+1),于是γ(3,d+2)≤3d,且易知3点到d+2点没有长为3d−1的途径,故有γ(3,d+2)=3d,另一方面易证dR(i,j)≤2d(i,j=1,2,3,…),于是有γ(i,j)≤3d(i,j=1,2,3,…),故有γ(D)=3d,即3d⊆,(d≥3).(且d为偶数);

综合(1)、(2)就证明了,当d为偶数时,{2d+1,2d+2,…,3d}⊆(d≥3且d为偶数).综合定理5到定理8我们就证明了定理4的结论成立.

[1]李修清,王敏.一类本原无限布尔方阵的本原指数集的刻划[J].数学的实践与认识,2007,37(1):100-103.

[2]Delorme C,Sole P.Diameter,covering index,covering radius and eigenvalues[J].Europ.J.Combinatorics, 1991,12:93-108.

[3]Jian Shen.Proof of a conjecture about the exponent of primitive matrices[J].Linear Algebra Appl.,1995, 216:185-203.

[4]李修清,王敏.对称无限布尔方阵的本原指数集的刻划[J].系统科学与数学,2008,28(12):1478-1485

[5]柳柏濂.组合矩阵论[M].北京:科学出版社,1996.

On primitive exponent set for the class of primitive infinite Boolean matrices with girth 2

ZHANG De-quan,LI Xiu-qing
(Department of Computer Science,Guilin College of Aerospace Technology,Guilin541004,China)

This paper studies the primitiveness of infinite Boolean matrices with girth 2.And it offers the least upper bound of the primitive exponent through the diameter of the infinite digraph D(A).In the end we completely determine the primitive exponent set of the matrices which are class of primitive infinite Boolean matrices with girth 2 and whose diameters are not more than d is={2,3,…,3d}.

infinite Boolean matrices,primitive exponent,digraph,diameter

O157.5

A

1008-5513(2009)03-0464-06

2008-12-30.

广西区教育厅科研项目(桂教科研[2006]26号).

张德全(1959-),副教授,研究方向：组合数学.

2000MSC:05C50