三角代数上的广义Jordan导子

马飞,朱小龙,赵建堂

(1.咸阳师范学院数学与信息科学学院,陕西咸阳 712000; 2.宁夏师范学院数学与计算机科学学院,宁夏固原 756000)

三角代数上的广义Jordan导子

马飞1,朱小龙2,赵建堂1

(1.咸阳师范学院数学与信息科学学院,陕西咸阳 712000; 2.宁夏师范学院数学与计算机科学学院,宁夏固原 756000)

主要研究了三角代数上的广义Jordan导子.利用三角代数上广义Jordan导子和广义内导子的联系,证明了作用在一个含单位元的可交换环上的三角代数到其自身上的环线性广义Jordan导子是一个广义导子.

广义Jordan导子;广义内导子;广义导子;三角代数

1 引言

在本文中,我们用R表示含单位元I的可交换环,A是作用在环R上的代数,M是A-双模.如果R是一个含单位元的可交换环,A是作用在R上的一个代数,我们称一个映射∆从代数A到其双模M是环线性的(R-线性),如果对于任意的a,b∈A和任意的r∈R,都有∆(a+b)= ∆(a)+∆(b)和∆(ra)=r∆(a)(见文[1]).若对于任意的a∈A,当2a=0时有a=0,则称A是2-非挠的.在本文中假设R,A,M都是2-非挠的.设∆是一个从A到其双模M的R-线性映射.如果对于任意的a,b∈A,都有

则称∆是一个广义Jordan导子;特别地,如果∆(I)=0,则称∆是一个Jordan导子.若对任意的a,b∈A,都有

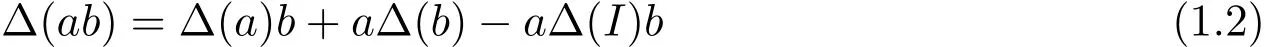
则称∆为广义导子;特别地,若∆(I)=0,则称∆为导子.若对于任意的a∈A,存在s,t∈M使得∆(a)=as+ta,则称∆是代数A到其双模M上的一个广义内导子;特别地,如果s=−t,则称∆为内导子.

由上述定义可知,(广义)内导子一定是(广义)导子,(广义)导子一定是(广义)Jordan导子,但反之一般不成立[24].那在哪些代数上成立呢?许多学者都已经研究过这个问题,比如Herstein[5]证明了每一个2-非挠的素环到其自身上的Jordan导子都是一个导子,并且在素环上不存在反导子.Breˇsar[6]证明了每个从2-非挠的半素环到其自身的Jordan导子是一个导子.张建华[7]证明了套代数上的每个Jordan导子是导子,因此是内导子.朱军[8]证明了2-非挠的半素环到其自身上的广义Jordan导子是一个广义导子.还有其他的一些类似结果在文[9-15]中也可以找到.

本文主要就是研究了含单位元的三角代数

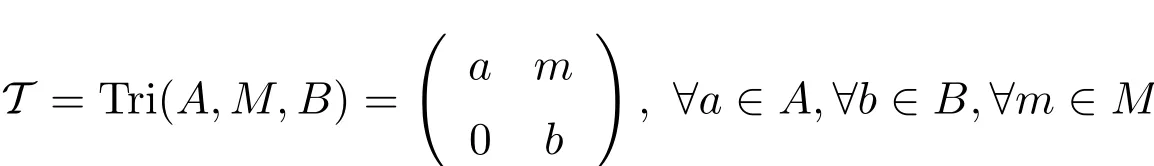
其中M是(A,B)-双模,即是A的一一左模,B的一一右模,到其自身的广义Jordan导子.文[3]证明了每个上三角矩阵到其代数双模上的广义Jordan导子是一个广义导子与反导子的和,特别是到其自身的广义反导子是平凡的,张建华等[16]证明了每个三角代数上的Jordan导子是一个导子.本文就是基于上面的研究结果,得出了一些结论.

2 三角代数上的广义Jordan导子

在下面,我们还是假设A,B是作用在含单位元的环R上的代数,M是作用在R上的,且既是A-左模又是B-右模.按照习惯,我们还是把M看作是按照rξ=ξr=(rI)ξ=ξ(rI),∀r∈R,∀ξ∈M作用在R上的双模,其中I是代数A,B的单位元.

命题1设∆是一个从A到其双模M的环线性映射,则下面各命题等价:

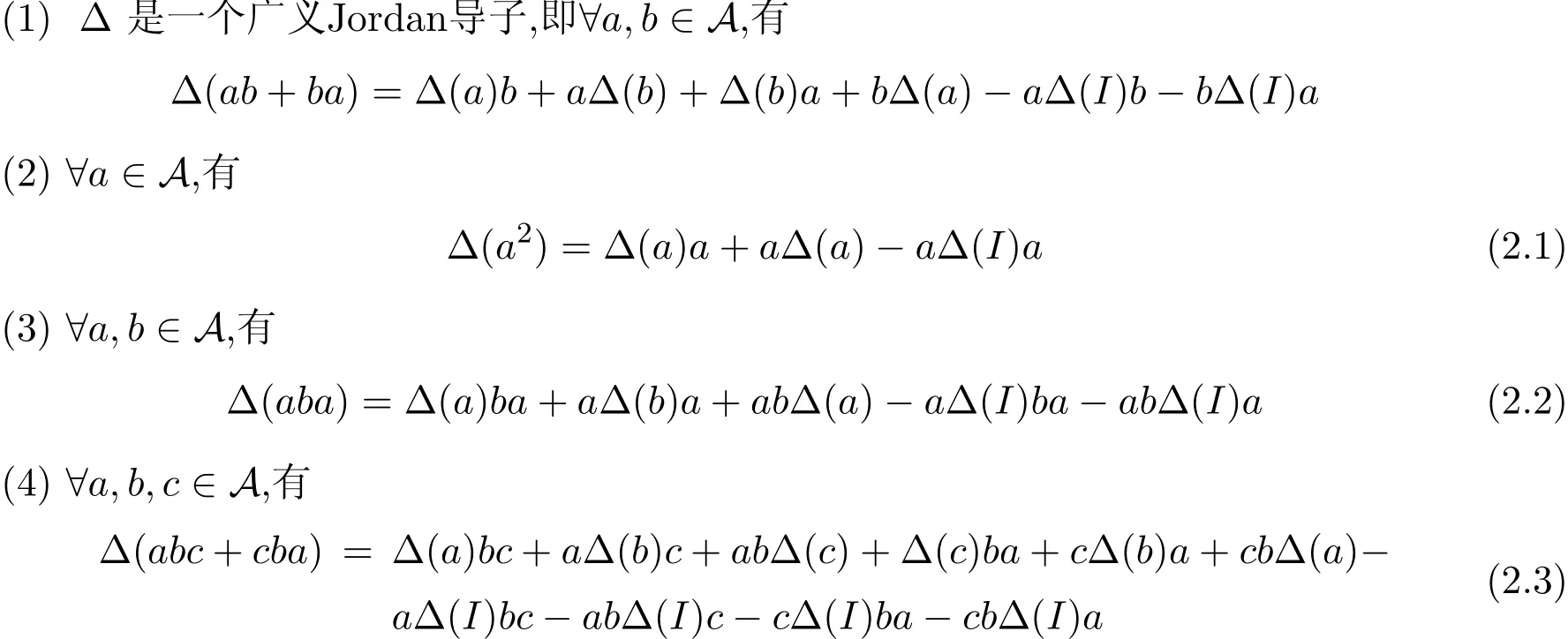
证明在文[3]中,作者已经证明了(1),(2),(3)是等价的,因此,在这里我们只需证明(1),(2),(3) 与(4)也是等价的即可.

[1]You Hong,Liu Shaowu,Zhang Guodong.Rank one preserving R-linear maps on spaces of self-adjoint operators on complex Hilbert space[J].Linear Algebra Appl.,2006,416:568-579.

[2]Benkoviˇc D.Jordan derivations and antiderivations on triangular matrices[J].Linear Algebra Appl.,2005, 397:235-244.

[3]Ma Fei,Ji Guoxing.Generalized Jordan derivation on triangular algebra[J].Linear and Multilinear Algebra, 2007,55:355-363.

[4]马飞,王红霞.广义反导子[J].纺织高校基础科学学报,2007,20:6-8.

[5]Herstein I N.Jordan derivations of prime rings[J].Proc.Amer.Math.Soc.,1957,8:1104-1110.

[6]Bresar M.Jordan derivation on semiprime rings[J].J.algebra,1989,127:218-228.

[7]张建华.套代数上的Jordan导子[J].数学学报,1998,41:205-212.

[8]Zhu Jun,Xiong Changping.Generalized derivations on rings and mappings of P-preserving kernel into range on Von neumann algebras[J].Acta math.sinica,1998,41:795-800.

[9]Cui Jianlian,Hou Jingchuan,Li Bin.Linear preservers on upper triangular operator matrix algebras[J]. Linear Algebra Appl.,2001,336:29-50.

[10]Cusack J M.Jordan derivations on rings[J].Proc.Amer.Math.soc.,1975,53:321-324.

[11]Jing Wu,Lu Shijie.Generalized Jordan derivations on prime rings and standard operator algebras[J]. Taiwanese J.Math.,2003,7(4):605-613.

[12]Johnson B E.Symmetric amenability and the nonexistence of Lie and Jordan derivation[J].Math.Proc. Cambd.Philos.Soc.,1996,120:455-473.

[13]Kadison R V.Local derivations[J].J.algebra,1990,130:494-509.

[14]Sinclair A M.Jordan homomorphisms and derivations on semisiple Banach algebras[J].Proc.Amer.Math. Soc.,1970,24:209-214.

[15]Zhu Jun.All-derivation point of operator algebras[J].Linear Algebra Appl.,2007,427:1-5.

[16]Zhang Jianhua,Yu Weiyan.Jordan derivations of triangular algebras[J].Linear Algebra Appl.,2006,419: 251-255.

Generalized Jordan derivations of triangular algebras

MA Fei1,ZHU Xiao-long2,ZHAO Jian-tang1
(1.College of Mathematics and Information Science,Xianyang Normal University,Xianyang 712000,China; 2.College of Mathematics and Computer Science,Ningxia Normal University,Guyuan 756000,China)

In this paper,generalized Jordan derivations of triangular algebra are discussed.By the relation of generalized Jordan derivation and generalized inner derivation of triangular algebra,we show that every R-linear generalized Jordan derivation of triangular algebras over a commutative ring with identity is a generalized derivation.

generalized Jordan derivation,generalized inner derivation,generalized derivation,triangular algebra

O175.26

A

1008-5513(2009)03-0595-08

2008-04-11.

咸阳师范学院科研项目(07XSYK262).

马飞(1981-),硕士,研究方向：算子代数与算子理论.

2000MSC:47L35,47B47