混合幂为2,3,a和b的丢番图不等式

李伟平,龚克

(1.河南财经学院信息学院,河南郑州 450002;2.河南大学数学与信息科学学院,河南开封 475004)

混合幂为2,3,a和b的丢番图不等式

李伟平1,龚克2

(1.河南财经学院信息学院,河南郑州 450002;2.河南大学数学与信息科学学院,河南开封 475004)

运用Davenport-Heilbronn方法证明了如果η是实数,λ1,µ1,µ2,µ3,µ4,θ1,θ2是非零实数,并且不同一符号,且至少一个λ1/µi(i=1,2,3,4)是无理数,假设(i)a=3,3≤b≤11,或者(ii)a=4,4≤b≤5,那么对某些σ=σ(a,b)＞0,混合幂为2,3,a和b的丢番图不等式有无穷多正整数解x1,…,x7.

关丢番图不等式;混合幂;Davenport-Heilbronn方法

1 引言

对于变量为正整数的混合幂丢番图不等式,文[3]证明了:令µ为实数,λ1,…,λ6为不同一符号的非零实数,且λ1/λ2是无理数.设(i)a=3,b≥3;或(ii)a=4,4≤b≤9; 或(iii)a=5,5≤b≤6,则对某些σ=σ(a,b)＞0不等式

有无穷多正整数解x1,…,x6.

文[4]证明了:设κ是实数,λ1,…,λ7为不同一符号的非零实数,且至少有一个比值是无理数.那么对0＜σ＜1/36,不等式

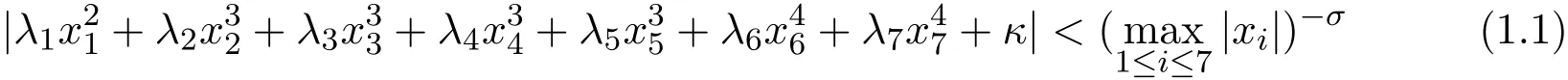
有无穷多正整数解x1,…,x7.

本文把(1.1)式中的幂数4推广为a和b.我们的结果是

定理如果η是实数,λ1,µ1,µ2,µ3,µ4,θ1,θ2是非零实数,并且不同一符号,且至少一个λ1/µi(i=1,2,3,4)是无理数,假设(i)a=3,3≤b≤11;或者(ii)a=4,4≤b≤5,那么对某些σ=σ(a,b)＞0不等式

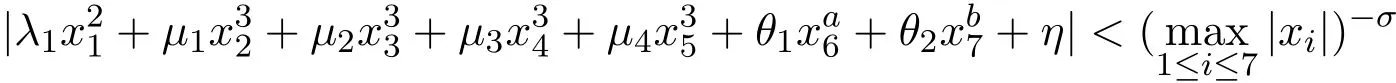
有无穷多正整数解x1,…,x7.

文[5]证明了a=b=3时的结论,当a=b=4时文[4]已证明,于是我们省去这些情形的证明.

文中我们约定σ是依赖于a和b的正数,δ是依赖于a,b和σ的充分小的正数.符号≪和≫中隐藏常数至多依赖于λ1,µ1,…,µ4,θ1,θ2,a,b和δ.记e(x)=exp(2πix).符号meas(…)表示Lebesgue测度.

2 预备引理

根据定理的要求,我们不妨假设λ1/µ1是无理数,λ1/µ1＜0.通过用2akxk代替xk(k=1,2),其中a1和a2是仅依赖于λ1,µ1,…,µ4,θ1,θ2的整数,设

3 余区间上的估计

[1]Davenport H,Helbronn H.On indefine quadratic forms in five variables[J].Journal of the London Mathematical Society,1946,21:185-193.

[2]李伟平,王天泽.一个素数,两个素数的平方以及2的若干次幂和的丢番图逼近[J].纯粹数学与应用数学, 2005,21(4):295-299.

[3]Baker R C,Harman G.Diophantine inequalities with mixed powers[J].Journal of Number Theory,1984,18:69-85.

[4]余红兵.混合幂的丢番图不等式(II)[J].数学学报,1994,37(3):324-331.

[5]Cook R J.Diophantine inequalities with mixed powers[J].Journal of Number Theory,1977,9:142-152.

[6]Danenport H.Indefine quadratic forms in many variables[J].Mathematika,1956,3:81-101.

Diophantine inequality with mixed powers 2,3,a and b

LI Wei-ping1,GONG Ke2
(1.College of Information,Henan University of Finance and Economics,Zhengzhou450002,China; 2.College of Mathematics and Information Science,Henan University,Kaifeng475004,China)

In this paper,used Davenport-Heilbronn method it is shown that:Let η be real and let λ1,µ1,µ2,µ3, µ4,θ1,θ2be nonzero real numbers,not all of the same sign,such that at least one ratio λ1/µi(i=1,2,3,4)is irrational,and suppose that either(i)a=3,3≤b≤11,or(ii)a=4,4≤b≤5,then for some σ=σ(a,b)＞0 the Diophantine inequality with mixed powers 2,3,a and b has infinitely many solutions in positive integers x1,…,x7.

Diophantine inequality,mixed powers,Davenport-Heilbronn method

O156.4

A

1008-5513(2009)03-0497-05

2008-09-28.

国家自然科学基金(10671056).

李伟平(1972-),博士,讲师,研究方向:解析数论.

2000MSC:11D75