并发Lambek演算在时态查询中的语义转换*
2009-05-08刘冬宁
刘冬宁, 汤 庸
(1.中山大学计算机科学系,广东 广州 510275; 2.中山大学数学系,广东 广州 510275)
关于时间的表达、推理与查询一直是时态数据库中最为关键的研究点。目前许多的时态查询语言已经使用于时态数据库,其理论基础也相对繁杂,但其中最为直接关联并得到广泛应用的就是基于时态逻辑的查询语言[1]。这主要是由于时态逻辑能充分体现时间的特性。然而,1994年Gabby等论证了时态逻辑是不可递归公理化的,由此它的公理化系统和证明论方法不适于时态数据库查询语言的句法分析和语义分析[2]。这使得相关形式化研究工作存在较大的遗憾,时态逻辑无法利用公理化系统的良好性质及相关证明论方法对时态数据库的推理和查询做更为严谨和细致的刻画。因此,目前用于时态数据库查询语言的时态逻辑都是非公理化的,无论其适用与否,对于计算性语言这都是一个不足。
时态逻辑之所以与时态查询密切相关,主要是因为其体现了时间的特性,在句法分析和语义分析方面都对时间的处理给予极大支持。因此,要取代时态逻辑在时态查询语言中的地位,替代者也必须能恰如其分的体现时态属性、时态关系之间的运算,并最终用于时态查询语言的句法分析和语义分析。针对此,我们曾提出:以Lambek演算[3]为核心的范畴语法系统作为句法分析工具,类型演算(λ-演算[4]作为语义分析工具,从而取代时态逻辑在时态查询中的地位。
据此,我们构建了并发的Lambek演算(LCTQ)及其范畴语法用以作时态查询的句法分析,本文将据LCTQ演算构造相应的LCTQ标号自然演绎系统,从而提供句法演算到语义计算的转换方式,为时态查询的语义分析提供相关接口。
1 LCTQ的自然演绎系统
LCTQ系统系统的类型由原子类型p1、p2…等构成,所有原子类型的集合表示为Tp。类型的有穷非空矢列集合写作Tp+。LCTQ演算的矢列形如ГA,并包含4个二元连接词·、→、←(和|。
该演算系统的自然演绎系统如下所示:
规则:


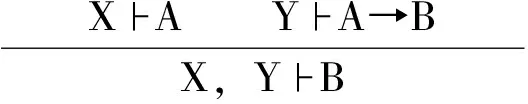

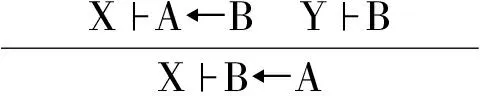
除(|El)、(|Er)、(|I)三条规则外,其余规则是经典Lambek演算L系统的全部规则,它们组成原L系统[3]。(|El)、(|Er)、(|I)三条规则是为新添加的连接符“|”加入的消去和引入规则。在消去规则中,(|El)为左消去规则,(|Er)为右消去规则。(|I)为引入规则。
定义1 如果矢列ГA在LCTQ演算中是可推导的,则写作ГLCTQ→A。
2 LCTQ的句法分析
至此,根据LCTQ,我们可以时态查询语句做相应句法分析。举例如下:

表1 人员工作履历表
我们希望查询表1中没有失业过的人员名单,该查询语句如下所示:
Select r1.Name
from works r1, works r2
where r1.Name = r2.Name
and Valid (r1) meets Valid (r2)
在这里Valid (r1)和Valid (r2)表示有效时间,这是基于ATSQL2和TempDB语法习惯的[5]。
对上例,我们可建立词汇表(LEX),如表2所示。

表2 词汇表
在这里,相关词汇类型的设置是根据范畴语法对自然语言的处理相应转换至半结构SQL语言进行处理的,我们额外添加的类型主要体现在时态类型、时态关系运算以及系统公设(即System)上。
各部分类型演算步骤分列如下:
1) “System”:系统公设,类型为n;
2) “Select r1.Name”类型演算为:((n→s)←a)·an→s;
3) “from works r1, works r2 ”类型演算为:((s→s)←f)·((f←f)·(f)·(f→(f←f))·((f←f)· f)s→s ;
4) “where r1.Name = r2.Name”类型演算为:((s→s)←s)·a·(a→(s←a))·as→s;
5) “and Valid (r1) meets Valid (r2)” 类型演算为:((s→s)←s)·(a←t)·(t|(a→(s←a))|t)·(t→a)s→s ;
6) 全句最终类型演算为:n·(n→s)·(s→s)·(s→s)·(s→s)s 。
据LCTQ演算,上述句型的类型演算最终能推出终止符类型s,使得句法分析演算停止并得到正确结果。而对于不符合句法的查询,则不能得到终止符类型s,这是由系统的可靠性和完全性保证的,限于文章篇幅,在此不做介绍。
3 LCTQ标号自然演绎系统与语义转换
Lambek演算一个最重要的优点,就是可以利用“Curry-Howard”对应理论[6-7],将处理句法分析的演算与应用于语义计算(-lambda演算对应衔接起来,其对应的公理系统为标号自然演绎系统。
根据“Curry-Howard”对应理论,我们给出LCTQ演算对应的语义演算系统的LCTQ标号自然演绎系统如下所示:
公理:
规则:


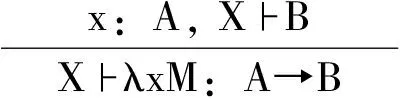
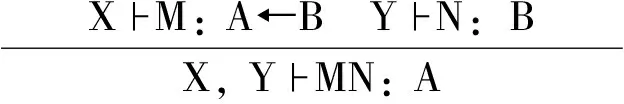
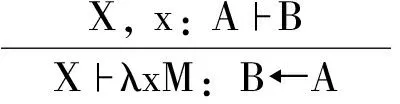
特殊地,在这里我们只对时态属性和时态关系运算做阐述和说明,其余仍和经典Lambek演算的标号系统一致[4]。
针对r1.Year和r2.Year的类型,我们可用标号系统的(←I)规则和(→I)将其λ抽象为λxM:a←t和λyN:t→a。而before的标号系统类型为P: t|(a(→s←a))t,再据(|El)和(|Er)规则,r1.Year before r2.Year的句法分析类型为:<λxM,
λ语义的抽象处理实际上是函数化和参数化的[4],其与SQL的bag语义处理方式相似程度较高,由此可以作为句法分析和语义分析的良好接口。在国际上(-演算和Lambek演算及线性逻辑的许多交叉研究成果已融入到语义网(Semantic Web)[8]、数据流程序[9](Dataflow Programming)和模糊分析信息系统[10]等人工计算语言的语义分析工作上,证明了其是有效的分析方法,值得借鉴。
4 结 语
在本文中,我们据Curry-Howard对应理论为LCTQ演算构造了相应的LCTQ标号自然演绎系统,从而提供了句法演算到语义计算的转换方式,为时态查询语句的语义分析提供相关接口。在下一步工作中,将主要研究类型演算λ-演算在时态查询中的语义演算和推理,并将其作为时态查询的语义机理论基础,建立相应的原型系统或直接在TempDB[5]上进行验证。
参考文献:
[1] CHOMICKI J, SAAKE G. Logics for databases and information systems: Temporal logic information system [M]. Boston/Dordrecht/London:Kluwer Academic Publishers, 1998.
[2] GABBAY D M, HODKINSON I , REYNOLDS M. Temporal logic: Mathematical foundations and computational aspects [M]. Oxford :Oxford University Press, 1994.
[3] LAMBEK J. The mathematics of sentence structure [J].Amer Math Monthly , 1958,65:154-170.
[4] BARENDEGT H P. The lambda calculus its syntax and semantics [J]. Studies in Logic and The foundations of Mathematics, 2004,103(6).
[5] http://www.cosoft.sysu.edu.cn/TempDB/index.htm, [2008].
[6] CURRY H B. Some logic aspects of grammatical structure [C]// JAKOBSON R. Stucture of language and its mathematical aspects. AMS, Providence, RI.
[7] HOWARD W.The formulae-as-types notion of construction [M].Manuscript, Published in Seldin and Hindley , 1980.
[8] RAO J H, KÜNGAS P. Logic-based web services composition from service description to process model [C]//In 2ndIntl. Conference on Web Services,2004.
[9] UUSTALU T, VENE V, The essence of dataflow programming [C]// In 3rd Asian Symp. on Programming Languages and Systems, APLAS’05, Number 3780 in Lect. Notes Comp Sci, 2005.
[10] HAJEK P. Metamathematics of fuzzy logic [C]//Trends in Logic 4. Kluwer, 1998.
