基于凸包的棋盘格角点自动识别与定位方法*
2009-05-08熊会元宗志坚陈承鹤
熊会元,宗志坚,余 志,陈承鹤
(中山大学工学院, 广东 广州 510275)
基于棋盘格的摄像机标定中,角点提取的精度与物像坐标的匹配是该算法的重要环节。现有角点提取方法可分为三类[1]:一是根据图像边缘特征,由边缘夹角[2]或曲率[3]来判断是否为角点;二是利用图像的灰度信息,如Susan算法[4];三是利用图像的灰度变化率,如Harris算法[5]。Schmid等[6]认为, Harris算法是目前最好的一种方法。该方法使用图像的一阶差分,计算每个像素的平均平方梯度矩阵,通过特征值分析得出角点的响应;不受摄像机姿态、光照、噪声等影响,具有效率高和较强的稳定性及鲁棒性。 但该算法的不足是提取的精度只有像素级,角点集包含外圈角点与格单元边缘上的伪点(图1所示绿色箭头所指),且点集中角点排序混乱。这样标定时,需手动完成角点像与物坐标匹配。
本文在Harris算法基础上,利用棋盘格内角点的对称性,设计对称算子,剔除外圈角点与伪角点。在此基础上,应用角点处灰度梯度算法,获取棋盘格亚像素角点。最后,在角点集中应用凸包算法分层识别并自动定位角点,实现角点物与像坐标的自动匹配,进而可实现摄像机精确快速标定。

图1 Harris 提取角点图
1 棋盘格内部角点识别与亚像素提取
1.1 基于对称算子的内部角点识别
Harris提取的角点集中,外圈角点受边界环境影响,角点提取的精度不高,不易作为标定点,因而应从点集中剔除。从棋盘格布局中可以看出,棋盘格内部角点具有以角点为中心,周围的灰度分布具有对称性特点;而外圈角点与格单元边缘上伪角点则不具备,据此原理定义如下式的对称算子[7]:
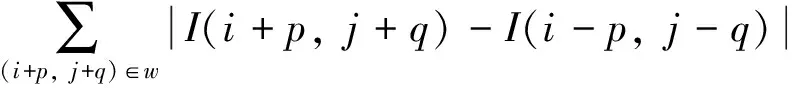
(1)
其中,I(i,j)为角点(i,j)处的灰度值,w为以(i,j)为中心的窗口,可根据图像中棋盘格单元大小设定,n为w中角点对称对的数量。
可通过设定cs的域值来区分角点是否为内部角点,其中小于域值的角点则认为是内部角点。图2为w取15×7,cs域值取65,对图1中棋盘格进行的识别结果图。
1.2 亚像素角点精确提取
为得到更高的角点精度,在Harris算法提取角点后,利用角点处灰度梯度获得亚像素级角点精度。文献[8]提到两种算法,其中基于灰度梯度的算法精度更高,应用较广,其原理如下:
设Harris算法提取的角点为p,则p指向领域内任意一点qi的向量都与qi的灰度梯度垂直。其表达式如下:

图2 应用对称算子识别内部角点图
(2)
2 基于凸包的角点分层识别与自动定位
摄像机标定的另一个环节是棋盘格角点的空间坐标与图像坐标的匹配。文献[9]应用平行线共灭点的原理,先确定中心格四角点,作直线求灭点,后由灭点与角点的距离来排序,依次确定其他栅格线上角点;文献[10]提出由中心角点出发,以图像x与y方向的动态增量dx与dy来预测和递推其他角点;上述算法受摄像机畸变影响较大,操作较复杂。由于棋盘格角点具有栅格排列与分层排列的特征,作者发现凸包算法能很好的识别与定位角点集中外层凸点;在凸包中,应用凸度识别并定位转角点,进而可识别与定位整个棋盘格角点。
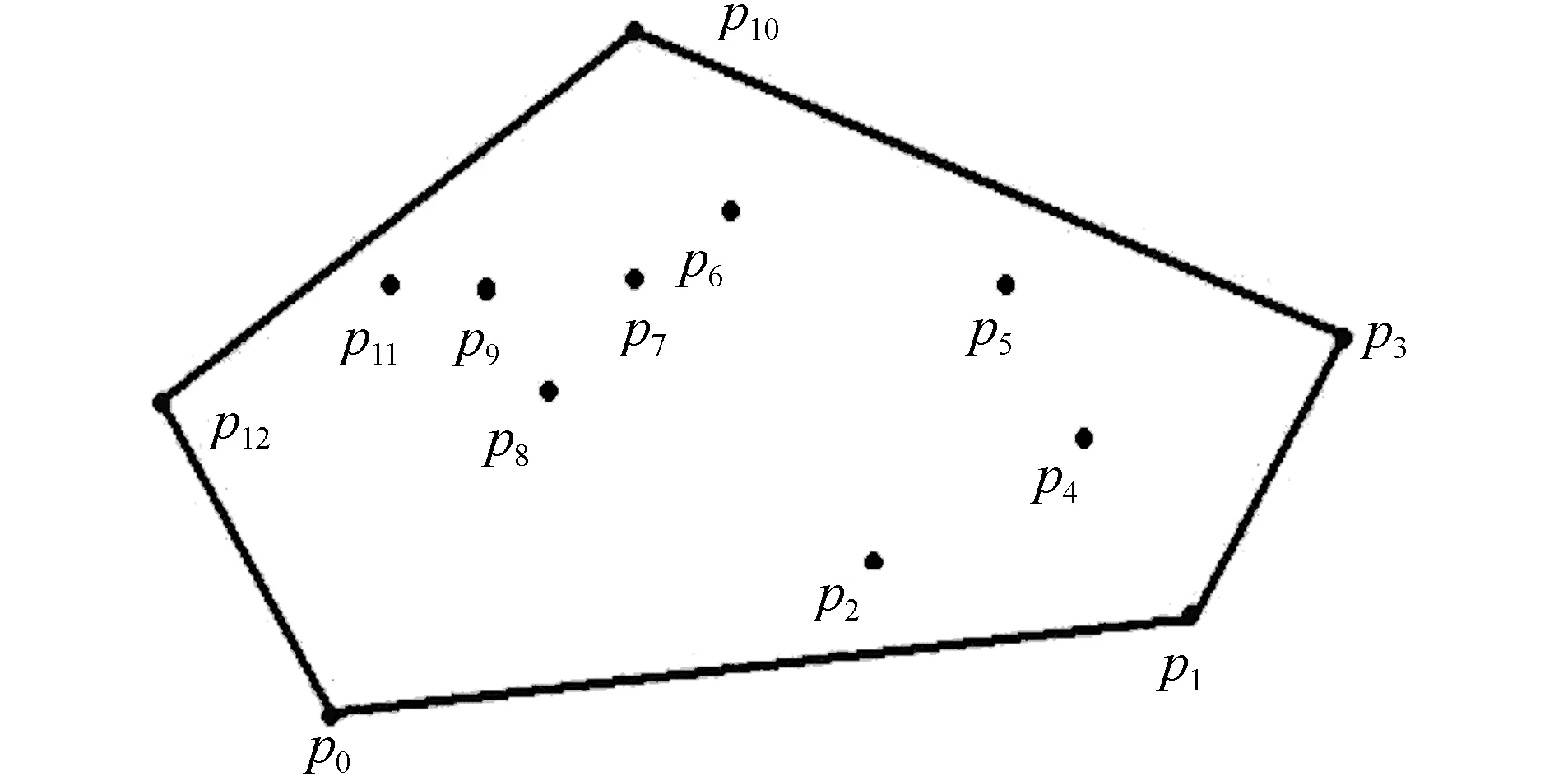
图3 凸包概念图
2.1 凸包的概念
平面点集的凸包定义为对平面上一个点集S,或一个多边形P,其凸包是指包含S或P的最小凸多边形。如下图中线段表示的多边形就是点集S={p0,p1,...,p12}的凸包。
定义1 设P为逆时针排序的凸多边形,其顶点的序列为{p0,p1,...pn-1},计T(P)为P的凸包,L(pi,pi+1)为顶点pi与pi+1的直线连接,TL(p0,pn-1)={L(p0,p1),…,L(pi-1,pi),…,L(pn-1,p0)}为凸包T(P)的直线集。

2.2 角点分层识别与自动排序
基于凸包的角点分层识别与自动排序包括角点集凸包的识别、凸包中的四个转角点识别与定位、同层角点的全识别与排序,以及角点全识别与排序等四个步骤。具体如下:
步骤一角点集凸包的识别
① 设Q0为m×n棋盘格角点的点集,取点p0(p0∈Q0且p0的x坐标最小,如有多个相等的最小值,则取其中y坐标最小的点);
② 以p0为中心,计算pi(pi∈(Q0-p0),i=1,...,m×n-1)相对于p0的极角,并以逆时针方向对极角排序,若极角相等,取离p0最远的点,则可得点集P(P={p0,...,pi,...,pr},其中r≤m×n-1);

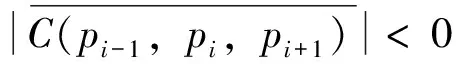

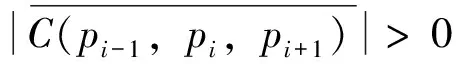
最后得到点集P={p0,...,pi,...,pk}(其中k≤r)所构成的多边形即为点集Q0的凸包T(P)。图4为应用本算法获得图2棋盘格点集的凸包图,由9个顶点组成。
步骤二凸包中棋盘格转角点识别与定位

② 求p0、p1、p2与p3的质心pc(x,y);
,
(3)


图4 棋盘格角点集凸包
步骤三同层角点的识别与排序
依次取凸包T′(P)直线集上直线L(pi,pi+1)(L(pi,pi+1)∈T′L(p0,pk);i=0,1,…,k),任取角点ql∈(Q0-P′)(l=0,1,...,m×n-1-k),求到直线L(pi,pi+1)的垂足fl与距离dl。设判断点在直线上的距离域值为εd,若dl≤εd且fl在直线段L(pi,pi+1)的pi与pi+1点之间,则认为点ql为直线L(pi,pi+1)上的点,并将ql按|pi-ql|距离由近至远的次序插入点集P′,遍历T′(P)上的直线集后可得以左上角点p0为起始点,逆时针存储的棋盘格同层角点的点序集P′(P′={p0,...,pi,ql,pi+1,...,pk})。
步骤四角点的全识别与排序


图5 按凸包次序排序图

图6 行列次序排序图
3 实验与结果分析
用Visual C++6.0编程实现了上述算法,用图7示数控实验平台,采用Watec 902B摄像机,f=25 mm镜头,拍摄15位置棋盘格图像(见图8),用本文算法完成角点精确提取与分层识别排序,用Zhang[11]完成标定;为进行对比实验,同时应用经典的基于Matlab摄像机标定程序[12],实现角点手动提取与定位,并标定,其标定对比结果如表1。

图7 实验图
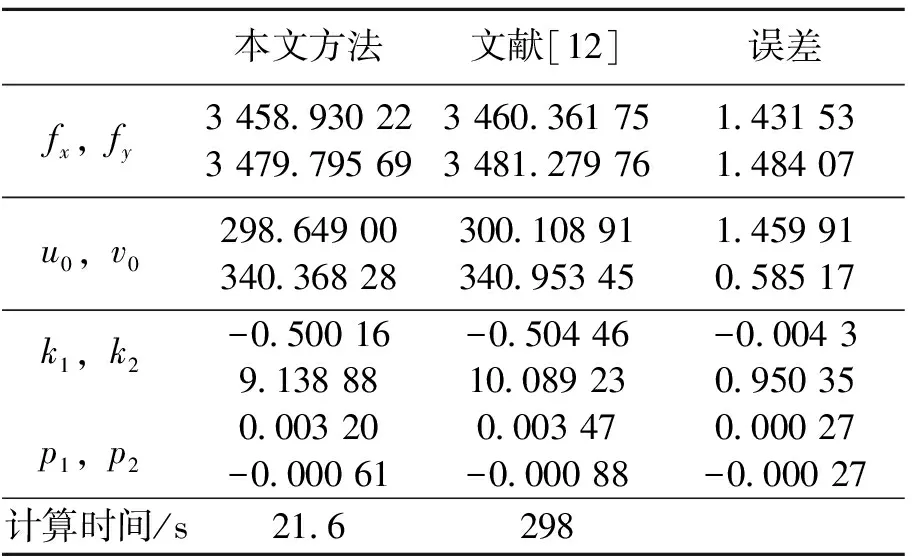
表1 对比实验结果表

图8 拍摄15位置标定图像
由上述实验可以看出,两种方法标定结果焦距fx,fy,主点u0,v0以及畸变系数(k1,k2,p1,p2)十分接近,误差较小。但本文方法可全自动实现,整个标定时间仅为21.6 s,而文献[12]需要手动提取,所需时间需要298 s。
4 结 语
本文应用Harris算子与基于角点处灰度梯度方法提取棋盘格角点,角点精度达亚像素。采用对称算子剔除棋盘格外圈角点与伪角点,实现棋盘格内角点的识别方法有效。提出的基于凸包的棋盘格角点的分层识别与自动定位方法可快速自动地实现物像坐标的匹配,进而实现摄像机自动标定。实验结果证明了方法的正确性与可靠性,适用于摄像机在线自标定。
参考文献:
[1] 张兆伟,赵字明,胡福乔,等. 基于样条小波的增强算法在角点提取中的应用[J].计算机工程与应用,2006,15:56-58.
ZHANG Z W,ZHAO Y M, HU F Q,et al .Corner extraction based on spline wavelet enhancement[J].Computer Engineering and Applications,2006, 15:56-58.
[2] HSIN T, HU W C. A rotationally invariant two-phase scheme for corner detection [J]. Pattern Recognition, 1996,28(5):819-829.
[3] MEDIONI G, YASUMOTO Y. Corner detection and curve representation using cubic B-spline[J]. Computer Vision Graphics Image Process, 1987, 39(3):267-278.
[4] SMITH S, BRANDY J M. SUSAN—a new approach to low level image processing[J]. Journal of Computer Vision,1997, 23(1): 45-78.
[5] HARRIS C, STEPHENS M.A combined corner and edge detector[C].Proceedings of the Fourth Alvey Vision Conference, Manchester, England, 1988: 147-151.
[6] SCHIMID C, MOHR R, BAUCKHAGE C. Evaluation of interest point detectors [J].International Journal of Computer Vision, 2000, 37(2): 151-172.
[7] 刘阳成,朱枫. 一种新的棋盘格图像角点检测算法[J].中国图象图形学报,2006,11(5):656-660.
LIU Y C, ZHU F. A new algorithm for X-corner detection[J]. Journal of Image and Graphics,2006,11(5):656-660.
[8] 梁志敏,高洪明.摄像机标定中亚像素级角点检测算法[J].焊接学报,2006,27(2):102-105.
LIANG Z M,GGO H M. Sub-pixels corner detection for cam era calibration[J]. Transactions of the China Welding Institution, 2006,27(2):102-105.
[9] 王忠石,徐心和. 棋盘格模版的自动识别与定位[J].中国图象图形学报,2007,12(4):618-622.
WANG Z S, XU X H. Auto-recognition and auto-location of the checkerboard pattern corner[J]. Journal of Image and Graphics,2007,12(4):618-622.
[10] 刘群根. 基于梯度与对称度提取棋盘格角点及角点递推定位[J]. 测控技术,2008,27(1):7-9.
LIU Q G. Extracting checkerboard corners based on gradient& symmetry and locating with Iteration[J]. Measurement& Control Technology, 2008,27(1):7-9.
[11] ZHANG Z.A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.
[12] BOUGUET J Y.Camera calibration toolbox for Matlab [EB/OL]. http://www.vision.caltech.edu/bouguetj/calib_doc/htmls/example.html.
