“鸡兔同笼”问题的解法探讨
2009-04-14李树清
李树清
摘 要:“鸡兔同笼”问题是我国古代数学趣题之一,也是当今小学数学课外活动专题之一。在小学阶段,应结合小学生已有的知识基础和生活经验,对“鸡兔同笼”类数学题进行多角度的解法探讨。
关键词:小学数学;鸡兔同笼问题;解法探讨
中图分类号:G623.5 文献标识码:A 文章编号:1009-010X(2009)03-0050-02
“鸡兔同笼”问题是我国古代趣题之一。大约在1500年前,《孙子算经》中就记载了这个有趣的问题。书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话用现代数学语言说意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。求笼中鸡和兔各有几只?
这就是鸡兔同笼问题,通常情况下,人们喜欢用假设法来解答此类问题。假设法是一种常用的解题方法,用假设思想解应用题,首先要根据题意正确地判断应该怎么假设(一般可假设要求的两个或几个未知量相等、或者假设要求的两个未知量是同一种量);其次,要根据所作的假设,注意到数量关系发生了什么变化,怎样从所给的条件与变化了的数量关系的比较中做出适当的调整,从而找到正确的答案。
解法一:假设他们全是鸡,根据鸡兔的总数就可以算出在假设条件下一共有几只脚,把这样得到的脚数与题中给出的脚数相比较,看看差多少,每差两只脚就说明有一只兔,将所差的脚数除以二,就可以先算出一共有多少只兔,进而算出有多少只鸡。
兔子的只数:(94-35×2)÷(4-2)=12(只)
鸡的只数:35-12=23(只)
解法二:假设它们全是兔,则应有4×35=140(只)脚,现在有94只脚,少了140-94=46(只)脚,原因是把鸡全都假设成了兔子,一只鸡比一只兔子少2只脚,所以,鸡的只数就可以求出来了。
鸡的只数:(4×35-94)÷(4-2)=23(只)
兔子的只数:35-23=12(只)
解法三:运用假设法解题逻辑思维性较强、比较抽象。我们还可以运用列表枚举法来解答此类问题。
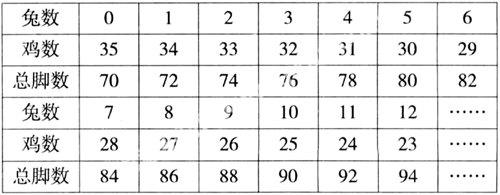
从上表的枚举可以看出兔子有12只,鸡有23只。
解法四:列表枚举法虽然形象、易懂,但很麻烦,运用方程法来解答更简略些。
1) 解:设兔子有x只,则鸡有35-x只,则兔脚有4x只,鸡脚有2×(35-x)只,依据题意得:
4x+2×(35-x)=94
解得x=12 35-12=23(只)
所以兔子有12只,鸡有23只。
2) 解:设鸡有x只,则兔有35-x只,则鸡脚有2x只,兔脚有4×(35-x)只,依据题意得:
2x+4×(35-x)=94
解得 x=2335-23=12(只)
所以鸡有23只,兔子有12只。
解法五:鸡兔同笼问题一般都是用以上几种解法来解答,思维的角度是用算术、方程,能否把鸡兔同笼问题转变成一道更加直观、形象、容易解答的几何图形题呢?我们来看这样一个图形:

图形中AB=35,BC=2,AF=4,图形AHEF和图形HBCD的面积和为94,求AH=?HB=?
这道题就是鸡兔同笼问题的一种几何图形表达形式,AH为兔子的只数,HB为鸡的只数,AB表示鸡兔共有35只,BC=2表示每只鸡有2只脚,AF=4表示每只兔有4只脚,图形AHEF和图形HBCD总面积为94表示鸡兔共有94只脚。最后求AH=?即兔有多少只?HB=?即鸡有多少只?
这道题巧妙地应用了长方形的面积=长×宽。
兔的只数×每只兔4只脚 + 鸡的只数×每只鸡2只脚 = 鸡兔共有94只脚
AH × AF + HB × BC = 94
长方形AHEF的面积 + 长方形HBCD的面积= 图形总面积为94
延长CD交AF与G,在长方形ABCG中,已知AB的长度和BC的长度,则长方形ABCG的面积很容易求出,长方形AHEF和长方形HBCD的面积和已知,减去长方形ABCG的面积,那么可以求出长方形GDEF的面积,由于GF=GA=BC=2,在长方形GDEF中,已知面积和GF的边长,EF可以求出,EF=AH,已知AB的长度,则HB也可以求出,这样,AH即兔有多少只,HB即鸡有多少只即知。
解:在图形中线段AH表示兔有多少只,HB表示鸡有多少只,总面积94表示鸡兔共有94只脚,BC表示每只鸡有2只脚,AF表示每只兔有4只脚,延长CD交AF与G,在长方形ABCG中,AB=35,BC=2,则长方形ABCG的面积:35×2=70,长方形AHEF和长方形HBCD的面积和为94,则长方形GDEF的面积的面积:94-70=24。由于GF=GA=BC=2,所以EF=24÷2=12,EF=AH,则AH=12,即兔有12只,HB=35-12=23,即鸡有23只。
对于要同时考虑两个因素的类似“鸡兔同笼”问题的一些应用题,如果用长方形的长和宽分别表示两个不同的因素,画出长方形来,再利用长方形的面积进行分析,往往解题思路十分快捷。
“鸡兔同笼”问题的解法是多种多样的,从不同的思维角度往往能探索出更新的解法,从而满足不同学生的发展需要,大家不妨一试。
【责任编辑 高洁】
