尺度效应对全附体潜艇阻力数值计算结果的影响

操盛文 吴方良

1海军装备部驻武汉地区军事代表局，湖北 武汉430064

2中国舰船研究设计中心，湖北武汉430064

尺度效应对全附体潜艇阻力数值计算结果的影响

操盛文1吴方良2

1海军装备部驻武汉地区军事代表局，湖北 武汉430064

2中国舰船研究设计中心，湖北武汉430064

采用数值计算方法对SUBOFF潜艇的全附体模型进行三维粘性流场数值模拟，将雷诺数为1.2×107时的计算结果同试验结果进行比较，验证了计算方法的可靠性；采用不同数量的网格分别对不同尺度的SUBOFF模型在高雷诺数条件下的流场进行数值模拟，研究网格数量和艇体主尺度大小对高雷诺数条件下潜艇阻力计算结果的影响，通过对计算结果的分析，获得了尺度效应和网格数量对潜艇阻力数值计算结果的影响规律。

潜艇阻力；高雷诺数；粘性流场；数值计算

1 引言

随着计算机硬件和软件技术的发展，潜艇学术界和工程界迫切需要对潜艇在高雷诺数条件下的水动力特性进行数值模拟和试验研究，由于目前在实验室无法对潜艇进行高雷诺数 （实艇雷诺数）条件下的水动力试验，建立专门的潜艇水下测速场是一项费用需求很大的工程，根据潜艇的航速来反推潜艇航行时的总阻力也只能精确到一定的水平。因此，采用数值方法对潜艇在实艇雷诺数条件下的流场进行模拟有着非常重要的意义。但是，利用数值计算对高雷诺数条件下潜艇流场进行模拟，要求计算网格的数量大幅度增加，需要数百万乃至数千万的网格，才有可能对实艇雷诺数条件下的流场进行计算。过去由于计算条件，特别是计算机硬件条件的限制，针对潜艇在高雷诺数条件下流场和阻力的数值计算很少见到。国内的一些学者［1，2］针对潜艇在低雷诺数条件下的粘性流体数值计算方法进行了探讨，但在高雷诺数领域的数值计算研究鲜有报道。以前对潜艇的流场进行数值模拟和试验研究，主要集中在模型尺度的雷诺数计算，即在Re＝107左右条件下进行的［3，4］文献［5］采用数值计算和试验研究了高雷诺数条件下尺度效应引起的潜艇阻力变化。世界上许多军事发达国家针对该雷诺数附近潜艇流场的数值计算和测试领域做了大量细致深入的工作，许多国家的船池，尤其是美国的Tailor船池以SUBOFF模型作为标准模型进行系统的水动力与流场的测量试验工作，提供了包括速度、压力、摩擦阻力、雷诺应力和阻力等大量的水动力和流场数据［6-8］，这为全世界的计算流体力学研究者提供了一个用来验证数值计算程序的交流平台。

本文利用中国舰船研究中心的大型计算工作站，采用千万级网格针对潜艇在高雷诺数下的流场开展了数值计算。为了研究计算网格的数量对计算结果的影响，本文分别采用不同网格数量的计算模型对高雷诺数条件下的潜艇流场进行了数值模拟，通过对比计算结果，分析了计算网格数量对高雷诺数条件下计算结果的影响。同时研究了在同一雷诺数条件下，艇体尺度的大小对计算结果的影响。

2 潜艇三维流场计算的数学模型

2.1 计算对象

本文对SUBOFF全附体模型的三维粘性流场进行模拟计算。在研究过程中，为了研究在同一高雷诺数条件下，艇体尺度对计算结果的影响，本文将模型的尺度放大15倍。放大以后的模型为SUBOFFG，将该模型在同样的雷诺数条件下重新进行数值模拟，以比较两种条件下的计算结果差异。SUBOFF模型放大前后的主尺度见表1。

表1 SUBOFF模型放大前后的主尺度

2.2 控制方程

不可压缩流体的连续性方程：

2.3 湍流模型

本文计算潜艇在深水下航行时的阻力，不考虑高速运行时的空泡特性。根据对Reynolds应力做出的假定或处理方式不同，目前常用的湍流模型有：标准k－ε湍流模型、RNG k－ε湍流模型、Realizable k－ε模型、k－ω湍流模型、Reynolds应力方程模型［9］等。其中，标准k－ε湍流模型、RNG k－ε湍流模型、Realizable k－ε模型都是针对充分发展的湍流才有效，即这3个模型均是高Re数的湍流模型。但是标准k－ε湍流模型，对于时均应变率特别大的情形，有可能导致负的正应力。而Realizable k－ε模型则是克服了这一缺点发展起来的。作者采用不同的湍流模型针对全附体潜艇的三维粘性流场进行了系列对比计算，详细的计算结果将另文专述。根据计算结果，对于全附体潜艇在高雷诺数条件下的流场计算，应用Realizable k－ε湍流模型进行数值模拟效果最好。下面仅给出该湍流模型的数学表达式，详细的推导过程和各参数的选取可参考文献［9，10］。对于壁面区的流动采用壁面函数法（wall functions）进行处理。

在Realizable k－ε模型中，关于k和ε的输运方程如下：

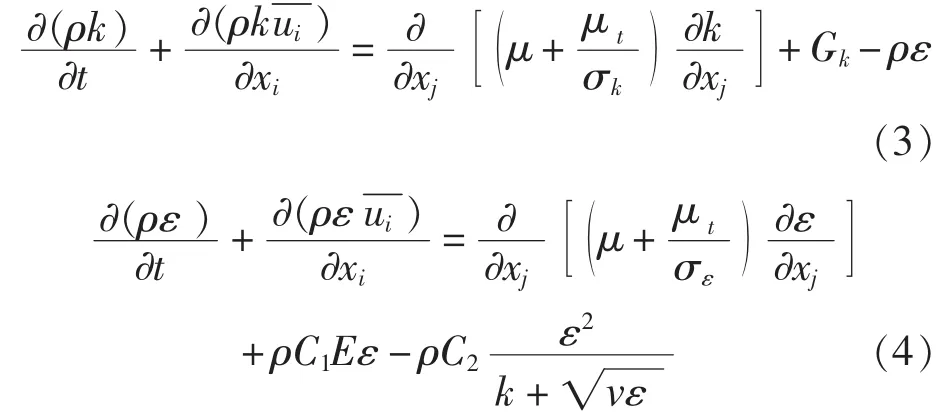
2.4 数值计算方法

采用有限体积法离散控制方程和湍流模式。对于压力方程、动量方程、湍流方程、雷诺应力方程，均采用二阶迎风格式进行离散，压力速度耦合迭代采用Simplec算法。

2.5 边界条件

计算流场域的边界由进流边界、出流边界、壁面边界和控制域边界组成。本文计算区域模型如图1。

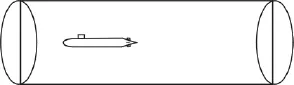
图1 全附体模型计算区域示意图

进流边界条件：取在回转体艏前方5倍艇体直径处。采用速度进口边界条件。u＝U0，v=w=0。其中U0为来流速度，对SUBOFF模型和SUBOFFG模型的计算来流速度及其对应的雷诺数见表2。

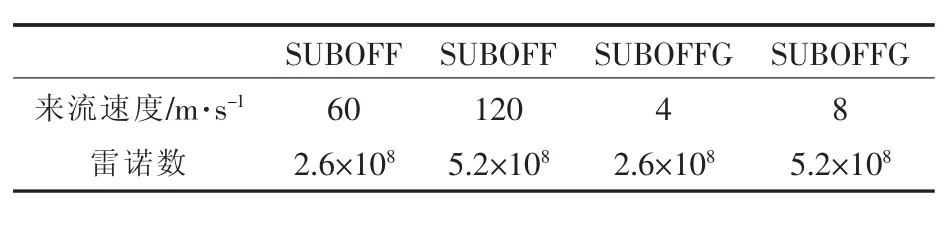
表2 两个计算模型的来流速度及其对应的雷诺数

出流边界条件：取在回转体后方距艉端点15倍艇体直径处，压力出流边界条件。

壁面边界条件：采用无滑移边界条件。

控制域边界条件：取5倍艇体最大直径。速度为没有受到扰动的边界条件。

2.6 计算网格

本计算所有的计算模型均采用六面体结构性网格，采用多块贴体网格耦合生成方法，在艇体周围划分出一个区域，生成C型网格，其它区域则生成H型网格，并对艇体附近的网格进行加密处理。

图1为本文所用的计算模型中的一个模型艇体表面的网格，图2为模型对称面上的网格。在所有的各计算模型中，采用同样的网格形式，不同网格数量的模型只是网格的密度不同。

图2 全附体模型表面网格

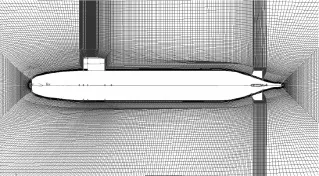
图3 全附体模型对称面网格

2.7 计算模型和方法在Re＝1.2×107条件下的验证

文献［7］针对潜艇在Re＝1.2×107条件下的流场进行了数值模拟，并研究了计算网格的数量和形式对计算结果的影响。根据文献［7］的计算结果，当采用结构网格，且网格数目达到50万的时候，计算结果就比较稳定且接近于试验结果。本文利用165万网格模型，分别对SUBOFF的主艇体模型和全附体模型进行了计算，来流速度为U0，保证以潜艇总长为特征长度的雷诺数Re＝1.2× 107，并将计算结果同试验结果［7］进行了比较。比较结果见图4～图5。从计算结果和试验结果的比较可以看出，该网格模型和计算模型具有很高的计算精度。

图4为主艇体纵中剖面线上半部分压力系数的纵向分布曲线，图5为潜艇纵中剖面线上半部分壁面剪应力系数的纵向分布曲线。

图4 主艇体纵中剖面上半部分压力系数

图5 主艇体纵中剖面上半部分摩擦阻力系数

本文中，坐标原点为艇首端点，设定纵中剖面与基面的交线为X轴 （横坐标），向艇尾为正方向；纵中剖面与舯截面的交线为Z轴（竖坐标），向上为正方向；舯截面与基面的交线为Y轴（纵坐标），向右舷为正方向。图中，x为艇体表面点的X坐标值，L为艇体长度。各符号的定义如下：

压力系数定义为CP＝2（p－p0）／ρU20；壁面剪应力系数Cτ＝2Tw／ρU20；压阻力系数CR＝RR／（0.5·ρV2）；摩擦阻力系数Cf＝Rf／（0.5·ρV2）；总阻力系数Ct＝Rt／（0.5·ρV2）。p为艇体表面各点的压力；Tw为壁面各点剪应力；RR为潜艇所受的粘压阻力；V为来流速度；Rf为潜艇所受的摩擦阻力；Rt为潜艇所受的总阻力。

3 计算结果与讨论

本文同时针对Re＝2.6×108，在保证总网格数为1 010万以及网格结构不变的条件下，通过改变边界层网格的厚度，研究壁面 Y＋函数对阻力计算结果的影响。计算模型艇体长度均为65.341 5 m，来流速度为4 m／s，计算模型的参数及计算结果见表3，艇体表面纵中剖面的Y＋分布曲线见图6。△yp表示近壁面节点P到固壁的距离。根据计算结果可以看出，艇体表面的Y＋值越小，计算结果越小。计算结果之间的差别约占总阻力的7%。因此本文中各模型的艇体表面网格均为0.5 mm。

表3 不同壁面网格厚度模型的参数及计算结果

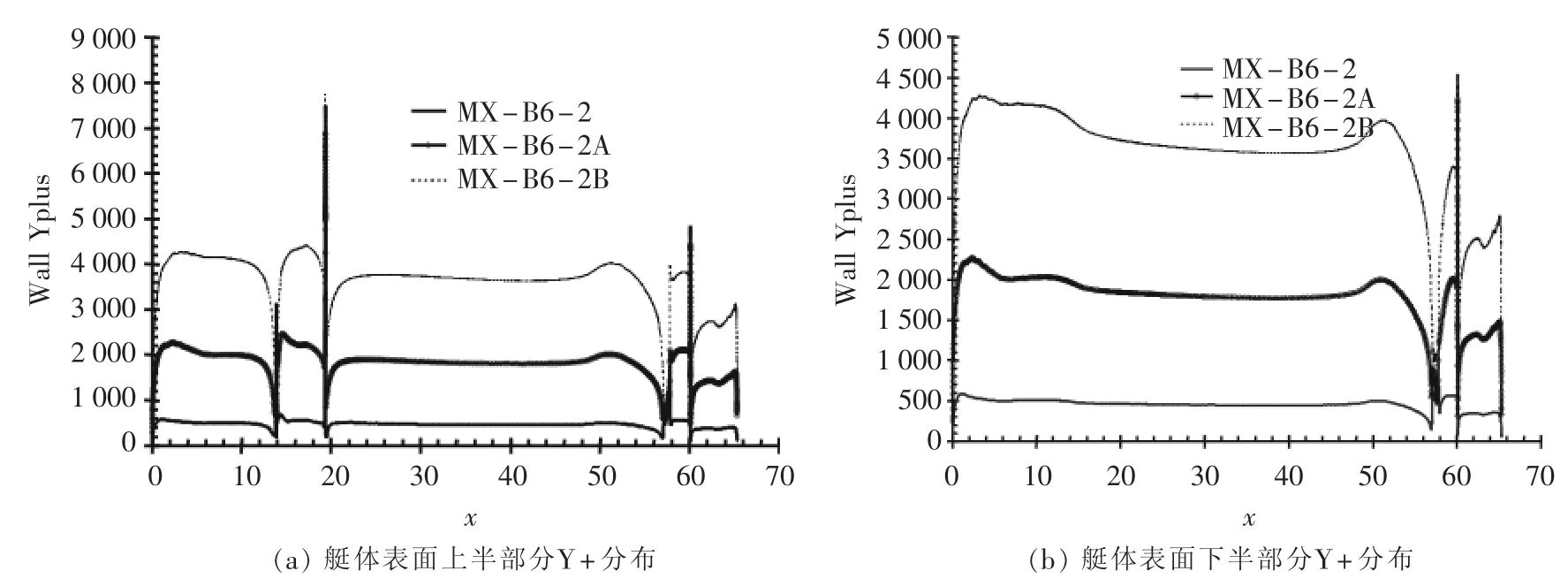
图6 艇体表面纵中剖面的Y＋分布曲线

为了研究计算网格的数量对计算结果的影响，本文分别采用165万、1 010万等6种不同的网格数，对雷诺数为Re＝2.6×108、Re＝5.2×108条件下不同艇体尺度总共24种情况进行了计算。各计算模型的网格数、主尺度及计算结果等具体参数见表4，表中最后一列为采用ITTC57公式计算的摩擦阻力系数。图7为MX－B6－2计算的艇体表面压力分布，图8为不同雷诺数、不同艇体长度条件下总阻力系数随网格数量变化的曲线，图9为不同雷诺数、不同艇体长度条件下粘压阻力系数随网格数量变化的曲线，图10为不同雷诺数、不同艇体长度条件下摩擦阻力系数随网格数量变化的曲线。

分析数值计算结果，可以得出以下几点规律：

1）为了研究适合于潜艇在高雷诺数条件下的数值计算方法，本文通过系列地变换艇体尺度和计算域网络数目，对潜艇在高雷诺数条件下的粘性流场进行了数值模拟，计算结果表明：采用小尺度艇体，高来流速度的状态并不适合对潜艇在高雷诺数条件下的流场进行数值模拟。

图7 艇体表面等压线图

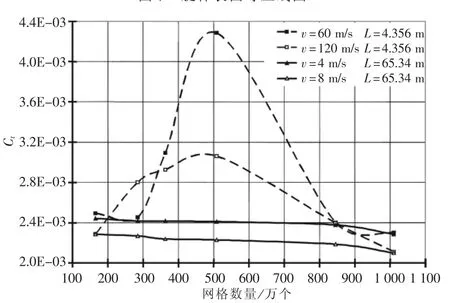
图8 总阻力系数随网格数量变化的曲线

2）对于Re＞108的潜艇阻力计算，在同样的雷诺数条件下，采用大尺度艇体、低来流速度的计算结果比较稳定，当网格数大于400万以后，网格数量的增加对计算结果的影响很小。

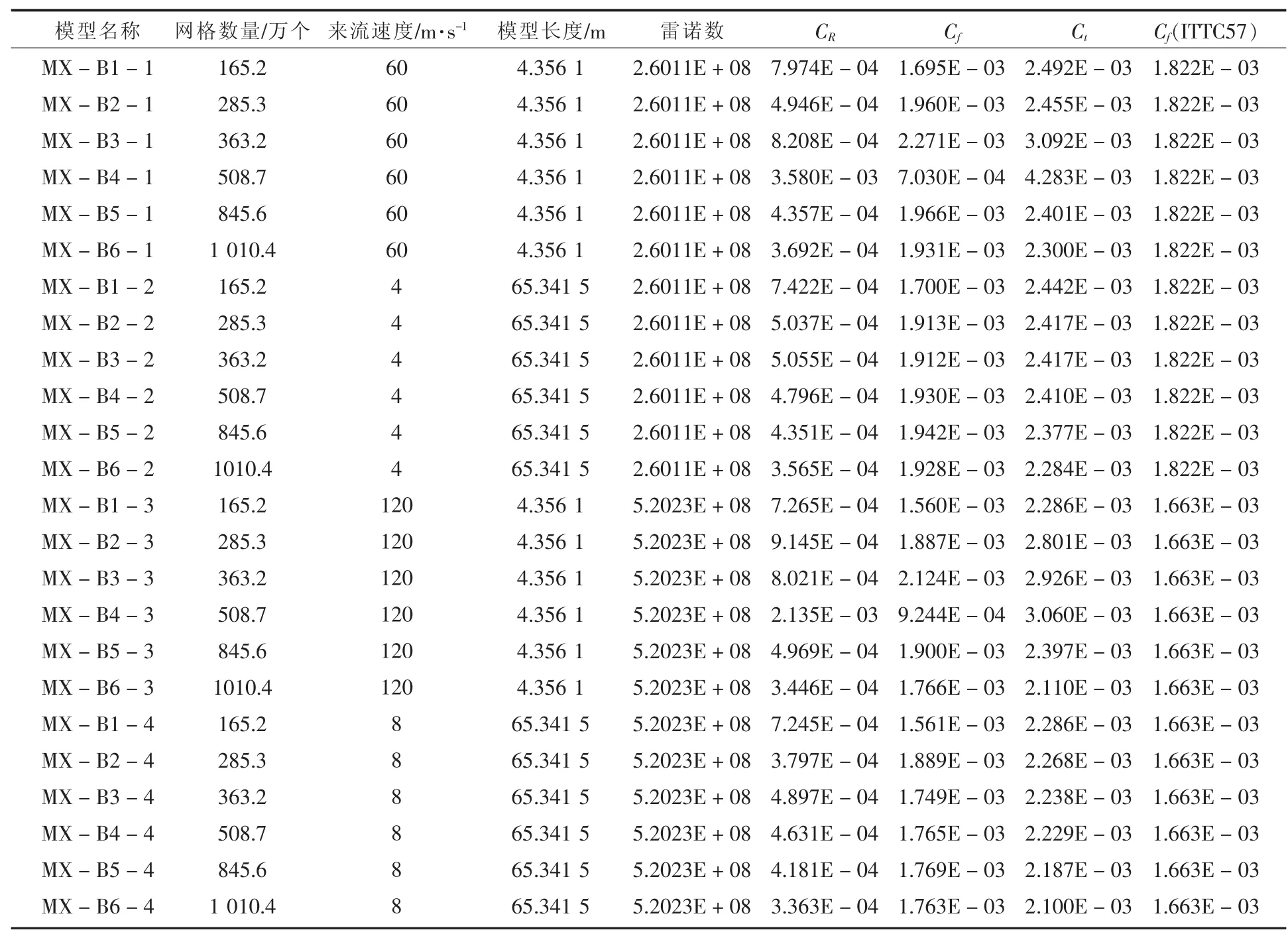
表4 各计算模型的参数及计算结果

图9 粘压阻力系数随网格数量变化的曲线

图10 摩擦阻力系数随网格数量变化的曲线

3）本文对潜艇在高雷诺数条件下的计算结果虽然没有得到试验的验证，但是根据表4、图9和图10可以看出，Re＝2.6×108和Re＝5.2×108时的粘压阻力系数基本相同；Re＝5.2×108时的摩擦阻力系数低于Re＝2.6×108的摩擦阻力。本文计算的摩擦阻力系数同ITTC57公式计算的摩擦阻力系数也非常接近。这在规律上同理论分析的结果是完全一致的，说明本文针对潜艇在高雷诺数条件下的流场计算结果具有较好的准确性和可靠性。

4）针对高雷诺数条件下潜艇粘性流场的研究过去发表的文献不多，在现代计算机硬件高速发展的条件下，从工程师研制角度更进一步系统地开展该领域的研究工作，以完善高雷诺数条件下的计算理论和方法是很有必要的。

［1］赵峰，周连第.潜艇含指挥台附体区域周围粘性流场的多块耦合计算 ［J］.水动力学研究与进展A辑，1996，11（4）：448－458.

［2］张楠，沈泓萃，姚惠之.潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究［J］.船舶力学，2005，9（1）：1－13.

［3］BENSOW R E，et al.Large eddy simulation of the viscous flow around submarine hulls［A］.25thsymposium on Naval Hydrodynamics ［C］， StJohn’s， Newfoundland and Labrador，Canada，2004.

［5］BULL P，WATSON S.The scaling of high Reynolds number viscous flow predictions for appended submarine geometries ［A］.Proceedings of 22ndSymposium on Naval Hydrodynamics［C］，Washington，USA，1998.

［4］YANG C I，BETHESDA.Numerical simulation of threedimensional viscous flow around a submersible body［C］.In： Proceedings of 5thInternational Conference on Numerical Ship Hydrodynamics，Hiroshima，Japan，1989.

［6］HUANG T，LIU H L，GROVES N et al.Measurements of flows over an axisymmetric body with various appendages in a wind tunnel：the DARPA SUBOFF experimental program ［C］.In：Proceeding of 19thSymposium on Naval Hydrodynamics，Seoul，Korea，1992.

［7］BULL P.The validation of CFD predictions of nominal wake for the SUBOFF fully appended geometry［C］.In：Proceedings of 21stSymposium on Naval Hydrodynamics，Trondheim，Norway，1996.

［8］Serge Toxopeus，Viscous－flow calculations for bare hull DARPA SUBOFF submarine at incidence［J］.International Shipbuilding Progress，2008（55）：227-251.

［9］王福军.计算流体动力学分析［M］.北京：清华大学出版社，2006.

［10］张兆顺，崔桂香，许春晓.湍流理论与模拟［M］.北京：清华大学出版社，2005.

Investigation of Scaling Effects on Numerical Computation of Submarine Resistance

Cao Sheng－wen1Wu Fang－liang2
1 Wuhan Representative Office of Chinese Navy Armament，Wuhan 430064，China 2 China Ship Development and Design Center，Wuhan 430064，China

The 3－D viscous flow around SUBOFF model with full appendages was simulated by numerical method.The measured and computed data with the Reynolds number of 1.2×107were compared to validate the reliability of the method.The flow around different scale of SUBOFF model at the large Reynolds number was simulated by different number meshs.As both the number of mesh and the main dimension of model had an effect on the CFD resistances of submarine，the results were analyzed and the rule that mesh number and scaling effects in numerical computation of submarine resistance is obtained.

total submerged resistance of submarine；large Reynolds number；viscous flow field；numerical computation

U674.76

：A

：1673－3185（2009）01－33－05

2008－11－12

操盛文（1956－），男，高级工程师。研究方向：船舶与海洋工程

吴方良（1975－），男，博士，博士后研究人员。研究方向：船舶工程。E-mail：wflcjh@163.com