水下圆柱壳冲击响应分析的有限元模型简化方法
2009-04-08孙占忠胡刚义张新宇黄国兵
孙占忠 胡刚义 张新宇 黄国兵
中国舰船研究设计中心,湖北 武汉430064
水下圆柱壳冲击响应分析的有限元模型简化方法
孙占忠 胡刚义 张新宇 黄国兵
中国舰船研究设计中心,湖北 武汉430064
基于显式非线性动力学分析程序ABAQUS,对水下圆柱壳受到水下爆炸冲击作用下的非线性动态响应进行研究。详细计算不同简化模型受到水下爆炸冲击波作用下的响应并与完整模型的结果进行对比。研究结果表明,用圆柱壳结构的部分模型代替完整模型,可以得到较为满意的计算结果。
模型;简化;水下爆炸;冲击响应
1 引言
舰船的抗冲击研究是振动领域比较热门的一个课题,但可应用于工程实际的研究成果还较少。目前,研究的热点集中在船体结构的冲击响应、舰船内部设备的冲击环境及对其进行有效的冲击隔离研究等方面,在各大高校和研究院所都有所研究。数值模拟分析在舰船的抗冲击研究中具有重要地位。为了取得良好的数值模拟结果,需要建立较准确的有限元模型。
通常对船体采用三种有限元模型:
1)全船船体梁模型;
2)全船三维模型;
3)船舶三维模型和梁模型相结合的整船混合有限元模型。
全船船体梁模型是将整船简化为沿一条直线的梁单元,其优点是划分的单元和节点数少,计算速度快,模型前处理工作量不大;缺点是不能反映内部结构的真实情况,无法分析船舶内部的薄弱环节。全船三维模型将船体离散成许多壳单元和梁单元的组集,其优点是能相对真实地反映船舶内部的情况,缺点是前处理工作量大,计算时间长。
文献[1,2]对船体尾部混合有限元模型的建立提出了有效的方法,并在实际工程应用中证实,说明这些方法对船体的振动分析有较好的适用性。然而冲击与振动不同,这些方法是否适用于冲击响应分析有待于进一步研究。本文对圆柱壳采用三维结构与一维梁混合有限元模型和全部三维模型进行对比分析,探讨混合模型对于抗冲击模拟的可行性和准确性。本文主要运用ABAQUS等有限元程序,对圆柱壳体、外部水体进行建模,并模拟爆炸冲击波,同时考虑流固耦合作用,计算冲击响应。
2 有限元建模
2.1 三维圆筒整体模型
以钢质圆筒为研究对象,其原始数据为:长L=10 m;直径R=1 m;筒体厚度0.028 m;两端盖板厚度为0.05 m;E=2.1×1011Pa;密度ρ=7 850 kg/m3;泊松比ε=0.3。用四边形壳单元模拟。壳体网格划分时,考虑到单元尺寸和时间步长对计算精度的影响,壳体网格尺寸取冲击波长[3](λ=θc)的1/6。
壳体外部水体需要包围整个圆筒,考虑到流固耦合的影响,流体模型范围取约为壳体半径的6倍时,附加质量与无限水域相比满足精度要求,即两端半球体半径为3 m,中部环形水体长度与圆筒长度相同。为了达到更好的精度,采用六面体声学单元模拟流体,对水体进行网格划分,由于水体内部表面与圆筒外表面存在流固耦合作用,水体内表面单元不能太大,否则引起壳体表面应力应变极不均匀,其值取决于冲击波长的大小。本模型取水体内部表面单元大小为λ/6,水体外表面单元大小为λ/3。
将圆柱壳体与水体模型组装在一起,并定义结构模型外表面与水体内表面间的流固耦合面(ABAQUS中并不要求两个耦合面间的节点重合),这样就完成了整个系统建模过程[4],系统模型如图1所示,为表示方便隐去上部流体单元。

图1 圆柱壳体及水体耦合模型
本文所用TNT炸药重量W=225 kg,爆炸点与入射点间距为R=13.6 m,则入射点的压力—时间函数如图2。
2.2 两种简化方案模型
采用以下两种方案。
方案1:取圆筒的前后1/3部分用梁模型简化与圆筒三维模型联结,联结方式为梁节点和筒体圆周上的单元连接,联结处采用运动耦合约束,且假设该圆周上单元的刚度很大(采用MPC刚性连接),从而保证联结剖面处的变形一致,见图3(a)。
方案2:采用局部圆筒结构,取总长度的1/3,见图3(b),即在方案1的基础上,抛弃前后的梁模型。
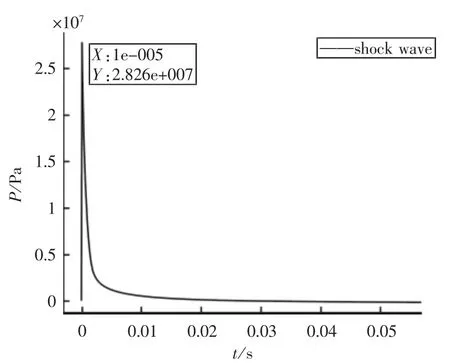
图2 冲击波压力—时间函数

图3 两种方案有限元模型
2.3ABAQUS软件的特殊梁模型
ABAQUS软件提供一种划分了网格的横剖面用于程序的梁分析并能给梁单元施加载荷。对于某些结构的响应和梁的响应相似,然而这些梁剖面的几何或这个剖面是由多种材料组成的原因,不能使用预先存在的梁单元库模拟。在这些方案中,划分网格的横剖面来模拟梁剖面并产生梁剖面属性适用于Timoshenko梁分析。产生的梁剖面属性包括轴向、弯曲、扭转和横向剪切刚度、质量、转动惯量和阻尼属性,还包括这个剖面的质心和剪切中心。产生典型梁剖面属性包含下列数据行,以本文使用的梁剖面为例:

需要划分网格截面结构的典型应用是船体的振荡分析,船体是由多种部件和多种材料组成的建筑。其他应用包括桨叶和机翼的翼型,分层的复合工字梁等。在ABAQUS中使用下列命令将简化的梁单元和三维立体结构进行运动耦合连接,并提供附连水质量。

3 基本理论
在目前的数值分析中,有限元法和边界元法均被采用。有限元法用来模拟壳体结构,边界元法用来模拟其周围的水介质。在结构分析中,采用VEC/DYNA3D程序[5],使用不同的壳体单元类型,其中包括Hughes和Liu以及Belytschko[6]等人采用的壳单元和厚壳单元,几乎得出了相同的结果。本文使用的钢材的弹塑性本构方程未考虑应变强化假设。
水作为声介质,用于距结构一定距离处爆炸物的传播媒介。壳结构和声学水介质之间的相互作用是通过双重渐进近似法(DAA)[7]的近似技术来模拟的。DAA技术使用边界元法来减少用于模拟声学介质所需要的单元数量。在计算条件较差时,DAA法得到了广泛的应用。但随着计算机技术的发展和精确的无反射边界条件的实现,采用经典的有限元法精确逼近求解流固耦合问题又重新具有了优势。
下面来分析流固耦合作用。结构的运动方程可以用如下的有限元法给出:
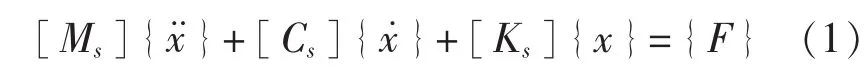
式中,[Ms]、[Cs]和[Ks]分别表示结构的质量、阻尼和刚度矩阵;{F}表示力矢量;{x}是节点位移矢量,并具有二阶时间导数。一部分力取决于流固耦合作用,一部分力取决于其他作用在结构上的外力。取决于流固耦合作用的力只发生在结构的湿表面上。因此,这个力矢量可以写为:
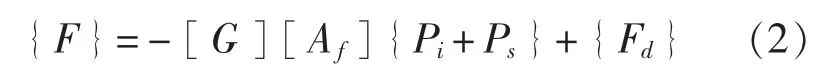
式中,[G]是流固耦合传递矩阵;[Af]是与流体网格有关的对角线面积矩阵;Pi和Ps分别是入射和散射压力,这里所说的散射压力是波浪理论中绕射压力和辐射压力的总和;{Fd}是作用于干结构上的力矢量。在方程(2)中,当给定一个爆炸载荷时,散射压力是未知的,入射压力是已知的。
为了得到散射压力值,下面方程是通过使用DAA理论和边界元技术一起得到的:

式中,[Mf]是流体质量矩阵;ρ和c是水密度和水中声速;{u˙s}是结构表面法线方向的散射波流体质点速度矢量。剩下的变量如上所述。流固耦合作用通过方程(2)联立方程(1)和(3)。散射波流体质点速度与结构速度有关,如方程(4)所示:
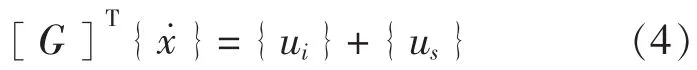
式中,T是转置矩阵的标志;i和s分别代表入射波和散射波。
方程(1)~(4)是完整的流固耦合表达式。方程(3)是精确的。在数值求解过程中引入一个增量,用交互求解的方法使方程求解时具有更好的稳定性[8]。基于以上数值方法理论,国外的科研机构和公司开发了一些通用计算软件。本文的计算采用基于声固耦合算法的ABAQUS软件。
4 结果对比分析
4.1 方案1结果分析
三维长圆筒整体模型与用特殊梁简化的混合模型进行比较分析。选取圆筒中心截面处4个典型节点加速度、位移曲线进行对比,如图4、图5所示。并对典型节点的冲击谱速度VS进行对比分析(表1)。

图4 典型节点加速度曲线对比
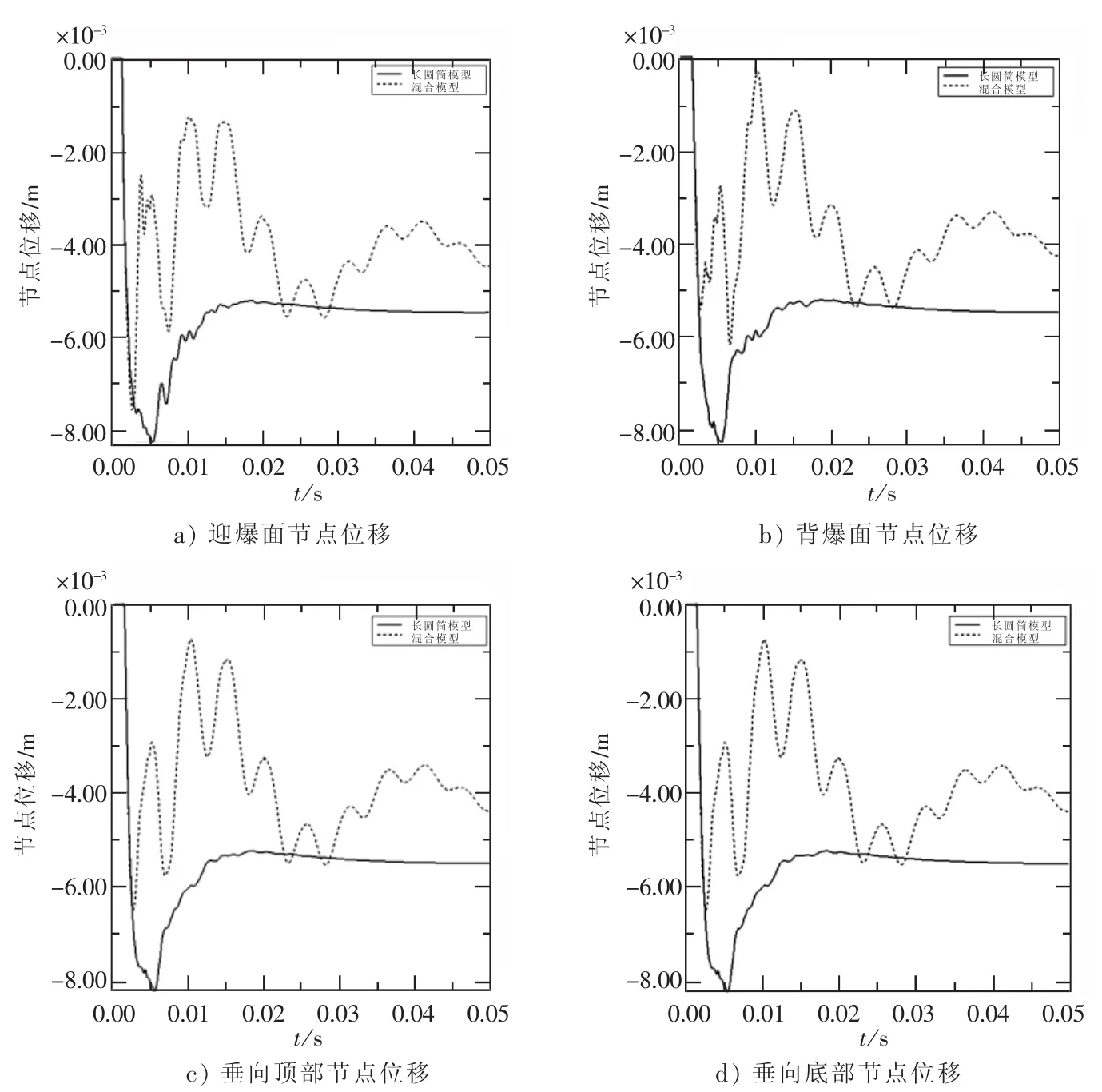
图5 典型节点位移曲线对比
在图4和图5中,虚线表示混合有限元模型的结果曲线,实线表示三维长圆筒模型的结果曲线。从图4中看出,冲击波经过一定的时间传播到结构上,在前2 ms冲击波还未传递到梁单元上时,结果吻合较好。传递到梁单元之后简化模型有较宽幅的振荡,使得结果产生较大的偏差。从图5的位移曲线能清晰地看出这种现象。
导致两者结果产生较大偏差的原因有:
1)将部分圆筒简化为梁单元,虽然其刚度质量等剖面属性相等,梁单元与三维壳单元相比,梁单元只能施加入射压力,而壳单元与流体介质之间耦合产生的散射压力无法计算,因此忽略了壳体振动对入射压力的缓冲作用,使得结构速度{x˙}增大。由式(4)解得的散射波流体质点速度{us}增大,由此导致式(3)中散射压力的增大;所以结构的运动方程中的载荷矢量增大,导致响应增大;
2)应力波在结构中的传播与结构的形状、弹性模量、密度等有关,将部分圆筒简化为梁单元以后,与应力波相关的这些参数发生很大变化,所以应力波的变化是导致结果规律不一致的另一可能原因。
从表1中看出谱速度的结果规律完全不一致,并有较大误差。
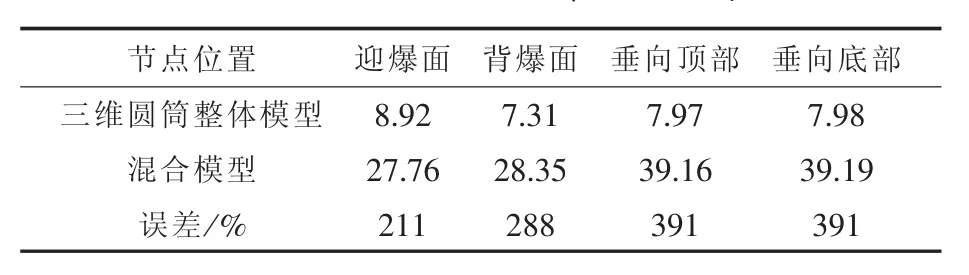
表1 方案1的谱速度(单位:m/s)
4.2 方案2结果分析
下面将三维长圆筒整体模型与1/3圆筒局部模型进行比较分析。选取圆筒中心截面处4个典型节点加速度、位移曲线进行对比。如图6、图7所示。并对典型节点的冲击谱速度进行对比分析(表2)。
在图6和图7中,虚线表示1/3圆筒局部模型的结果曲线,实线表示三维长圆筒模型的结果曲线。从图6中看出,冲击波经过一定的时间传播到结构上,在整个时间段上结果吻合较好,偏差较小,没有宽幅的振荡。从图7的位移曲线能清晰看出局部圆筒模型与长圆筒模型的位移变化规律一致性较好。由于位移曲线反映的是圆柱筒整体位移,局部模型受到的总载荷比长圆筒模型小,所以其整体位移较后者小。从迎爆面和背爆面曲线看出,位移曲线不完全相同,说明存在局部位移,但由于圆筒刚度较大,局部位移较小。由于在冲击环境的考核中主要以加速度为考核对象,所以位移的影响可以忽略。

图6 典型节点加速度曲线对比

图7 典型节点位移曲线对比
导致两者结果产生偏差的原因如下:
1)从结构运动方程式(1)中看出,简化的局部圆筒模型和长圆筒整体模型相比,结构质量矩阵和刚度矩阵不同;
2)从外力公式(2)中可以看出,湿表面积减小,接受入射波压力的面积减小,产生的散射压力也不同,由此导致结构运动方程中的载荷矢量发生变化。由于冲击波属于高频脉冲,冲击波本身衰减较快,且在迎爆面产生较大变形消耗大部分能量,因此认为其局部影响较大。所以简化后的模型对结果的影响有限。
从表2中看出典型节点处的谱速度值规律完全一致,并且误差在工程允许的范围内。误差的大小与节点所处位置的壳体运动有关,在迎爆面所受到的载荷最大,所以其误差也最大。
下面从设计冲击谱的角度,再次证实方案2的准确性(图8、图9)。取误差最大的迎爆面处节点的设计冲击谱进行比较,得出谱位移误差为8%,谱加速度误差为11.5%。
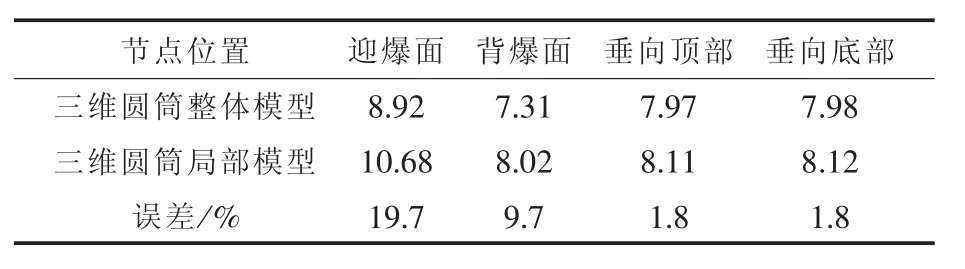
表2 方案2的谱速度(单位:m/s)

图8 三维圆筒整体模型迎爆面节点冲击谱
4.3 不同爆距的结果分析
为了充分验证上述结论,采用与上文中相同的模型、相同的药量,分别对爆距为10 m和26.2 m的工况对3个模型进行了计算,得出的结论与上述一致。由于篇幅的原因这里不再详细列出加速度、位移曲线结果,仅列出谱速度的对比结果。
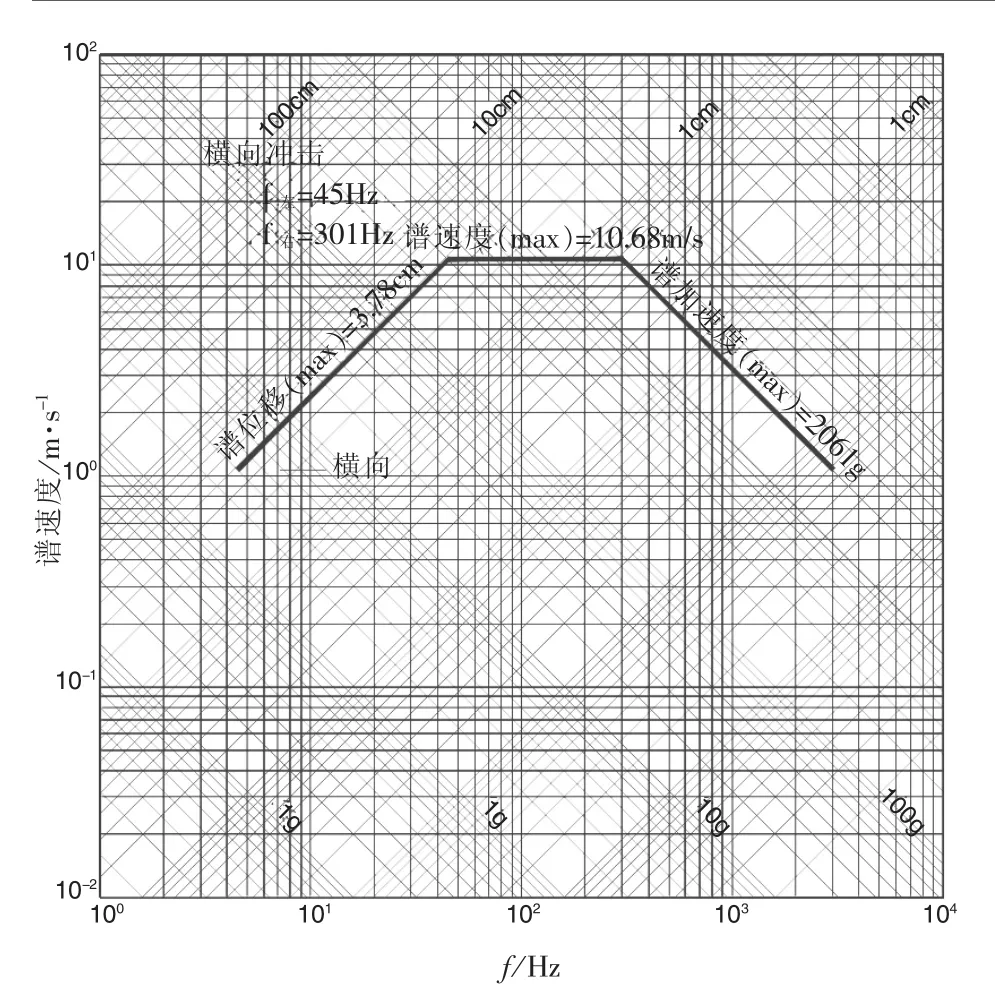
图9 局部圆筒迎爆面节点冲击谱
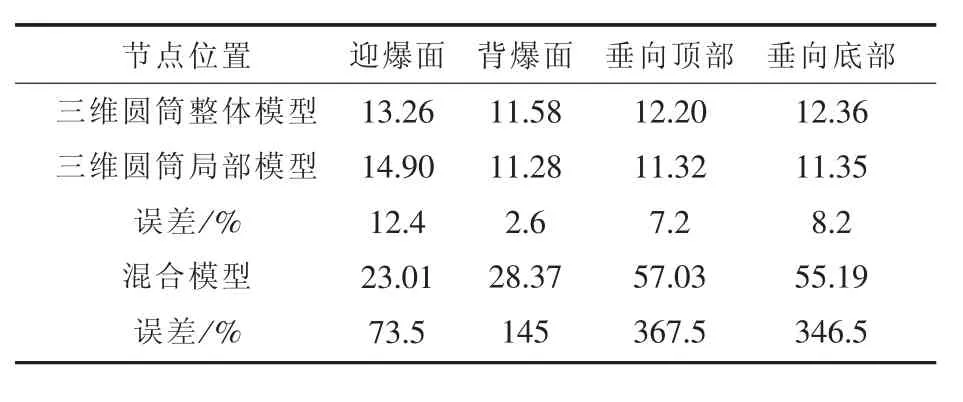
表3 爆距为10 m时,谱速度对比结果(单位:m/s)
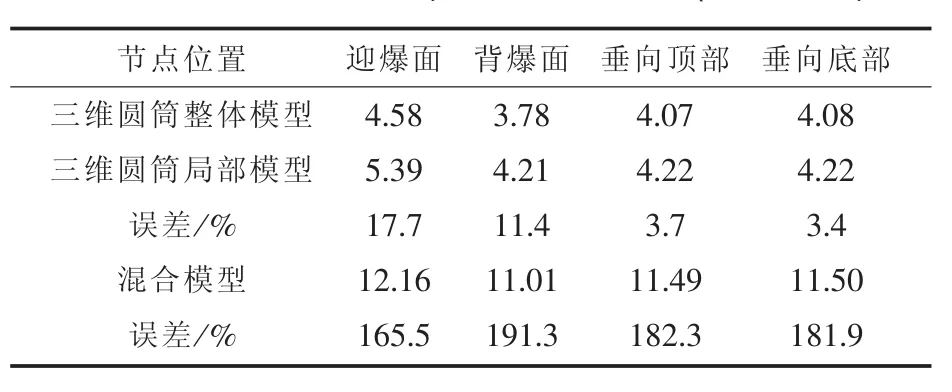
表4 爆距为26.2 m时,谱速度对比结果(单位:m/s)
5 结语
从以上结果可以得出结论,考虑流固耦合作用下,大型水下圆柱壳结构遭受水下爆炸冲击时,简化的局部模型引起的质量和刚度的差别,对计算结果的影响在工程允许的范围内,为了提高计算效率,建立部分结构模型进行冲击响应计算是可行的。使用特殊梁剖面简化的混合模型由于应力波和载荷加载的影响,无法正确模拟,有待于进一步研究。
[1]夏利娟,吴卫国,翁长俭,等.混合有限元模型的集成方法[J].上海交通大学学报,2001,35(4):544-547.
[2]吴梵,郭日修.舰船尾部振动分析整船混合有限元模型的集成方法研究[J].海军工程学院学报,1999(4):.
[3]汪俊.加筋圆柱壳在水下爆炸和静水压力联合作用下的动响应研究[D].CSSRC.2005.
[4]ABAQUS 6.8 Documentation[C],2006.
[5]STILLMAN D W,HALLQUIST J O.LS-DYNA3D User’s Manual[S].LSTC Report,1990.
[6]BELYTSCHKO T.,LIN J.I.,TSAY C S.Explicit algorithms for the nonlinear dynamics of shells[M].Elsevier,1984.
[7]GEERS T L.Boundary element analysis for transient response.In Computational Methods for Transient Analysis[M].Elsevier,New York,1983.
[8]PARK K C.Partitioned transient analysis procedures for coupled field problems:stability analysis[J].Journal of Applied Mechanics,1980,47,(4):370-376.
Method of Simplifying FEM Model of Underwater Cylinder in the Shock Response Analysis
Sun Zhan-zhong Hu Gang-yi Zhang Xin-yu Huang Guo-bing
China Ship Development and Design Center,Wuhan 430064,China
Based on the explicit finite element code ABAQUS,non-linear dynamic response of an immersed cylinder subjected to underwater explosion was analyzed.The response of different simplified models subjected to underwater explosion and the comparisons with the results of the whole model were comprehensively discussed.The results show that satisfactory simulation can be obtained by establishing a part of the model of the cylinder instead of the whole model.
model;simplifying;underwater explosion;impact response
U663.1
:A
:1673-3185(2009)01-22-07
2008-12-20
“十一五”预先研究课题
孙占忠(1983-),男,硕士研究生。研究方向:水下结构冲击响应分析。E-mail:a191221468@163.com胡刚义(1966-),男,研究员,硕士生导师。研究方向:舰船结构动态响应分析
