“企业”号航空母舰阻力预报理论研究

贾敬蓓 宗 智，2 毕俊颖 师华强

1大连理工大学 船舶工程学院，辽宁 大连116024

2工业装备结构分析国家重点实验室，辽宁 大连 116024

“企业”号航空母舰阻力预报理论研究

贾敬蓓1宗 智1，2毕俊颖1师华强1

1大连理工大学 船舶工程学院，辽宁 大连116024

2工业装备结构分析国家重点实验室，辽宁 大连 116024

使用薄船理论，针对美国“企业”号航母进行航母阻力理论预报方法的初步研究。通过文献数据的横向分析比较发现，利用薄船理论计算得到的“企业”号航母的设计速度和该航母公开发表的设计速度吻合良好。该研究可以为航母的阻力预报提供一定的参考。

阻力；薄船理论；Slice方法；预测；美国

1 引言

常规舰艇的阻力预报方法已经基本成熟，对于理论、数值和试验三种方法的精度和适用范围有了比较清楚的认识［1，2］。但是，对于航母公开发表的阻力研究非常少，各种预报方法的精度和适用性的探讨不充分。由于航空母舰是一种以舰载机为主要作战武器的大型水面舰船，需要频繁地进行大量舰载机的起降，所以为了确保在舰载机起降时能够高速迎风航行，增加飞机起飞时对大气的相对速度和降低飞机降落时对舰的相对速度，航空母舰对快速性有更高的要求。因此，航母阻力预报的研究比常规舰艇的阻力预报研究具有更多的内容。作为一个初步的阻力研究，本文偏重于航母阻力预报的理论研究。

在船舶阻力预报的理论研究中，薄船理论是最基本的和最简单的。尽管有诸多的假定，但是作为初步设计时理论指导和阻力优化的便利工具，薄船理论具有计算简单、成本低廉的优势，因此，仍然在广泛地应用。由于航母阻力研究资料公开发表的很少，可参考资料极为有限，所以使用薄船理论，针对美国“企业”号航母进行关于航母阻力理论预报方法初步研究，探究航母阻力的特点，希望为航母阻力预报方法的进一步研究提供可参考的结果。

2 薄船阻力计算

尽管“企业”号航母的体积庞大，但是其长宽比仍然很大，在8左右。因此，从理论上来讲，薄船假定仍然适用。

航行总阻力包括了摩擦阻力和剩余阻力，其中摩擦阻力主要取决于舰船的湿表面积大小。通常近似地把剩余阻力看作兴波阻力来计算，因此，阻力预报工作的关键是确定航母的兴波阻力。

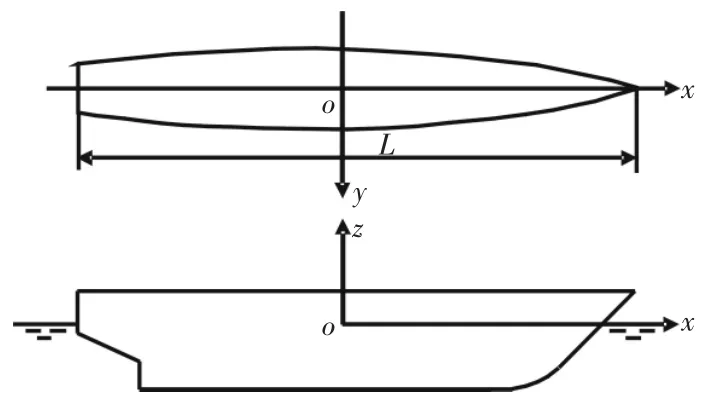
图1 坐标系选取示意图

取如图1中的坐标系，原点在船中位置，ox，oy轴在未被扰动的水面上，ox轴与运动方向一致，oz轴垂直向上。假设船体的长宽比很大，即为“薄船”。设流体无粘无旋，则存在速度势Φ：

式中，U为航速；φ是船体扰动速度势。设船长为L，吃水为T。采用薄船假设，有：

式中，σ是布置在船体中线面上的源强［3］，其数值为：

式中，f（x，z）代表船体水线；G（x，y，z；ξ，η，ζ）是Havelock源速度势（格林函数）。其函数表达式可在［4］中找到。则兴波阻力［5，6］为：

式中，S是船体纵向中心面。

兴波阻力系数为：

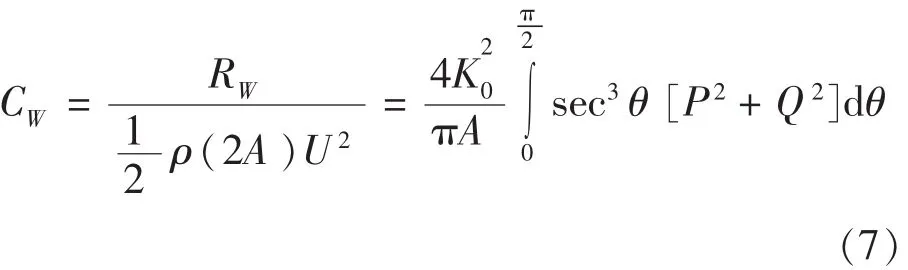
因此，主要的工作集中于计算P，Q。

航母的摩擦阻力系数仍然采用ITTC－75公式来计算，即：

式中，Re是雷诺数，定义为Re＝UL；v是水的运v动粘性系数，取为v=10-6。

3 Slice法

式（5）中的P、Q和船体的型线有关。由于船体的复杂性，直接对式（5）中P、Q进行积分比较麻烦，因此，提出下面的Slice方法进行计算。

切片法在计算船舶运动响应中取得了很好的结果。切片法的特点是忽略沿X轴的纵向流动。主要的计算集中于Y、Z面的横向流动。类似于切片法，在本文中提出Slice法来计算兴波阻力。亦即，将船体沿垂向分成M个薄片，每个薄片的型值为fi（x，z），（i＝1，…，M）。fi（x，z）不依赖于z，亦即fi（x，z）＝fi（x），如图2所示。

图2 切片法和Slice法的比较

于是垂向流动（沿Z轴）就被忽略不计。因此有：

同理，Q为：

由于兴波阻力主要是由纵向流动引起的，故轴方向的流动不能忽略不计。因此，切片理论不适合于船舶兴波阻力的计算。同理，船舶运动受横向流动影响强烈，Slice法同样不适合计算船舶运动，这两种方法集中地体现了船舶运动和船舶兴波的区别。

4 数值处理

上述计算公式中的式（9）、式（10）需进行数值处理，为此考虑如下公式：

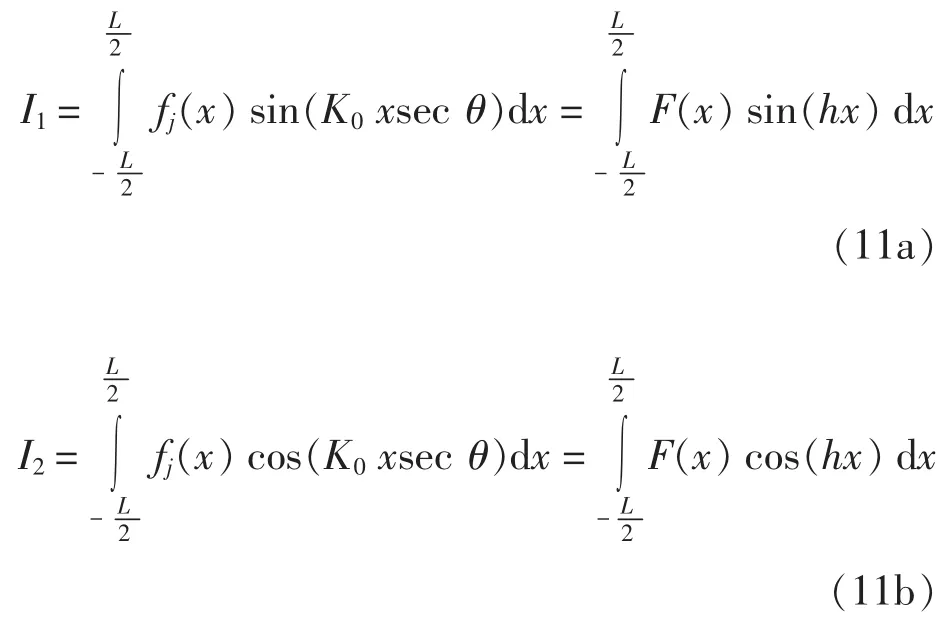
式中，h＝K0secθ。

设F（x）可以由N个立方样条来逼近，亦即，第i段Fi是如图3所示的三阶多项式函数。

图3 立方样条曲线拟合

式中，共有4（N－1）系数ai，bi，ci，di，它们由下列条件确定：

解这些方程，即可获得系数ai，bi，ci，di。于是有：

5 试验验证

将推导所得的兴波阻力计算公式经过数值处理后编制成程序，从而可以计算船体的兴波阻力。

利用已有试验数据来验证本文方法。试验数据取自文献［7］的单体船，其型值由表1给出。计算结果和试验值的比较如图4所示。试验中傅氏数变化范围是从0.3～0.8；计算中傅氏数范围是0.2～0.9。在此范围内二者吻合良好，相对误差小于2.3%。

表1 单体船型值

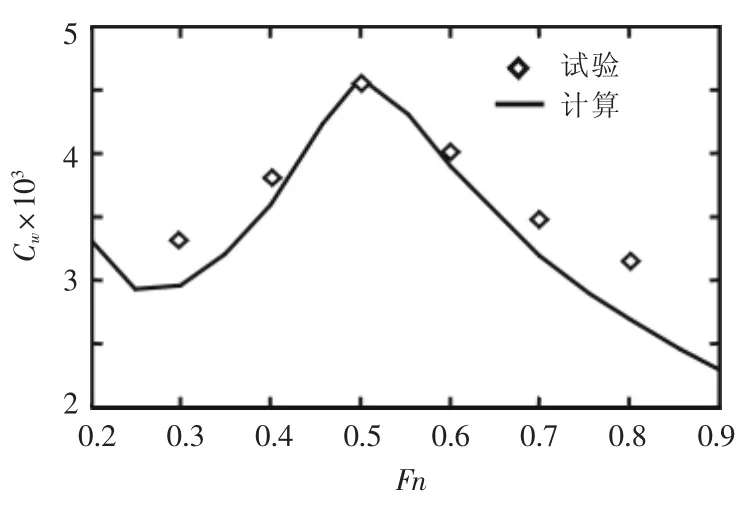
图4 兴波阻力计算和试验比较（试验数据摘自文献[4]）

由此可见，这种兴波阻力的计算方法对于常规船舶来说是适用的，但是这种方法是否同样适用于航母的阻力计算还需要进一步研究探索。因此，尝试使用这种方法对美国“企业”号航母的阻力进行了计算，并且间接地利用航母的已有资料对计算结果进行了评价。

6“企业”号阻力研究

美国“企业”号航母主尺度［8］为：L＝317 m，B＝40.8 m，T＝11.3 m，航母的湿表面积S＝13 162 m2。由于型值的来源受到限制，我们在这里就不给出该舰的型值表。

通过公式（8）对摩擦阻力系数进行计算，其结果在图5中给出。从图中看出，由于航母的湿表面大，摩擦阻力系数变化不大，几乎等于常数。兴波阻力系数Cw使用上面介绍的Slice方法进行计算，其随傅汝德数变化的曲线如图5所示。取粗糙度补偿系数为ΔCf＝0.4×10－3。摩擦阻力系数、兴波阻力系数以及粗糙度补偿系数相加可得到总阻力系数，其变化曲线如图6所示。总阻力由公式即可得到，其曲线如图7所示。

图5 美国“企业”号航母剩余阻力和摩擦阻力系数曲线

图6 美国“企业”号航母总阻力系数曲线

图7 美国“企业”号航母总阻力曲线

对于利用薄船理论计算得到的航母阻力，虽然没有实际的阻力数据进行直接的比较验证，但是从公开发表的“企业”号航母资料中可以间接地检验该计算结果。在文献［8］中，给出了“企业”号轴系收到功率和额定航速，分别为：PD＝209 000 kW，V＝33 kn。一般地，取螺旋桨有效功率为轴系收到功率的60%，即PE＝60%PD，这样就可以得到“企业”号航母的有效功率大致为PE＝125 400 kW。而舰船的有效功率又可以用航行总阻力和航速的乘积来表示，即PE＝RtV。在计算总阻力的基础上，得到的有效功率曲线如图8所示。据此，可以反推出航母在计算阻力状态下的航速为V＝33.8 kn，如图9所示。这与文献［8］给出的航速V＝33 kn非常接近，相对误差小于2.5%，说明计算所得航母阻力与实际阻力比较接近。

另外，文献［9］指出，一艘设计比较成功的航母，其阻力应该处于阻力曲线的平坦段。由图9可以看出，我们计算所得的航母总阻力正好处于阻力曲线的平坦区范围内，这也间接说明了计算所得航母总阻力的合理性。

图8 美国“企业”号航母有效功率曲线

图9 美国“企业”号航母的航速反推结果

7 结语

基于薄船理论和针对美国“企业”号航母，本文尝试研究了航空母舰的阻力预报问题，并针对美国“企业”号航母的阻力进行了计算，最终得到了航母的总阻力计算值随航速变化曲线。通过和文献的数据横向间接地比较，可以看出薄船理论对于像“企业”号这样的航母也是适用的。该方法对于航母的阻力计算也有很好的参考价值。

［1］邵世明，赵连恩，朱念昌.船舶阻力［M］.北京：国防工业出版社，1995.

［2］赵连恩，杜振煌，应业炬.基于兴波阻力理论与阻力图谱资料的高速双体船阻力预报方法 ［J］.船舶力学，2006，10（5）：17－23.

［3］毛政良，石艳青.利用Michell积分计算薄船兴波阻力［J］.武汉水运工程学院学报，1989，13（1）：109－113.

［4］WEHAUSEN J V.The wave resistance of ships［M］.Advances in Applied Mechanics.Academic Press，1973.

［5］蔡新功，孙永华.基于Michell理论的多体船阻力计算［J］.船舶，2007，（2）：5－10.

［6］李世谟.船舶阻力［M］.北京：人民交通出版社，1989.

［7］陈军，卢晓平.用线性兴波阻力理论计算穿浪双体船的兴波阻力［J］.海军工程大学学报，2002，14（3）：53－58.

［8］IRELAND B.Aircraft Carriers of the World［M］.UK：Southwater Publishing，2008.

［9］孙诗南.现代航空母舰 ［M］.上海：上海科学普及出版社，2000.

Theoretical Study of the Resistance Prediction of USS Enterprise Aircraft Carrier

Jia Jing-bei1Zong Zhi1，2Bi Jun-ying1Shi Hua-qiang1
1 School of Naval Architecture，Dalian University of Technology，Dalian 116024，China 2 State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian 116024，China

The study of the resistance prediction method is presented with the thin ship theory for USS Enterprise aircraft carrier.Through the comparison and analysis with published data，it is found that the design speed predicted by the thin ship theory and the actual design speed of the carrier are in good agreement.Thus the methodology presented here provides useful references for the design of aircraft carrier.

resistance；thin ship theory；Slice method；prediction；America

U661.31

：A

：1673－3185（2009）01－13－05

2008－11－21

贾敬蓓（1984－），女，博士研究生。研究方向：船舶与海洋工程流体力学。E-mail：jiajingbei＿1221＠163.com宗 智（1964－），男，教授，博士生导师。研究方向：船舶与海洋工程。E-mail：zongzhi＠dlut.edu.cn