太阳同步轨道卫星的太阳帆板驱动规律研究

翟 坤

（清华大学航天航空学院，北京 100084）

太阳同步轨道卫星的太阳帆板驱动规律研究

翟 坤

（清华大学航天航空学院，北京 100084）

研究一类斜飞斜装特殊的太阳同步轨道卫星。首先确定太阳帆板的开始驱动时刻，并给出地球阴影区的计算方法，然后根据不同情况分析太阳帆板的过程驱动规律，并提出基于 MATLAB/Simulink/RTW软件的数值设计方法，最后以某卫星为例，说明太阳帆板驱动规律的设计过程，并得到满足工程需要的结果，验证该设计方法的准确性和可行性。

太阳同步轨道；帆板；驱动规律；MATLAB；Simulink

1 引 言

卫星在轨道上运行时，所需的能量除本身携带一部分外，主要靠太阳帆板提供。对于面积恒定的太阳帆板，太阳帆板法线和太阳光线的夹角决定了太阳帆板所能提供的能量的多少。郗哓宁等利用球面三角公式推导出太阳光线与载人航天器的太阳帆板法线的最佳夹角公式［1］。太阳同步卫星的轨道平面法线和太阳光线在赤道平面上的投影之间的夹角保持不变，大多数太阳同步轨道卫星只要选择合适的起始时刻来驱动太阳帆板匀速旋转，就能保证太阳帆板法线和太阳光线的夹角保持最佳位置，从而保证太阳帆板输出最多能量［2-3］。

由于现实中的实际需求，卫星斜飞和太阳帆板斜装等特点越来越多地出现在当今太阳同步轨道卫星上。针对这类太阳同步轨道卫星，匀速驱动太阳帆板旋转不能满足最佳光照的要求。

MATLAB/Simulink/RTW一体化设计方法在工程实践中越来越多地被采用。基于MATLAB/Simulink/RTW一体化的设计方法，可以提高效率，缩短设计和研制周期［4-5］。

本文针对卫星斜飞和太阳帆板斜装这类太阳同步轨道卫星，用基于MATLAB/Simulink/RTW一体化的设计方法，进行太阳帆板驱动规律研究。

2 文中所用坐标系及相关术语

（1）卫星本体坐标系Ⅰ：OXbYbZb（简称b系）

原点O在卫星质心；OZb垂直于星箭分离面，指向有效载荷舱，此轴也是卫星的纵轴；OYb在星箭分离面内，垂直指向太阳电池阵，背向数传天线；OXb按右手法则，如图1所示。

（2）卫星本体坐标系Ⅱ：OXaYaZa（简称a系）

将b系绕OXb轴旋转α后形成的坐标系为 a系。原点 O在卫星质心；OZa与卫星纵轴成 α夹角，指向地心；OXa与 OXb轴重合，指向卫星飞行方向；OYa按右手法则。此坐标系为卫星飞行状态坐标系，如图1所示。

（3）轨道坐标系OoXoYoZo（简称 o系）

轨道坐标系OoXoYoZo为参考基准坐标系。原点Oo在轨道上，与卫星质心重合，OoZo指向地心，OoXo指向飞行方向，OoYo按右手法则。

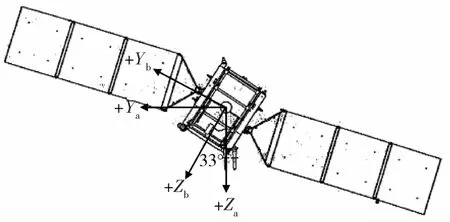
图1 卫星坐标定义

（4）卫星斜飞

卫星以a系为飞行状态坐标系运行，这就是卫星斜飞。

（5）+OYb侧太阳帆板坐标系OspXspYspZsp

原点Osp在+OYb侧太阳阵的连接架与驱动机构（BAPTA，单轴）连接法兰面的几何中心；OspYsp轴沿着太阳阵的轴线，与BAPTA旋转轴重合，与b系的OYb的夹角为β；OspZsp指向与贴片面的外法向一致。OspXsp按右手法则。

（6）-OYb侧太阳帆板坐标系OsnXsnYsnZsn

原点Osn在-OYb侧太阳阵的连接架与驱动机构（BAPTA）连接法兰面的几何中心；OsnYsn、OsnZsn和 OsnXsn与 OspXspYspZsp定义一致。

（7）太阳帆板斜装

太阳帆板斜装是指太阳帆板的轴线与OYb有夹角 β。

3 太阳帆板的开始驱动时刻

设计太阳帆板驱动规律，首先要选择太阳帆板的开始驱动时刻，然后计算地球的阴影区分布，最后设计太阳帆板的过程运动规律。

太阳帆板展开后，处于零位状态，为了便于控制，太阳帆板要等到太阳帆板法线和太阳光线成最小夹角时才开始转动。本节首先根据卫星轨道等已知信息，计算太阳帆板的开始驱动时刻。

太阳同步轨道卫星的轨道半长轴a，轨道偏心率e，轨道倾角i，轨道的升交点赤经 Ω，卫星初始幅角u0（卫星初始位置与地心连线和升交点与地心连线的夹角）均为已知量。

太阳运动轨道的长半轴为as，偏心率为es，轨道倾角为is，轨道的升交点赤经为Ωs，太阳初始幅角为us0。

太阳的赤经αs和赤纬βs可用下式表示或

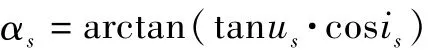
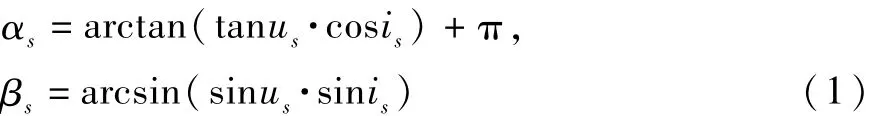
则太阳光线矢量在赤道惯性坐标系中的分量表达式Si为

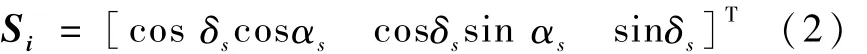
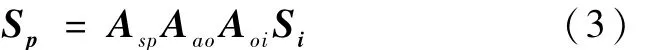
经过三次坐标变化，得到太阳光线矢量在OspXspYspZsp中的表达式 Sp为其中，Aoi是赤道坐标系到卫星轨道坐标系的转换矩阵，Aao是卫星轨道坐标系到 a系的转换矩阵，Asp是a系到OspXspYspZsp的转换矩阵。

而太阳帆板法线矢量在OspXspYspZsp中可表示为

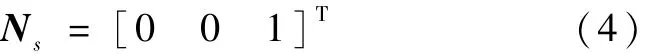
令γ为太阳光线与+OYb侧太阳帆板法线的夹角，则有

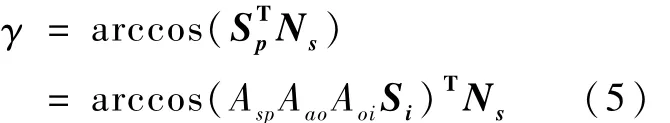
+OYb侧太阳帆板和 -OYb侧太阳帆板平行，它们和太阳光线矢量的夹角是相同的。根据 γ的表达式，代入已知量，应用 MATLAB/Simulink，在一个轨道周期内进行仿真，可找到 γ的最小值，而γ取最小值的时刻就是太阳帆板的开始驱动时刻。

4 阴影区计算

太阳同步轨道卫星运行一个轨道周期，总有一段时间卫星是处于地球阴影区内。而在设计太阳帆板过程驱动规律时，可以通过协调太阳帆板在光照区和阴影区的不同转速，达到太阳帆板和太阳光线的最佳夹角关系。由卫星和太阳的位置关系可以确定卫星进入阴影区的条件，如图2所示。

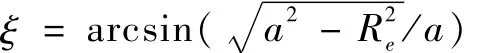
5 太阳帆板的过程驱动规律

太阳帆板开始运动后，在一个轨道周期内，需要驱动太阳帆板合理转动，保证时刻获得最佳光照（即式（5）中的γ时刻保持最小）。针对斜飞斜装的太阳同步轨道卫星，本节分两种情况分析太阳帆板的过程驱动规律。

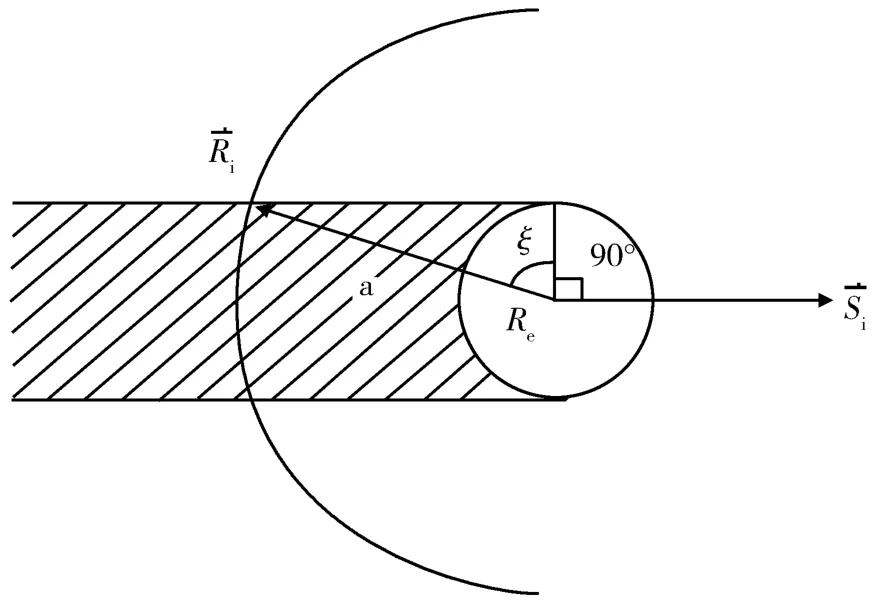
图2 地球阴影区示意图

5.1 太阳帆板驱动轴垂直轨道面

当卫星飞行的倾斜角α和帆板的倾斜安装角β相等时，太阳帆板的驱动轴就垂直于卫星的轨道面。由于太阳同步轨道的固有特点，在这种情况下，当太阳帆板开始运动后，只要使太阳帆板绕驱动轴以卫星轨道角速度匀速转动，即可完全抵消卫星的轨道运动，保证太阳帆板法线和太阳光线始终保持最小夹角不变。

这种情况下，太阳帆板的过程驱动规律比较简单，大部分卫星都是属于这种情况。

5.2 太阳帆板驱动轴不垂直轨道面

当卫星飞行的倾斜角α和帆板的倾斜安装角β不相等时，太阳帆板的驱动轴就不垂直于卫星的轨道面，不能采用匀轨道角速度的过程驱动规律。

根据节 2和节 3的相关论述，在 MATLAB/Simulink下搭建模型，对于一个轨道周期内的任意时刻，都对帆板的转角在0°～360°范围内搜索，找到太阳帆板法线和太阳光线成的最小夹角 γmin，并得出成最小夹角时太阳帆板的转角θ。

MATLAB软件的RTW工具包提供了一种快速仿真目标（简写为 rsim）。rsim可以把太阳帆板光照模型生成快速的单机仿真C代码，从RTW生成的C代码是高度优化的，可加速Simulink模型的仿真速度。同时，快速仿真目标在运行时使生成的代码可从标准MATLAB MAT文件中读取和存取数据。利用这些支持文件，快速仿真目标在仿真过程可从MAT文件中读取新的信号和参数，而不需要重新编译模型。快速的执行速度使其非常适合于蒙特卡罗仿真过程。

通过RTW的快速仿真目标可得到一系列太阳帆板的转角θ，然后通过线性拟合，设计一种可行的太阳帆板过程驱动规律，保证太阳帆板尽量得到最佳光照。

6 仿真分析

下面通过一个实例说明太阳帆板过程驱动规律的设计过程。

假设某太阳同步轨道卫星的轨道要素如下：a=7032.935km，e=0，Ω=58.099°，i=98°，u0=0°。卫星斜飞 30°，即 α=30°，太阳帆板斜装 12°，即 β=12°。

太阳在太阳视运动轨道中的轨道要素如下：as=149597870km，es=0.016707，Ωs=0°，is=23.433°，us0=-92.4°。

（1）计算太阳帆板的开始驱动时刻

把上述已知数据代入式（5），在 MATLAB/Simulink下搭建模型，仿真一个轨道周期5869.7 s。

结果显示，卫星保持太阳帆板零状态运行3301.2s后，达到太阳帆板法线与太阳光线的最小夹角 γmin=11.99°。此时卫星的轨道要素中 Ω=58.137°，u=202.469°，其它不变，太阳轨道要素中太阳的幅角us=-92.36°，其它不变，把这些作为新的卫星和太阳的轨道数据。

（2）计算阴影区

从太阳帆板法线与太阳光线成最小夹角时刻，开始计算一个轨道周期内阴影区的分布情况，即把上述3301.2 s时刻作为计算阴影区的起始时刻，把新的卫星和太阳的轨道数据代入式（6），同样在MATLAB/Simulink下搭建模型，仿真一个轨道周期5869.7s，得到如下仿真结果：

0～1942s时，帆板处于光照区；

1942.1～3927.6s时，帆板处于阴影区；

3927.7～5869.7s时，帆板处于光照区。

（3）计算太阳帆板的过程驱动规律

按照节4.2的叙述，采用新的卫星和太阳的轨道数据，在 MATLAB/Simulink下搭建模型，在 RTW中选择快速仿真目标 rsim，编写仿真所需的 m文件。考虑阴影区的影响，仿真一个轨道周期5869.7s，得到一个轨道周期内的任意时刻太阳帆板法线和太阳光线成的最小夹角 γmin，并得出成最小夹角时太阳帆板的转角θ，如图3和图4所示。

由图3和图4可以看出，在一个轨道周期内的两个光照段，太阳帆板最佳光照对应的太阳帆板的转角曲线不是直线，即太阳帆板的转动是变速的。从太阳帆板的控制等角度考虑，太阳帆板变速转动不可取，对图3和图4中的两条曲线采用线性拟合，得到如下结果：

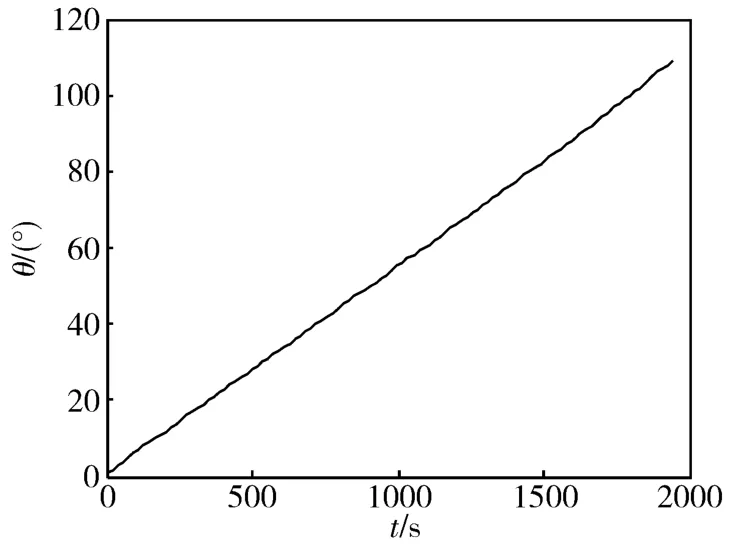
图3 0s～1942s时间段内θ的变化情况

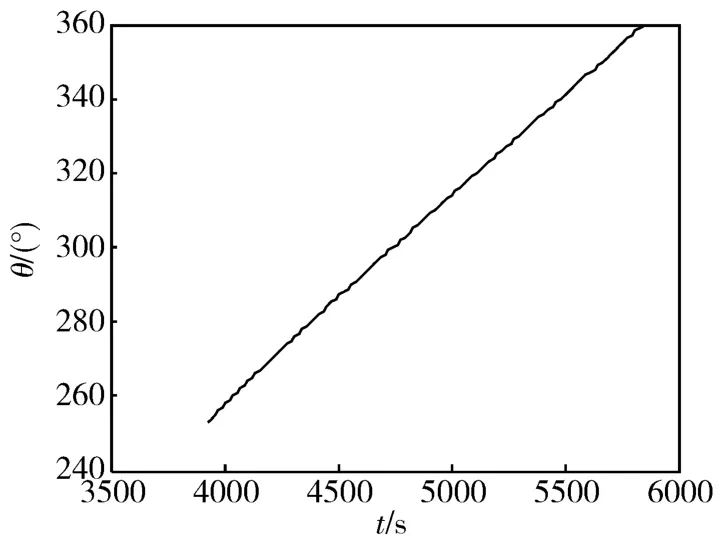
图4 3927.7s～5869.7s时段内θ的变化情况

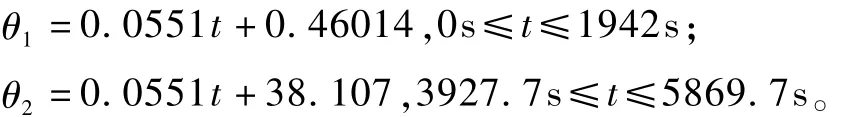
通过协调光照区和阴影区太阳帆板的不同转速，达到太阳帆板的最佳光照，得到如下太阳帆板的过程驱动规律：

1）0s≤t≤1942s，太阳帆板的过程驱动规律为 θ=0.0551t，θ的单位是（°）。

2）1942s＜t＜3927.7s，太阳帆板的过程驱动规律为 θ=0.0735t-35.737。

3）3927.7s≤t≤5869.7s，太阳帆板的过程驱动规律为θ=0.0551t+36.5837。

令γy太阳帆板法线与太阳光在垂直于太阳帆板驱动轴的平面上的投影夹角，工程上常用γy的大小来衡量太阳帆板光照的好坏。根据工程经验，当γy不大于5°时，太阳帆板就能确保整星的能源要求，由式（5）得

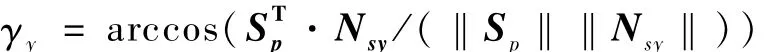
其中‖‖为取模运算，而Nsy为

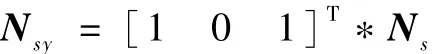
其中*为元素乘。

根据上述设计太阳帆板的过程驱动规律，仿真一个轨道周期 5869.7s，得到如图 5所示的仿真结果。

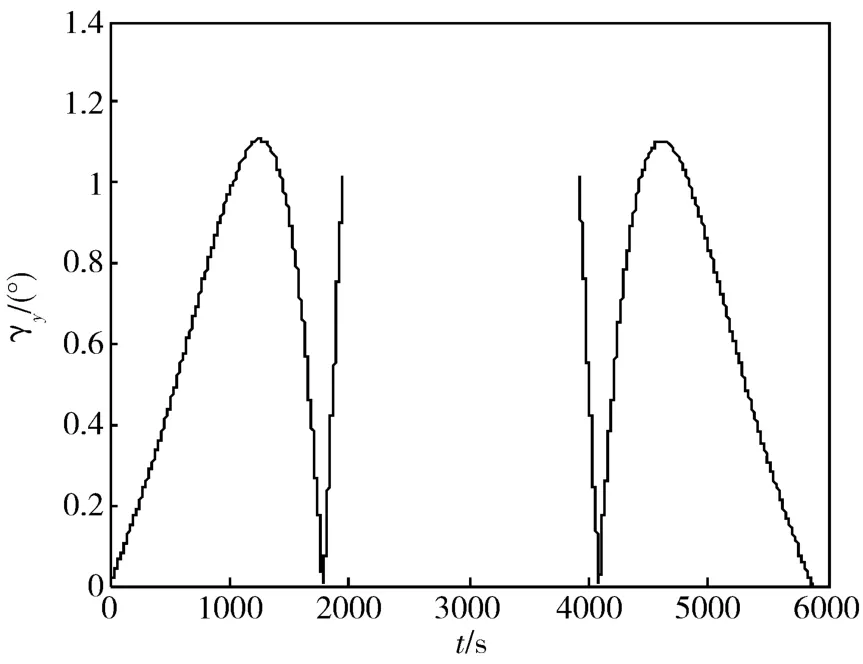
图5 一个轨道周期内γy的变化情况

由图5可知，按照上述设计的过程驱动规律驱动太阳帆板，在一个轨道周期内，γy不大于1.4°，满足工程要求。

7 结 论

本文针对斜飞斜装的太阳同步轨道卫星的太阳帆板驱动问题，进行了详细的分析，并结合MATLAB/Simulink/RTW一体化设计方法，给出了切实可行的计算方法。

太阳帆板驱动轴不垂直轨道面情况下的太阳帆板的驱动规律设计方法属于创新工作，具有应用价值，可供工程实践参考。

［1］ 郗哓宁，吴瑞林，潘亮.载人航天器的发射窗口及太阳能帆板的最佳受晒［J］.中国空间科学技术，1997，（5）：54-60

［2］ 章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998

［3］ Jones H M，Roger N.Design and development of a constant-speed solar array drive［C］.NASA Conference Publication 19thAerospace Mechanisms Symposium，CA，USA，1985

［4］ 杨涤，李立涛，杨旭.系统实时仿真开发环境与应用［M］.北京：清华大学出版社，2002

［5］ The MathWorks Inc.MATLAB real-time workshop user's guide［M］.The MathWorks Inc.，2001

Driving Laws of Sun Synchronous
Orbit Satellite's Solar Arrays

ZHAI Kun
（School of Astronautics and Aerospace，
Tsinghua University，Beijing 100084，China）

A special sun synchronous orbit satellite which flies slantingly and has a pair of slanting solar arrays is investigated in this paper.First of all，the driving time of solar arrays is determined and an algorithm for calculating the earth's shadow area is derived.Then，the process driving laws of solar arrays are analyzed for different conditions and a numerical design method is obtained through the saftware MATLAB/Simulink/RTW.Finally，the design process of solar array driving laws is shown by taking some satellite as an example.Simulation results demonstrate the effectiveness of the proposed method.

sun synchronous orbit； solar array；driving law；MATLAB；Simulink

V423.4

A

1674-1579（2008）04-0038-04

2008-02-19

翟坤（1979-），男，辽宁人，博士后，研究方向为微小卫星姿态控制系统设计（e-mail：zhaikun@mail.tsinghua.edu.cn）。