行波型超声波电机的一种非线性控制模型

徐勤超，张激扬

（北京控制工程研究所，北京100190）

行波型超声波电机的一种非线性控制模型

徐勤超，张激扬

（北京控制工程研究所，北京100190）

研究了行波型超声波电机的结构和工作原理。针对超声波电机的特殊工作原理和强非线性，利用实验测定的方法建立了超声波电机及其负载的频率-转速非线性控制模型。实验结果证明了控制模型的有效性，为超声波电机高性能控制算法的设计和仿真提供了基础。

超声波电机；控制模型；非线性

1 引 言

超声波电机（USM）是一种具有新型工作原理的电机，与传统电磁电机相比具有低速力矩大、动态响应快、可直接驱动、无铁心和线圈、低速平稳无脉动、停电自锁、较适合特殊空间环境等优点。超声波电机可作为空间机械系统和控制系统的驱动装置，符合人造卫星、宇宙飞船、着陆器、航天飞机等飞行器质量轻、体积小、功耗少、噪声低、电磁干扰少的趋势要求，在航空航天领域有较大的应用空间。美国和日本已将超声波电机成功应用到航天领域，取得了比较好的效果［1］。但是超声波电机因其特殊的工作机理，在能量转化和运动形式传递的过程中包含压电陶瓷片振动、摩擦等非线性因素和不确定因素，这些因素相互耦合影响，至今没有能精确描述超声波电机动静态特性的模型，致使超声波电机高性能控制算法的设计和仿真较困难，其优势无法充分发挥。超声波电机涉及到材料学、压电学、摩擦学、控制学等多学科的知识。因此，超声波电机数学模型的研究仍是超声波电机控制领域的一个难点。

国内外许多学者采用多种方法建立超声波电机的数学模型。其中解析建模、等效电路建模和有限元建模等以超声波电机工作原理为依据建立的模型比较适用于超声波电机及其控制器的设计和优化［2-12］。利用实验方法辨识建立的超声波电机的数学模型形式简单，可以准确地描述超声波电机的传递函数特性，比较适用于超声波电机控制算法的设计和仿真［13-16］。文献［13］利用实验辨识的方法建立了行波型超声波电机及其驱动装置的电压-转速一阶标称线性模型，用区间限制和加摄动的方法描述电机参数变化。文献［14］以上述模型为基础设计了鲁棒跟踪控制。文献［15］将描述超声波电机特性的系数拟合为输出速度的函数，建立一阶非线性模型，并设计了鲁棒跟踪控制。文献［16］用最小二乘法拟合超声波电机最大转速-频率、负载转矩-死区的二次函数关系，在电机稳态工作点附近建立了局部线性化模型。实验结果证明，采用实验辨识方法建立的传递函数模型与实际超声波电机系统特性一致，而且控制效果良好。

通过改变驱动频率控制超声波电机，可以充分利用超声波电机低速力矩大、动态响应快且调速范围大等优点，可保持较高的工作效率。本文针对行波型超声波电机特殊工作机理和复杂结构等，以驱动频率为输入信号，转速为输出信号，采用实验辨识与数据拟合的方法，建立了行波型超声波电机频率-转速的非线性控制模型。控制模型是驱动频率的时变函数，可实时描述超声波电机控制过渡过程中模型的非线性变化和电机的动静态特性，为控制算法的设计和仿真提供了依据。仿真结果与实验结果相符，证明了超声波电机模型的有效性。

2 行波型超声波电机的工作原理

行波型超声波电机没有绕组和磁极，不依靠电磁介质传递能量。对超声波电机施加频率和幅值不变、相位差为90°的正弦波驱动信号后，定子上的压电陶瓷由于逆压电效应产生振动合成一路行波，行波的振幅经过弹性体被放大。弹性体表面的点做椭圆运动，通过摩擦作用驱动电机转子转动［17］。行波型超声波电机工作原理如图1所示。

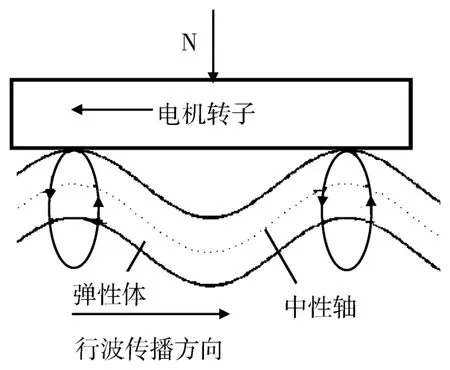
图1 超声波电机的工作原理

3 行波型超声波电机的模型研究

由于超声波电机特殊的工作原理，包括压电陶瓷振动、能量摩擦传递等非线性因素，用机理分析方法对超声波电机建模非常困难。本文以国电南京自动化股份有限公司生产的UMT100型行波型超声波电机作为研究对象，利用已知的等效电路模型设计了驱动电路。然后，根据超声波电机响应特性，建立了超声波电机及其负载的非线性控制模型。超声波电机的测试系统如图2所示。驱动控制电路接收计算机指令，输出两路频率和幅值相同、相位差为90°的PWM信号，经逆变电路升压和匹配电路滤波，输出两路正弦信号驱动超声波电机转动。

3.1 实验设计

本文以超声波电机驱动信号频率（37 kHz～40 kHz）为输入，转速为输出，通过实验确定超声波电机频率-转速关系。对超声波电机施加不同频率的驱动信号获得超声波电机阶跃响应的特性曲线。由电机的阶跃响应特性确定超声波电机的模型形式和模型参数。

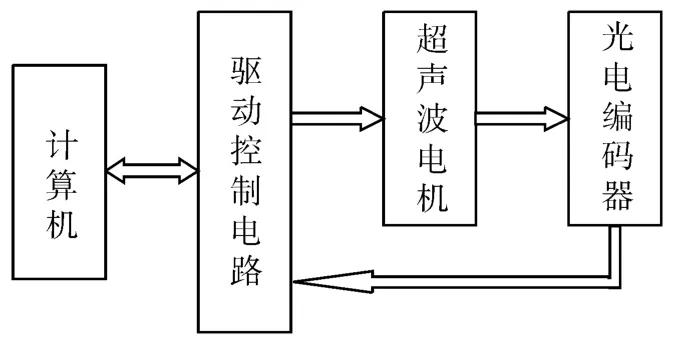
图2 超声波电机的测试电路

3.2 频率-转速特性

行波型超声波电机的驱动频率由定子的谐振频率决定。由于谐振作用，驱动频率与超声波电机的谐振频率差值较小时，定子上压电陶瓷片的振动幅值较大，电机转速较大；而在差值较大时，振幅较小，电机转速较小。因此控制驱动频率与超声波电机谐振频率之差，可迅速控制电机速度。但是由于行波型超声波电机工作过程中包含振动、谐振、摩擦、温漂等因素，导致调频调速具有非线性。驱动频率大于超声波电机谐振频率时，电机转速随驱动信号频率变化缓慢，适合作为工作点。所以本文选择驱动频率大于电机谐振频率的范围作为研究对象。

对超声波电机施加不同频率的驱动信号后，测得电机的阶跃响应曲线，从而获得采用传递函数描述的超声波电机控制模型的验前结构。本文采用不同幅值的阶跃函数信号作为输入进行了多次测试，获得了超声波电机的频率-转速关系，如图3所示。

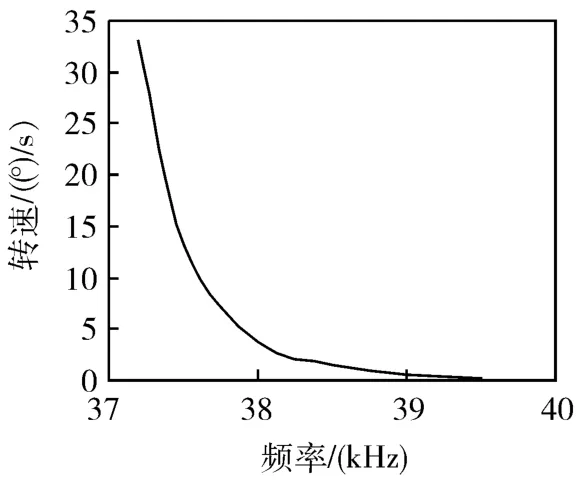
图3 超声波电机转速-频率关系图

3.3 模型分析

行波型超声波电机响应时间很短，一旦加入激励信号，很快就能达到稳定状态，其阶跃响应满足一阶特性［18-19］。由实验结果得出超声波电机的阶跃响应曲线为一阶响应曲线，如图4所示。图中，转速小范围波动是由测速光电编码器测量误差引起的，所以超声波电机的控制模型可用一阶模型表示。设模型的形式为

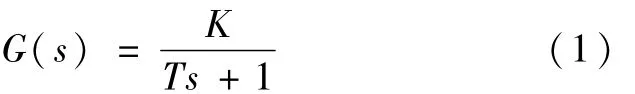
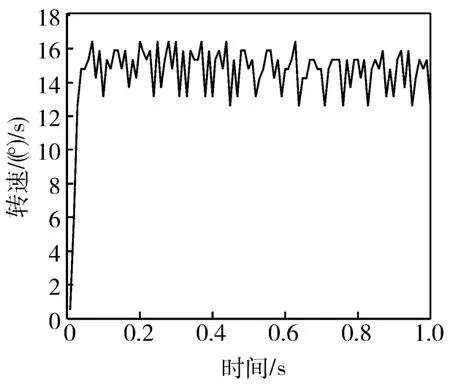
图4 超声波电机阶跃响应曲线

对式（1）所示的系统施加幅值为R的阶跃函数信号，系统的阶跃响应为

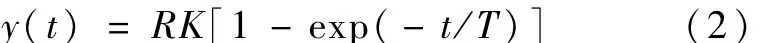
由模型的物理意义知，T表示模型动态过渡时间长短，即动态特性，K表示模型的稳态增益，即输出信号幅值与输入信号幅值的比例关系。当控制对象是线性系统时，由于系统满足可加性和齐次性，K和T为常值。当系统不是线性系统时，K和T将发生变化而不是常值，但如果K和T是与模型本身无关的某种变化规律，则可以确定控制对象的非线性模型。超声波电机的转速与驱动频率呈非线性关系，因此超声波电机的传递函数模型可描述为

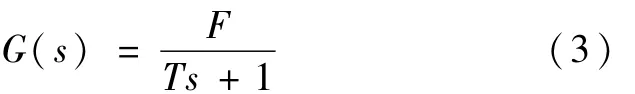
4 超声波电机非线性控制模型的建立

由图3可知，超声波电机转速与驱动信号频率呈指数规律变化，在37 kHz～40 kHz的频率范围内，用最小二乘法拟合二者的关系。根据超声波电机频率-转速特性选择基函数形式为

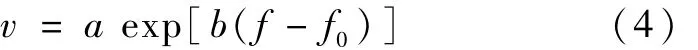
式中，f0为超声波电机的谐振频率；f为驱动信号的频率；v为输出转速；a、b为待定系数。

两边同时取对数

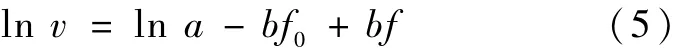
令 u=ln v，c0=ln a-bf0，c1=b，则

由最小二乘曲线拟合［20］与表1的实验结果可得

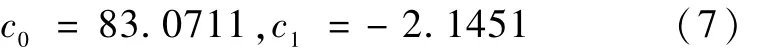
所以，b=c1=-2.1451，取 f0=37，得 a=40.5445，即

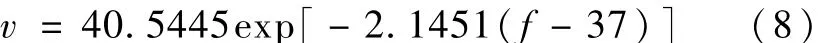
则

F是超声波电机谐振频率和驱动信号频率的函数。不考虑温度漂移引起的超声波谐振频率的变化时，即超声波电机的谐振频率不变时，F是驱动信号频率的一元函数，与模型本身无关。机械时间常数T与电机负载和阻尼有关，当二者保持不变时，T为常值。根据测试结果取均值T=0.005。

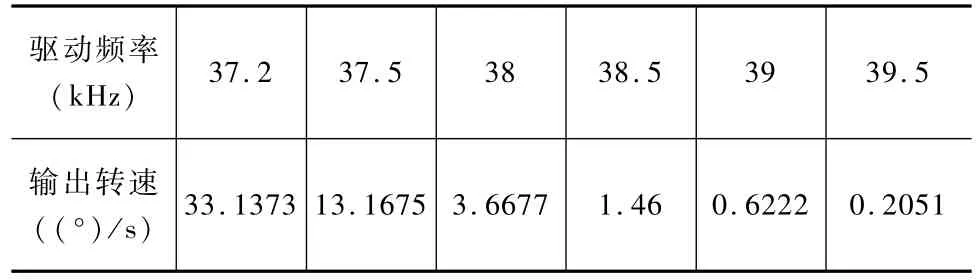
表1 驱动频率与输出转速的关系

5 仿真及实验结果

利用Matlab程序对建立的超声波电机的非线性模型进行了仿真。仿真框图如图5所示。

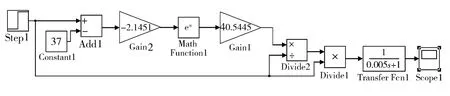
图5 超声波电机模型的Matlab仿真框图

图6显示了对超声波电机控制模型施加不同频率激励信号时的阶跃响应曲线，从仿真结果可知模型显示了超声波电机非线性的稳态增益和极快的动态响应过程。超声波电机闭环控制过渡过程中，电机控制信号逐渐变化，即驱动频率逐渐变化，故超声波电机模型随驱动信号频率而发生改变。一般的控制算法不能满足控制要求。

本文利用非线性控制模型，设计了 PI控制算法，并对超声波电机及其负载进行闭环控制实验。图7显示了依据控制模型设计的PI控制算法跟踪不同幅值阶跃函数信号的仿真结果与实验结果的比较。由实验结果可知，电机工作速度越大，稳态工作点越接近超声波电机谐振频率点，模型对驱动频率的灵敏度越高，模型误差会相应变大；电机工作速度较小时，非线性控制模型与超声波电机传递函数模型的误差很小。

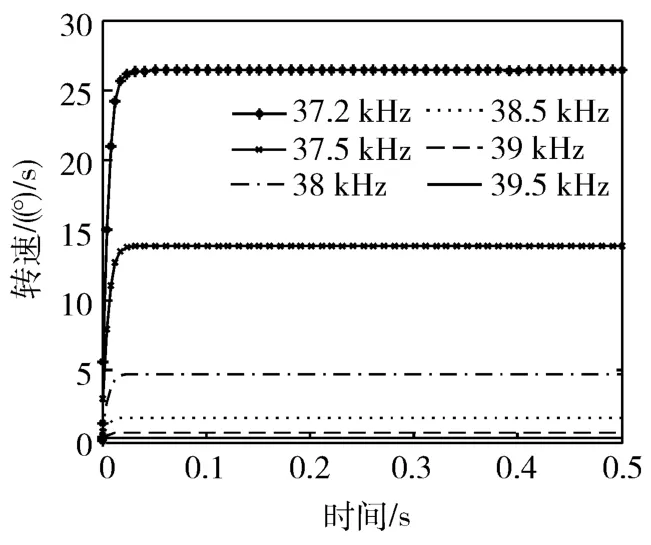
图6 超声波电机转速-频率响应仿真图

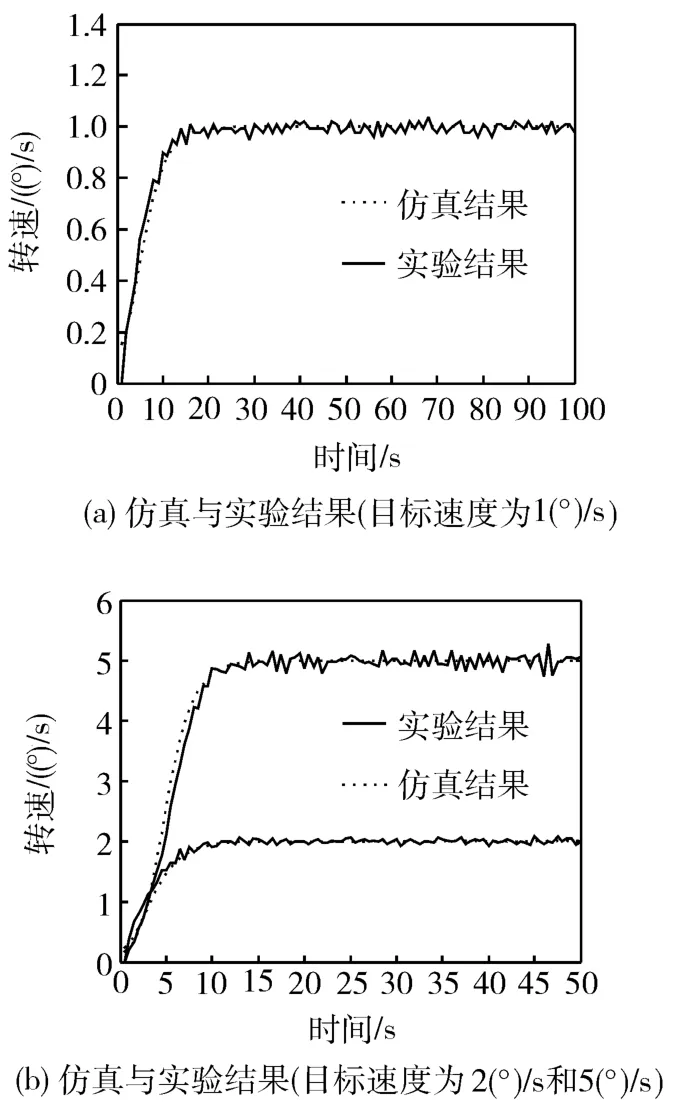
图7 超声波电机PI闭环控制仿真及实验结果

6 结 论

超声波电机与传统电磁电机工作原理不同，其低速力矩大、动态响应快等特点可以弥补电磁电机低速时的不足，但是超声波电机本身包括压电陶瓷片振动、运动摩擦传递等非线性因素，理论建模非常困难。本文利用实验测定和数据拟合的方法，根据电机的输入输出信号关系，建立了超声波电机及其驱动电路、负载的非线性黑箱模型。该模型将超声波电机驱动信号频率与转速的非线性传递函数关系用输入频率描述，反应了电机控制过程中模型的非线性时变规律。仿真和实验结果证明了该模型的有效性，给超声波电机高性能控制算法的设计和仿真提供了基础。

［1］ 陈维山，李霞，谢涛.超声波电机在太空探索中的应用［J］.微电机，2007，40（1）：42-45

［2］ Zharii O Y.An exactmathematicalmodel of a traveling wave ultrasonic motor［C］.IEEE on Ultrasonic Symposium，1994

［3］ Hagood N W， Mcfarland A J.Modeling of a piezoelectric rotary ultrasonic motor ［J］.IEEE Transactions on Ultrasonics， Ferroelectrics， and Frequency Control，1995，42（2）：210-224

［4］ Schulte T， Frohleke N.Parameter identification of ultrasonic motors ［C］.IEEE/ASME International Conference on Advanced Intelligent Mechatronics，Atlanta，USA，Sep 19-23，1999

［5］ Maas J，Schulte T.High performance speed control for ultrasonic motors［C］.IEEE/ASME International Conference on Advanced Intelligent Mechatronics，Atlanta，USA，Sep 19-23，1999

［6］ 刘锦波，陈永校，胡继宗.超声波电机的数学模型及其实验研究［J］.电工技术学报.1999，14（3）：15-20

［7］ Mass J，Schulte T，Frohleke N.Model-based control for ultrasonic motors ［J］.IEEE Transactions on Mechatronics，2000，5（2）：165-180

［8］ 胡敏强，顾菊平，金龙等.超声电动机模型分析的研究［J］.微电机，2002，35（1）：6-11

［9］ 吴新开，何早红，胡俊达.行波型超声波电动机的模型研究［J］.机械工程学报，2005，41（2）：57-60

［10］ 陈超，曾劲松，赵淳生.行波型超声电动机的动力学模型［J］.机械工程学报，2006，42（12）：76-82

［11］ Giraud F， Lemarie-Semail B， Aragones J， et al.Precise position control of a traveling-wave ultrasonic motor ［J］.IEEE Transactions on Industry Applications，2007，43（4）：934-941

［12］ 尤向阳，史敬灼.超声波电机驱动控制系统建模与仿真［J］.微电机，2007，40（10）：77-81

［13］ 雷伏容、钟宜生、徐文立.行波型超声马达的数学模型［J］.压电与声学，2003，25（4）：328-332

［14］ 雷伏容，钟宜生，徐文立.基于区间系统描述的超声马达鲁棒跟踪控制［J］.中国电机工程学报，2004，24（1）：87-91

［15］ 雷伏容，钟宜生，徐文立.基于非线性系统描述的超声马达鲁棒跟踪控制［J］.压电与声光，2005，27（1）：68-71

［16］ Senjyu T， Nakamura M， Urasaki N， et al.Mathematical model of ultrasonic motors for speed control［C］.IEEE Applied Power Electronics Conference and Exposition，2006

［17］ 胡敏强，金龙.超声波电机原理与设计［M］.北京：科学出版社，2005

［18］ 杨明，赵淳生.旋转行波超声马达启动特性的测量及其负载特性的估计［J］.哈尔滨工业大学学报，1998，30（增刊）：261-263

［19］ 胡敏强，王心坚，金龙等.行波超声波电机瞬态特性的测试及分析［J］.中国电机工程学报，2006，26（23）：120-125

［20］ 颜庆津.数值分析［M］.北京：北京航空航天大学出版社，2005：207-215

A Nonlinear Control Model of Traveling-Wave Ultrasonic Motors

XU Qinchao，ZHANG Jiyang
（Beijing Institute of Control Engineering，Beijing 100190，China）

The structure and operation principle of traveling-wave ultrasonic motors are addressed firstly.Based on the special working principle and high nonlinearity，a nonlinear control frequency-velocity model of traveling-wave ultrasonic motor together with the load is established via experiments.The experimental results demonstrate the validity of the nonlinear control model，which is helpful for the design and simulation of the high performance control algorithm.

ultrasonicmotor；control model；nonlinearity

TM35

A

1674-1579（2008）03-0060-05

2008-02-20

徐勤超（1983-），男，山东人，硕士，研究方向为航天器执行机构的驱动与控制（e-mail：publicservant@163.com）。