基于自适应观测器的非线性系统故障诊断*

王小丽，倪茂林

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190）

基于自适应观测器的非线性系统故障诊断*

王小丽1，2，倪茂林1，2

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术国家级重点实验室，北京 100190）

研究一类非线性系统执行器故障诊断问题。对于故障系统，建立一种自适应观测器，通过在线调整，故障后执行器的未知参数被在线逼近。所提出的自适应调整律能够保证观测器稳定及故障估计误差收敛。最后引入卫星反作用飞轮模型，对单飞轮发生故障的情况进行了仿真，结果表明提出的方法有效、可行。

故障诊断；非线性系统；自适应观测器；反作用飞轮

1 引 言

目前，线性系统的故障诊断研究已经取得了丰硕成果，如滤波器方法、广义似然比方法、极大似然比方法、基于观测器/滤波器方法、系统辨识方法、参数估计方法和等价空间方法等，但是研究对象主要是线性定常系统模型。由于非线性系统的特殊性，至今仍然没有统一有效的解决方法，此问题也同样存在于故障诊断领域。对于特殊的非线性系统，人们提出用非线性未知输入观测器方法进行鲁棒故障诊断［1-2］。文献［3］针对离散非线性系统设计了自适应观测器，利用最小二乘法给出了故障估计递推算法。文献［4］设计了神经网络、模糊系统和小波网络故障估计器，对非线性故障模式采用在线逼近的方法进行故障诊断，但是所给出的稳定观测器增益阵的存在性条件仍是一个需要进一步研究的问题。文献［5］针对非线性差分代数系统，将故障辨识问题转化为了参数估计问题，提出了一种基于线性矩阵不等式的故障诊断方法，但是该方法不能用于连续非线性系统的故障诊断。

反作用飞轮是卫星长期在轨运行模式中的主要执行部件，实现对星体姿态角偏差和角速率偏差的精确控制。然而卫星在轨飞行中，由于飞轮长期处于运转状态，很容易发生故障。针对飞轮摩擦力矩增大或某种原因导致的飞轮转速持续下降的故障，本文提出一种自适应观测器的诊断方法，对故障进行检测并且估计出飞轮输出力矩的大小。

2 系统描述及自适应观测器设计

2.1 系统描述

考虑非线性系统

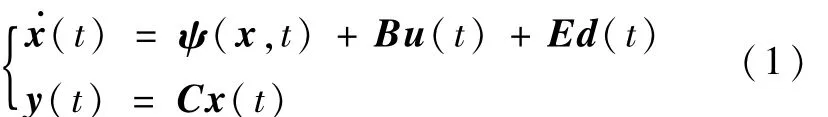
式中，x∈Rn、u∈Rm和 y∈Rp分别是状态向量、输入向量和输出向量。d∈Rq是未知干扰向量，且不失一般性，假设 d为 L2范数有界信号。ψ（x，t）是非线性项，B、C和E均为适当维的常数阵。

假设系统中只存在执行器故障，令 ufi为第i个执行器故障后的实际输出，i=1，2，…，m。故障后系统模型表示为

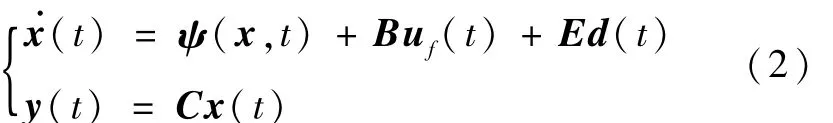
其中 uf=［uf1，…，ufm］T。

2.2 状态观测器设计

针对故障后的系统（2）设计如下状态观测器，对状态向量进行观测

因为发生故障后，执行器的输出值变为未知，所以观测器中的uf用 其估计值代替，可以得到

定义状态估计误差为

那么

将式（2）和式（4）代入到式（6）

将ψ（x，t）在估计值处进行线性化，可以近似得到

作以下假设

2.3 故障的自适应估计

用自适应调整的方法来在线逼近 uf，选取的自适应调整律为

式中，β=diag｛β1，β2，…，βm｝，正数 β1，β2，…，βm为收敛因子，它可以影响自适应估计的收敛速度。P为正定阵，满足以下线性矩阵不等式

其中In×n为n维单位阵，令故障的估计误差为

可以得到下面定理。

定理 1.对系统（2），由观测器（4）和自适应律（8）给出的算法可以保证残差信号）和故障估计误差φ是收敛的。

证明.构造正定二次函数［6］

其中，P为正定阵，满足式（9）所示的线性矩阵不等式，β为式（8）中定义的收敛因子。考虑不包含干扰的系统，由式（7）和式（8）可得

式（11）可以进一步转化为

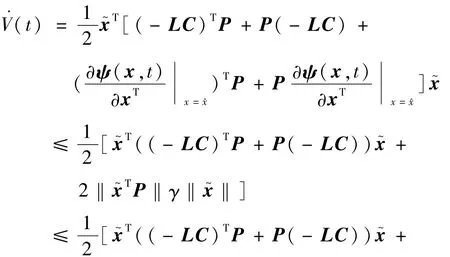
3 三轴稳定卫星执行机构的故障诊断

3.1 卫星姿态动力学模型

考虑由三个正交安装的反作用轮组与星体构成的动量系统，其姿态动力学方程为

其中，I为卫星在本体坐标系中的转动惯量阵，ω=［ωxωyωz］T是卫星惯性角速度在本体坐标系中的分量，h为飞轮角动量，Td为干扰力矩，且

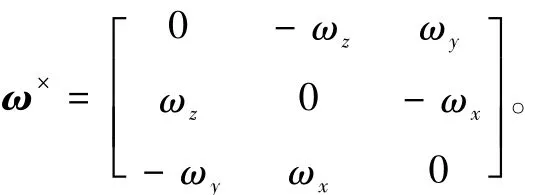
3.2 卫星姿态运动学模型

设姿态四元数为 q=［q0q1q2q3］T=［q1q2q3］T，q为轨道坐标系旋转到星体坐标系的四元数，则卫星姿态运动学方程为

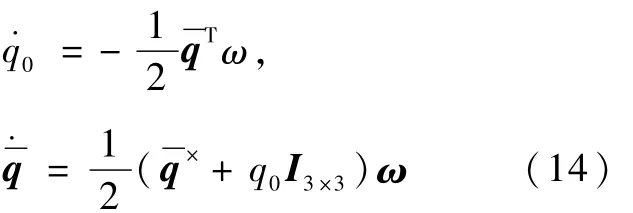
3.3 反作用飞轮数学模型

正常情况下，飞轮的数学模型［7］如下

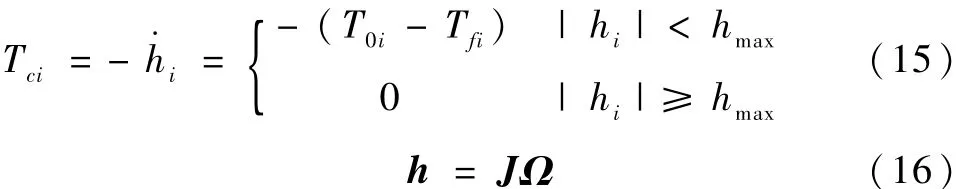
其中输入力矩为

式中，i=x，y，z。Tc=［TcxTcyTcz］T为飞轮输出控制力矩，Tf=［TfxTfyTfz］T为飞轮摩擦力矩，h=［hxhyhz］T为飞轮角动量，J为飞轮惯量阵，Ω=［ΩxΩyΩz］T为飞轮转速，hmax为动量轮最大角动量，Uh=［UhxUhyUhz］T为输入控制指令，即控制器输出，Tmax为最大电磁输出力矩。其中 sgn（·）为符号函数，

考虑飞轮摩擦干扰力矩为

其中干摩擦为 Tf1=［Tf1xTf1yTf1z］T

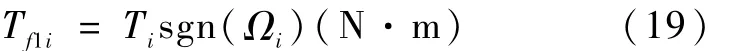
式中，i=x，y，z。力矩 Ti可能是变化的，但通常视为一常值。式（19）所示的近似表达式在飞轮转速不太低的情况下是正确的，当转速较低时，干摩擦特性比较复杂，实际上为一非线性曲线。本文近似采用式（20）［8］来表示

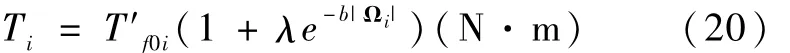
其中

式中，i=x，y，z。Tf0=［Tf0xTf0yTf0z］T为静摩擦力矩，T′f0=［T′f0xT′f0yT′f0z］为动摩擦力矩。

粘性摩擦力矩为

式中，KH为粘性摩擦力矩系数。

3.4 非线性四元数反馈控制律

采用Lyapunov直接方法进行控制器设计基本上有两种方法［11-12］：第一种方法首先假设控制律的一种形式，然后找到一个 Lyapunov函数，来判断所选取的控制律能否导致系统稳定；第二种方法则先构造一个Lyapunov函数，然后找到一个其对应的控制律使得系统全局稳定。以下采用第二种方法。

选取二次函数

其中，选取正定阵Kq，使K-1I也为正定阵。显然，V为正定函数，其导数为

考虑不包含干扰的系统（13），即不考虑干扰力矩Td和摩擦力矩 Tf，把式（13）和式（14）代入式（24）中可以转化为

则式（25）可以转化为

非线性项 ω×H保持在较低的水平，ω×H≈0，可以视为干扰，把式（14）代入到式（26）中可得

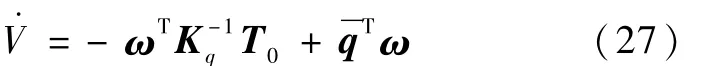
选取控制器输出的控制力矩矢量T0，取为

其中，Kq，Kω为正定阵。μ=-1时输入项抵消陀螺耦合项，μ=0时不抵消。则

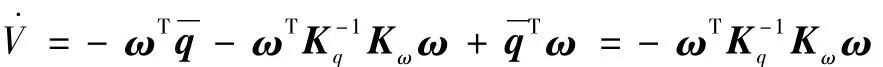
选取适当的 Kq和 Kω，保证Kω为正定阵，则当且仅当 ω=0时，V·=0；∀ω≠0，＜0。根据Lyapunov稳定性定理可知，选取的控制律（28）可以使闭环系统是内部稳定的［6］，平衡点为 ω=0，q=［1 0 0 0］T。

当q0＜0时，选取二次函数为

相应地，控制律取

综合式（28）和式（29），选取控制律为

4 仿真实例

根据式（13）～（16）可得形如式（1）的状态方程，其中，x=［ωTΩT］T，u为执行器正常情况下的输出力矩 Tc，d为干扰力矩Td。

假设卫星的惯量阵为

轨道角速度为ω0=1×10-3rad/s。卫星所受的干扰力矩按以下形式计算［11］

其中α为干扰系数，这里取 α=10-3。三轴飞轮的转动惯量阵设为

假设初始姿态四元数为初始姿态角速度为：ω=0（rad/s），选取控制律为选取观测器增益阵为

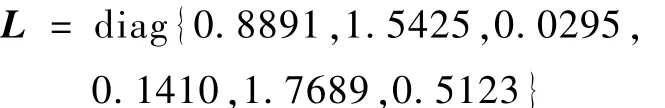
选取 γ=0.01，收敛因子取为 β=10-5I3×3，根据MATLAB中的LMI工具箱求解线性矩阵不等式（9）可以得到正定阵P

飞轮正常工作时，仿真曲线如图1所示。由图1可以看出闭环系统平衡点为ω=0，且给出的算法可以有效估计出飞轮输出力矩大小。

下面考虑飞轮故障情况，假设同一时刻只有一个部件发生故障，分以下几种情况。

（1）飞轮摩擦力矩增大

导致飞轮摩擦力矩增大的主要原因是润滑不当造成损耗力矩增大，严重时会造成轴承损坏，产生重大故障。损耗力矩增大的其他原因还有轴承保持架的不稳定、壳体泄漏导致内部真空环境密封失效、飞轮内压力降低等。

文中仅研究x轴飞轮摩擦力矩突然增大的情况，假设在t=500s时，摩擦力矩增大0.1N·m。仿真曲线如图2和图3所示。

由图2可以看出，在 t=500s时，x轴飞轮输出力矩有一个突变，最后又趋近于稳定，这是因为摩擦力矩增大时，使控制器输出力矩相应地增大，以减小摩擦力矩的影响。由图3可以看出在t=500s时，x轴飞轮输出力矩估计误差显著偏离零点，说明x轴飞轮出现了故障，并且估计误差最终趋近于零，说明给出的算法可以保证估计误差信号的收敛。

（2）飞轮转速持续下降

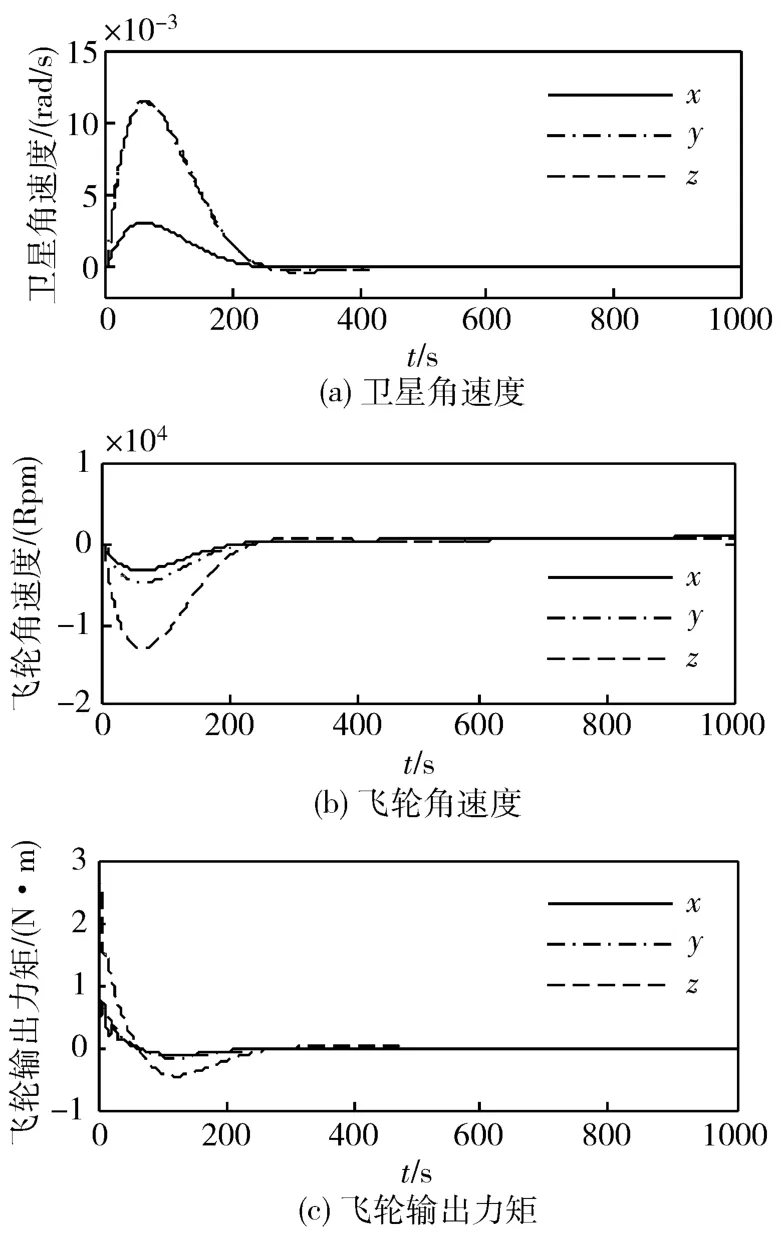
图1 飞轮正常工作时的仿真曲线

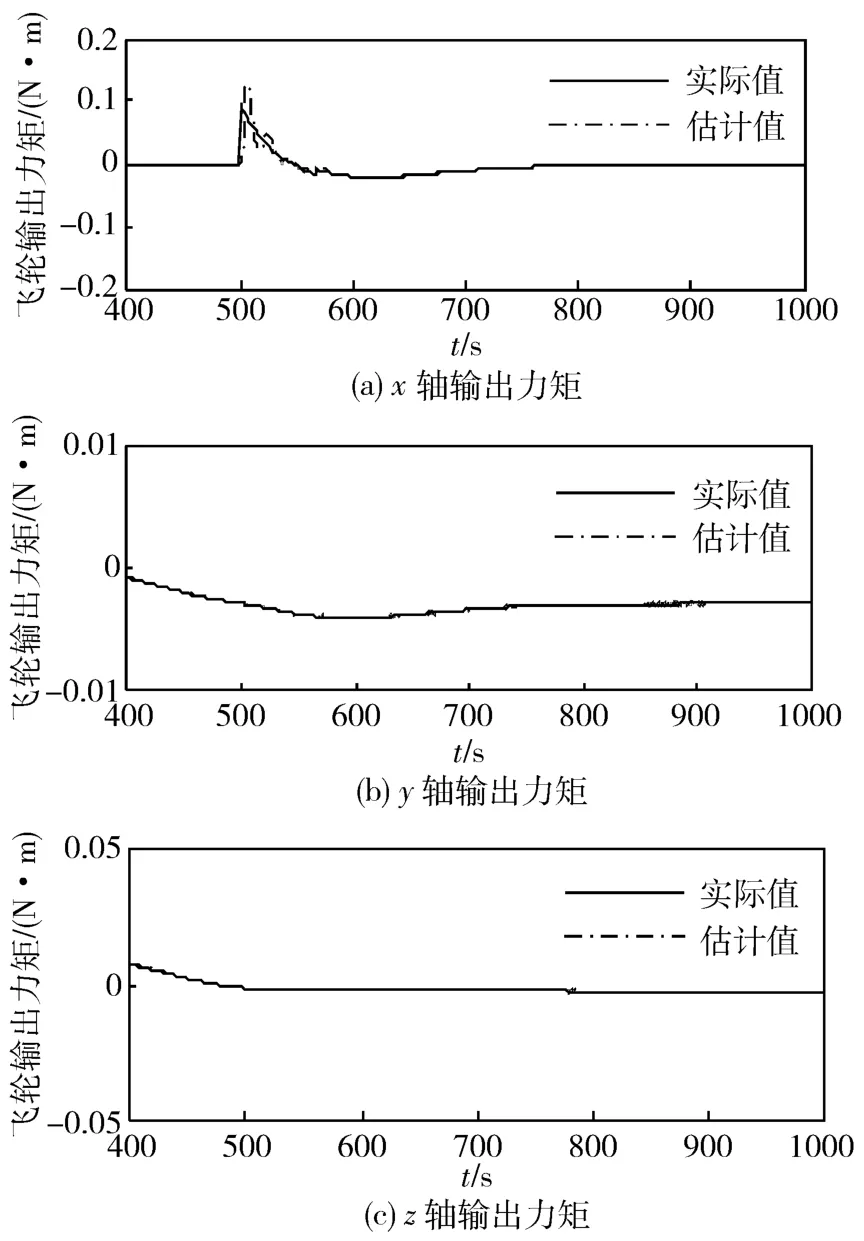
图2 飞轮摩擦力矩增大时的输出力矩

图3 飞轮摩擦力矩增大时的输出力矩估计误差

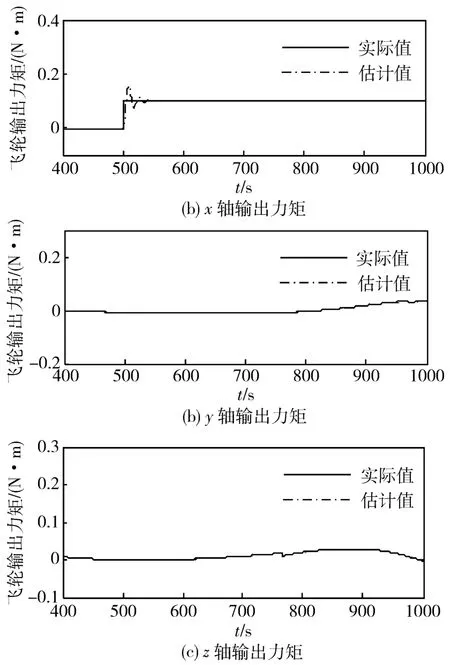
图4 飞轮转速持续下降时的输出力矩

假设由于某种原因使飞轮输出力矩在其转速达到饱和状态前维持在一个常值，那么飞轮转速表现为持续下降的现象。假设x轴飞轮在500 s时发生故障，其输出力矩为常值，y轴和z轴飞轮正常工作。那么在 |hi|＜hmaxi（i=i，y，z）范围内，设仿`真曲线如图4和图5所示，由图4可以看出，x轴飞轮在500s时发生故障，并且输出力矩恒为0.1N·m，y和z轴飞轮正常工作。由图5可以看出，故障估计误差是收敛的，误差最终趋近于零。可见，对于单轴飞轮发生故障的情况，第2节中给出的算法可以诊断出故障，并且可有效地估计出故障的大小。

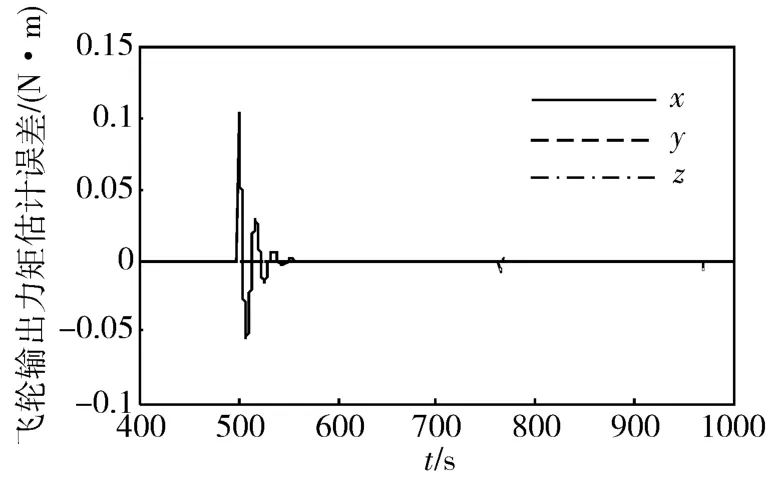
图5 飞轮转速持续下降时的输出力矩估计误差

5 结 论

本文针对连续非线性系统执行器故障的情况，提出了一种自适应观测器诊断方法。该方法能够保证故障估计误差信号的收敛，并且能有效地估计故障。接着对卫星反作用飞轮发生故障的问题进行了研究，针对系统中单轴飞轮故障情况进行了仿真，结果表明本文给出的方法能够有效地检测出飞轮故障。

［1］ 陈茂银，周东华.一类非线性系统的鲁棒故障诊断［J］.山东大学学报（工学版），2005，35（6）：36-39

［2］ 张正道，胡寿松.基于未知输入观测器的不确定非线性系统故障检测［J］.南京航空航天大学学报，2005，37（3）：288-291

［3］ 贾明兴，王福利，毛志忠.基于自适应观测器的一类非线性系统鲁棒故障诊断［J］.自动化学报，2004，30（4）：601-607

［4］ 魏晨，陈宗基.非线性系统的鲁棒故障检测与诊断［J］.自动化学报，2003，29（6）：976-980

［5］ 陈玉东，翁正新，施颂椒.基于 LMI的非线性差分——代数系统的鲁棒故障诊断［J］.自动化学报，2004，30（1）：57-63

［6］ 倪茂林，吴宏鑫，谌颖.鲁棒渐近跟踪控制器设计的新方法［J］.自动化学报，1993，19（2）：213-217

［7］ 邢琰.卫星闭环姿态控制系统的故障检测与隔离［D］.中国空间技术研究院博士学位论文，2003

［8］ 廖晖.对地定向三轴稳定卫星姿态确定和控制系统研究［D］.西北工业大学博士学位论文，2000

［9］ 冯璐，龚诚，何长安.刚体飞行器大角度机动的反馈非线性化控制［J］.飞行力学，1999，17（4）：28-32

［10］ 冯璐，周建国，龚诚，何长安.用于刚体姿态控制的一种非线性反馈控制器［A］.中国控制会议论文集［C］.北京：国防大学出版社，1998.249-253

［11］ 周军.航天器控制原理［M］.西安：西北工业大学出版社，2001

An Adaptive Observer Based Fault Diagnosis for Non linear System s

WANG Xiaoli1，2，NI Maolin1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

The fault diagnosis for nonlinear systems is investigated in this paper.An adaptive observer is designed to estimate on-line the unknown parameters due to faults.By using an adaptively regulating algorithm，the observer is ensured to be stable and the estimation errors are guaranteed to converge.A reaction wheel model of the satellite is employed.Numerical simulations demonstrate that the proposed approach can detect the faults of a single reaction wheel，and estimate the faults effectively.

fault diagnosis；nonlinear system；adaptive observer；reaction wheel

*国家自然科学基金（60774002，90405017）及973课题（2002CB312200）.

2008-02-19

王小丽（1983-），女，山西人，硕士，研究方向为系统故障诊断与容错控制（e-mail：Wangxiaoli502@yahoo.com.cn）。

TP273

A

1674-1579（2008）04-0033-05