近地卫星利用光学敏感器的自主导航方法

杜耀珂，彭仁军（上海航天控制工程研究所，上海200233）

近地卫星利用光学敏感器的自主导航方法

杜耀珂，彭仁军（上海航天控制工程研究所，上海200233）

基于光学敏感器的卫星自主导航技术是利用红外地球敏感器（IRES）和星敏感器（ST）等姿态测量部件提供的测量信息，通过计算含有轨道信息的星光角距和地球视半径角，修正由轨道动力学模型递推得到的轨道参数。通过系统状态模型和观测模型的离散化和线性化，得到扩展卡尔曼滤波算法的递推关系，并在此基础上进行数学仿真。仿真结果表明，该方法的收敛速度和收敛精度都比较好。由于该方法不需要增加额外的星载敏感器，因此具有很好的应用前景。

自主导航；扩展卡尔曼滤波；星敏感器；姿态敏感器

1 引 言

卫星自主导航是指卫星在不依赖地面设施的条件下，利用自身所携带的敏感器获取卫星位置和速度信息的过程。目前，卫星的自主导航主要有天文导航和基于导航卫星的导航两大类。天文导航是利用天体信息来确定卫星位置的导航方法，其优点是具有完全自主性［1-2］。而国际上比较成熟的卫星自主导航系统，如 GPS、GLONASS等系统都被少数国家控制，中国只是被动的使用者，这种局面对中国航天领域的发展，特别是对于提高军事应用卫星的在轨生存能力非常不利。

近年来，中国卫星的光学敏感器技术发展日趋成熟，如IRES、ST等，在卫星中得到了广泛应用，在高精度姿态测量与确定方面，取得了很好的效果，但是在卫星的轨道测量方面，中国则长期依赖于地面遥测和GPS等。

文献［3］给出了利用磁强计和 ST进行自主导航的方法，但是这种方法存在精度不高和计算量较大等不足。本文在某型号卫星配置ST和IRES的基础上，提出了将ST测量得到的恒星矢量和IRES测量得到的地心矢量作为观测量，进行卫星自主定轨的方法。该方法不需增加现有星上敏感器的数量，利用已经成熟的姿态测量技术，经过滤波计算，在卫星姿态比较稳定的情况下，可以实现较高精度的卫星自主轨道确定。

2 卫星的轨道动力学模型

2.1 卫星轨道运动的状态方程

卫星在空间运动时，除了受到地球引力的作用外，还受到月球、太阳和其他天体引力、太阳光辐射压力等其他摄动力的作用。但这些摄动力与地球引力相比都比较小，大约在 10-3量级以下［4］。此外，对于中低轨道的卫星，大气阻力的影响较大，因此，这也是卫星导航计算中必须考虑的因素。为了简化分析问题，这里认为卫星受到的主要力是地球引力。在仿真建模中除地球引力外，可假设其他各种力为系统的干扰力。在此假设条件下，卫星的轨道运动的状态方程可简化为［5］

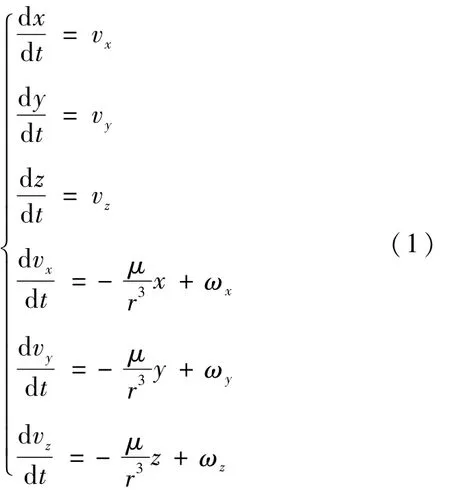
其中，μ为地球引力常数；x，y，z为卫星的三轴位置；vx，vy，vz为卫星的三轴速度；ωx，ωy，ωz为三轴的动态噪声。

针对本文的需要，将卫星的三轴位置与速度信息作为6个状态变量，即将状态变量取为X=［x，y，z，vx，vy，vz］T，则式（1）可表示为

为了提高一步预测的精度，考虑 J2（地球扁率对卫星的二阶摄动影响）项造成的影响，干扰力的量级为 10-3，方差为 10-5～10-4量级［4］，将式（1）的后三个式子展开，得到

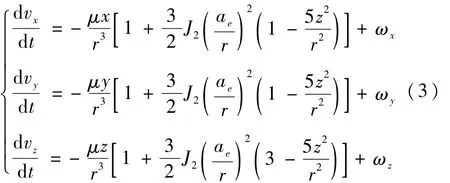
其中ae为地球的赤道半径。

在滤波计算的一步递推中，由于计算量不大，可以按照式（3）［4］进行计算，从而提高一步递推计算的精度。

2.2 自主导航的观测模型

利用IRES和 ST的输出信息，通过计算、比较地球视半径角ρe（图1所示）与星光角距 α（图2所示）来修正卫星的轨道参数。

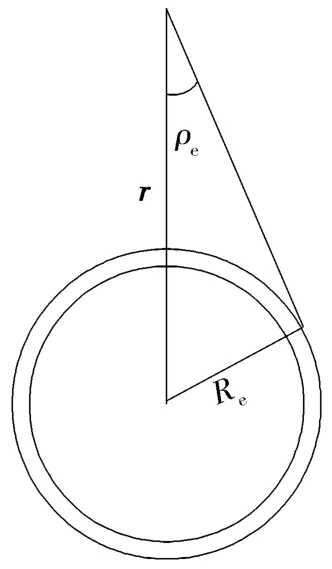
图1 地球视半径角ρe

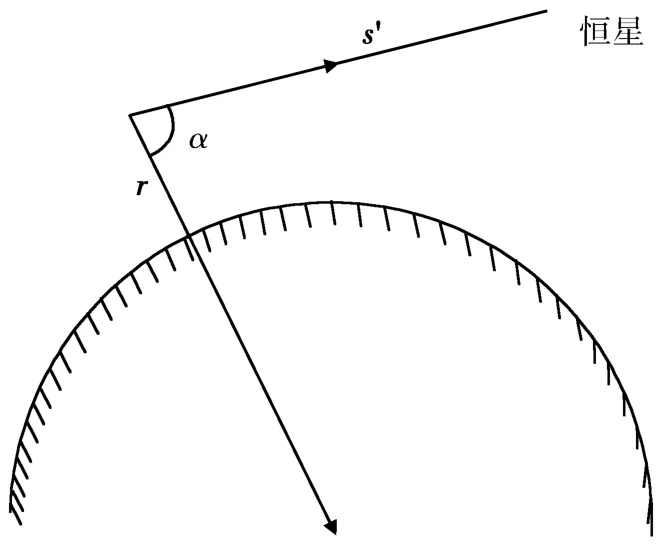
图2 星光角距模型

图1中r为卫星到地心的矢量；ρe为地球的视半径角；Re有两个部分：一部分是地球的平均半径另一部分是地球大气层中能够吸收可见光中波长为15μm光线的二氧化碳吸收带的平均高度，取典型值RIR=40 km，所以Re=+RIR。ρe与 Re和 r之间的关系为

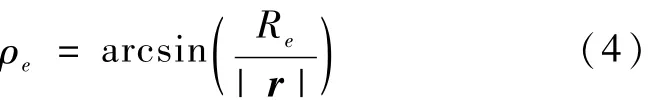
由于IRES为双轨迹的敏感器，因此当IRES在4/4模式（卫星长期在轨运行过程中，姿态稳定时的工作模式）下工作时，在一个扫描周期内，由两个对称的扫描轨迹可获得4个红外穿越角（见图3），这4个穿越角依次为 φ1、φ2、φ3和 φ4，它们分别对应于穿越地球边界的4个时刻。IRES根据光轴的转动速度就可以计算出4个角度值。由以上4个穿越角可以计算并得到

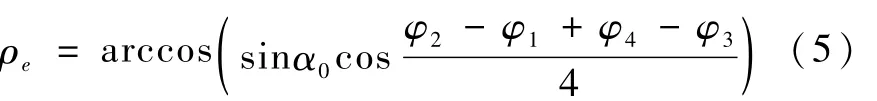
其中α0为红外的扫描锥角。式（5）是根据IRES的使用说明得到的，具体的推导过程较多，此处从略。由以上4个穿越角还可以计算并得到卫星的滚动角φ和俯仰角θ，从而得到在卫星本体坐标系下地心方向矢量

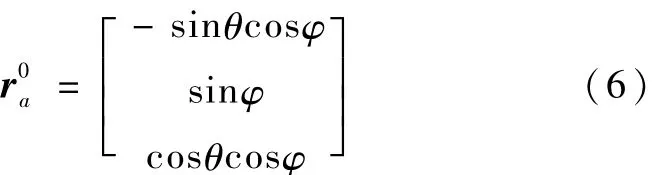
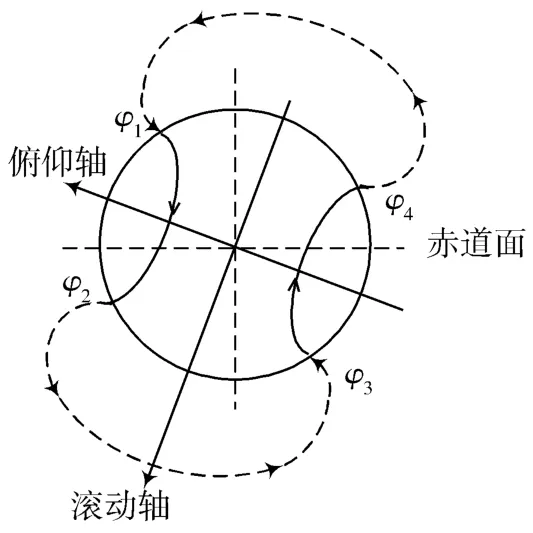
图3 红外穿越角

根据ST提供的信息，可以从中选取3～5颗恒星（超过3颗即可，星数越多越能提高测量的精度，但数量过多会导致系统的计算量过大），根据选取的星体的位置矢量，再结合上面给出的地心矢量信息，就可以计算并得到卫星的星光角距α。

s′表示根据 ST的测量信息计算得到的恒星矢量，在星体坐标系下此矢量用sa进行表示，则有

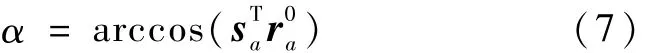
在 EKF算法［6］中，观测模型为

其中，z为实际测量得到的角度，z=（α1，α2，α3，ρe）T，α1、α2、α3表示三个星光角距值；v为观测噪声矢量）为利用轨道递推得到的轨道参数X，经计算后得到的角度信息。比较实测计算值和轨道递推计算值，可以修正轨道递推得到的位置和速度信息。

2.3 EKF的应用

通过对系统动力学方程（2）的离散化和线性化可以得到

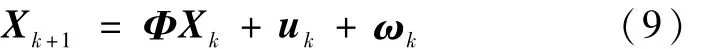
实际应用EKF算法时，由于计算量不大，在进行状态量的一步递推时，可以采用非线性模型，因此uk的具体形式并不需要知道。

观测模型的线性化结果为

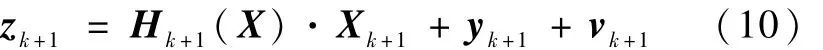
其中，yk+1=［h（Xk+1/k，k+1）-Hk+1（X）Xk+1/k］，是h（X）的线性化矩阵，具体形式为

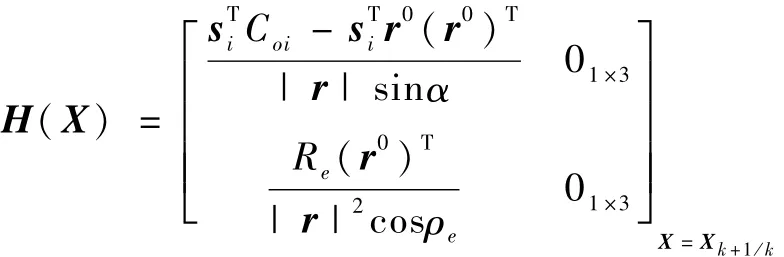
其中，r0为地心负方向矢量在卫星轨道坐标系下的投影，Coi为惯性系到轨道坐标系的转换矩阵，si（i=1，2，3）为第 i个恒星矢量。

应用EKF算法时，由于计算量不大，观测量的预测计算值可以采用非线性模型，因此yk+1的具体形式并不需要知道。在滤波计算中，观测量取3颗卫星的星光角距和1个地球视半径角，使观测矢量为四维，这样可以在尽量减少计算的基础上加快滤波收敛的速度。由于计算观测量的过程中需要知道地心矢量，而测量地心矢量的IRES的噪声比ST的噪声大很多，因此观测误差可以认为是IRES的测量噪声所致，其方差取为5×10-7（角度计算以弧度为单位，根据IRES的噪声得到）。

滤波过程使用EKF算法，具体算法如下

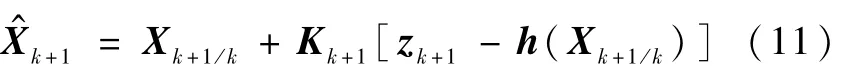
其中，计算预报值

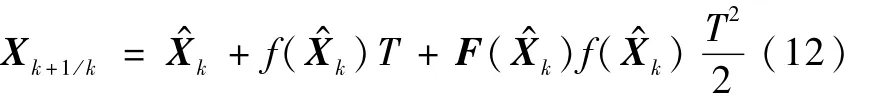
由于此处不涉及滤波中的矩阵运算，因此这里取为二阶以提高精度，其中的一阶导数。计算增益矩阵

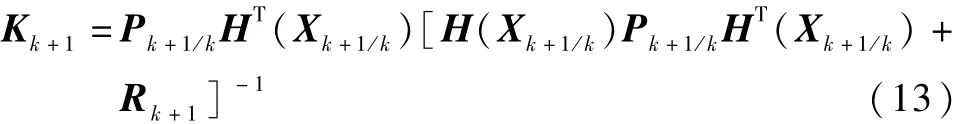
式中Rk为观测模型噪声的方差矩阵。计算预报方差阵

式中Qk为系统状态方程噪声的方差矩阵；计算滤波误差方差阵

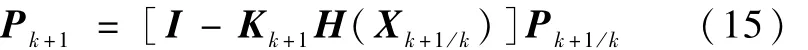
式中I为6×6的单位矩阵。

仿真过程中的计算过程如图4所示。

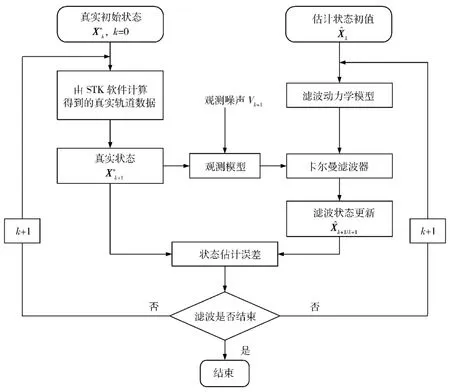
图4 卡尔曼滤波的仿真计算流程

3 仿 真

参考轨道参数为：轨道高度h=600 km；轨道倾角 i=97.5°；偏心率 e=0.001；初始条件 X=［6978140 0 0 0 -986.499 7493.205］T。本文的参考标称轨道是利用 STK（satellite tool kit）仿真软件，通过HPOP轨道预报器计算得到的。

（1）仿真中用到的敏感器精度模型

IRES噪声（3σ）：滚动≤0.042°，俯仰≤0.03°，编码分辨率为0.0055°（在对IRES进行地球辐射补偿和扁率补偿之后即可达到该精度）。

ST三轴姿态确定精度为18″（1σ）。

实际工程应用中会存在敏感器获取信息不同步或出现数据断续等情况，考虑这些因素，决定将仿真时间取为ST和IRES数据时间间隔的整数倍。另外，由于空间光照条件的影响，仿真中还考虑了敏感器间隔较长时间（如20 s）没有输出有效数据的情况。

（2）滤波周期和输出周期

仿真中设定系统的输出周期为 0.5 s，即每0.5 s给出一组轨道位置和速度参数。而滤波周期为系统进行一次滤波计算并对输出的轨道参数进行修正的周期，此周期与敏感器的输出频率有关。在敏感器无输出数据的情况下，按照简化的动力学方程进行递推，并将递推得到的轨道参数作为输出数据使用。

（3）仿真结果

若仅仅依靠动力学方程进行轨道递推，则计算得到的卫星位置和速度误差会迅速增大，这是由于卫星的动力学方程精度有限，导致每次轨道计算误差逐步累积，从而造成误差迅速增大。

图5和图6是采用本文提出的滤波算法，在采样周期为20 s和2 s时的三轴位置和速度误差。当采样周期为20 s时，三轴位置误差均小于100 m，速度误差均在0.5 m/s以内，且误差波动较大；当采样周期为2 s时，滤波稳定之后三轴位置误差均小于50 m，速度误差均在0.2 m/s以内。由此可知，适当减小采样周期，能够将滤波精度提高到较为满意的水平，而且在敏感器断续输出数据的情况下，系统也能够使用，不过输出数据的误差将会逐渐增大。

4 结 论

本文以低轨应用卫星为背景，充分利用现有星上敏感器，在不增加星载设备的情况下，通过两种光学姿态敏感器的测量，计算星光角距与地球视半径角，根据计算结果，采用 EKF的方法，修正轨道递推得到的轨道参数，从而实现卫星的自主导航。由仿真结果可以看出，近地卫星（轨道高度600 km左右）利用光学敏感器的自主导航技术，在滤波周期为2 s时，稳态情况下能够实现位置误差小于50 m、速度误差小于0.2 m/s的自主导航。同时，该技术对于短时间（文中仿真了20 s的情况）没有敏感器输出数据的恶劣情况，具有一定的适应能力。

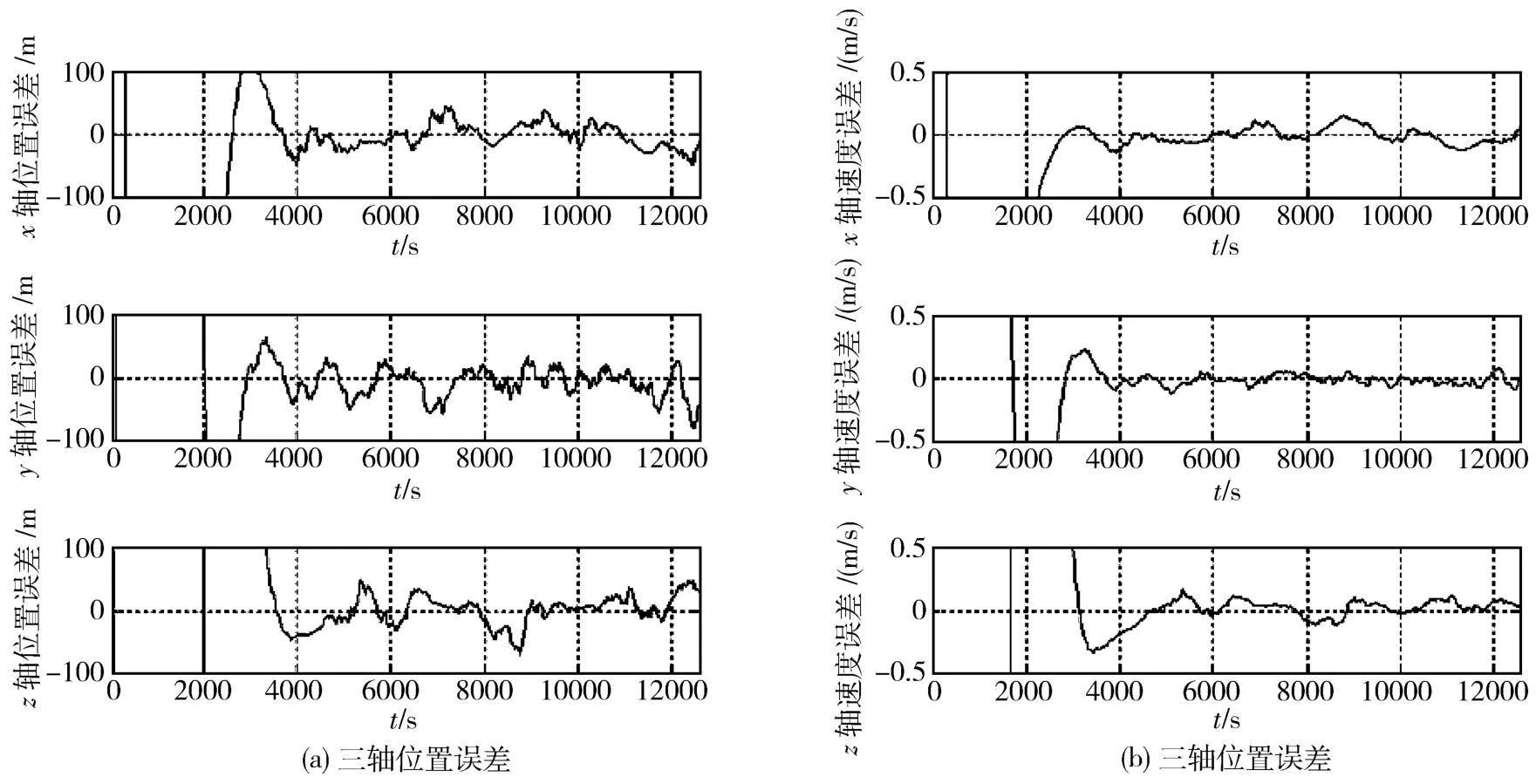
图5 滤波修正周期为20 s的导航结果

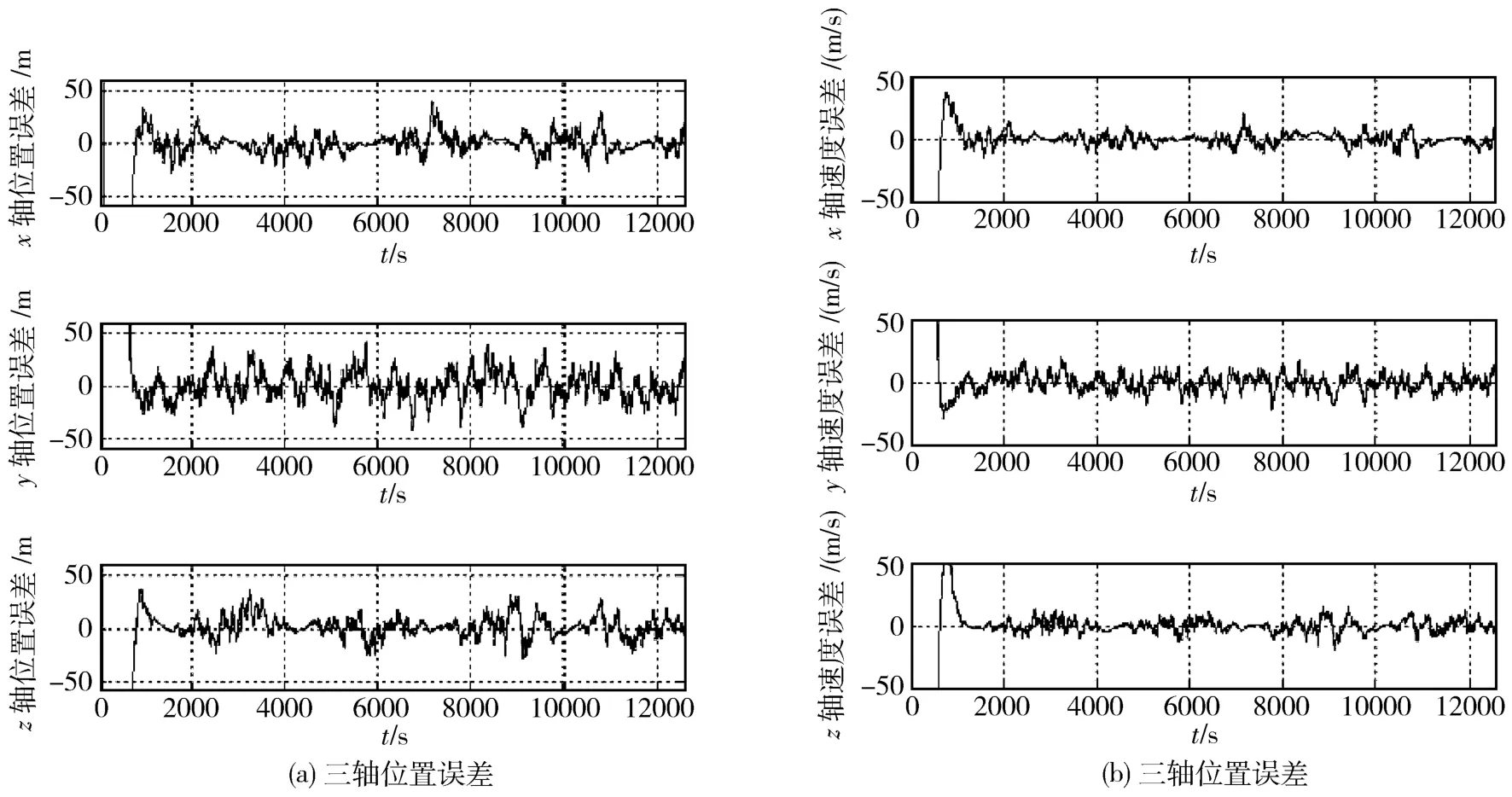
图6 滤波修正周期为2 s的导航结果

［1］ James R， Wertz J.Autonomous navigation and autonomous orbit control in planetary orbits as a means of reducing operations cost［C］.The 5thInternational Symposium on Reducing the Cost of Spacecraft Ground Systems and Operations，Pasadena，USA，2003

［2］ 潘科炎.航天器的自主导航技术 ［J］.航天控制，1994，12（2）：18-27

［3］ 赵黎平.近地卫星自主轨道确定和控制系统研究［D］.西北工业大学博士学位论文，2002

［4］ 刘林，胡松杰，王歆.航天动力学引论 ［M］.南京：南京大学出版社，2006

［5］ 章仁为.卫星轨道姿态动力学与控制［M］.北京：北京航空航天大学出版社，1998

［6］ Lefferts E J，Markley F L，Shuster M D.Kalman filtering for spacecraft attitude estimation［J］.Journal of Guidance Control and Dynamics，1982，5（5）：417-429

Autonomous Navigation for the Near-Earth Satellite Using the Optical Sensors

DU Yaoke，PENG Renjun
（Shanghai Aerospace Control Engineering Institute，Shanghai200233，China）

In this paper， a method of autonomous navigation for satellites based upon optical sensors' information is presented.This method makes good use of the attitude information acquired by the infrared earth sensor（IRES） and star tracker（ST） to calculate the star's angular distance and earth apparent radius angle，then the orbit elements deduced from orbit dynamics are corrected，so it is not needed to add other sensors to the satellite for the autonomous navigation purpose.An extended Kalman filtering（EKF）is used in the correcting process.After the system's state model and observation model are discretized and linearized，the EKF algorithm for the simplified model is deduced.Simulation results show that the convergence and accuracy of this method are very good.As no other sensors are needed for this method，the navigation method is potential for future use.

autonomous navigation；extended Kalman filtering；star tracker；attitude sensor

V448.22

A

1674-1579（2008）04-0055-05

2008-05-06

杜耀珂（1982-），男，上海人，助理工程师，研究方向为卫星姿态轨道控制（e-mail：dkexcellent@hotmail.com）。