一种高超声速飞行器的非线性再入姿态控制方法

张 军，毕贞法，邵晓巍

（1.上海宇航系统工程研究所，上海201108；2.上海交通大学空天学院，上海 200240）

一种高超声速飞行器的非线性再入姿态控制方法

张 军1，毕贞法1，邵晓巍2

（1.上海宇航系统工程研究所，上海201108；2.上海交通大学空天学院，上海 200240）

针对高超声速飞行器的再入非线性动力学模型，利用 SDRE（state dependent Riccati equation）设计姿态控制器。基于奇异摄动理论，把姿态动力学分解成姿态角和姿态角速度跟踪内、外环回路，同时把非线性动力学伪线性化。每个跟踪回路用SDRE获得控制律，考虑到SDRE局部渐近稳定的特点，可以保证系统闭环稳定。最后设计高超声速飞行器飞行控制系统，并在高超声速条件下进行仿真，验证了该方案的有效性。

高超声速飞行器；SDRE；非线性系统；姿态控制

1 引 言

目前，高超声速飞行器的控制系统设计采用了动态逆法，自适应滑模变结构，控制线性参数变化控制器和神经网络自适应扩展方法等［1-4］，它主要是通过非线性反馈和自适应等方法消除姿态动力学的非线性项，但这些方法很难克服输入约束和状态约束问题，尤其是目前广泛研究的动态逆法，其可调参数自由度小，往往无法获得期望的输入量。SDRE是近十年来设计的仿射非线性系统控制方法之一［5-8］，它采用的是非线性优化问题线性化设计，类似H2方法，具有鲁棒性，与状态相关的加权矩阵可有效折衷控制量和系统的动态性能。这种方法实现起来简单，目前已经有专门的数值解法［9］。

本文基于奇异摄动理论，针对高超声速飞行器再入高度非线性动力学模型提出SDRE解耦控制器内、外回路设计策略，利用SDRE局部渐近稳定的特点可保证系统闭环稳定。接着设计高超声速飞行器飞行控制系统，并进行仿真验证。

2 模型描述

面对称高超声速飞行器的无动力模型［1-2］为

式中，α、β和μ分别是飞行器的攻角、侧滑角和倾斜角；γ是弹道倾角；p、q和 r分别是滚动、俯仰和偏航角速度；Ixx、Iyy和 Izz分别是飞行器的主转动惯量，由于飞行器关于x-z平面对称，Ixz≠0；D、L和 Y分别是阻力、升力和侧向力，其中，（ρ为大气密度，V为飞行速度），CD、CL和CY分别为阻力系数、升力系数和侧力系数，它们是关于α和马赫数Ma的函数，Sref为飞行器的参考面积；l、m和n分别是滚动力矩、俯仰力矩和偏航力矩，由 RCS和气动舵面联合控制，Cl、Cm和Cn为滚动、俯仰和偏航力矩系数，它们是关于α、Ma、p、q和 r以及操纵舵 δα、δe和 δr的函数。

从式（1）可以看出，高超声速飞行器姿态动力学模型是时变非线性系统，与轨道参数耦合。飞行控制系统的设计实现三通道解耦，满足下述要求：α、β的控制精度保持在 ±1°以内；飞行过程中 β保持在 0°附近；舵面偏转饱和值为 δmax；p、q和 r要小于一定的约束值（总体要求）。

3 SDRE

控制领域内基于SDRE提出的仿射非线性系统的优化控制策略，简化了非线性 HJB（Hamilton-Jacobi-Bellman）方程的求解，避免了两点边值的约束问题。虽然理论上SDRE只是一种次优化控制，但其设计过程简单，计算量小，实时性强，广泛应用于非线性控制领域［5］。

对于非线性系统

考虑具有如下形式的无限时间性能指标：

在对酒店管理专业进行实践教学的过程中，教师可以采用角色扮演的形式，让学生在实践教学的过程中进行一定角色的扮演，在一定的场景之中来进行表演。

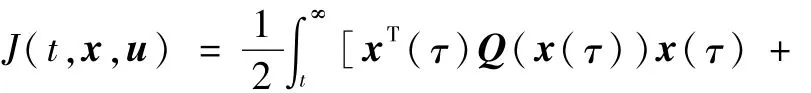
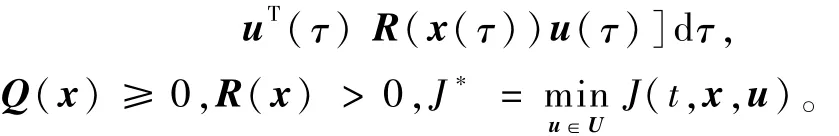
式中U是u凸约束集合，无限时间的非线性规划问题可以通过如下HJB偏微分方程求解

非线性系统直接求解方程（3）的过程复杂，计算量大，很难求得解析解。基于系统状态的Riccati方程可以看成线性LQR方法在非线性控制中的推广，将非线性方程写成基于系统状态的被控形式，并结合性能指标中的权值设计最优控制律，从而实现非线性系统的优化控制。将被控对象（2）转化为SDC（state dependent coefficient）形式

定义 1［5-6］.如果系统（2）满足（A（x），B（x））在状态域X内逐点可控，则称系统（2）可控。

引理 1［6-7］.对于一类仿射非线性系统（2），如果写成 SDC形式，f（x），g（x），B（x），A（x），Q（x），R（x）属于Ck，k≥1，并在原点领域内满足可控条件，则设计以下的优化控制律

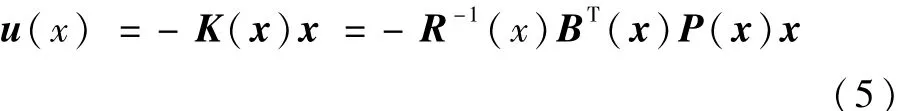
P（x）满足SDRE的正定解

使得闭环系统在原点领域内局部渐近稳定。

4 姿态控制方案设计

根据SDRE直接设计的一体化控制器非常复杂，参数调整难度大，计算量也大，难以在线应用［3］。

由于高超声速飞行器姿态动力学各状态变量的变化在时间上具有明显差异［2-4］，其中 α、β和 μ为慢变量，即对控制舵面或者 RCS的响应慢，频带在1～2 rad/s；p、q和 r为快变量，即对控制舵面或者RCS响应快，频带在5～10 rad/s。因此，在设计p、q和 r控制律时，可认为 α、β和 μ变量为常量。基于其存在明显时间尺度差异的特性，采用分阶控制的思想将飞行状态分为内、外环回路［3-4］，从内到外分别设计，简化了设计流程和复杂度。外环的输出p、q和r作为内环的输入跟踪指令。

将式（1）中的前三个方程转化为伪线性化SDC形式

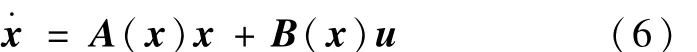
式中，x=［αβμ］T，u=［p q r］T，

而 A（x）和 B（x）中参数表达式分别为

由此看出，A（x）的选取并不唯一，但针对此方法的大量飞行仿真试验结果表明，不同的A（x），B（x）对系统的控制性能有影响，但影响较小［6］，只要要求在平衡点邻域内A（x），B（x）逐点可控即可。采用伪线性化模型建模可以避免在平衡点Jacobi线性化方法中带来模型误差，因为姿态动力学是高度非线性的，而这里只是等式变换。优化性能指标中的加权项直接影响闭环系统的动力学特性，对外环回路设计而言，要求跟踪性能好，控制量（角速度）小，满足角速度的物理约束。其他非线性方法（动态逆法）难以做到，若控制量过大，必须重新设计，较繁琐。SDRE可以直接有效折衷控制量和系统动态性能，通过试验的方法调整出合适的参数。仿真中，γ，m和 V近似不变。此外，对于有常值干扰的情况，可采用积分型SDRE消除静差。

快速变化的p、q和r的状态方程为

式中，x=［p q r］T，u=［l m n］T。这时主要以 RCS作为执行机构。当气动舵作为执行机构时，其形式复杂（包含气动力矩耦合），内环要求的动态响应比外环的快，这时要求控制量大，R（x）小，并满足力矩（或者舵机偏角）的物理约束，推导类似。

5 仿真研究

飞行器模型以及气动参数［1，10-11］如下：飞行器质量为 63503 kg，机翼参考面积 334.73 m2，V=3000m/s，γ=-3°。姿态仿真要求：α从 15°机动到0°，β从 8°机动到0°，μ从 20°机动 5°；p≤150（°）/s，q≤100（°）/s，r≤100（°）/s；采样周期为 10 ms，仿真结果见图1-6。从姿态角度调整来看，满足α、β保持在1°的精度要求，同时角速度没有超过物理约束。闭环系统状态的过渡时间和约束可通过内环和外环的加权矩阵进行折衷调节。

图1 攻角变化曲线

图2 倾斜角变化曲线

6 结 论

针对高超声速飞行器再入高度非线性动力学模型提出了SDRE控制器设计方法。基于奇异摄动理论，把姿态动力学分解成设计姿态角和姿态角速度跟踪内环和外环两个回路，并把非线性动力学伪线性化。每个跟踪回路用SDRE获得控制律，考虑到SDRE的局部渐近稳定的特性，可以保证闭环系统稳定。

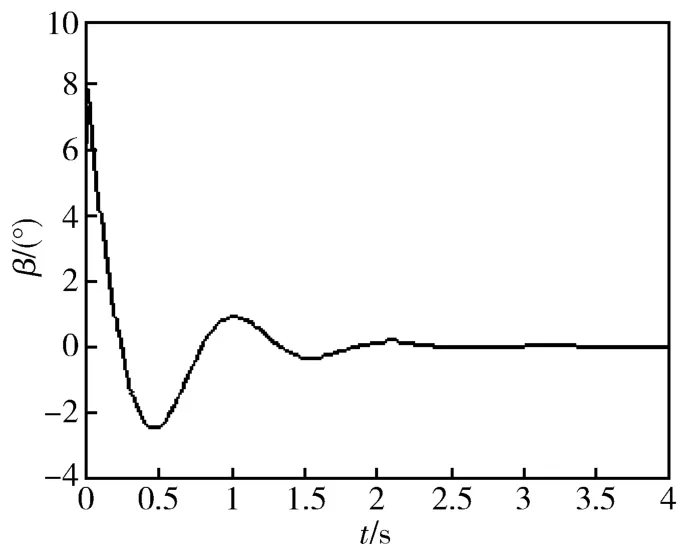
图3 侧滑角变化曲线

图4 滚动角速度变化曲线

图5 俯仰角速度变化曲线

图6 偏航角速度变化曲线

［1］ Socest W R.Combined feedback linearization and constrained model predictive control for entry flight［J］.Journal of Guidance，Control，and Dynamics，2006，29（2）：427-434

［2］ Snell S A.Nonlinear dynamic-inversion flight control of super maneuverable aircraft［D］.PhD Dissertation，University of Minnesota，USA，1991

［3］ Ning G D，Zhang S G，Fang Z P.Entry control using sliding modes and state observer synthesis for reusable launch vehicle［J］.Journal of Astronautics，2007，28（1）：69-76

［4］ 李扬，陈万春.高超声速飞行器 BTT非线性控制器设计与仿真［J］.北京航空航天大学学报，2006，32（3）：249-253

［5］ Evrin B，Erdem A G.Design of a class of nonlinear controllers via state dependent Riccati equations［J］IEEE Transaction on Control Systems Technology，2004，12（1）：133-137

［6］ Cloutiler J R.State-dependent-Riccati-equation techniques an overview ［C］.American Control Conference，New Mexico，1997

［7］ Cloutier J R，Souza C N，M racek C P.Nonlinear regulation and nonlinear control via the state-dependent Riccati equation technique［C］.International Conference on Nonlinear Problems in Aviation and Aerospace Daytona Beach，1996

［8］ Hammett K D，Hall C D，Ridgely D B.Controllability issues in nonlinear the state-dependent Riccati equation control［J］.Journal of Guidance， Control， and Dynamics，1998，21（5）：767-773

［9］ Cuo C H，Lancaster P.Analysis and modification of Newton's method for algebraic Riccati equations［J］.Mathematics of Computation，1998，67：1089-1105

［10］ John D S.Hypersonic vehicle simulation model：winged-cone configuration［Z］.NASA Technical Memorandum 102610，1990

［11］ Shahriar K.Six-DOF modeling and simulation of a generic hypersonic vehicle for conceptual design studies［C］.Modeling and Simulation Conf.2004，AIAA 2004-4805

A Non linear Entry Attitude Control Method for Hypersonic Vehicles

ZHANG Jun1，BIZhenfa1，SHAO Xiaowei2
（1.Aerospace System Engineering Shanghai，Shanghai，201108，China；2.Institute of Aerospace Science and Technology，Shanghai Jiaotong University，Shanghai，200240，China）

A controller is designed using the state dependent Riccati equation theory for nonlinear reentry attitude dynamics of a hypersonic vehicle.The dynamics is separated into fast and slow loops as attitude angular and attitude angular velocity based on the singular perturbation theory，simultaneously，the nonlinear attitude dynamic equations are pseudolinearied based on the state dependent coefficient.Each loop gets the dynamic control law by solving optimal SDRE.The characteristics of SDRE theory guarantee closed-loop systems to be stable.Finally，the flight control system of re-entry vehicle under hypersonic re-entry is designed by the proposed method.Simulation results demonstrate effectiveness of the method.

hypersonic vehicle； SDRE； nonlinear system；attitude control

TP 273.4

A

1674-1579（2008）04-0051-04

2008-03-05

张军（1972-）男，黑龙江人，副研究员，研究方向为模型预测控制（e-mail：zhangjun-jun320@sohu.com）。