基于全场Gamma系数的相位误差校正

摘要：面结构光由于可无接触对物体进行高质量的三维重建，目前已被广泛地应用在工业、医疗、文物保护等领域。工业领域中目前多以多频外差和格雷码+四步相移的编码结构光作为解决方案。采用单目多频外差方法， DLP的Gamma效应则会导致解算出的点云产生周期性误差。提出了一种全场Gamma系数校正的方法，可有效去除点云的周期性误差。通过搭建的实验平台对标准球进行测量，本文提出的方法有效地降低点云的周期性误差，球的标准偏差由0.0469mm降低至0.0183mm，球径误差均保持在0.02mm内。

关键词：面结构光；多频外差；Gamma；dlp；最小二乘

一、前言

面结构光通过向被测物体投射一系列编码光栅，并根据事先的标定数据以及解码信息，从而实现对被测物的三维重建。面结构光由于其非接触、高精度等特点目前广泛地被应用于汽车制造、口腔扫描、逆向工程等领域中[1-2]。

主流的面结构光解决方案多以相移光栅为主，主要有三频三相、三频四相、格雷码+四步相移等。若采用双目结构解算点云，最终的绝对相位信息只用来进行匹配，无需考虑相位误差；若采用单目结构解算点云，相位信息则会参与点云解算，相位误差则会造成最终的点云具有周期性误差，呈波纹状。本文主要对Gamma校正进行研究，降低相位误差，从而解决点云中的周期性误差问题。

在单目结构光中，DLP的Gamma值不为1的话，则会使投射灰度值与最终采集得到的灰度值呈一个非线性的关系，无法满足光栅的正弦性要求，从而使得相位解包裹时产生误差，并影响最终的绝对相位以及点云数据。

目前针对相位误差的补偿方法主要可以分为两大类：主动法与被动法。主动法是指通过计算出相应的Gamma系数，并对投影图案进行校正来保证光栅的正弦性。Baker等人[3]利用前馈反向传播神经网络的泛化和插值能力，对强度响应函数进行建模，并绘制从畸变条纹到非畸变条纹的映射图。Guo等人[4]使用边缘图像的归一化累积直方图来估计伽马值。Liu等人[5]建立了一个预测伽马畸变对标准相移

轮廓术（Phase Shifting Profilometry，PSP）影响的数学模型。利用PSP的谐波强度调制系数和大量相移模式估计Gamma值。Li等人[6]还将投影仪散焦并入Liu的模型[5]中，并通过使用两个预设的伽马值来确定散焦水平。Hoang等人[7]通过求解理想相位和畸变相位的非线性函数来确定伽马值，通过大量步移相来确定理想相位。Lei和Zhang[8]通过散焦二元条纹图生成准正弦条纹图来抑制相位误差。

被动法则不需要对投射图案进行校正，将采集到的图像数据进行一些后处理的算法操作来进行相位误差补偿。Zhang和Huang[9]提出了一种基于查找表（Look Up Table，LUT）的方法，在不使用任何数学Gamma模型的情况下直接补偿相位误差。LUT是根据投影仪的伽马校准计算出的相位误差来建立。Zhang和Yau[10]提出了另一种基于LUT的相位补偿算法，该算法的优势是适用于任何相移方法，无需标定投影仪的Gamma系数，根据在光滑平板上采集的条纹图像直接进行分析建立误差表。Pan等人[11]提出了一种基于非线性相位误差周期等于捕获条纹图相移次数的迭代相位补偿算法。

本文与其他方法的最大区别为本文中的Gamma系数并非为一个单一的固定值，而是每个图像中的每一个像素对应一个Gamma值。实际测量中，较难用一个Gamma值去描述整幅测量图像，本文通过建立理论图像与投射图像之间的关系，建立了相应的等式关系，并通过利用对数关系将指数关系转化为线性关系，从而利用最小二乘精确求解出图像中每个像素点所对应的Gamma系数。在求解出相应的Gamma系数后，根据相邻像素Gamma系数变化较小的特性，采用固定阈值区间来去除异常的Gamma值。针对图像边缘处像素Gamma值缺失的情况，采用了二次曲线进行插值，从而获得全场的Gamma值。

实验结果表明，使用本文提出的方法可有效地计算出全场像素所对应的Gamma系数，并用搭建的单目结构光系统，对一个标准球进行了测量，进行Gamma校正后球拟合的标准差由0.053mm降低至0.021mm，球径误差均保持在0.02mm内，证明了本文方法的有效性。

二、原理及数学模型

（一）Gamma系数数学模型

在一个暗室情况下，即无环境光干扰，可得到以下的公式：

（1）

上式中，I_c表示相机采集的图像，I_p表示理论投射灰度，α表示缩放系数，γ表示Gamma系数。

若有多组数据，则可以得到以下关系：

（2）

将上式中相邻两组数据做除法运算，并取对数可得：

（3）

上式中只有γ为未知数，则可设：

（4）

故可得n-1个误差方程式：

（5）

根据误差方程使用最小二乘进行求解γ，最终的解为：

（6）

（二）固定阈值区间去异常值

本文中针对单个像素计算每个像素所对应的Gamma系数，如存在噪点，则会使计算出的Gamma值呈现异常，异常的Gamma值则会使校正像素值出现异常，从而影响最终的解算。

考虑邻近区域的Gamma值较为接近，不存在Gamma值差异较大的情况，将中心点与阈值进行比较，若不在阈值区间内，则视为异常值，剔除，并用双线性插值计算相应的Gamma系数。因原理较为简单，故不再赘述。

（三）二次曲线插值

当dlp投射的图案没有占满整个CCD采集的图像时，则无法保证所有像素都含有相应的Gamma系数。缺失相应的Gamma系数则会无法保证在实际应用中解算出的点云具有全场的精度一致性。故需要进行相应的插值操作，以保证所有像素都有对应的Gamma系数。

本文采用二次曲线插值的方法对缺失Gamma系数的像素进行插值。首先对行上的像素进行Gamma系数计算，二次曲线的公式如下：

（7）

x表示像素的x方向坐标值，f（x）则表示每个相应坐标的Gamma系数，a，b，c则表示二次曲线的系数，为待计算系数。

本文中认为相邻的Gamma系数变化较小，采用局部拟合的方式进行二次曲线拟合。首先在行中进行搜索，若五个相邻像素点中有一个像素点缺失，则利用其余四个点进行二次曲线拟合，求解相应二次曲线系数，然后计算出缺失像素的Gamma系数。求出行方向二次曲线系数abc即可完成插值。行方向计算完成后再沿列方向进行相应的操作，即可完成Gamma系数的全场覆盖。

三、实验及结果

（一）实验步骤

根据推导的最小二乘Gamma系数求解式（6），只需提供每张图像中对应像素点的灰度值，即可进行求解。

本文的实施方案如下：

（1）在一个暗室环境下向一块白板投射一系列纯色灰度图像，灰度值为0-255，采样间距为5，投图期间设备保持静止；

（2）利用式（6）计算每个像素的Gamma系数；

（3）采用中值滤波去除异常Gamma值；

（4）边缘部分无Gamma值则采用。

（二）实验

本文选取了海康MV-CA013-21UM型号的相机，镜头为浩蓝的12mm镜头，腾聚DLP3000型号的光机，搭建了如图1所示的单目结构光系统。

在最佳工作距处向一白色平板分别投射灰度值为0，5，10，…，255的纯色灰度图，采集得到的图像如图2所示。

按式（6）计算出的Gamma系数，并经过固定阈值区间去异常值后的结果如图3所示，采用二次曲线插值后的全场Gamma系数如图4所示。

向一光滑白板投射频率为1的四步相移的正弦光栅。将采集的数据直接解包裹，在将采集的数据进行Gamma校正后进行解包裹，取图像中的第500行进行比对，可以清晰地看出误差降低有着明显的降低。

四、实际应用

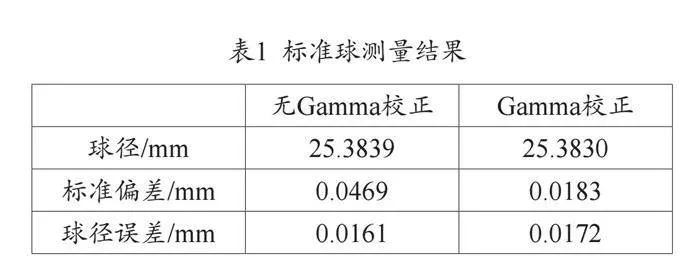
采用本文所搭建的单目结构光系统，采用三频四相的正弦光栅对一个标准球进行了测量，标准球的直径为25.4mm。测量结果如表1所示。

在进行Gamma校正后，球的表面明显变得更加光滑，这直接体现在表1中的拟合球的标准偏差上，由0.0469mm降低至0.0183mm，有了较为明显的提升。相对比下，球的直径误差都保持在0.02mm内，精度较高。同时验证了本文所提出方法的有效性。

五、结语

本文所提出的方法只需在测量前向一白板投射一系列纯色灰度图，采用最小二乘法即可计算出大部分像素对应的Gamma值。再通过固定阈值区间去异常值及二项式插值即可得到全场像素对应的Gamma值，从而可以对采集的数据进行Gamma校正。在球径误差基本不变的情况下，球的标准偏差由0.0469mm降低至0.0183mm，验证了本文所提出的方法的有效性。

本文所提出的方法未考虑环境光的影响，实验中环境光影响较弱，下一步需考虑环境光的影响，并进行相应的实验，以提高该方法的实用性。

参考文献

[1]李绒.面结构光三维系统相位测量精度研究[D].成都：电子科技大学，2017.

[2]赵必玉. 高精度面结构光三维测量方法研究[D].成都：电子科技大学，2015.

[3] Baker M J ， Xi J ， Chicharo J F.Elimination of Non-linear Luminance Effects for Digital Video Projection Phase Measuring Profilometers[C]//Electronic Design， Test and Applications， 2008. DELTA 2008. 4th IEEE International Symposium on.IEEE， 2008.

[4] Hongwei G ，Haitao H ，Mingyi C .Gamma correction for digital fringe projection profilometry[J].Applied optics，2004，43（14）：2906-14.

[5] Kai L ，Yongchang W ，L D L ， et al.Gamma model and its analysis for phase measuring profilometry[J].Journal of the Optical Society of America. A， Optics， image science， and vision，2010，27（03）：553-62.

[6] Zhongwei L ，Youfu L .Gamma-distorted fringe image modeling and accurate gamma correction for fast phase measuring profilometry[J].Optics letters，2011，36（02）：154-6.

[7] Thang H ，Bing P ，Dung N ， et al.Generic gamma correction for accuracy enhancement in fringe-projection profilometry[J].Optics letters，2010，35（12）：1992-4.

[8] Shuangyan L ，Song Z .Flexible 3-D shape measurement using projector defocusing[J].Optics letters，2009，34（20）：3080-2.

[9] Zhang S ，Huang S P .Phase error compensation for a 3-D shape measurement system based on the phase-shifting method[J].Optical Engineering，2007，46（6）：063601-1-063601-9.

[10] Song Z ，ShingTung Y .Generic nonsinusoidal phase error correction for 3D shape measurement using a digital video projector[J].Harvard Univ. （United States），2006，629262920R-62920R-10.

[11] Bing P ，Qian K ，Lei H ， et al.Phase error analysis and compensation for nonsinusoidal waveforms in phase-shifting digital fringe projection profilometry[J].Optics letters，2009，34（04）：416-8.

作者单位：未来宇航（上海）航天科技有限公司

责任编辑：张津平 尚丹