利用随机收集数据，促进生成意识形成

一、教材及学情分析

平均数是统计学中一个常用的统计量。北师大版教材把平均数知识安排在四年级下册“数据的表示和分析”部分，明显加重了平均数的意义在数据的表示和分析中的分量，突出了平均数的统计学意义，即平均数能表示统计对象的一般水平。它是描述数据集中程度的一个统计量，既可以反映一组数据的总体情况，又可以作为不同组数据相比较的一个标准，可以看出组与组之间的差别，所以平均数是统计中的一个重要概念。本节课是学生进一步学习平均数在统计学中的作用的基础，也是学生学会对一组数据进行分析、描述的关键。

二、教学目标

1.结合解决问题的过程，了解平均数的意义。

2.能结合简单的统计图表，解决一些简单的与平均数有关的实际问题。

3.进一步积累数据分析的活动经验，培养生成意识。

三、教学重难点

教学重点：会用平均数解决问题，提高解决问题的能力，形成生成意识。

教学难点：体会平均数能较好地反映一组数据的总体情况。

四、教学策略

启发式教学法。

五、教学过程

（一）设疑导入

师：一天，淘气的爸爸带他去玩，路过一个小池塘。淘气不会游泳。他看到池塘边上的一个警示牌写着：平均水深1.1米。淘气的爸爸问：“你如果不小心掉下去，会不会被淹呢？”淘气说：“我身高已经1.4米了，超过水深了。我掉下去肯定不会被淹的。”你同意他的观点吗？为什么？

生：我同意他说的，身高超过平均水深肯定不会被淹了。

生：我觉得还得看池底是否光滑或有淤泥。如果池底很滑，那淘气下去后站不住，滑倒了，或者陷进去，就有可能被淹。

生：我不同意他说的。我认为池塘的底部不一定平整，有深有浅，遇到深的地方就有可能被淹到。

师：到底谁说得有道理呢？请注意警示牌上写的是“平均水深”，像平均水深、平均分、平均温度、平均年龄等都是平均数，今天我们就来一起研究平均数的有关知识。通过对平均数的研究，我们就知道在这种情况下淘气会不会被淹到了。（板题：平均数）

（设计意图：通过设疑导入，有效激发学生的数学思考和探究欲望，为深入学习本课新知打好基础。）

（二）探究新知

▲活动一：竞技游戏，收集数据

师：老师带来一个竞技性非常强的游戏，叫“记数我最强”。

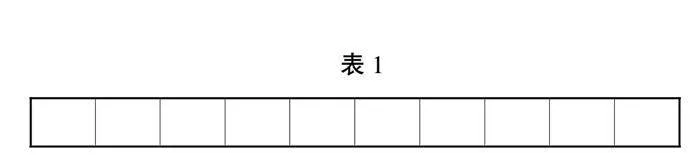
教师利用课件出示游戏规则：课件每3秒自动呈现10个数字。大家心里默记。当数字消失后，请你在10秒内把记住的数字按顺序记录在表中（见表1）。当数字再出现时，按照上面的规则记录数字，并记录记对了几个数字。

师：（课件出示一串数字）先默记3秒，然后按顺序写出你刚刚默记的数字，时间10秒。

师：快数数看你记对了几个。

生：7个。

生：8个。

师：刚才有些同学记得没那么好。那我们就再玩一次吧，请看屏幕。（继续按规则呈现数字。）

师：这一次你又记住了几个呢？

生：8个。

生：9个。

师：还想再继续挑战吗？好，满足你们，那就再玩一次吧，看看你们能不能破你们自己的记录。

（师生再一次玩记数字游戏）

师：大家对这三次的游戏结果满意吗？那么，下一次有没有信心会记对呢？

生：有信心。（话语中显得底气不足）

师：来吧，再玩最后一次，看看能不能挑战胜利。

（师生再一次玩记数字游戏）

师：玩了四次游戏，老师现在想请同学们把这四次的记数情况写在黑板上，谁乐意上来写呢？请你来说，我来写。

生：6、4、7、5。

生：6、7、5、8。

（设计意图：变教材中静态的数据为动态的游戏。一方面，增添课堂教学的趣味性，提高学生的学习兴趣和学习效果；另一方面，现场动手收集数据突出体现了数据收集的真实性。学生亲身经历数据产生、收集、整理和统计的全过程，彰显了统计的本质。这样学生能够较好地体会平均数的意义，形成初步的数据意识。）

▲活动二：引发冲突，感悟平均数

1.通过问题引发认知冲突，体会平均数的意义

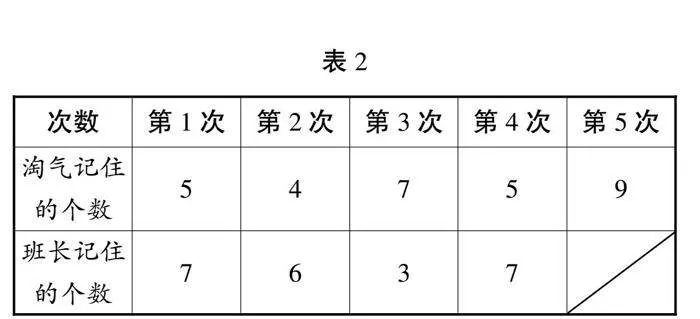
师：（课件出示淘气五次和班长四次的记数情况表，见表2）比一比，看一看，他们两个人记住的数字总数不一样，次数也不一样，那么谁的记忆能力更强一些呢？

生：我觉得淘气的记忆能力更强一些，因为淘气记住了30个数字，而班长只记住了23个数字。

生：我觉得淘气的记忆能力更强一些。因为淘气最少的一次是记住4个数字，而班长是3个。

生：我有不同意见，我觉得班长的记忆能力更强一些，因为在前四次中，班长有三次记住的数字个数都超过了淘气，所以我认为班长的记忆能力更强一些。

生：我觉得应该是淘气的记忆能力更强一些。因为淘气最多一次记住9个数字，而班长最多才记住7个数字。

生：我觉得班长的记忆能力更强一些，因为班长有两次都是记住7个数字，而淘气有两次记住5个数字，所以我认为班长的记忆能力更强一些。

师：大家的发言像是一场辩论赛，说明大家都在积极动脑筋思考，这是非常好的现象。好像都有道理。那到底谁的记忆能力更强一些呢？这就需要我们正确理解“平均数”这个概念和意义了。刚刚大家的发言里体现了大家对“平均数”概念和意义的理解。究竟应该怎样正确理解呢？

（设计意图：通过现场记数游戏，学生会主动思考，想方设法比较谁的记忆能力更强。学生的回答就体现了他们对“平均数”概念和意义的理解情况。这就准确了解了学情，在接下来的教学活动中才能有针对性地设计活动，帮助学生理解“平均数”的概念和意义。）

2.实际操作，理解“平均数”

师：根据刚才的回答，我们很难区分出谁的记忆能力更强。那么，我们能不能用一个数字代表他们两个人各自的记忆能力呢？

师：由统计表你们能看出淘气能记住几个数字吗？淘气平均每次记住数字的个数用几表示比较合适？

出示智慧老人的说法：淘气平均每次记住6个数字。

师：“平均每次记住6个数字”就是这5次平均每次记住的数字的个数同样多，都是6个。但是淘气这5次没有一次记住6个数字呀，你们想知道这个数字“6”是怎么得来的吗？

学生小组内操作：摆一摆或画一画，使5次同样多。

学生操作后汇报。

生：因为第5次和第3次记住数字的个数比较多，所以第5次给第1次1个，给第2次2个，第3次给第4次1个，这样淘气每次记住数字的个数就都变成了6。

师：大家认为他说得有道理吗？

生：非常有道理。

师：我觉得说的没有演示的清楚。那么，谁愿意到黑板上演示一下呢？一个小圆片代表记住的一个数字。

学生上台演示。

师：像刚才这位同学演示的那样，通过把多的移动补给少的，使每次记住数字的个数同样多，这种方法就是“移多补少”法。用这种方法可以求出淘气5次平均每次记住数字的个数。那么，这个6就出现了。大家觉得用6代表淘气记忆的平均水平合适吗？

生：非常合适。

师：除了这种方法，还有其他的方法吗？

学生讨论后汇报。

生：先把这5个数合起来，再平均分。

师：“合”就是把这5个数加起来，然后平均分成5份，每一份就是平均数。

（1）总结算法

（5＋4＋7＋5＋9）÷5

＝30÷5

＝6（个）

（2）分析算式

我们把5＋4＋7＋5＋9的和称为总数量，5称为总份数，所得的6就是平均数。通过刚才的计算我们可以得出一个关系式：总数量÷总份数＝平均数。

师：可以用“移多补少”法来求平均数，还可以用“算术”法求平均数，在掌握基本方法的同时，还要学会根据题目中的数据特点灵活选择算法，怎样简便就怎样算。

师：我们现在已经了解到了“移多补少”和“算术”法求平均数的方法，那么，这两种方法有什么相同的地方吗？

生：相同之处就是总数都一样，最后得到的结果也都一样。

生：相同之处就是都含有均分的过程，也就是不同数量之间互相匀一下，最后达到都相等。

师：有个字说得太好了，大家听出来了吗？

生：分。

生：匀。

师：对，就是“匀”字。平均分其实就是匀的过程，平均数就是匀出来的。这个6就是淘气5次记住的数字数匀出来的，它就代表淘气这5次记忆的平均水平。

师：平均水平是不是哪一次的水平呢？

生：不是的，是某几次的平均水平。

师：是的，平均数是一组数据的平均水平。

▲活动三：感知内涵，深入理解

1.问题思考，促使学生进一步理解平均数

师：平均数代表的是一组数据的平均水平，那么，平均数是这一组数据中的数字吗？现在同桌两人一组进行讨论，讨论后进行汇报。

生：一组数据中有可能有平均数的那个数字呀，比如淘气5次记住的数字数中，如果恰好有一次是6个，平均数正好也是6，那么，这个平均数就是这一组数据中的某一个数；而书上给我们的数据中，淘气没有一次记住6个数字，恰好平均数又是6，那么，这时平均数就不是这一组数据中的数。

师：是的，平均数是匀出来的。匀出的这个数字有可能跟这一组数据中的某个数字一样，也有可能不一样。所以，并不是一组数据中的某一个数都可以代表这组数据的平均水平，它有可能在这个数据之外。

（设计意图：利用问题引发学生深度思考，促进学生进一步理解平均数的内涵，增强学生对平均数的深度理解。）

2.利用实例，形成生成意识

利用生活中的实例展开教学，有助于学生根据数据预测、判断、推理等生成意识的形成。

师：同学们，请你们想一想，在我们生活中哪里还藏着平均数呢？看谁找得快、找得准？现在开始。

生：我们班数学期中考试的平均分。

生：我们本地夏季的平均温度，或者某一天的平均温度。

……

师：说得太好了。我们身边蕴藏这么多平均数呢，只要我们积极动脑、善于发现，就可以找到很多平均数。

师：淘气班这次的数学平均分是90分，你觉得淘气考了多少分呢？

生：90分。

师：大家同意吗？

生：不同意。因为淘气考的分数不一定正好是平均分，只能说有可能是90分。

生：淘气考多少分都有可能，因为平均分是匀出来的。他考的分数有可能低于90，有可能高于90，也有可能等于90。我觉得有这三种情况。

师：是的，淘气的分数有这三种可能，不一定正好是90分。

师：一组数据如果再加上一个比平均数小的数字，那么这一组新数据的平均数就比原来的平均数小；如果加的这个数与原来这组数据的平均数相等，那么这一组新数据的平均数还和原来相等；如果加的这个数字比原来这组数据的平均数大，那么这一组新数据的平均数就比原来这组数据的平均数大。

师：请大家思考一下，平均数的大小受哪些因素的影响？

生：受总数和总个数的影响。

生：受特殊数值的影响较大。

师：请你具体说说什么是特殊数值，受到怎样的影响。可以举例说明。

生：我所说的特殊数值就是较大的或较小的数值。比如，我们班的数学平均分就受成绩很差和很好的影响较大。如果这学期来个数学成绩很差的学生，那么我们班的数学平均分就会降低很多；如果来个成绩很好的学生，那么数学平均分就会上升。

师：说得很好。在一组数据中加上一个很小的数，这组数据的平均数就会下降，如果这组数据的个数越少，下降的幅度就越大；相反，平均数就会上升，甚至上升幅度很大。

（设计意图：通过让学生寻找生活中的平均数，引导学生感知平均数就在我们的生活中。然后，通过实例让学生经历根据数据信息预测、推断和推理等对事情进行研判和决策的过程，促进学生形成生成意识，捕捉生活中“从无到有”的信息，发现信息背后的信息。）

（三）巩固练习

1.在1分钟跳绳训练中，笑笑四次的成绩分别如下：85下、87下、86下、86下，用什么数表示笑笑的成绩最合适？这个数是多少？

2.佳佳和依依分别在四年级的两个班。佳佳班的数学期中考试平均分是88.6分，依依班的数学期中考试平均分是85.3分。淘气说佳佳的这次数学期中考试分数比依依高。你同意他的观点吗？为什么？

（设计意图：检测学生对平均数的理解以及利用平均数解决生活中问题的能力，巩固学生生成意识的培养。）

（四）课堂小结

1.用自己的话说说你对平均数的认识。

2.通过今天这节课的学习，你有什么想说的呢？

（设计意图：利用问题引导学生说出这节课的收获，检测学生的学习效果和教师的教学效果。同时，引导学生归纳总结本课所学知识。）

（五）布置作业

收集小组每个成员的体重，并整理成统计表，再求出小组成员的平均体重。根据每个成员的体重与小组成员的平均体重，你想对各个成员说什么？

（作者单位：甘肃省定西市渭源县会川镇文峰中心小学）

编辑：常超波