考虑地铁列车控制的纵断面设计优化方法

摘要：地铁列车控制优化与纵断面设计关系密切，二者对运营费用有重要影响。为在列车控制优化的基础上进一步降低运营费用，在线路纵断面设计阶段构建了协同优化模型，考虑定时列车控制对纵断面进行优化，在满足定时列车控制约束、《地铁设计规范》要求等的前提下，最小化能耗成本和维修成本之和。由于车轮、钢轨维修成本的影响因素众多，建立列车-轨道动力学仿真模型计算维修成本，在此基础上设计综合伪谱法和蛮力搜索的算法求解协同优化方案，并应用于广州地铁线路的3个区间，对方法的优化效果进行验证。研究结果表明，对比在实际纵断面上单独优化定时列车控制的方法，同时优化定时列车控制方案和纵断面方案对节约运营费用的效果更佳，各区间运营费用平均降低21%。该研究方法可为进一步控制运营费用提供新思路和理论依据，推动地铁系统可持续发展。

关键词：地铁；列车操纵策略；线路设计；运营成本；伪谱法

中图分类号：U212.34""" 文献标志码：A""" 文章编号：1002-4026（2025）01-0105-15

开放科学（资源服务）标志码（OSID）：

DOI：10.3976/j.issn.1002-4026.20240062【交通运输】

收稿日期：2024-04-16

基金项目：国家自然科学基金（71571016）

作者简介：樊葱（1996—），女，硕士，助理工程师，研究方向为城轨线路设计。E-mail： cong19960922@163.com

Optimizing vertical track alignment considering metro train control

FAN Cong

（Guangdong Guangzhou-Zhuhai Intercity Railway Co.， Ltd.， Guangzhou 510422， China）

Abstract∶Energy-saving metro train control is closely related to the vertical track alignment （VTA） design， and both have a significant impact on operating costs. To further reduce operating costs based on optimized train control， this study proposed a collaborative optimization model for the VTA design phase. This model optimizes the bidirectional train control strategy and VTA of a metro section with the goal of minimizing energy consumption and maintenance costs simultaneously， while adhering to the constraints of scheduled train control and the requirements of the \"Metro Design Code.\" Given the numerous factors affecting the maintenance costs of wheels and rails， a train-track dynamic simulation model was developed to calculate these costs. Based on this， an algorithm combining the pseudospectral method and brute force search was designed to solve the collaborative optimization model. The effectiveness of this optimization method was validated using three sections of the Guangzhou metro line. The results indicate that， compared to the method of optimizing scheduled train control alone on the actual VTA， the collaborative optimization model is more effective in saving operating costs， reducing the average operating costs by 21% across the studied sections. This study can provide novel approaches and theoretical support to further reduce metro operating costs， which contributes to promoting sustainable development of metro.

Key words∶underground metro; train trajectory; track alignment design; operating cost; pseudospectral method

发展地铁具有方便市民出行、带动区域经济等优点，随着城市化进程持续加快，近五年地铁线路总里程增长约4 500 km［1］。地铁线路增长导致能耗成本问题突出，近五年地铁耗电量增长逾4亿度，其中50%～70%用于列车牵引［2］。另一方面，随着建成年限变长，更多线路进入维修期，维修成本不断增加，根据北京地铁数据，每公里的维修成本甚至超过了能耗成本。

为降低列车牵引能耗，节约能耗成本，地铁运营单位采取了优化列车控制、使用轻量化车辆等措施［3］，但这些措施的节能效果受线路条件制约。地铁线路主要包括线路平面和纵断面。平面方案设计更侧重于尽量多地吸引客流［4］，而非降低列车能耗。纵断面直接影响列车所受阻力，不同纵断面下的列车控制优化方案及能耗可能不同，而且以节能为目标优化纵断面时需考虑列车控制优化，因为最优纵断面方案可能随列车控制方案改变。所以，相比平面设计，纵断面设计与列车控制优化的关联更紧密，如果在设计纵断面时同步优化列车控制，相较仅优化列车控制方案，将更有助于节约能耗成本。

纵断面设计一般指在给定线路平面的条件下，确定满足实际约束的一系列坡道。Jha等［5］首先在设计纵断面时同时考虑降低建设成本和能耗成本，但假设能耗成本正比于列车运行距离，计算方法较为粗略。为精确计算能耗，Kim等［6］建立列车运动模型描述列车运行行为，导致模型的非线性化增强，当考虑更多实际约束时需使用更高效的算法求解。柏赟等［7］、彭磊等［8］相对全面地考虑了纵断面设计中的实际约束，并采用启发式算法快速求解模型，但解的最优性难以保障。徐杨［9］进一步设计蛮力搜索和动态规划相结合的算法求得问题的精确解，然而研究中列车采用节时控制策略，所求解不一定最适用于实际运营中给定运行时分下的列车控制。Hoang等［4］和Wu等［10］在已知运行时分的前提下，同时优化纵断面方案和列车节能控制方案，但可能受计算效率的限制，为缩小问题可行解规模，优化过程中纵断面设计形式保持不变，解的最优性无法确保。Duarte等［11］对算法进行改进，设计梯度优化法求解协同优化模型，但忽略了坡长约束等，可能导致所求方案无法在实际中应用。

除能耗成本外，不同列车节能控制方案和纵断面方案下，设备使用寿命通常存在差异，从而影响维修成本。汤超［12］、肖绯雄等［13］采用动力学仿真方法计算不同坡度、列车运行速度下的轮轨、闸瓦磨损量，证明在其他条件不变的前提下，轮轨和闸瓦磨损量随坡度绝对值或列车运行速度增大而增加。Lai等［14］在优化纵断面和列车控制时考虑了节约维修费用，但维修费用仅正比于运行距离，未考虑不同设备间维修成本的差异。Kang等［15］分别根据车轮、钢轨等设备的年维修费用计算各维修成本，再以所有设备维修成本及能耗成本最小为优化目标，求解最优纵断面方案和列车控制方案，但仍未较精准地量化不同方案对维修成本的影响。

在更精准化不同方案对维修成本影响的基础上，本文考虑定时列车控制对纵断面进行优化，提出基于列车-轨道动力学仿真的地铁区间纵断面设计和列车节能控制协同优化方法，该方法尽可能全面的考虑定时列车控制约束和《地铁设计规范》［16］等要求，采用伪谱法和蛮力搜索的算法，在保证求解精度的前提下高效求解优化方案，以最小化能耗成本和维修成本。

1" 考虑列车控制的纵断面优化问题

截至2022年底，全国城市轨道交通中69%以上线路为地下线［1］，地铁中地下线占比更高，广州地铁达88%左右，多数使用盾构法建设。此时，建设费用基本取决于线路长度，由平面方案决定［17］。由于在纵断面设计阶段，平面方案一般已提前确定，不同纵断面方案下的线路长度及相应的建设成本差异很小。因此，通过优化地下线列车控制方案和纵断面方案，可以在不改变建设成本的前提下降低能耗成本和维修成本，达到减少总成本的目的。

对于地下线车站，其水平位置由平面方案给定，高程一般按尽量接近地面以方便乘客进出站的原则确定，车站的空间位置可视为已知条件。此时，当仅考虑一般的运营模式，列车在各站均停车，任意两相邻车站间的列车控制和纵断面优化与其他区间互不干扰，各区间可单独进行优化。为提高问题的求解效率，以下对单个区间上考虑列车控制的纵断面优化问题进行研究，当全部区间都使用该方法，即可得到全线优化方案。

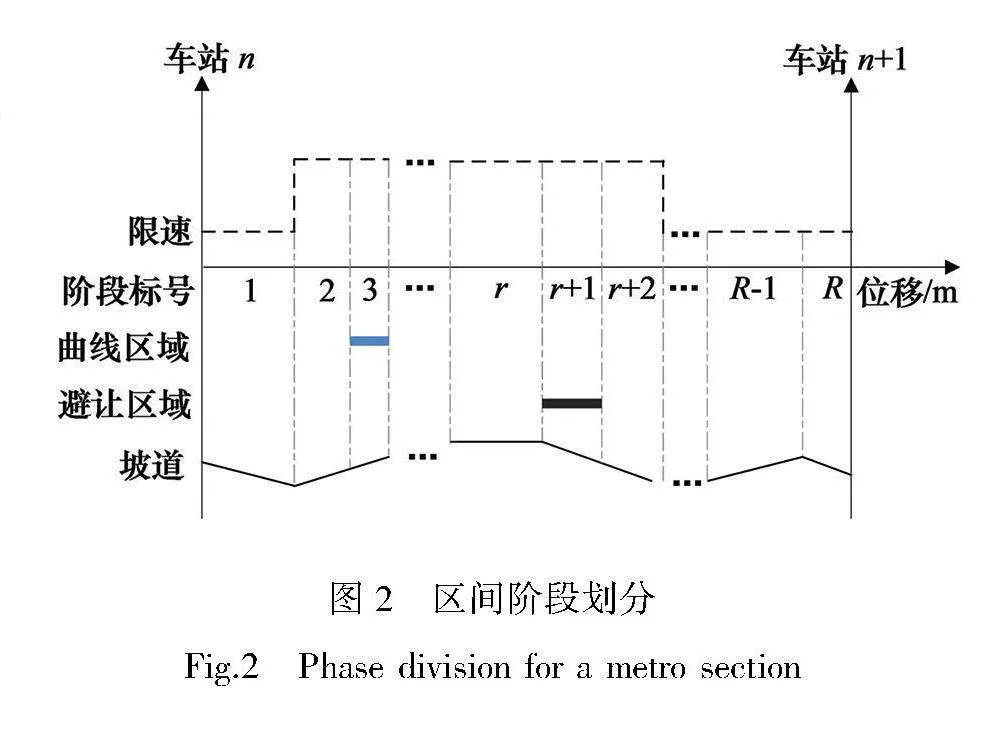
第n个区间纵断面设计示意图如图1所示，一般情况下，上行和下行方向轨道敷设在同一隧道中，纵断面呈对称关系，不同方向上的最优列车控制方案可能存在差异。若协同优化仅以降低一个方向的列车牵引能耗为目标，可能使另一方向的列车牵引能耗较大，不利于节约总能耗成本。因此，计算能耗成本时考虑双向牵引能耗。

由于地铁系统复杂、设备众多，维修成本仅考虑与纵断面方案、列车控制方案密切相关的重要设备，主要有闸瓦、车轮和钢轨。当各设备单次平均维修成本一定，在相同时间内，总维修成本由各设备使用寿命决定。闸瓦、车轮和钢轨使用到限的主要原因是摩擦磨损［18］，所以维修成本为修理、更换因摩擦磨损使用到限闸瓦、车轮和钢轨的人工成本和材料成本。虽然设备磨损量还受轨道结构影响，但在实际中，轨道结构设计主要考虑减振降噪［19］，而非减少设备磨损，在研究中视为已知条件。

为最小化能耗成本和维修成本之和，对纵断面方案和列车定时控制方案进行协同优化。其中，纵断面可由各坡度和坡长、连接相邻坡道的竖曲线表示。由于竖曲线位于相邻坡道交汇处，且曲线半径按设计规范要求取值，决定纵断面方案的关键因素为各坡度和坡长。在给定的线路上，列车定时控制方案由牵引力和制动力决定。优化方案同时受定时列车控制约束、《地铁设计规范》要求和实际工程约束等限制，具体将在模型部分进行介绍。

2" 协同优化模型构建

对于协同优化问题，线路条件及部分参数如限速和避让区域都随位移发生变化，将这些变量称为位移关联参数。为简化问题中对位移关联参数的表示，将区间按一定规则划分为多个阶段，构建多阶段优化模型，以提高求解效率［20］。阶段划分如图2所示，首先将每个曲线区域和避让区域都设为单独的阶段，再按同一阶段内坡度和限速都相同的原则进行划分。由于限速、曲线和避让区域位置为已知值，确定各坡道长度后，即可获得阶段划分方案。

2.1" 模型假设

模型假设如下：

（1）研究表明，再生制动能利用与纵断面设计关联较小［6］，本文计算能耗成本时暂不考虑再生制动能；

（2）假设运营单位对设施设备状态进行定期监测，能够及时更换磨损到限的设备，且不考虑单次平均维修成本定价问题，其不因设备维修次数等发生改变；

（3）相比轮轨在曲线上的磨损，其在直线上的磨损非常小［21］，因此只考虑轮轨在曲线上的磨损，且同一列车的各车轮、各钢轨磨损量相同。

2.2" 优化目标和决策变量

由第1节分析可知，纵断面方案由K个坡道的坡度i（k）和长度l（k）（k=1，2，…，K）确定，列车操纵方案由位置s处的牵引力F1（s）、F2（s）和制动力B1（s）、B2（s）确定（下标1、2分别代表上行方向和下行方向），以上要素为决策变量。

通过优化纵断面方案和列车操纵方案，一定研究时段内的最小化运营成本Cmin，见公式（1）：

Cmin=CE+CS+CW+CA，（1）

式中，CE、CS、CW和CA分别为给定研究时段内产生的能耗成本、闸瓦维修成本、车轮维修成本和钢轨维修成本。

2.2.1" 能耗成本计算

能耗成本为列车运行产生的牵引能耗相应的用电费用，若已知单位电价为cJ，能耗成本的计算公式为：

CE=cJEP，（2）

式中，E为列车双向牵引能耗；P为给定研究时间内列车在线路上往返运行的次数。根据牵引能耗定义，E的计算公式见公式（3）：

E=∑Rr=1E（r）1+∑Rr=1E（r）2，（3）

式中，R为划分的阶段数量；E（r）1和E（r）2分别为上行、下行方向第r阶段的牵引能耗，二者计算方法类似，以上行方向为例，E（r）1的计算方法见公式（4）：

E（r）1=∫s（r）fs（r）0F1（s（r））ds，（4）

式中，s（r）0和s（r）f分别为第r阶段起点和终点位置。

2.2.2" 闸瓦维修成本计算

当闸瓦厚度减少至一定限度，需更换闸瓦，由此产生的成本为闸瓦维修成本。已知在研究时段内，列车在线路上往返运行P次，所需闸瓦维修成本见公式（5）：

CS=「PUScSNS，（5）

式中，「表示向上取整数，cS、NS分别为单块闸瓦价格、列车闸瓦数量；US为闸瓦厚度减少到限时，列车在线路上往返运行的最大次数，其计算公式为：

US=ImS（IS1+IS2），（6）

式中，ImS为闸瓦最大磨损量；IS1和IS2为列车在上行、下行方向运行过程中闸瓦厚度减少量，由于二者计算方法类似，以IS1为例说明具体计算方法。在列车制动过程中，闸瓦与车轮接触使动能转换为热能，列车速度下降，同时闸瓦温度升高使闸瓦变薄，发生磨损，根据能量转换原理，IS1的计算见公式（7）：

IS1=∑Rr=1∫t1（s（r）f）t1（s（r）0）βγεMIa1（t）v1（t）NISIdt，（7）

式中，β为0-1变量，当制动力大于0时为1，否则为0；γ、ε分别为动能转换为热能的比例［22］、闸瓦吸收热能的比例［13］；t1（s）为列车在位置s处的运行时刻；MI为车轴质量；a1（t）、v1（t）分别为加速度和速度；NI、SI分别为车辆闸瓦数量和每块闸瓦的面积。

2.2.3" 车轮维修成本计算

车轮磨损源于车轮和钢轨间的相对滑动［23］，表现为轮缘厚度减少，车轮型面变得不规则。当车轮型面变化到一定程度时，不利于列车安全运行［24］，通常采用镟轮方式恢复，但镟轮将导致车轮踏面直径减小且无法恢复，踏面直径减少到限时，需更换车轮。因此，可用踏面直径衡量车轮磨损程度，计算维修成本CW，见公式（8）：

CW=「PUWcWNW，（8）

式中，cW、NW分别为单个车轮的维修价格、列车车轮数量；UW为车轮踏面直径减少到限时，列车在线路上往返运行的次数，其计算公式为：

UW=ImW（IW1+IW2），（9）

式中，ImW为车轮踏面直径最大磨损量；IW1、IW2为列车在上行、下行方向运行过程中车轮踏面直径减少量，由于二者计算方式类似，以上行方向为例，IW1可由轮缘厚度减少量换算，见公式（10）：

IW1=∑Rr=1∫s（r）fs（r）0θIL1（s（r））ds，（10）

式中，θ为踏面直径减少量与轮缘厚度减少量的比例，为一经验常数；IL1（s（r））为列车在上行方向运行过程中轮缘厚度减少量。由于车轮与钢轨接触作用过程复杂，且轮缘厚度减少量受线路、列车、轨道相关的诸多参数影响［23］，难以用数值方法计算。为此，采用仿真模型与数值方法相结合的方式，先基于仿真软件建立列车-轨道模型，获得轮轨间相互作用关系，再使用车轮磨耗模型计算轮缘厚度减少量，具体过程将在第3节介绍。

2.2.4" 钢轨维修成本计算

轮轨间相对滑动也将导致钢轨磨损，主要表现为波磨和侧磨两种形式［25］。其中，波磨产生原因复杂、难以预测，实际中采用定期打磨方式进行维护，本文研究的钢轨磨损为钢轨侧磨。侧磨主要发生在线路曲线上，按照《钢轨允许磨耗限度》［26］，以磨损深度为侧磨限度的衡量指标。当钢轨磨损深度到限时，对钢轨进行维修产生的成本为钢轨维修成本CA，计算方法见公式（11）：

CA=「PUAcANA，（11）

式中，cA、NA分别为单条钢轨的维修价格、钢轨数量；UA为钢轨磨损深度到限时，列车在线路上往返运行的次数，其计算公式为：

UA=ImA∑Rr1=1∫s（r）fs（r）0IA1（s（r））ds+∑Rr2=1∫s（r）fs（r）0IA2（s（r））ds，（12）

式中，ImA为钢轨磨损深度最大值；IA1（s（r））、IA2（s（r））为列车在上行、下行方向运行过程中第r阶段的钢轨磨损深度，与轮缘厚度减少量类似，钢轨磨损深度也需采用仿真模型与数值方法相结合的方式计算。

2.3" 约束条件

协同优化问题需同时考虑纵断面设计和定时列车控制两类约束。由于列车在上行和下行方向上运行时所受约束相似，以上行方向为例对模型约束进行介绍。

2.3.1" 纵断面设计约束

根据线路设计规范和工程建设要求，纵断面设计主要受车站及站外区域坡长、坡度约束，夹直线长度约束，车站高程约束，覆土厚度约束和避让区域约束的限制。

（1）车站及站外区域坡长、坡度约束

为保障列车运行平稳，避免跨坡道运行引起的列车振动，车站应尽量设置在一个坡道上，即车站区域进站和出站坡长之和大于站台长度，同时进站和出站坡度均采用满足排水要求的最小坡度id。假设车站进站和出站坡长相等，则车站区域坡长、坡度约束为：

l（k）≥Ls/2，（k=1，K），（13）

i（k）=id，（k=1，K），（14）

式中，Ls为站台长度。

站外区域坡长约束与车站区域类似，坡长应大于列车长度Lt，而坡度不仅要满足排水要求，还不能大于规定值im，确保列车运行安全，见公式（15～16）：

l（k）≥Lt，（k=2，3，…，（K－1）），（15）

id≤i（k）≤im，（k=2，3，…，（K－1））。（16）

（2）夹直线长度约束

根据地铁设计规范要求，相邻竖曲线间需使用不小于规定长度Lm的直线连接，确保线路平顺，有利于列车安全运行。连接相邻竖曲线的直线段为夹直线，如图3所示，夹直线长度约束可以表示为公式（17）：

l（k）－L（k－1，k）－L（k，k+1）≥Lm，（17）

式中，L（k-1，k）为第k-1个坡道与第k个坡道间竖曲线的切线长度，其计算公式为：

L（k－1，k）=Rki（k－1）－i（k）2 000，（18）

式中，Rk为第k-1个与第k个坡道间竖曲线的半径。

结合以上两个公式，可以将夹直线长度约束式（17）表示为公式（19）：

i（k－1）－i（k）+i（k）－i（k+1）≤2 000（l（k）－Lm）Rk。（19）

（3）覆土厚度约束

对于地下线，线路上方应保留厚度至少为G的覆土，避免地铁线路影响地面设施，该约束称为覆土厚度约束，见公式（20）：

H（s（r））lt;Hg（s（r））－G，（20）

式中，H（s（r））、Hg（s（r））分别为位置s（r）处的线路高程、地面高程，地面高程为已知条件。线路高程计算公式为：

H（s（r））=∑r－1m=1i（m）（s（m）f－s（m）0）+i（r）（s（r）－s（r）0）。（21）

（4）车站高程约束

由第1节的分析可知，在协同优化问题中，车站高程固定，可表示为公式（22）：

H（s（1）0）=H0，H（s（R）f）=Hf，（22）

式中，H0和Hf为起点和终点车站的高程。

（5）避让区域约束

避让区域为地下设施和不良水文地质所在区域，在设计纵断面时应绕行，该约束称为避让区域约束。对于在第p阶段的避让区域，用Q（p）表示避让区域所有的点，则约束可表示为公式（23）：

H（s（p））－Hq（s（p））gt;0，（q∈Q（p）），（23）

式中，Hq（s（p））为第p阶段避让区域中q点的高程。

2.3.2" 定时列车控制约束

（1）定时运行约束

定时列车控制为在给定区间运行时分下，采用适当的牵引力和制动力，使列车耗费最少的牵引能耗从区间起点运行至终点。因此，列车在起点和终点的位置、运行时分、速度均为固定值，该约束称为定时运行约束，见公式（24～26）：

s1（s（1）0）=S0，s1（s（R）f）=Sf，（24）

t1（s（1）0）=0，t1（s（R）f）=T，（25）

v1（s（1）0）=v1（s（R）f）=0，（26）

式中，S0和Sf分别为起点、终点水平位置；T为给定的区间运行时间，计算方法见公式（27）：

T=3.6（Sf－S0）vc，（27）

式中，vc为技术速度。

（2）区间速度约束

为确保行车安全，列车在区间运行过程中不得超速运行，应与限定速度保持一定差距Δv，即区间速度约束为：

0lt;v1（s（r））≤vm（s（r））－Δv，（28）

式中，vm（s（r））为在s（r）处的限定速度。

（3）牵引力和制动力约束

根据列车牵引制动特性，在同一时刻，列车最多只能使用牵引力或制动力中的一种，且所用牵引力或制动力不能超过限定值，可表示为公式（29～30）：

0≤F1（s（r））≤Fm（s（r）），0≤B1（s（r））≤Bm（s（r）），（29）

F1（s（r））B1（s（r））=0，（30）

式中，Fm（s（r））、Bm（s（r））为最大牵引力、最大制动力。

为精确计算使用的牵引力、制动力，需结合列车受力分析、牛顿第二定律等，建立列车运动方程，描述列车运行行为。列车运动方程可表示为：

dv1（s（r））ds=F1（s（r））－B1（s（r））－W1（s（r））－N1（s（r））M（1+ρ）v1（s（r）），（31）

dt1（s（r））ds=1v1（s（r）），（32）

式中，W1（s（r））、N1（s（r））分别为列车运行过程中所受的基本阻力和附加阻力，附加阻力包括坡道附加阻力和曲线附加阻力；M为列车质量；ρ为回转质量系数，为与列车类型有关的常数；v1（s（r））、t1（s（r））分别为列车速度和运行时间。基本阻力、附加阻力的计算方法为：

W1（s（r））=Mga+bv1（s（r））+cv1（s（r））2，（33）

N1（s（r））=Mgi（s（r））+600L（s（r））R（s（r））Lt，（34）

式中，g为重力加速度；a、b、c为与列车性质有关的常量；i（s（r））为坡度；R（s（r））为线路曲线半径；L（s（r））为列车在曲线上的长度；Lt为列车长度。

（4）阶段连接约束

由于模型将区间划分为多个阶段，为得到连续的列车操纵方案，需对相邻阶段交汇点的速度、时间、位置进行约束，以获得完整的列车操纵方案，该约束称为阶段连接约束。阶段连接约束为第r阶段终点和第r+1阶段起点的速度、时间、位置相等，见公式（35～37）：

s（r）f=s（r+1）0，（1≤r≤R－1），（35）

v1（s（r）f）=v1（s（r+1）0），（1≤r≤R－1），（36）

t1（s（r）f）=t1（s（r+1）0），（1≤r≤R－1）。（37）

3" 算法设计

以上多阶段优化模型具有非线性性强、变量和约束多等特点，求解难度大。列车控制优化研究对比了伪谱法、动态规划和混合整数规划算法的求解精度和效率，结果表明伪谱法具有更高的求解精度、更快的求解速度，同时变量和约束的数量对伪谱法求解速度影响很小，适用求解多阶段优化模型［27］。因此，本文采用伪谱法求解多阶段优化模型，其中阶段划分由蛮力搜索算法（BF算法）完成，车轮、钢轨维修成本基于列车-轨道动力学仿真计算。

3.1" 算法框架

本文算法基于列车-轨道动力学仿真、综合伪谱法和BF算法。列车-轨道动力学仿真的作用为计算不同线路条件和列车速度下的车轮、钢轨磨损量，形成轮轨磨耗数据库，该过程将于第3.2节详细说明。BF算法用于搜寻符合约束条件的坡长方案，并依据第2节的分阶段原则将区间划分为多个阶段。伪谱法则基于轮轨磨耗数据库和阶段划分方案，求解最小化双向能耗成本和维修成本之和的协同优化方案。

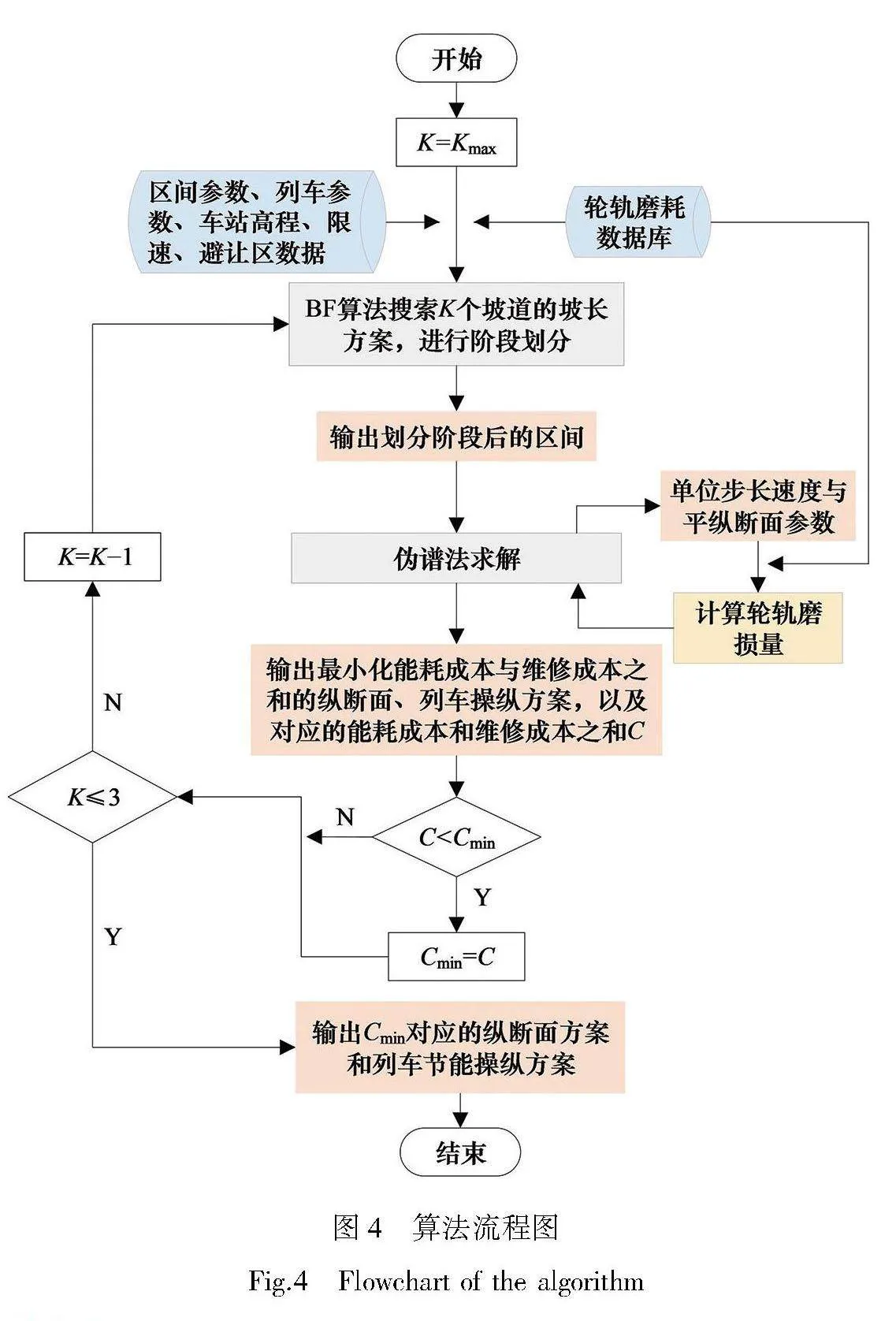
若已有轮轨磨耗数据库，算法流程如图4所示。具体步骤为：

步骤1：参数初始化。输入区间线路平面参数、车站高程、列车参数、线路限速、避让区域位置、轮轨磨耗数据库等，计算区间最大坡道数量Kmax，令K=Kmax：

Kmax=（L－Ls）/Lt」。（38）

步骤2：阶段划分。运用BF算法搜索满足式（18）和式（20）的全部K个坡道组合方案，在此基础上根据第2节的阶段划分原则将区间划分为R个阶段。

步骤3：伪谱法求解。基于阶段划分方案和轮轨磨耗数据库，采用伪谱法求解K个坡道的最优坡度和定时列车控制方案，对比各优化方案成本，获得成本最小的K个坡道的最优纵断面方案和列车控制方案。伪谱法原理为将问题离散变换为非线性规划问题后求解，该过程基于MATLAB开发的GPOPS II完成，数学原理在Wang等［20］的文章中详细阐述。

步骤4：优化方案对比。将目前最优协同优化方案与步骤3输出的K个坡道的协同优化方案进行对比，令能耗成本和维修成本之和更小的方案为新的最优协同优化方案，至步骤5。

步骤5：循环判断。判断K≤3是否满足，若是，则结束算法，输出最优协同优化方案，否则令K=K-1，转至步骤2。

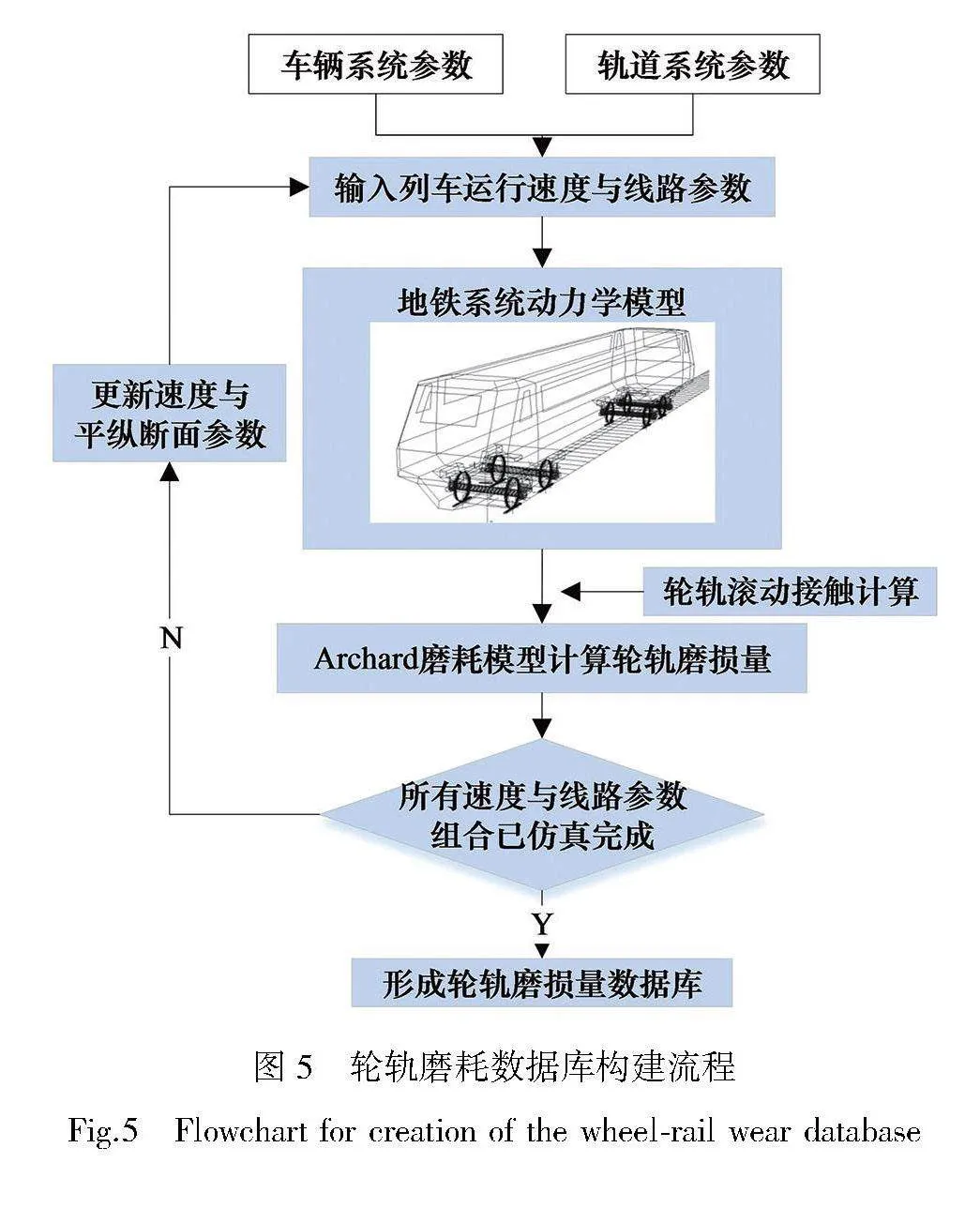
3.2" 轮轨磨耗数据库构建方法

列车行驶过程中，线路条件和速度都可能发生变化，导致不同位置处的轮轨磨耗程度不同。以上因素对轮轨磨损的共同影响难以用数学公式表达，无法使用数值方法计算不同优化方案下的轮轨磨损量。因此，本文构建轮轨磨耗数据库，在优化过程中调用数据库计算轮轨磨损量，估算轮轨维修成本。

根据第2节维修成本分析，轮轨磨耗数据库数据包括单位步长车轮踏面直径减少量、钢轨磨损深度减少量，数据基于SIMPACK软件仿真计算获得。构建数据库的流程如图5所示。

首先输入车辆和轨道系统固定参数、线路坡度和曲线半径以及列车速度，建立列车-轨道仿真模型，获得轮轨接触参数；接着用磨耗模型计算单位步长车轮轮缘厚度减少量及相应踏面直径减少量、钢轨磨损深度减少量；不断改变线路坡度、曲线半径和列车速度的组合，重复以上步骤，直至完成对所有组合条件的仿真计算，形成轮轨磨耗数据库。

4" 案例分析

本文应用广州地铁3个区间进行案例分析，基于SIMPACK计算并比较不同速度、坡度下的车轮和钢轨磨损量差异，总结轮轨磨损规律，形成轮轨磨耗数据库。基于轮轨磨耗数据库，对比协同优化方案和基于实际纵断面的列车控制优化方案的成本大小，验证协同优化方法的优化效果。算法框架在MATLAB R2018b中编程实现，伪谱法求解过程基于GPOPS II完成。

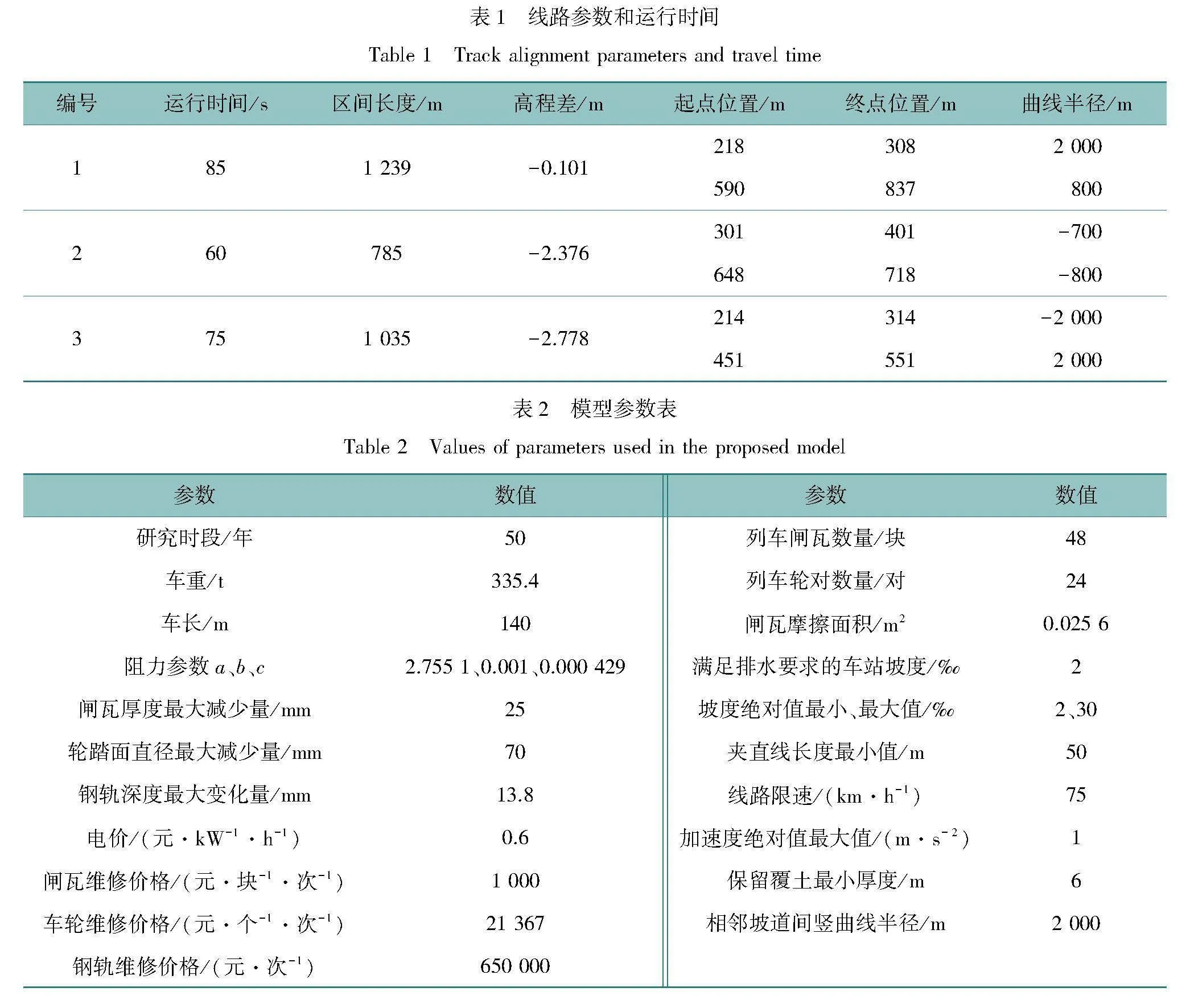
4.1" 基础数据

已知的线路参数和运行时间如表1所示，模型中主要参数的值见表2，纵断面设计约束相关参数根据《地铁设计规范》和实际情况取值。列车特性曲线如图6所示。构建列车-轨道动力学模型时，车轮外形为LM型，钢轨为UIC60钢轨。

4.2" 轮轨磨损变化规律

为计算单位步长车轮轮缘厚度减少量、钢轨磨损深度减少量，形成轮轨磨耗数据库，在仿真线路上建立列车-轨道动力学模型。仿真线路依次由直线、缓和曲线、圆曲线、缓和曲线和直线组成，直线、圆曲线长度均为100 m，缓和曲线长度按曲线半径取值。根据表2中的曲线半径，仿真线路圆曲线半径取值为700、800和2 000 m。根据《地铁设计规范》和限速，坡度取值范围为［-30‰，-2‰］和［2‰，30‰］，列车速度在10～75 km/h间取值。

根据仿真计算结果，当曲线半径、列车速度一定，分别为700 m和70 km/h时，车轮和钢轨磨损量随坡度变化情况如图7所示。由图7可知，无论是上坡或下坡，车轮和钢轨单位步长磨损量都随着坡度绝对值增大而增加。当其他条件相同时，相比列车在上坡道上运行，列车在下坡道上运行的轮轨磨损量一般更大。

选取坡度为-25‰的情形，对曲线半径分别为700和2 000 m，不同列车速度下的轮轨磨损量进行分析，磨损量变化如图8所示。当曲线半径不变时，车轮和钢轨单位步长磨损量随列车速度增加而增长。当列车速度一定时，曲线半径越大，车轮和钢轨单位步长磨损量越小。综合以上分析，如果不考虑能耗成本和约束条件等，曲线半径越大、列车速度和坡度绝对值越小，轮轨维修成本将越低。

4.3" 协同优化模型和列车控制优化模型效果对比

为论证协同优化方法的优化效果，基于轮轨磨耗数据库，对表1的3个区间使用本文模型和列车控制优化模型，对比同区间不同方案下的成本大小。列车控制优化模型的基础为Wang等［27］提出的模型，将约束条件与本文模型保持一致，该模型采用实际纵断面，仅对给定区间运行时分条件下的列车控制方案进行优化，使得能耗成本和维修成本之和最小。

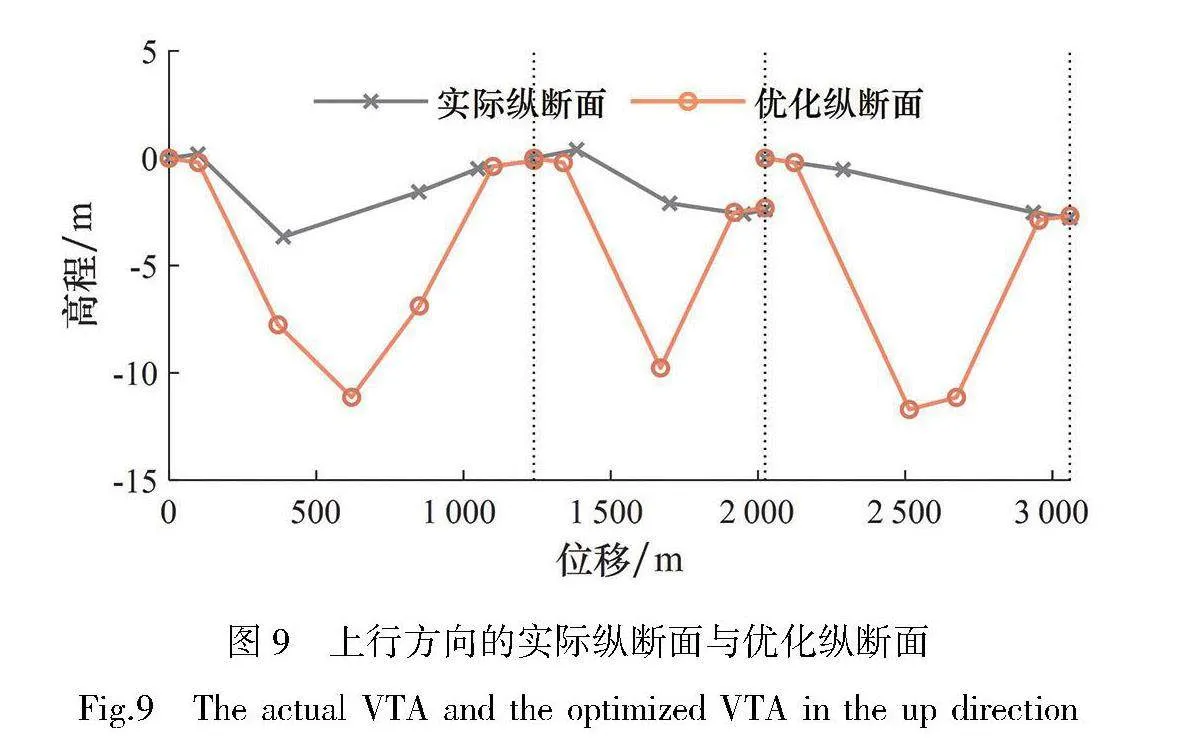
协同优化模型求解的纵断面方案和实际纵断面方案如图9所示，图中为上行方向纵断面方案，该方案轴对称即为下行方向纵断面方案。由于3个区间不是连续区间，起点高程都设为0 m。由图可知，相比3个区间的实际纵断面方案，优化纵断面方案的高程最小值更小，站外区域出站、进站坡度都更大。

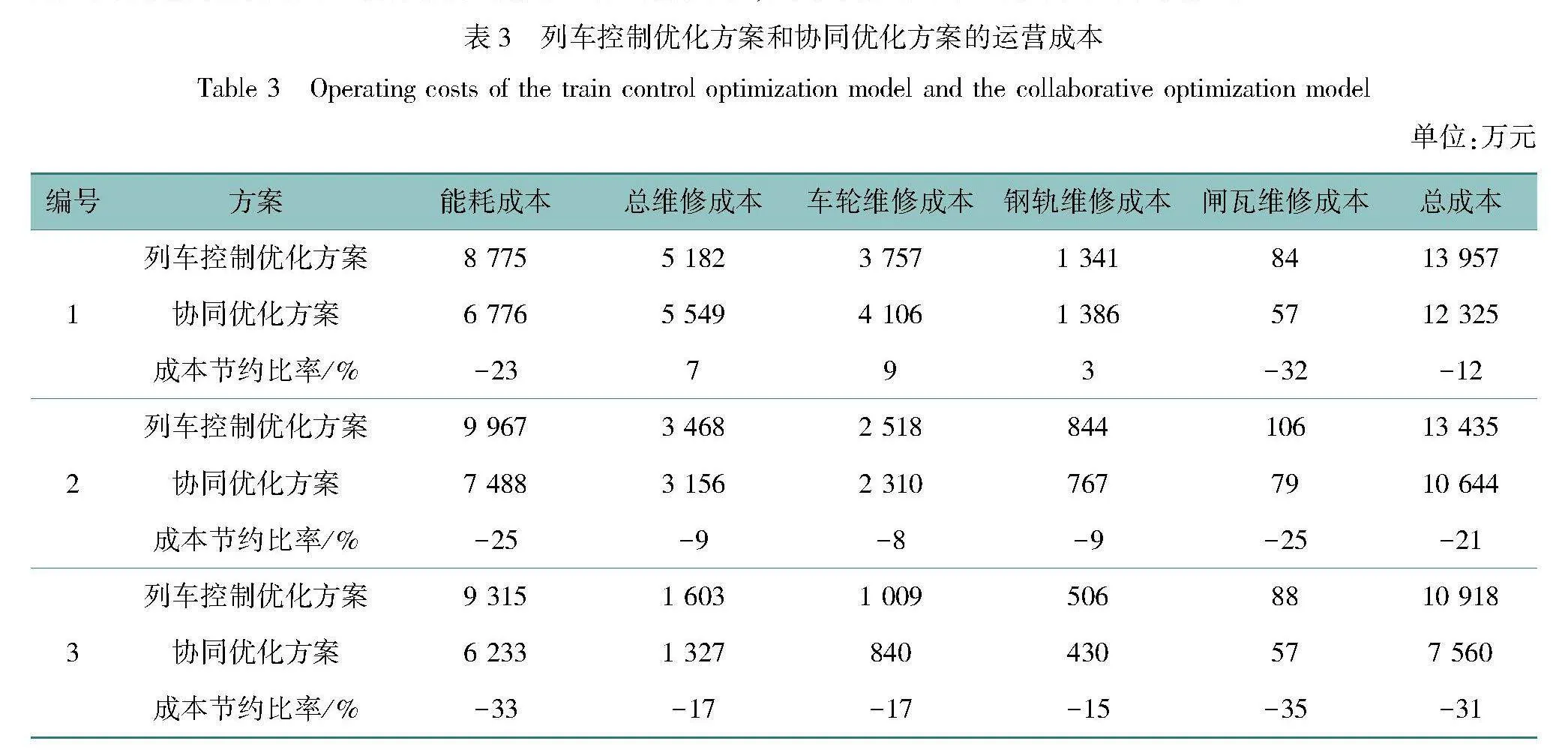
当列车在两种纵断面上运行，研究年度产生的成本如表3所示，成本节约比率为本文模型优化方案相比列车控制优化模型求解方案的成本变化情况。在各区间，本文模型优化方案较列车控制优化模型求解方案都具有更好的优化效果，能耗成本和维修成本之和都更小，平均降低了21%。因此，相比只优化定时列车控制方案，同时对纵断面和列车控制方案进行优化更有助于降低运营成本。

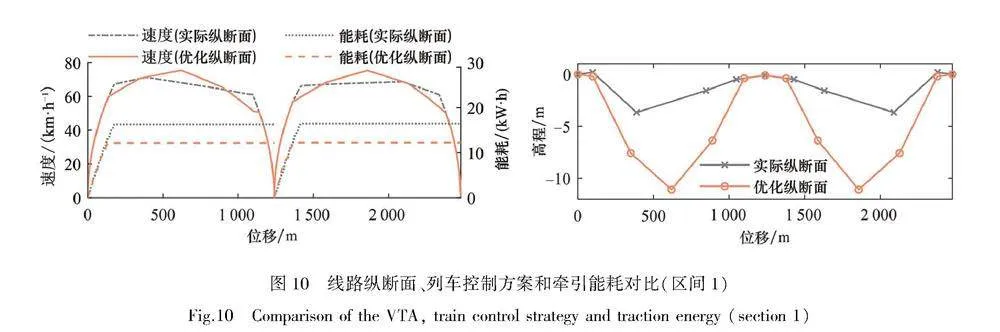
对于各区间的能耗成本，相比列车控制优化模型求解方案，本文模型优化方案都具有更好的优化效果，平均优化率为27%。为说明能耗成本节约的原因，以第一个区间的优化结果为例进行分析，如图10所示。

结合图中能耗变化和列车操纵方案，可知列车能耗增长仅发生在出站牵引阶段，随后列车采用不耗能的惰行工况运行，直至制动减速进站停车。在列车牵引阶段，由式（4），所需能耗取决于牵引力和牵引距离大小。列车在实际线路上运行时，牵引距离和牵引力都不小于优化方案，所以耗能更多。对比纵断面方案可知，优化方案站外区域的下坡坡度更大，当列车处于牵引工况时，利用重力势能转化为动能，可使用更小的牵引力获得与在实际纵断面上运行时相同的加速度。同时，当列车处于惰行工况时，在优化纵断面上能充分利用重力势能获得更大运行速度以满足运行时分要求，则牵引阶段的运行距离可以更短。

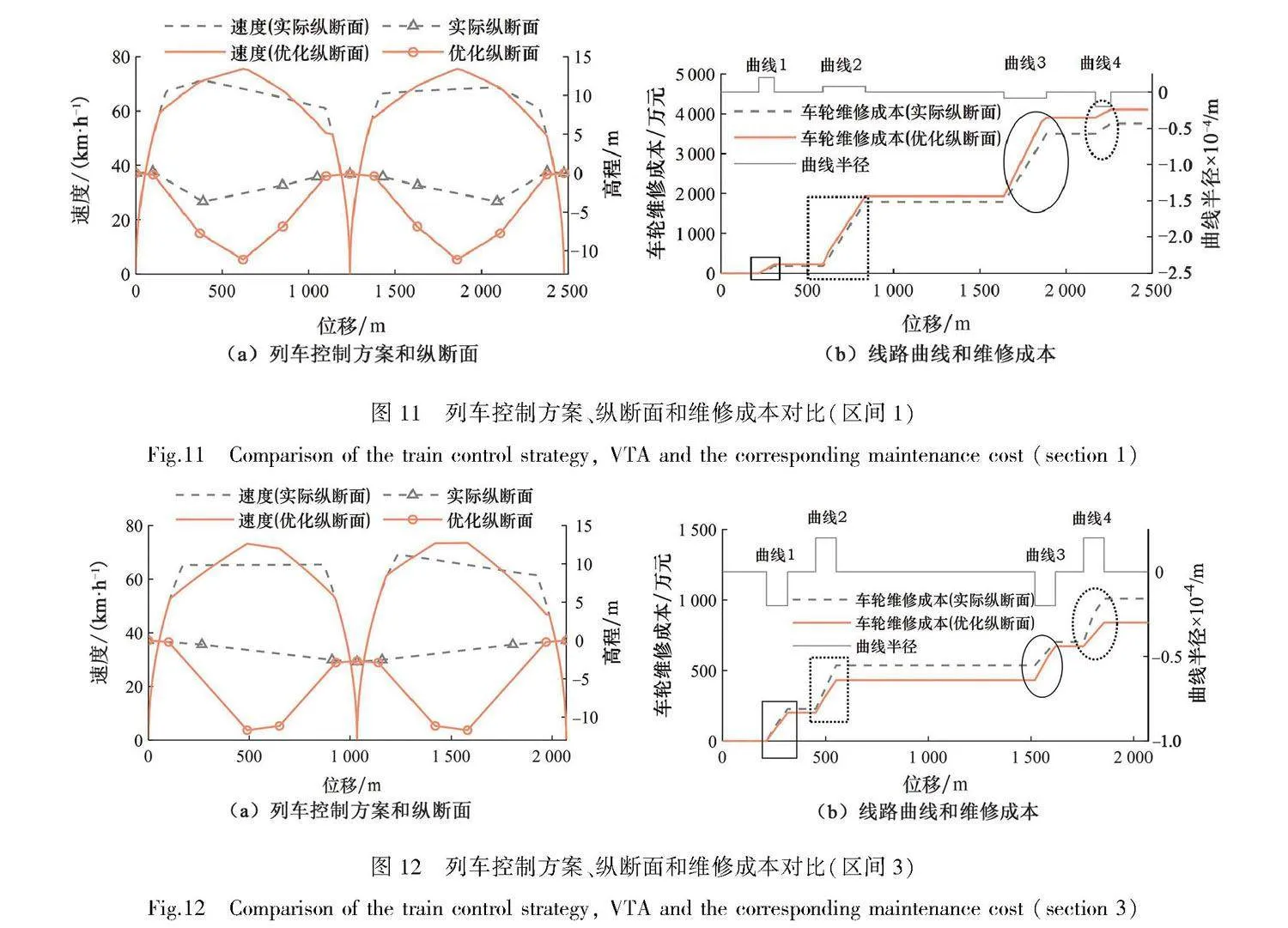
对于维修费用，在后两个区间上，优化方案的维修费用小于列车操纵优化模型求解方案的维修费用，但在第一个区间，优化方案的维修费用更高，主要由轮轨维修费用较大导致。由于轮轨磨损变化规律相似，结合轮轨磨损变化规律，对第一和第三个区间的车轮维修费用进行分析，如图11、12所示。

图11（a）为列车控制方案和纵断面对比，图11（b）为线路曲线和车轮维修成

本对比。由图11（b）可知，第一个区间双向共有4处曲线，从左至右依次记为

曲线1～4。在曲线1、4上，结合图11（a）可知，相比实际纵断面，优化纵断面坡度绝对值更大，但列车速度更小，两种纵断面上车轮磨损量接近。在曲线2、3上，结合图11（a）可

知，优化纵断面坡度绝对值和列车速度都大于实际纵断面，所以车轮磨损量更大。综合4个曲线上的车轮磨损量，最终优化纵断面上车轮磨损量大于实际纵断面上车轮磨损量，相应维修成本也更大。

图12（a）为列车控制方案和纵断面对比，图12（b）为线路曲线和车轮维修成本对

比。由图12（b）可知，第3个区间双向共有4处曲线，从左至右依次记为曲线

5～8。在曲线5、8上，结合图12（a）可知，相比实际纵断面，虽然优化纵断面坡度更大，但列车速度更小，导致车轮磨损量稍小。在曲线6上，结合图12（a）可知，虽然优化纵断面上的列车速度更大，但所处位置为上坡，而实际纵断面相应位置为下坡，由于下坡时车轮磨损量一般更大，此时列车在优化纵断面上的车轮磨损量更小。在曲线7上，结合图12（a）可知，相比实际纵断面，优化纵断面为下坡且列车速度更大，所以车轮磨损量更大。综合4个曲线上的车轮磨损量，最终优化纵断面上车轮磨损量小于实际纵断面上车轮磨损量，相应维修成本也更小。结合第1和第3个区间的维修成本分析可知，在其他条件相同时，车轮维修成本受坡度、列车速度共同影响，车轮磨损量及相应维修成本需结合具体场景进行分析。

5" 结语

相比仅优化列车控制，在设计纵断面时优化列车控制将有助于节约运营成本。本文以最小化能耗成本和维修成本之和为目标，提出了考虑定时列车控制对纵断面进行优化的模型，并基于列车-轨道动力学仿真，设计了综合伪谱法和蛮力搜索的算法求解。通过广州地铁三个区间的实例证明，对比仅优化定时列车控制方案，本文模型优化方案对降低能耗成本和维修成本具有更好的优化效果，各区间平均优化率为21%。本文所用伪谱法采用通用求解器实现，考虑协同优化问题求解时间较长，未来可结合问题特点开发专用求解器，提高求解效率。

参考文献：

［1］中国城市轨道交通协会. 城市轨道交通2022年度统计和分析报告［EB/OL］. ［2024-04-01］.https：//www.camet.org.cn/xytj/tjxx/11944.shtml.

［2］GONZLEZ-GIL A， PALACIN R， BATTY P， et al. A systems approach to reduce urban rail energy consumption［J］. Energy Conversion and Management， 2014， 80： 509-524. DOI： 10.1016/j.enconman.2014.01.060.

［3］DOUGLAS H， ROBERTS C， HILLMANSEN S， et al. An assessment of available measures to reduce traction energy use in railway networks［J］. Energy Conversion and Management， 2015， 106： 1149-1165. DOI： 10.1016/j.enconman.2015.10.053.

［4］HOANG H， POLIS M， HAURIE A. Reducing energy consumption through trajectory optimization for a metro network［J］. IEEE Transactions on Automatic Control， 1975， 20（5）： 590-595. DOI： 10.1109/tac.1975.1101058.

［5］JHA M K， SCHONFELD P， SAMANTA S. Optimizing rail transit routes with genetic algorithms and geographic information system［J］. Journal of Urban Planning and Development， 2007， 133（3）： 161-171. DOI： 10.1061/（asce）0733-9488（2007）133： 3（161）.

［6］KIM M E， SCHONFELD P， KIM E. Simulation-based rail transit optimization model［J］. Transportation Research Record： Journal of the Transportation Research Board， 2013， 2374（1）： 143-153. DOI： 10.3141/2374-17.

［7］柏赟， 白骁， 孙元广， 等. 地铁线路区间纵断面节能设计优化模型［J］. 铁道学报， 2020， 42（9）： 10-16. DOI： 10.3969/j.issn.1001-8360.2020.09.002.

［8］彭磊， 樊葱， 汪茜， 等. 地铁线路纵断面优化系统设计与实现［J］. 山东科学， 2022， 35（4）： 136-143. DOI： 10.3976/j.issn.1002-4026.2022.04.017.

［9］徐杨. 考虑建设成本和运营能耗的地铁线路纵断面设计优化［D］. 北京： 北京交通大学， 2020： 27-54.

［10］WU C X， LU S F， XUE F， et al. Earth potential as the energy storage in rail transit system-on a vertical alignment optimization problem［C］//2018 21st International Conference on Intelligent Transportation Systems （ITSC）. Maui， HI. IEEE， 2018： 2729-2734 DOI： 10.1109/itsc.2018.8569925.

［11］DUARTE M A， SOTOMAYOR P X. Minimum energy trajectories for subway systems［J］. Optimal Control Applications and Methods， 1999， 20（6）： 283-296. DOI： 10.1002/（sici）1099-1514（199911/12）20： 6lt;283： aid-oca661gt;3.0.co;2-k.

［12］汤超. 平纵断面线型及轨道类型对地铁轨道动力特性和钢轨磨耗影响研究［D］. 北京： 北京交通大学， 2012： 31-64.

［13］肖绯雄， 陈旭. 恶劣工况下货车高摩合成闸瓦磨损分析［J］. 北京交通大学学报， 2014， 38（4）： 20-25. DOI： 10.11860/j.issn.1673-0291-2014.04.004.

［14］LAI X R， SCHONFELD P. Optimization of rail transit alignments considering vehicle dynamics［J］. Transportation Research Record： Journal of the Transportation Research Board， 2012， 2275（1）： 77-87. DOI： 10.3141/2275-09.

［15］KANG M W， JHA M K， BUDDHARAJU R. Rail transit route optimization model for rail infrastructure planning and design： Case study of saint Andrews， Scotland［J］. Journal of Transportation Engineering， 2014， 140（1）： 1-11. DOI： 10.1061/（asce）te.1943-5436.0000445.

［16］中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.GB 50157—2013地铁设计规范［S］. 北京：中国建筑工业出版社，2014.

［17］岳小丽， 刘柳林. 隧道盾构法施工的成本分析和降低措施［J］. 工业建筑， 2009， 39（S1）： 755-758.

［18］廖涛. 动车组制动闸片寿命预测关键技术的研究与实现［D］. 北京： 北京交通大学， 2015： 9-15.

［19］耿传智， 余庆. 地铁轨道结构减振性能的仿真分析［J］. 同济大学学报（自然科学版）， 2011， 39（1）： 85-89. DOI： 10.3969/j.issn.0253-374x.2011.01.016.

［20］WANG P L， GOVERDE R M P. Multiple-phase train trajectory optimization with signalling and operational constraints［J］. Transportation Research Part C： Emerging Technologies， 2016， 69： 255-275. DOI： 10.1016/j.trc.2016.06.008.

［21］王平， 郭强， 李晨钟， 等. 蠕滑曲线对地铁小半径曲线轮轨接触特性的影响［J］. 中南大学学报（自然科学版）， 2020， 51（4）： 1145-1153. DOI： 10.11817/j.issn.1672-7207.2020.04.029.

［22］陈旭. 货车闸瓦不同工况仿真分析及磨损研究［D］. 成都： 西南交通大学， 2015： 18-20.

［23］杨绪杰. 基于几何与动力学参数的山区线路地铁车辆轮轨磨耗控制研究［D］. 重庆： 重庆交通大学， 2014： 1-14.

［24］于春广， 陶功权. 地铁车轮磨耗测试及数值仿真［J］. 工程力学， 2016， 33（1）： 201-208. DOI： 10.6052/j.issn.1000-4750.2014.06.0484.

［25］沈建文， 高亮， 戴春阳， 等. 减振轨道形式对地铁曲线上钢轨磨耗影响的仿真［J］. 北京交通大学学报， 2011， 35（4）： 38-43. DOI： 10.3969/j.issn.1673-0291.2011.04.008.

［26］中华人民共和国铁道部.TB 2097—1989钢轨允许磨耗限度［S］. 北京：中华人民共和国铁道部，1990.

［27］WANG Y H， DE SCHUTTER B， VAN DEN BOOM T J J， et al. Optimal trajectory planning for trains：a pseudospectral method and a mixed integer linear programming approach［J］. Transportation Research Part C： Emerging Technologies， 2013， 29： 97-114. DOI： 10.1016/j.trc.2013.01.007.