基于车体加速度的超大跨度桥上线路纵断面优化方法

2024-04-12舒英杰王铭陆粤禹壮壮陈嵘王平

铁道标准设计 2024年4期

舒英杰，王铭，陆粤，禹壮壮，陈嵘，王平

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031;3.西南交通大学桥梁工程系,成都 610031)

引言

随着我国交通强国战略的实施和高速铁路建造技术的发展,超大跨度桥梁被应用于环境复杂艰险地区,成为跨海、跨谷的交通要道[1]。受钢梁制造误差、施工偏差等因素影响,超大跨度桥梁成桥线形往往与设计线形存在偏差,在温度、风等环境荷载作用下还会产生较大的动态挠曲变形[2-4],导致轨面实际高程与设计高程存在偏差,铺轨后的线路调整能力难以实现设计纵断面。为此,在线路开通前,需结合调整能力重新设计能够适应既有成桥线形的线路纵断面,并通过调坡的方式实现线路纵断面调整[5-6]。由于桥上线路受桥梁成桥线形影响,工程实践中变更后的纵断面可能不满足线路设计规范或行车要求,进而严重影响桥梁的正常验收及列车的达速运营,桥上线路纵断面设计及优化方法亟待创新。

现有线路纵断面优化研究主要以一般区间线路为对象,如李伟等[7]基于“点线一致”思想,提出一种既有铁路纵断面的自动重构方法,能够自动生成满足约束的纵断面优化方案,显著减少测点到重构线路的调整量;OBRIEN等[8]依据车体转向架垂向加速度及角速度,提出基于交叉熵优化技术的线路纵断面识别及优化方法;PU等[9]提出一种自动全局迭代方法,能够自动识别既有线路纵断面的竖曲线等线路要素,可用以指导纵断面重整。目前桥上线路研究较少,设计及评估几乎完全依赖于桥梁的挠曲线形,一般依据桥梁结构简单采用“人字坡+圆曲线过渡”“平坡+预拱度”的方式设计线路[10-12];采用样条插值或最小二乘法对桥梁挠曲线形进行拟合,从而得到线路平纵断面,依据车体响应或线路参数判断线路是否满足规范要求[13-14],其实质上是使线路尽量“贴合”桥梁,若用于线路优化,则未考虑桥梁的成桥线形偏差及线路调整条件,实际运用存在困难。

超大跨度铁路桥上线路不同于普通区间线路,一方面桥梁成桥线形存在偏差导致线路设计纵断面难以实现,另一方面桥梁受温度荷载作用动态变形明显,导致桥上线路纵断面不易保持,使得基于普通区间线路制定的线路设计指标已无法指导大跨度铁路桥梁的动态线路设计[12]。基于此,开展桥上线路纵断面优化方法研究,以实测成桥线形为设计基准,充分考虑道床的可调整厚度及线路的平顺衔接,结合傅里叶级数原理建立目标优化模型,提出一种基于车体加速度的桥上线路纵断面级数曲线优化方法,对大跨桥上线路纵断面设计及优化有重要意义。

1 工程背景

某超大跨度悬索桥为五跨双塔连续钢桁梁悬索桥,主桥桥跨布置为(84+84+1 092+84+84)m,立面布置如图1所示。该桥为公铁两用桥,上层通行双向八车道高速公路,设计行车速度100 km/h;下层通行四线铁路,其中双线客运专线设计速度250 km/h,预留双线铁路设计速度200 km/h。桥梁设计纵断面位于坡度3‰、坡长1 214 m和坡度-3‰、坡长928 m“人”字坡上。

图1 超大跨度悬索桥立面布置(单位:m)Fig.1 Elevation layout of super long-span suspension bridge (unit: m)

大桥轨道初步铺设完成后,在气温较为稳定时(12 ℃),实测沿线路方向主桥面成桥线形,通过理论计算的温度变形换算至设计基准温度(15 ℃)后,其与设计高程的对比如图2所示。该桥边跨段与设计线形吻合较好,主跨段实测高程高于设计高程,偏差呈现“中间大、两边小”的趋势。主跨跨中高于原设计高程43.3 cm,偏差最大高于原设计高程51 cm。

由于桥上线路纵断面依附于桥梁结构,实测桥梁高程与设计高程的偏差为线路纵断面设计调整带来了困难。在保证道床具有合理厚度的前提下,根据TB 10098—2017《铁路线路设计规范》[15]理论公式

(1)

计算最小坡段长度后,对实测桥梁线形进行拟合,线路纵断面需近似拟合为6个坡段,如图3所示。多坡段形式纵断面一方面引入多个变坡点,对行车舒适性不利;另一方面,拟合的线路纵断面呈现坡度3‰微幅波动的短坡段,坡段长度不满足TB 10098—2017《铁路线路设计规范》困难条件下最小坡段长度不应小于600 m,且不应连续使用的规定[15]。上述因素直接影响了大桥的成桥验收以及后期线路的运营维护,迫切需要一种新方法设计纵断面,使其与既有桥梁线形及线路调整条件契合,并满足行车要求。

图3 多坡段纵断面示意(里程:m;坡度:‰)Fig.3 Schematic diagram of the multi-slope line profile (mileage:m; gradient:‰)

2 桥上线路纵断面优化方法

线路纵断面的合理性主要取决于行车性能,其与线路的波长特性密切相关[16-17],因此,可在纵断面设计时考虑波长成分,从根本上实现线路设计与行车性能的关联关系。若能将不同波长线形以某种方式组合形成纵断面,即可实现上述目的,傅里叶级数不失为一简单途径。

2.1 线路纵断面的傅里叶级数形式

傅里叶级数可使任何周期函数以三角函数的形式展开,可设优化后的纵断面为函数R(x),在空间域上可表示为

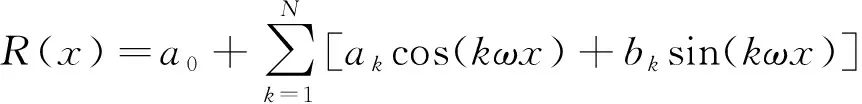
(2)

式中,R(x)为线路纵断面的轨面高程;x为线路里程组成的向量x={x1,x2,…,xi,…,xn};a0为偏移量;ak、bk为第k阶傅里叶系数,即余弦与正弦波形的幅值;kω为第k阶傅里叶级数的频率,即波长为2π/kω;N为傅里叶级数的阶数,根据需要选取。

由于傅里叶级数本身的特点,将线路纵断面设定为傅里叶级数的形式可带来以下优势:简单的函数形式可方便地计算每一里程处的高程,有利于现场精调及后期维护;由于傅里叶级数为连续函数,一阶导数、二阶导数连续,因此线形圆顺,可较为容易地满足轨道平顺性及行车要求;由于满足条件的纵断面均可表示为傅里叶级数的形式,因此可用于成桥线形偏差的评估,即若能优化出满足要求的线路纵断面,则可从线路角度认为桥梁施工偏差满足要求;此外,傅里叶级数直观反映了线路纵断面的频域特征——波长和幅值,为纵断面设计以及列车响应评估带来新思路。

2.2 基于车体加速度的纵断面目标优化模型

传统线路纵断面为直坡段与竖曲线的组合,主要包括最大坡度、最小曲线半径、最小坡段长度等设计参数,设计人员根据设计参数,凭借经验设计出相对较优的方案[18]。若将线路纵断面设计问题转化为目标优化问题,在考虑相关约束条件后,使用优化算法自动搜索出最优的线路方案,可避免有价值方案的遗漏,并提高设计效率[19]。

不同于普通区间线路,桥上线路依附于桥梁结构,纵断面设计需以桥梁线形为基准,侧重考虑行车性能以及线路衔接。大跨度桥梁在温度、风等荷载作用下会产生较大挠曲变形,桥上线路较普通区间线路引入了长波成分[20],因此列车通过大跨度桥梁时的加速度响应包括离心加速度与振动加速度。车体离心加速度仅与曲线半径及车速有关,可将最大离心加速度作为纵断面的优化目标,同时也间接控制了线形的曲线半径。

车体振动加速度与线路中的波长成分密切相关,其中某些波长成分会引起较大的振动加速度,称之为敏感波长[16]。可通过调整式(2)函数阶数N使线路中的波长成分大于敏感波长Ls,从而控制振动加速度。优化纵断面中最大波长为线路长度xn-x1,最小波长由傅里叶级数的阶数决定,其值为(xn-x1)/N。因此,通过选择傅里叶级数阶数,即N<(xn-x1)/Ls时,车体振动加速度可得到控制,模型可不考虑其影响。

桥上线路还需考虑与路、隧段线路的衔接,因此需将线路纵断面端部坡度作为约束条件;此外,道床厚度对轨道结构以及桥梁结构变形的影响也不容忽视[21],需将道床厚度作为约束条件。目标优化模型如式(3)所示。

T1≤R(xi)-B(xi)≤T2∀xi∈x

(3)

式中,sp1、sp2、sp3、sp4分别为线路纵断面端部坡度的容许值;T1、T2分别为道床厚度的下限和上限;B(xi)为里程xi处的实测桥梁高程;ALX(xi)为里程xi处的离心加速度,其计算式为

(4)

其中,线路等效半径Si可由下式得到

(5)

由于采用傅里叶级数的形式,线形平顺,未人为加入变坡点,目标优化模型中不考虑最小坡段长度及坡度代数差;目前大跨度铁路桥梁纵断面均采用“人字坡+圆曲线过渡”或“平坡+预拱度”的方式[11],作为拟合基准的桥梁线形即可满足列车的通行能力,因此目标优化模型中暂不考虑最大坡度的影响。

需注意的是,当阶数越小时,虽然线路纵断面中最小波长越远离敏感波长、波长成分更为简单,但是,纵断面线形却更脱离桥梁线形,故阶数应有一下限,其与约束条件有关,可通过提前试算得到。因此,傅里叶级数阶数上限取决于车体敏感波长及桥梁长度,用以减小车体振动加速度;阶数下限取决于约束条件,与桥梁线形状态相关。通过阶数,将线路纵断面设计与行车性能、桥梁线形状态进行了关联。

由于传统优化算法一般需要函数的导数信息,或者依赖初始点的选择,效率较低,而遗传算法作为启发式算法可避免以上缺陷。故本文采用遗传算法对优化模型进行求解。

3 桥上线路纵断面优化实例

依据超大跨度悬索桥的实测桥梁线形,使用前述优化模型对纵断面进行重新设计,分析其优化效果,进一步验证模型的适应性与合理性。为不失一般性,根据工程实践经验,设定优化后的线路纵断面端部坡度范围为0～3‰,道床厚度为330～450 mm[2]。

3.1 基于敏感波长的阶数选取

在软件SIMPACK中建立车辆-轨道耦合动力学模型[22],车辆参数取自CRH3型动车组。通过反演德国低干扰轨道谱,得到30条波长0.5～300 m的随机不平顺,将其作为线路激励输入模型,进而计算得到不同速度下车体垂向加速度的功率谱密度。为便于分析,将结果进行了最大值归一化处理,如图4所示。

图4 归一化车体垂向加速度功率谱密度Fig.4 Normalized PSD of vehicle vertical acceleration

由图4可知,200 km/h时车体敏感波长范围大致为40～120 m,最敏感波长为58 m;250 km/h时车体敏感波长范围大致为50～150 m,最敏感波长为80 m;300 km/h时车体敏感波长范围大致为60～170 m,最敏感波长为91 m;350 km/h时车体敏感波长范围大致为70～200 m,最敏感波长为117 m。由此可保守认为车体加速度最大敏感波长为200 m。

由于线路纵断面为傅里叶级数形式,可直观显示线路中的波长成分,为控制振动加速度带来了方便。如前文所述,为使线路纵断面中波长成分大于敏感波长,傅里叶级数阶数应小于1 428/200≈8阶;此外,经过试算,当阶数至少为4阶时,优化模型才可满足约束条件,此时线路纵断面的波长成分可由式(2)计算得到,如表1所示。

表1 优化线路纵断面波长成分(4阶)Tab.1 Wavelength component of optimized railway profile (order 4)

3.2 纵断面优化效果

在表1波长成分下,超大跨度悬索桥上优化后的纵断面如图5所示。图5(a)中道床厚度330,450 mm表示当道床厚度为330,450 mm时纵断面的高程,优化纵断面高程始终位于此区间,代表各里程点均满足道床厚度要求。优化后的线路纵断面与实测桥梁线形并非有完全相同的变化趋势,与一般线路设计尽量“贴合”桥梁线形的方式相比,显示了线路方案的多样性。

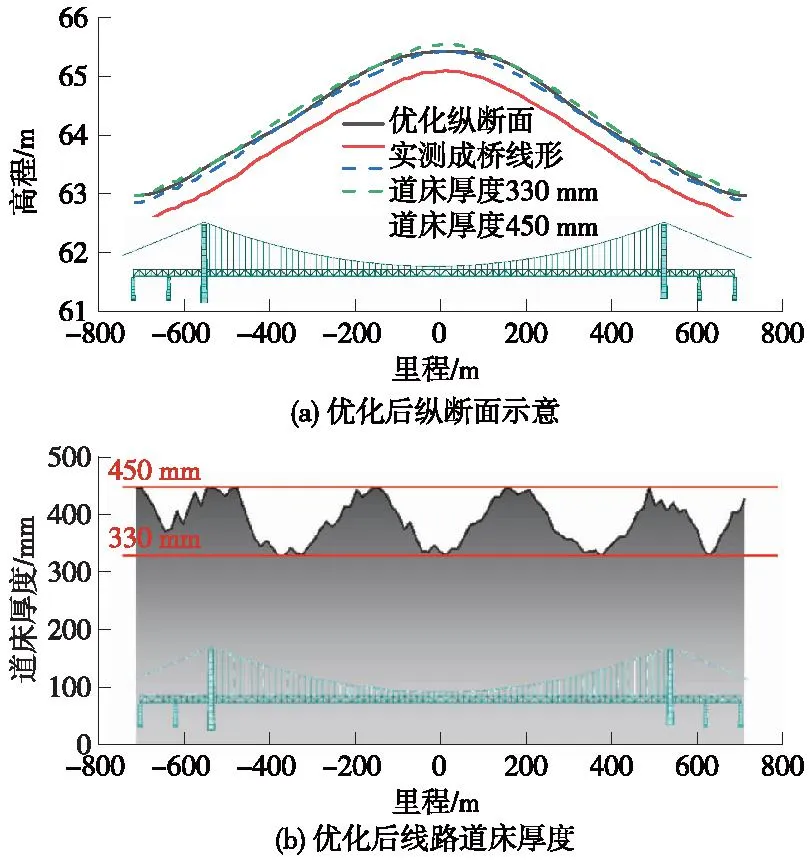
图5 线路纵断面优化效果Fig.5 Optimization effect of railway profile

列车以250 km/h通过优化纵断面的动力响应如图6所示,图中离心加速度由式(4)、式(5)计算得到。优化纵断面加速度在-0.1～0.15 m/s2波动,加速度平稳变化,少有较大突变;多坡段纵断面加速度在-0.3～0.3 m/s2波动,并且在变坡点处有明显突变。从行车舒适性上看,傅里叶级数形式纵断面明显优于多坡段纵断面,并且加速度峰值远小于《铁路线路设计规范》中乘客舒适度允许的竖向离心加速度0.4 m/s2的取值。此外,优化纵断面的加速度与离心加速度吻合较好,说明优化纵断面的列车加速度主要由离心加速度组成,通过对线路纵断面函数阶数的控制,减小了车体振动加速度的影响。一方面验证了仿真模型的正确性及优化模型的合理性,另一方面也说明可直接通过纵断面函数大致预测加速度响应,为纵断面设计带来方便。

图6 优化纵断面垂向加速度Fig.6 Vehicle vertical acceleration in optimized railway profile

为分析优化后纵断面平顺性对桥梁变形的适应性,将优化纵断面与桥梁整体升降温线形叠加,使用10 m中点弦测法输出弦测值,如图7所示。优化后纵断面线形平顺,弦测值分布与加速度响应分布相似;叠加桥梁整体升降温线形后,桥塔处的弦测值发生较为明显的突变,且随温差变大逐渐变大,说明桥梁整体升降温工况会对纵断面的平顺性产生一定影响。

图7 不同温度下优化纵断面弦测值Fig.7 Chord measurement value of optimized railway profile under different temperatures

由于优化纵断面只存在长波成分,而桥梁整体升降温的竖向变形也为匀顺的长波曲线,因此叠加后的纵断面也只存在长波成分,线形圆顺。叠加桥梁工况后纵断面线形弦测值最大不超过0.4 mm,远小于TB10621—2014《高速铁路设计规范》中限值2 mm、TG/GW 116—2013《高速铁路有砟轨道线路维修规则(试行)》中限值3 mm,说明优化后的纵断面满足平顺性要求,且对桥梁变形有较好的适应性。

3.3 关于模型阶数的讨论

如前文分析,该超大跨度悬索桥纵断面的傅里叶级数阶数N应取为4～7阶,然而不同阶数会产生不同的线形方案,从而影响列车的动力响应。进一步求解不同阶数下的线路纵断面,分析阶数的影响,各阶纵断面的波长成分如表2所示。由于最小波长均大于车体敏感波长,因此可将离心加速度作为列车的加速度响应,结果如图8所示。

表2 不同阶数线路纵断面的波长 mTab.2 Wavelength of railway profile under different order

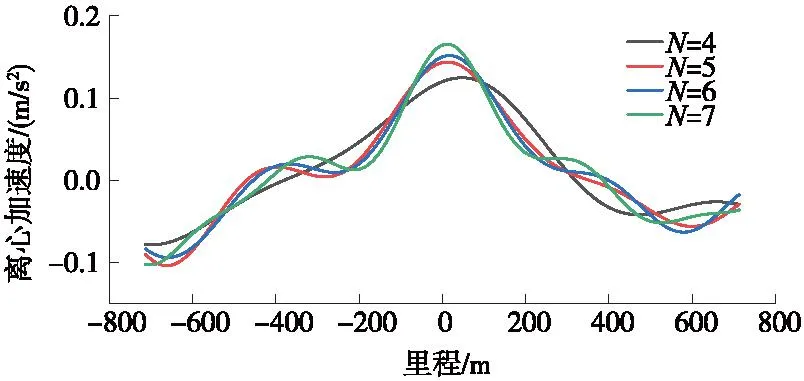
图8 阶数对纵断面离心加速度的影响Fig.8 The influence of order on the centrifugal acceleration of railway profile

不同阶数的傅里叶级数呈现不同的纵断面方案,但均可满足道床厚度及行车要求。随着阶数的提升,车体响应分布出现了更多的波动,原因在于阶数的提升引入了更多较短的波长,产生了更多不同半径的曲线。从幅值上看,离心加速度对阶数并不敏感,阶数的提升不会带来列车响应的明显减小。因此,当纵断面中的最小波长大于车体敏感波长时,阶数与列车响应没有明显的相关性。为使线形简单、更加可控,实际工程中建议选取较小阶数即可。