尺规作特殊图形的构图思路探析

摘" 要：以2024年中考江苏南京卷第26题为例，通过结构分析、模型联想，探析不同作图方法的构图思路，挖掘试题中蕴含的教学价值，并借助变式拓展，深研此类作特殊图形的问题，揭示其通性通法，促进对作图研究和推理教学的思考.

关键词：尺规作图；构图思路；通性通法

中图分类号：G633.6" " " 文献标识码：A" " " 文章编号：1673-8284（2025）01-0053-05

引用格式：郭源源. 尺规作特殊图形的构图思路探析：从2024年中考江苏南京卷第26题谈起［J］. 中国数学教育（初中版），2025（1）：53-56，64.

尺规作图是数学文化长廊中一颗璀璨的明珠，它以直观的方式、开放的思路、严密的逻辑成为数学教学中独具一格的教学内容. 在众多作图题中，有一类题为作已知图形的特殊图形，它对图形特征的分析要求更缜密，对构图的思路要求更灵活，不仅可以考查学生对基本模型的掌握程度，还可以考查学生的发散思维能力，给人一种简约而不简单之感. 以2024年中考江苏南京卷第26题为例，对这类作图题的解法、结构和拓展进行探析，供同行研究参考.

一、试题呈现

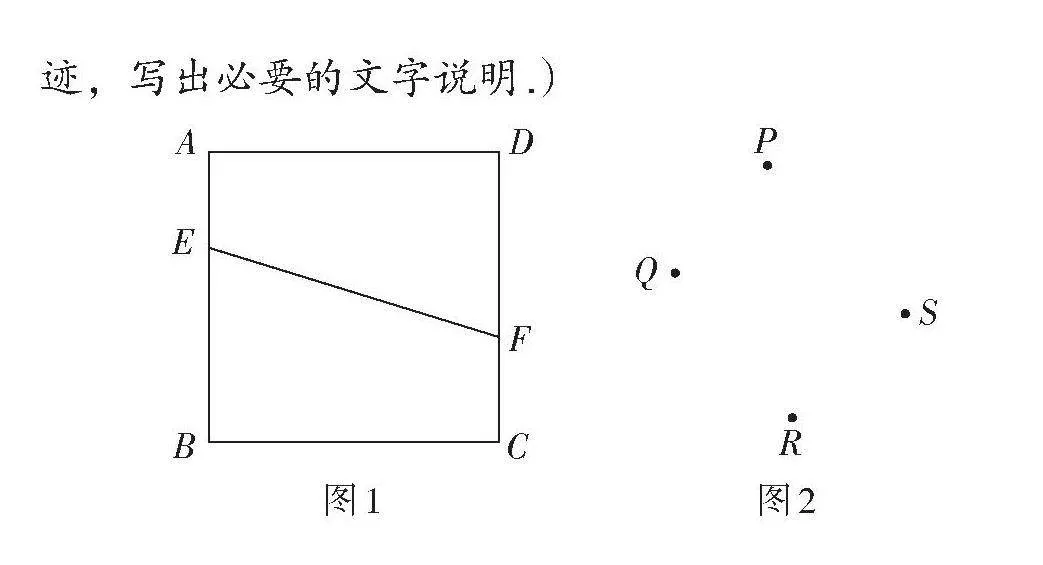
题目 （1）如图1，点E，F分别在正方形ABCD的边AB，CD上，连接EF. 求作GH，使点G，H分别在边BC，AD上（均不与顶点重合），且[GH⊥EF].

（2）已知点P，Q，R，S的位置如图2所示，若它们分别在一个正方形的四条边上，用两种不同的方法求作正方形过点P的边所在的直线.

（要求：① 用直尺和圆规作图；② 保留作图的痕迹，写出必要的文字说明.）

[图1] [图2]

二、解法探究

该题第（1）小题较为基础，本文只探究第（2）小题的作法.

1. 关联问题，联想“十字形”构图

由第（1）小题的作图可以发现正方形中的“十字形”模型，即只要[GH⊥EF]，则有[GH=EF]；同样，只要满足[GH⊥EF]且[GH=EF]，也容易证明四边形ABCD是正方形. 由此，对于第（2）小题，只需要瞄准“十字形”构图，就一定能作出正方形，从而产生作法1.

作法1：如图3，连接QS，过点R作[RP′⊥QS]且[RP′=QS]，得到点P′. 连接PP′，直线PP′即为所求.

[图3]

需要说明的是，图中给定的4个点P，Q，R，S并不是标准的“十字形”，所以部分学生看到PR与QS不垂直，就避开了这种思路. 其实，此思路还可以通过“弱化条件”来理解，弱化点P，只剩点Q，R，S，由这3个点搭建出“十字形”，然后只要作垂直围成四边形，则此四边形一定是正方形，而这样的正方形有无数个，最后考虑正方形还要过点P，所以直线PP′即为所求. 同理，还可以先作正方形过其他3点的边所在的直线，再通过垂直或平行确定过点P的边所在的直线.

2. 基于给定的点，计算线段长度，量化构图

由给定的4个点，可以联想哪些元素是确定的. 容易想到的就是线段PR，QS的交点O确定，线段OP，OR，OQ，OS确定. 如图4，若能围成正方形，则[OM+ON=QS]，[OMON=OPOR]，可以得到[OM=QS ⋅ OPPR]，即OM为定长. 故只需要构造相似三角形得到OM的长，截取OM的长即可确定点M，从而产生作法2.

[（a）] [（b）][图4]

作法2：如图4（a），连接PR，QS，PR与QS交于点O. 如图4（b），作与图4（a）中线段PR和线段QS等长的线段，使点P与点Q重合，连接RS，过点O作[OT∥RS]交QS于点T，则QT即为OM的长. 如图4（a），过交点O作QS的垂线，并截取[OM=QT]. 连接PM，直线PM即为所求.

需要说明的是，这种作法仍然用到了“十字形”模型，只是将作法1中作点R处的RP′换成作点O处的OM，属于“十字形”等长的比例化作图. 考虑到点O也是一个特殊的位置，从此处突破具备合理性，故将此作法单独列出.

3. 尝试画图，利用归纳猜想发现定点构图

若过Q，R，S这3个点画正方形（点Q，R，S要分别落在正方形的三边上），则有无数个正方形满足要求，猜想这些正方形的规律. 如图5，尝试多画一些经过点Q，R，S的正方形，就可以发现这些正方形的第四条边都经过一个定点M，从而产生作法3.

[图5]

作法3：如图5，过点Q，R，S任意作两个正方形，这两个正方形的第四条边交于点M，连接PM，直线PM即为所求.

虽然尺规作图的方法最终要回归到“明理”的要求上去，但产生作法的思维过程则更直观、感性和活泼. 尽管此作法有点“猜”的味道，但对于探究性问题，在不清楚结论的情况下，经历“尝试—归纳—猜想—证明”的过程是符合认知逻辑的. 所以尺规作图的思路可以从“有理”开始，也可以从“无理”开始.“有理”重依据，“无理”重直观，各具优势. 这也是尺规作图题的魅力所在. 作法3的最终证明等价于作法1中“十字形”模型的证法，但它的思路是从“无理”到“有理”的过程，是合情推理的体现. 这种解决问题的思维方式是值得推荐的.

4. 紧扣直角，利用正方形对角线性质构图

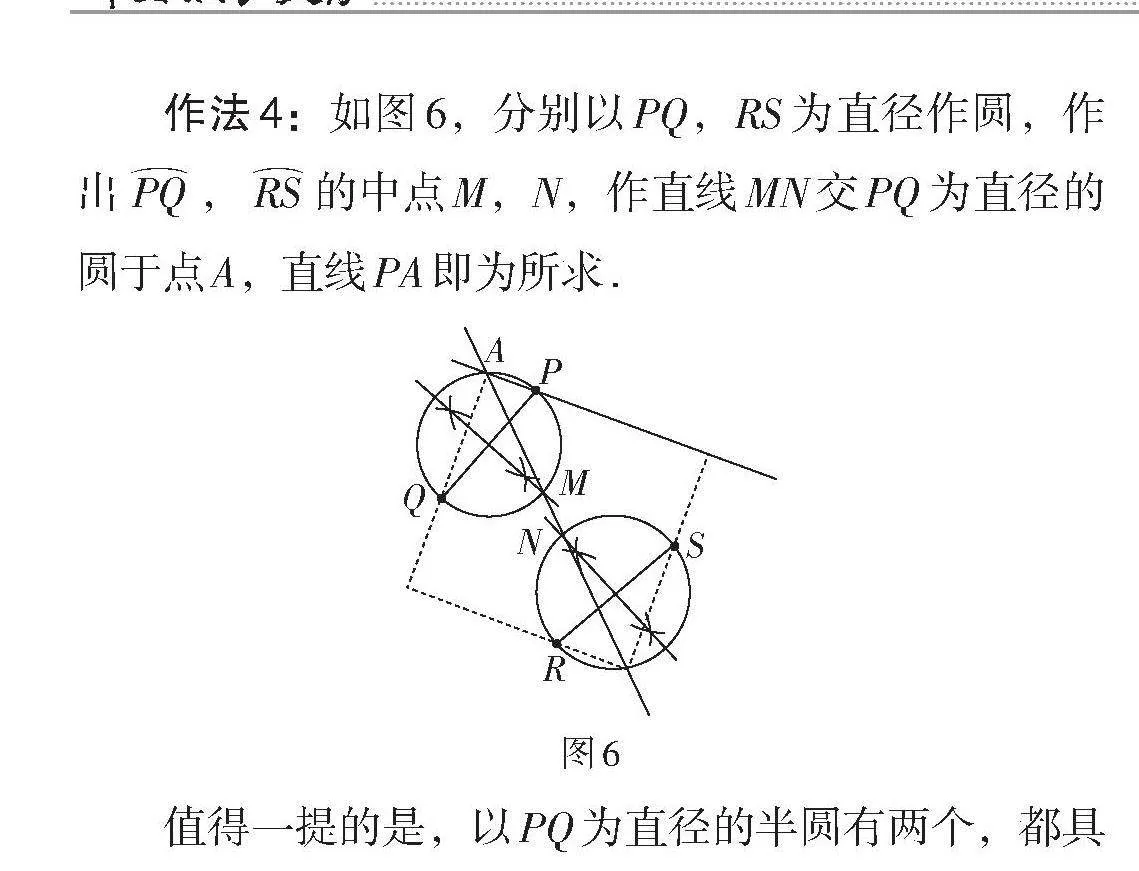
若能作出四边形PQRS的外接正方形，则四条边向外所对的角一定为直角，易联想到圆周角定理，故分别以PQ，QR，RS，SP为直径作圆，这样过点P任意画一条直线，与圆相交后顺次围成的四边形一定是矩形. 若能再强化“对角线平分对角”，矩形即可变为正方形，所以只需对角线过[PQ]和[RS]的中点，就能达成这样的效果，即产生作法4.

作法4：如图6，分别以PQ，RS为直径作圆，作出[PQ]，[RS]的中点M，N，作直线MN交PQ为直径的圆于点A，直线PA即为所求.

[图6]

值得一提的是，以PQ为直径的半圆有两个，都具有中点，但试题中要求P，Q，R，S皆为正方形边上的点，不可以在边的延长线上，所以[PQ]，[RS]的中点M，N只能在正方形的内部. 若从以PS，QR为直径作圆突破，方法亦是同理.

5. 弱化条件，借助旋转变换和相似构图

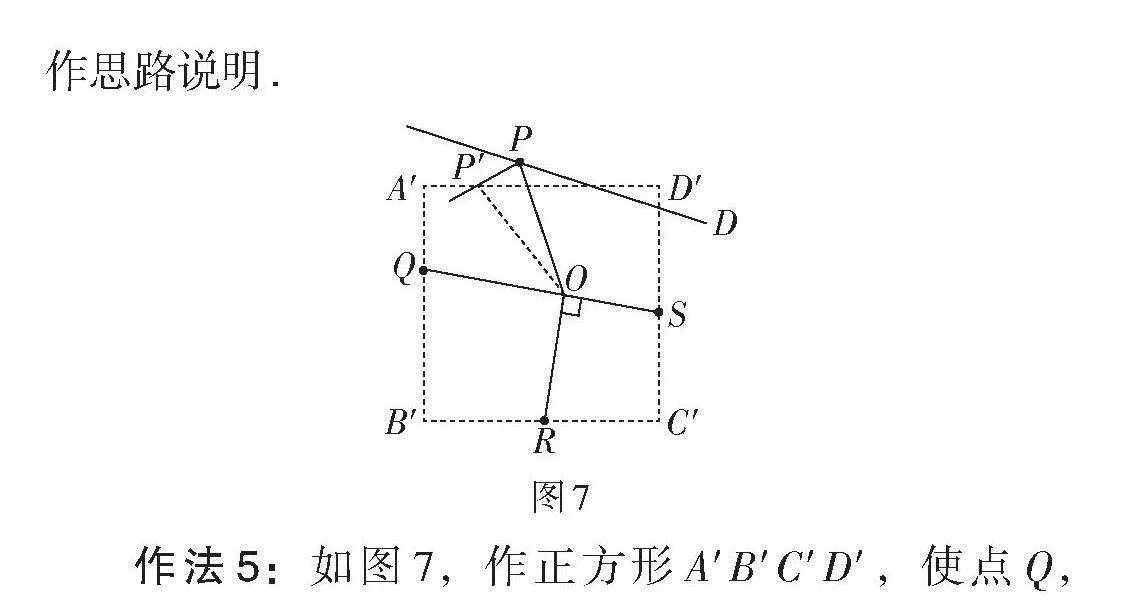
作已知四边形的外接正方形，能否反过来想呢？即给定一个正方形，能否作一个内接四边形与已知四边形相似呢？这两个问题是等价的. 若能作出，则根据角度关系即可得到过点P的边所在的直线.

借助“弱化条件 + 旋转变换”是可以作出的. 先弱化点P这个条件，则能作出无数个过点Q，R，S的正方形，只要任意作一条过点R的直线，再分别过点Q，S作过点R的直线的垂线，然后截取邻边相等即可得到图7中的正方形A′B′C′D′. 接下来要寻找到相似中心，让点Q，R，S在三边上动起来时，能确保四边形PQRS的形状不变. 由于点Q的路径与点R的路径方向夹角为90°，点R的路径与点S的路径方向夹角也为90°，根据旋转相似可知点Q，R的路径夹角与∠QOR相等（点O为相似中心）. 故[∠QOR=90°]. 同理，[∠SOR=90°]. 根据以上分析，过点R作QS的垂线，垂足即为相似中心O. 只需要以点O为中心旋转，就可以将点P转移到边A′D′上，即作[∠OPP′=][∠OQB′]，PP′交A′D′于点P′，然后点Q′，R′，S′的位置就能随之确定，即内接四边形P′Q′R′S′可作. 最后由∠OP′D′确定，只需要作[∠OPD=][∠OP′D′]，则PD即为原题中所求直线. 由于此作法弧线痕迹太多，会影响学生对图形的理解，此作法中只作思路说明.

[图7]

作法5：如图7，作正方形A′B′C′D′，使点Q，R，S分别在边A′B′，B′C′，C′D′上. 过点R作[RO⊥][QS]，垂足为点O. 作[∠OPP′=∠OQB′]，PP′交A′D′于点P′. 作[∠OPD=∠OP′D′]，直线PD即为所求.

此作法与前4种作法相比，难度较大，需要学生对旋转变换有深刻的理解，特别是对动点路径与相似中心的关系理解. 至于点Q，R的路径夹角为什么与∠QOR相等（点O为相似中心），在文献［2］中已证明. 如何根据路径方向或路径长的比寻找相似中心，在文献［3］中也已说明，这里不再赘述. 至于此四边形相似的证明，可以转化成三角形，只需要证明点Q，R动起来时，△QOR的形状不变即可，借助“旋转双相似”很容易证明，读者可自行尝试.

三、试题评价

1. 低起点，高立意——紧贴课程标准，立足素养

《义务教育数学课程标准（2011年版）》将尺规作图置于点、线、面、角、三角形、四边形、圆等基本几何图形之后，尺规作图内容也被列在一起集中呈现，成为了一种学习任务，其在帮助学生理解几何概念与实际操作等方面的功能被削弱.《义务教育数学课程标准（2022年版）》（以下简称《标准（2022年版）》）采用了“化整为零”的方法，将尺规作图融入线段、角、三角形等几何研究对象中，目的是让学生通过具体的操作活动，经历几何对象的图形构造过程，理解图形的组成元素之间的关系与结构，培养学生的几何直观. 所以《标准（2022年版）》在初中阶段的“尺规作图”部分新增了以下表述：通过尺规作图等直观操作的方法，理解平面图形的性质与关系；经历尺规作图的过程，增强动手能力，能想象出通过尺规作图的操作所形成的图形，理解尺规作图的基本原理与方法，发展空间观念和空间想象能力. 由此可见，尺规作图不再是一种显性的学习任务，而是一种理解几何元素之间“确定性”关系、剖析图形特征、构图等隐性功能的体现.

作为几何解答题，上述中考试题第（1）小题起点低，第（2）小题思维含量较高，两道小题都采用了尺规作图的考法. 整道试题看似从头到尾没有提到图形的性质、判定、元素关系等字面证明，仔细分析，却又发现处处都指向图形特征、性质、判定、元素关系的推理. 这种将推理化“有形”为“无形”的考法，形式新颖，大道至简，立意高远，彰显了尺规作图作为一种探究方法与认知策略的学习价值，以及对于发展学生数学核心素养的重要性.

2. 重关联，促联想——结构精致，考查思维

数学的思维是重逻辑的，数学试题也应该是蕴含逻辑的，特别是问题串之间应有紧密的关联，但这种关联要把握“搭台阶的尺度”. 台阶太高，思维跟不上，就变成了无效关联；台阶太低，“投喂”太明显，思维含量低，就变成了低效关联. 因此，尽管该题与“十字形”有关联，但第（1）小题并没有要求学生直接证明正方形和“十字形”的关系，而是采用了“作垂直”的考法，借助作出的图形，通过几何直观唤醒学生相关的知识储备，促进学生联想模型，为第（2）小题的作法打好铺垫，整个流程条理清晰，关联也恰到好处. 同时，第（1）小题的垂直构造方法有很多，如作垂直、作线段垂直平分线、截长构造“十字形”、构造全等三角形、作外接圆等，这些都能达成目标，入口很宽，方法多样；第（2）小题既有前一小题垂直的影子，也注重了条件的隐含性，考查了学生的模型联想能力、关联构图的能力和问题解决的能力，每一处都在考查学生思维的层次性. 该题结构非常精致，作图从不唯一到唯一，从直接作图到分析构图，从显性技能到隐性能力，重关联，促联想，层层递进，环环相扣，起到了良好的导向作用.

3. 借多法，巧分层——注重选拔，凸显价值

中考兼具“两考合一”的功能，既要重视基础，也要重视选拔. 每一道试题的命制，既要让大部分学生能入手得到分，也要让思维层次更高的学生得更多的分，所以区分度很关键. 为了有效区分不同学生的思维层次，第（2）小题要求用两种不同的方法作图. 第一种作法指向第（1）小题的“十字形”模型，是学生模型联想能力和关联构图能力的体现，属于“从有到有”；第二种作法没有任何指向，要学生想方设法自行另辟蹊径解决问题，是学生发散思维能力和问题解决能力的体现，属于“从无到有”. 在第（1）小题到第（2）小题中的两种作法中，从简单作图到联想转化，再到发散创造，难度逐渐上升，兼顾了不同学生的思维层次，让试题具有一定开放性的同时，也达成了选拔的功能，凸显了试题“两考合一”的价值.

四、教学启示

1. 明确课程目标，领悟尺规作图的价值

史宁中教授曾提出，用几何解释代数的基本理论工具是几何作图，几何作图蕴含着几何证明，对培养几何直观是非常有利的.《标准（2022年版）》强化了尺规作图和几何直观，它的价值主要表现在以下方面. 首先是培养学生问题解决的能力. 尺规作图是将数学推理与问题解决相融合，让推理贯穿整个过程，在解决问题过程中借助尺规作图进行分析、构图、判断、验证、推理，尤其是解题过程中遇到困难时，需要利用尺规作图厘清条件，这是明确问题解决的关键. 其次是建构几何知识体系.《标准（2022年版）》为落实学生核心素养，提出课程内容结构化的要求，重点是对内容结构化整合，而尺规作图恰恰可以有效实现知识的结构化，建构几何知识体系，利用尺规用多种方法作图，如作角平分线、作平行线、作等腰三角形、作平行四边形等，借助尺规可以将所有相关知识紧密联系起来，形成联想链，使得知识系统化、结构化. 最后是拓宽几何探究路径. 作图的本质还是回归到几何图形的性质和图形元素之间的关联，所以尺规作图是在帮助学生感知构图的合理性，帮助学生理解图形的结构特征，助力学生感悟图形的存在性和确定性. 其实构图的过程就是解题的过程，因此它拓宽了几何问题的探究路径.

2. 瞄准思维生长，回归尺规作图的要位

既然《标准（2022年版）》强化了尺规作图，那么教师有必要思考该如何教学尺规作图. 作图的思考策略往往可以分为两大类. 一类是“从有到有”，即基于基本模型进行作图，如原题中的作法1和作法2；另一类是“从无到有”，就是没有基本模型，先画草图，紧扣关键特征，执果索因，将几何元素先后确定，如原题中的作法3、作法4和作法5. 不管是哪一类，它的难点都不在于程序化的操作本身，而在于作图之前对目标图形的认识、拆解、分析、推理的过程. 因此，笔者认为，尺规作图的要点在于作图前的分析过程，其价值胜过作图，是作图中至关重要的环节. 教师要引领学生厘清已知条件与目标图形的关系，并经历以下的思维过程：（1）假设存在，画出草图，剖析图形中蕴含的数量关系和位置关系；（2）结构联想，关联模型，联想到常见的几何图形的性质或基本模型上；（3）基于确定，尝试构图，构思各元素确定的先后次序，初步规划作图步骤；（4）若条件复杂，图形难以确定，则借助弱化条件，再利用变换关联目标图形，还可以借助量化长度，利用计算出的线段长构图，从而确定点的位置. 总之，整个过程中，要将教学发力点落在作图思路的形成上，注重整个思维生长的过程，既要让学生“知其然，知其所以然”，更要“何以知其所以然”. 因此，教学中可以将尺规作图和推理能力核心素养相结合，并依此促进推理能力教学的优化，这种方式具有一定的前瞻实践意义.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］郭源源. 旋转位似“似”成双" 定点定形“轨”一致［J］. 教学月刊·中学版（教学参考），2020（10）：11-15.

［3］郭源源. 借助“相似中心”构图" 探寻“定角定比”路径：从一道中考几何最值题谈起［J］. 中小学数学（初中版），2024（3）：17-19.

［4］史宁中. 数学思想概论：图形与图形关系的抽象［M］. 长春：东北师范大学出版社，2015.

基金项目：江苏省“十四五”教育科学规划课题——培育学生系统思维的初中数学章统领课教学研究（D/2021/02/24）.

作者简介：郭源源（1988— ），男，中学一级教师，主要从事初中数学课堂教学设计和解题教学研究.