基于系统动力学的政策成效与预见仿真方法探析

摘 要： ［目的／ 意义］ 系统动力学的仿真模拟能够全面捕捉政策影响下的复杂社会系统动态性， 准确模拟政策干预随时间推移的累积影响， 评估政策的实施效果， 对于推动政策工具科学高效地制定和使用， 以及提高政策效能都有着极其重要的作用。［方法／ 过程］ 以人口生育政策实施为样例， 基于生育率等关键性影响因素与教育经济等环境影响参数， 借助Ｖｅｎｓｉｍ ＰＬＥ 构建一套系统动力学仿真模型， 动态演示人口—政策—经济子系统间的交互， 设计执行３ 项差异化政策干预情景， 深入模拟预测不同政策导向下的人口变迁路径与演化趋势。［结果／结论］ 研究发现， 生育政策的放宽在促进人口增长的同时， 有效缓解老龄化趋势。但政策影响日渐式微， 亟需结构化变革与调整。

关键词： 系统动力学； 仿真； 政策成效； 人口生育政策

ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１００８－０８２１．２０２５．０１．００１

〔中图分类号〕Ｇ２０３； Ｎ９４１. ３； Ｃ９２４. ２１ 〔文献标识码〕Ａ 〔文章编号〕１００８－０８２１ （２０２５） ０１－０００５－１３

预见并跟踪评估政策实施成效， 在政策决策与实施中有重要现实意义。在以往政策评价研究中，基于统计因果的政策成效评估与回归计量方法， 比如Ｌｅｓｌｉｅ 方程、Ｌｅｓｌｉｅ 修正模型、ＡＲＩＭＡ 时间序列预测等往往聚焦部分变量， 导致模型可能遗漏大量外部变量、弱相关关系， 无法观测变量的动态交互效应， 在作用机理上难以表征变量间的闭合反馈，无法持续呈现或评估政策行为与实施成效的动态关系。以人口政策为例， 人口规模和生育水平与经济水平、社会服务、教育供给、家庭结构、社会观念等多因素相关， 而自变量间也存在相互影响、关联，传统计量与回归方法在分析政策作用机理、影响因素、政策成效等方面都存在困难。因此， 在人口生育和预测领域， 随着计算人口学和主体建模技术的日益成熟， 一方面， 世界各国（地区）建立了完备的人口统计体系和人口数据库， 如联合国世界人口政策数据库； 另一方面， 大型人口仿真系统相继引入，比如ＭＩＭＯＳＥ、ＭＬ３、ＪＡＳ－ｍｉｎｅ、中国人口与发展研究中心的ＰＡＤＩＳ 决策模型、国际通用人口预测软件ＰＡＤＩＳ—ＩＮＴ 等， 在人口预测、婚育过程、家庭关系、迁移、养老支持、家庭政策等人口学领域得到广泛应用［１］ 。

针对传统方法局限特定领域或单一变量间的交互， 而未能充分捕捉政策干预的多维影响和动态反馈机制的缺陷， 依托人口学和社会学相关理论， 本文提出构建了一个涵盖多变量、强交互的“人口—政策—经济” 仿真模型， 不仅纳入传统模型中的人口变量， 还特别注重变量间的动态交互与反馈效应，在此基础上， 设计并执行３ 项差异化政策干预情景，模拟预测人口变迁路径与演化趋势。

１ 研究回顾

１. １ 人口及其影响因素研究

人口是促进社会进步和生产发展的主体， 是社会的重要组成部分。广义上说， 人口学包含一切与人口变动相关的理论。１８ 世纪， 马尔萨斯［２］ 提出“人口原理”， 指出人类必须控制人口增长， 人口问题开始得到重视。２０ 世纪５０ 年代， 冯玉祥［３］ 提出中国人口问题“非增即减” 的特质， 为中国人口理论研究奠定了基础。

人口研究重点关注出生率、年龄、性别、就业、人口比例等具体指标， 目的是解决出生率调节、老龄化应对、性别失衡、家庭结构混乱等关切问题。在人口观察中， 西方和东亚国家（地区）整体表现为低出生率、低增长率、低生育率， 存在少子化老龄化问题［４］ 。老龄化涉及面广［３］ ， 不仅影响劳动力市场［５］ 、社会保障［６］ 、居民消费［７］ 、财政负担［８］ 、经济持续增长［９］ 等可持续发展指标， 而且会改变家庭结构， 抑制生育意愿［９］ 。

政策调整是人口变化的主要原因， 生育政策直接影响人口的数量和结构［１０］ 。除政策外， 经济、教育也是影响人口变化的关键因素， 居民消费价格指数、居民人均收入［１１］ 、受教育水平［１２］ 等经济政策因素显著影响出生率。医疗水平、人力资本水平、生育保险对人口出生率同样有影响［１３］ 。此外，移民政策与区域人口流动也会影响生育率［１４］ ， 进而影响人口变动。

１. ２ 生育政策研究

生育政策被视为调控人口指标、促进经济社会发展的关键。迄今为止的研究主要聚焦于生育政策所引发的人口问题及其外部影响两大维度。

人口问题方面， 积极的生育政策能缓解劳动力压力、遏制老龄化加速， 但政策效应存在时限［１５］ 。计划生育政策减轻了总劳动负担［１６］ ， 但提前了老龄化［１７］ ； 独生子女政策导致男性人口大幅提升［１８－１９］ 。性别比例失衡， 导致“婚姻挤压” 及后续养老问题显现［２０］ 。严格落实生育政策能提高女性就业机会，但生育假期及过松的福利支持则会提升女性就业成本， 加重就业歧视［２１］ 。

生育政策通过调节人口结构， 对经济、社会、教育产生巨大影响。经济层面， 完全二孩政策或相关生育激励措施可能会提高住房市场需求［２２］ 。社会层面， 社会养老保障体系的承压状况［２３］ 与人口峰值［２４］ 等问题， 也破坏社会结构和经济发展。教育层面， 政策通过家庭福利补贴、税收优惠、育产假、托幼服务、促进就业性别平等的政策支持来减轻家庭教育成本。

１. ３ 系统动力学人口仿真

１９５６ 年， Ｆｏｒｒｅｓｔｅｒ Ｊ Ｗ［２５］ 为分析库存管理问题创造系统动力学， 通过构建模型和输入输出速率方程， 研究系统内部结构。起初， 系统动力学主要应用于企业管理， 用以解决市场原料和商品库存等的生产、运输、传送问题［２６］ 。随着相关理论的健全发展， 应用范围不断扩大， 涉及社会［２７］ 、政治［２８］ 、生态［２９］ 、经济［３０］ 等各个领域。

政策仿真方法可以较好地应对社会结构的复杂性［３１］ 。从方法类型看， 包括模特卡洛抽样、博弈论、ＤＳＧＥ（动态随机一般均衡模型）、元胞自动机、系统动力学、多主体仿真、神经网络预测、综合仿真推演与情景模拟、政策沙盘（兵推系统）、数字孪生与数字剧场等多种方法； 从应用领域看， 主要包括微观层的数值模拟、仿真计算， 中观层的模型仿真、因果推理， 宏观层的系统动力模型、政策生态建构与远期预见等应用场景。

在人口领域， 大量关联因素或情景变量被引入系统仿真模型。针对人口结构的仿真研究广泛采纳年龄分层与性别区分框架， 如： 依据生命周期划分青年、成年、中年、老年４ 个年龄段［３２］ ； 结合性别差异以５ 年为年龄间隔细分人口［３３］ ； 三阶及以上老化链模型的构建［３４］ 等， 为人口动态仿真分析提供了强有力的理论工具和方法论支撑。

就具体研究而言， 李香霞［３５］ 设定低、中、高三档政策干预情景进行江苏省人口仿真预测， 使不同政策组合的效应预见成为可能。朱墨蕤等［３６］ 集合人口、财政及经济活动子系统， 深入探讨经济增长如何响应并影响人口老龄化进程， 强调经济系统对人口结构变化的适应性和反馈机制。刘靖等［３７］ 构建区域经济转型升级与教育体系协同发展模型， 揭示教育水平对劳动力结构优化和经济结构转型升级的推动， 进一步验证教育在人口—经济系统中的催化功能。

１. ４ 研究述评

尽管当前学界已在相关领域的研究中取得显著进展， 但仍存在研究局限与空白。

在人口及其多元影响因素的研究范畴内， 大量文献针对出生率、年龄结构、性别比例等核心指标进行了详尽探讨， 但多数研究仍采用孤立变量的分析方法， 未能充分揭示其复杂互动机制及对人口动态变化的系统性影响， 导致对人口发展趋势的全面理解不足， 难以精准预测未来人口结构变化。

有关生育政策的研究多聚焦特定政策情境下的短期效应分析， 缺乏对不同政策组合及其长期效应的系统性、综合性评估。同时， 对生育政策与社会经济系统、教育体系等关键领域的相互作用机制的研究尚显薄弱， 限制了政策制定者在制定和调整生育政策时的精准度和科学性。

尽管已有大量研究利用系统动力学方法对人口结构进行仿真预测， 但现有模型在构建过程中往往对外部环境因素（如政策变动、经济波动等）进行了简化处理， 导致模型在预测人口趋势和政策响应时产生较大偏差， 降低模型的实用价值和预测准确性。

本研究创新性地融合政策、经济、人口三大关键领域， 构建综合性系统动力学仿真框架， 深入剖析不同政策组合对我国人口结构的多维影响， 深化对生育政策效应的全方位理解， 旨在提供更为细腻全面的分析视角， 为制定更加科学合理的政策提供坚实的理论支撑与实证基础。

２ 人口生育政策效应的人口预测仿真模型

构建人口生育政策仿真模型， 须先行设定以下假设： ①微量迁移假设： 在非移民国家， 若迁移人口占总人口基数比值极小， 则忽略迁入迁出影响。②稳态社会发展假设： 排除突发重大灾害、战争、疾病等非常态事件干扰， 假设社会经济环境持续平稳发展。③全国同质性假设： 假设全国范围内生育模式与死亡模式一致， 不存在区域差异。

２. １ 模型框架

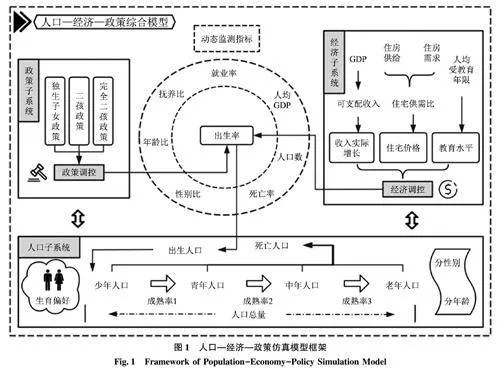
在以往研究［１５，３８－４０］ 中， 经济波动、政策导向与人口结构变动之间存在相互影响与动态平衡。基于此， 本文提出“人口—政策—经济” （ＰＰＥ） 综合模型框架， 如图１ 所示， 包含人口变迁、政策调控、经济发展三大动态子系统， 通过出生率指标形成反馈闭环。其中， 人口子系统以改进后的高阶老化链人口模型为基础， 划分少年、青年、中年、老年，分别代表０～１４ 岁、１５～４９ 岁人口、５０～６４ 岁人口、６５ 岁及以上人口， 成熟率即为各年龄段间的转移人口比例。研究重点监测人口规模、年龄结构、出生率、死亡率等关键指标。其中， 政策调整、经济波动对人口结构特征、抚养比率等在内的多元化监测指标进行互动关联， 而人口的规模变化反馈至其他子系统， 形成闭合互动链。政策子系统以现行生育政策调整为依据， 分别模拟独生子女政策、独生子女家庭二孩政策（后称“二孩政策”）、完全二孩政策的不同模态， 并测算政策调控对人口系统、经济活动产生的直接或间接影响。尤其是人口出生率与政策子系统、经济子系统关联密切， 形成即时反馈回路， 用于评估政策实践、人口动态与经济走势间的互动张力与协同效应。经济子系统选择国内生产总值（ＧＤＰ）增长、住房市场、教育水平等观测维度， 经济发展影响居民收入和消费水平， 进而影响人口出生率生育决策和人口结构。具体通过就业率、人均ＧＤＰ 及住房价格等经济指标进行模型拟合。

通过政策仿真与动态监测， 可以考虑使用就业率反映劳动市场健康度、人均ＧＤＰ 反映经济繁荣程度、人口结构和抚养比反映家庭与社会支持压力等政策评估指标， 为人口生育政策的当下成效及未来影响提供更广泛、更持续的预测和决策依据。

２. ２ 因果关系设计

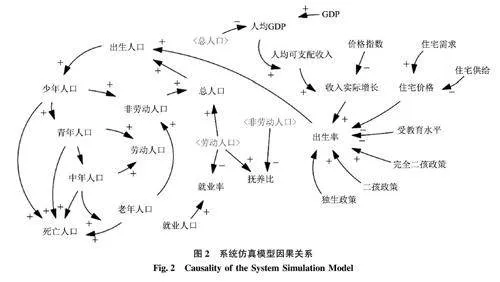
本文拟采用系统动力学方法（Ｓｙｓｔｅｍ Ｄｙｎａｍｉｃｓ，ＳＤ）进行仿真建模， 通过构建因果关系的反馈回路，揭示内部各变量间的关联逻辑、相互作用与影响路径， 揭示“人口—政策—经济” 交互作用的复杂性和非线性特征。具体到本模型中， 因果关系反馈图如图２ 所示。

在经济子系统中， 收入水平与育儿成本是关键变量。第一， 人均ＧＤＰ 水平提升促进居民可支配收入增长， 提升消费与储蓄， 从而提升生育意愿， 形成正向循环。第二， 住房供需比影响住房价格变动，而住房价格上升会提升育儿成本， 进而降低生育意愿。第三， 教育水平提升和教育成本上涨， 与生育意愿的下降趋势密切相关， 进而限制家庭规模扩张。

在政策子系统中， 人口生育政策调整是外部变量， 直接干预并影响到家庭的生育决策， 改变出生率。人口生育政策作为外部强制力， 通过法律和社会规范的手段， 直接作用于家庭规模的选择， 进而影响总人口结构。

在人口子系统中， 出生率与死亡率是关键观测指标。出生率作为连接各子系统的纽带， 直接影响出生人口数量， 影响人口结构的未来趋势和规模比例波动， 从而影响社会的劳动力供应、消费模式及养老负担等。劳动力市场供给的变化将进一步影响经济发展潜力， 消费模式的转型将进一步影响市场需求结构， 而老年人口比例的增加则将进一步加重社会保障体系压力。

２. ３ 结构流图设计

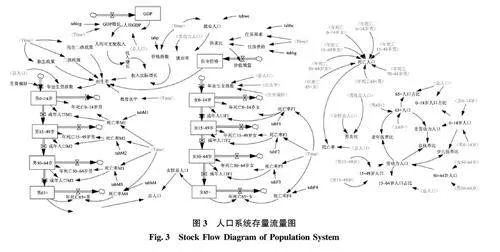
基于因果关系图， 进一步导入变量设计人口—经济—政策系统结构流图， 如图３ 所示。在结构流图中确认了１０ 个水平变量和１８ 个速率变量， 其中水平变量包括ＧＤＰ、住宅价格、各分年龄段分性别人口； 速率变量包括ＧＤＰ 增长量、住宅价格增长量、流动人口（包含出生人口、各分年龄段分性别转移人口）、各分年龄段分性别死亡人口， 其余观察变量作为常量设计。

在变量设计中， 政策变量包含独生子女、单独二孩及全面二孩政策３ 个虚拟变量， 用于量化政策影响。为实现对政策成效的即时监控与广泛评估，本文引入了男女比例、抚养比、劳动力与非劳动力人口比例、就业率等监测指标。其中， 总抚养比通过计算非劳动力人口相对于劳动力人口的比例， 用以衡量社会整体抚养负担； 而老年抚养比专注于评估６５ 岁及以上老年人口对劳动力群体的依赖度，子女抚养比则关注０～１４ 岁未成年群体的相应比例，二者共同描绘代际间的经济支持需求结构。

２. ４ 参数方程确定

１９８２ 年９ 月， 党的十二大把计划生育确定为基本国策。随后， “双独二孩” “单独二孩” “全面二孩” 等政策陆续出台。２０２１ 年， 政府进一步调整人口生育政策， “三孩政策” 落地。由于三孩政策颁布时间尚短， 存在政策延迟与数据获取问题， 不将其纳入研究范围。因此， 文本数据时间跨度为１９８２—２０２０ 年。

本文采纳核心数据体系主要分为两大类： 一是历史基准数据和参数方程（后称基础变量）， 旨在描摹系统内变量的相互作用， 主要用于模型拟合与参数调节， 提升模型预测的准确性。二是预测数据和虚拟数据， 对趋势前瞻性预测与组态差异下的仿真模拟， 预估未来发展轨迹。在数据来源方面， 主要采纳国家统计局的经济数据和人口普查数据， 辅以《中国人口和就业统计年鉴》补充相关就业信息。具体参数方程式设定如下：

２. ４. １ 经济子系统

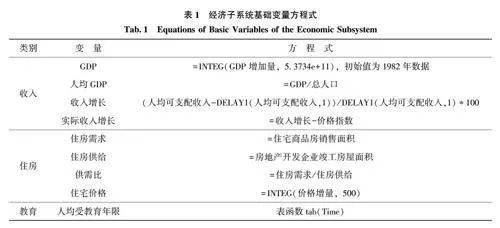
经济子系统的基础变量可以划分为收入、住房、教育三大类， 参数方程式如表１ 所示。

在人均受教育年限的评估中， 依据国家统计局确立的小学至高等教育的标准化年制（即小学６ 年、初中９ 年、高中１２ 年， 大专以上１６ 年）进行量化。通过拟合， 发现人均受教育年限与时间呈显著的对数关系， 模型拟合度极高， 可决系数Ｒ２ 为０. ９７３，可使用该模型进一步预测未来受教育年限（以博士研究生最高年限２２ 年为上限）。ＧＤＰ 增长、住宅销售面积、竣工房屋面积、价格指数具有一定波动性，因此采用ＡＲＩＭＡ（整合自回归移动平均）模型作为预测依据， 如ＡＲＩＭＡ（２，１，０）、ＡＲＩＭＡ（０，２，２）等模型的参数误差较小， 可用于上述模型预测。

综上， 上述变量的预测变量及方程如表２ 所示。

２. ４. ２ 政策子系统

自中华人民共和国成立以来， 我国生育政策历经多次调整： １９８２ 年前处于自然生育阶段， １９８２年后严格计划生育； ２０１１ 年底全国３１ 个省份均放开双独家庭二孩政策； ２０１３ 年“单独二孩” 政策正式落地； ２０１５ 年， 党的十八届五中全会提出推行“全面二孩” 政策并于２０１６ 年施行。考虑到“双独二孩” 到“单独二孩” 的政策过渡， 研究将二孩政策分析时间适当前置， 不只局限于“单独二孩”节点。引入虚拟变量表征政策， 确保模型输入与现实政策变迁保持同步， 如表３ 所示。

２. ４. ３ 人口子系统

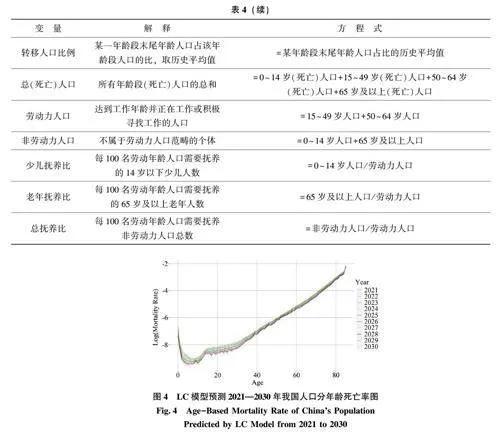
人口子系统包括但不限于出生率、死亡率、人口数量、分性别分年龄相关数据等。针对中国人口数据广泛依赖抽样调查的特点， 需对诸如出生人口、死亡人口等核心指标采用一定的校正策略。本文采用抽样比例还原方法从抽样数据中还原测算人口总规模。人口子系统的基础数据及方程如表４ 所示。

其中， 男女比例依据历史平均值界定为男孩０. ５４、女孩０. ４６； 年出生人数为总人口乘以出生率，年死亡人数为总人口乘以死亡率； 转移人口是相邻年龄段的过渡人口， 其比例取历史平均值， 表示某年龄段末尾年龄顺利流入下一段的人口； 劳动力人口包括１５ ～ ６４ 岁人口， 是经济活动主要参与者，非劳动力人口则是０ ～ １４ 岁和６５ 岁及以上人口。少儿、老年抚养比分别反映每１００ 名劳动力需抚养的０～１４ 岁少儿、６５ 岁及以上老年人数， 总抚养比则是两者之和， 全面评估社会抚养负担。

作为衡量人口动态演变的两个基本维度， 出生率与死亡率对理解和预测人口发展态势至关重要。构建方程时， 出生率与死亡率的预测既要考虑年龄结构、性别比例等内在变量， 也应考虑社会经济条件、政策导向等外在因素。

１） 死亡率预测

Ｌｅｅ－Ｃａｒｔｅｒ 模型作为死亡率预测的代表性模型，采用趋势外推法进行人口预测［４１］ 。该模型通过拆分年龄和时间效应， 动态描绘了各年龄段死亡率的时序变化， 其数学表达如式（１） 所示， 其中包含年龄效应、时间趋势及随机误差项。

ｌｎ（ｍｘ，ｔ ）＝ ａｘ ＋ｂｘ ｋｔ ＋εｘ，ｔ （１）

其中， ａｘ 为年龄效应参数， 捕捉了不同年龄段死亡率的基本差异。ｂｘ 为年龄相关的因子载荷，衡量不同年龄段死亡率随时间变化的敏感度。ｋｔ 为时间因子， εｘ，ｔ为误差项。

研究借助Ｒ 语言的Ｄｅｍｏｇｒａｐｈｙ 包， 运用ＬＣ 模型分析１９９６—２０２０ 年的死亡率数据， 设定８５ 岁为年龄上限。模型参数稳定性良好， 预测精确度高，体现为低均方误差（ＭＳＥ ＝ ０. ０８０）和较高的解释力（方差占比６３. ９％）， 其估算发现， 死亡率随时间递减的整体趋势， 尤其在幼童与老年群体中更为显著， 基本体现了医疗技术与健康服务的改善对死亡率的影响。在此基础上对未来１０ 年（２０２１—２０３０ 年）的死亡率趋势进行预估， 所得结果如图４ 所示。

此外， 本研究以历史平均与误差校正相结合的方法细化分性别死亡率发现， 男性及总体人群的死亡率分布在不同年龄段表现出高一致性； 女性死亡率则与总体死亡率呈线性关联， 进而以此构建各年龄段女性的死亡率与总体死亡率之间的回归模型，如式（２）～（５） 所示。其中， 自变量ｘａ～ｂ 为ａ ～ｂ 年龄段总人口死亡率， 因变量ｙ 为该年龄段女性人口死亡率。该模型通过了拟合效果验证（Ｒ２ ＝ ０. ９９６，Ｒ２ ＝０. ９６７， Ｒ２ ＝０. ９８１， Ｒ２ ＝０. ９８７）。

ｙ０～１４ ＝０. ９３８ｘ０～１４ ＋０. ０８８， Ｒ２ ＝０. ９９６ （２）

ｙ１５～４９ ＝１. ０２３ｘ１５～４９ ＋０. ３８９， Ｒ２ ＝０. ９６７ （３）

ｙ５０～６４ ＝１. １３４ｘ５０～６４ ＋１. ３０８， Ｒ２ ＝０. ９８１ （４）

ｙ６５＋ ＝１. ０６９ｘ６５＋ ＋２. ２４１， Ｒ２ ＝０. ９８７ （５）

２） 出生率预测

政策导向与经济活动共同影响人口出生率。本文引入政策虚拟变量建构多元回归分析模型， 为避免单一模型在整体数据拟合中的偏差， 通过分阶段回归， 其一般数学表达式如式（６） 所示：

出生率＝ε＋α１∗教育水平＋α２∗收入实际增长＋α３∗住宅价格＋β１∗独生政策＋β２ ∗二孩政策＋β３ ∗完全二孩政策（６）

从计划生育至二孩政策实施阶段， 多元回归结果如式（７） 所示：

出生率＝２６. ９１０－３. ０４８∗教育水平＋１１. ７１６∗独生政策＋１５. １９４∗二孩政策－０. １７５∗收入实际增长－０∗住宅价格（７）

完全二孩政策的实施标志政策的重大转变， 对出生率产生新的影响， 为解决变量之间的多重共线性， 采用岭回归重新进行参数估计后， 具体方程如式（８） 所示：

出生率＝３３. ７５７－１. ９８８∗教育水平－１. ３９４∗独生政策＋１. ３７９∗二孩政策＋１. ０７８∗完全二孩政策－０. １７９∗收入实际增长－０∗住宅价格（８）

其中， 各个政策变量按时间节点以虚拟变量０／１ 表示。教育水平以人均受教育年限衡量， 参考国家统计局的计算标准。收入实际增长与住宅价格均来源于国家统计局数据。经济、政策共同影响出生率， 从而影响人口变动。

回归结果显示， 两种模型均在统计学上意义显著， 通过多重共线性检验， 能够较好地拟合观测数据并预测人口出生率的变化趋势。值得注意的是，住宅售价平均值的变化并未对出生率有显著影响，在当前分析场景下， 房价波动对出生率的直接效应相对有限。

２. ５ 仿真有效性验证

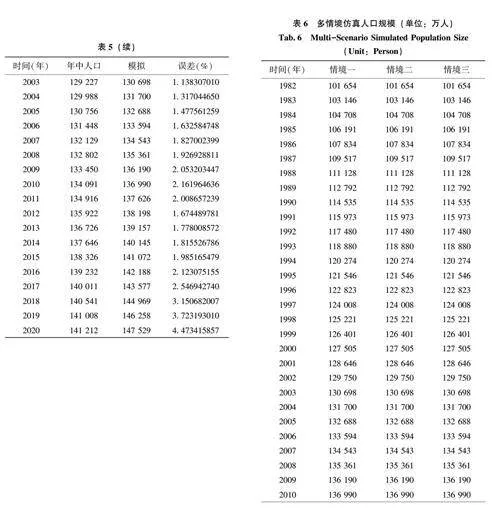
仿真结果可信度主要依赖参数稳健性， 主要通过比较真实数据与模型仿真数据的拟合精度及误差范围。依托Ｖｅｎｓｉｍ ＰＬＥ 平台进行仿真， 模拟时段设定为１９８２—２０２０ 年， 以每年为步长， 初始化数据源自１９８２ 年人口普查。由于真实死亡率数据的部分缺失， 考虑采用趋势外推法进行插补。总体而言， 趋势外推法在总死亡率预测上与历史数据吻合度较高， 人口总量预测误差始终维持在４. ５％以下，展现出良好的中期预测性能。

鉴于未成年人群死亡率的显著波动性， 对人口在年龄结构区间转变率进行调整。具体配置包括：１４ 岁人口占比分别为０. ０７２、０. ０７５、０. ０８０ 以探索最佳拟合， 同时， 为４９ 岁和６４ 岁人口设定了０. ０２０和０. ０５０ 的比值。结果显示， 当１４ 岁人口占比设定０. ０８０ 时， 仿真模型性能最佳， 预测误差降至最低，结果与历史数据发展趋势吻合， 最能反映人口在年龄结构区间流动的历史情况， 可作为模型预测的优先参数设定， 用于未来人口预测的参数设置依据。表５ 详列了上述最优参数设定下预测人口与实际人口的误差。

模型的有效性验证结果显示， 人口—经济—政策动力学仿真模型在中短期具有较高的准确度与可信度， 特别是在监测评估人口结构动态特性方面表现良好。

３ 人口生育政策多情景仿真比较分析

３. １ 仿真情境设计

以上述模型为基础， 研究模拟３ 种政策情景，以观察不同人口生育政策下人口规模与结构的趋势推演：１） 情境一： 模拟单一政策模型， 自１９８２ 年起始终保持严格的生育控制政策不变， 未有任何放松或调整；２） 情境二： 模拟两段政策模型， １９８２—２０１１年执行严格计划生育政策， 自２０１３ 年转向实施独生子女二孩政策， 并保持政策不变；３） 情境三： 模拟三段政策模型， 或真实政策仿真模型， 即１９８２—２０１２ 年实行严格计划生育政策， ２０１２—２０１５ 年实行二孩政策， ２０１６ 年起实行全面放开二孩政策。

３. ２ 仿真结果分析

３. ２. １ 人口规模分析

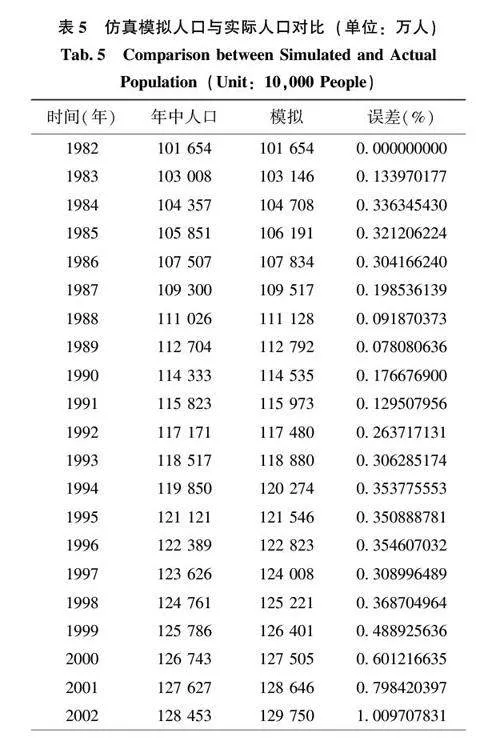
如表６ 所示， 人口规模仿真结果显示： 不同生育政策对我国２０２０—２０３０ 年人口规模存在差异化影响： ①在维持严格计划生育政策不变的假定下，人口增长轨迹平稳， １９８２—２０２０ 年的年均人口增长率约为０. ９％， ２０２０ 年以后增长率明显滑落， 约为０. ５％， 到２０３０ 年人口规模将缓慢扩张至约１５. ２亿； ②两段政策模型中， 人口增长曲线于２０１３ 年经历人口增长加速期， 预计年均增长率约为０. ８％，人口规模在２０３０ 年将突破１６ 亿； ③三段政策模型中， 完全二孩与二孩政策效果相近， 差异不显著，预示此调整对促进人口增长的成效甚微。具体动态变化对比图如图５ 所示。

总体而言， 尽管生育政策的调整在一定程度上能够促进人口增长， 但经济压力较大、育儿成本高昂、育龄妇女数量减少和社会观念变化等多重社会经济因素的制约， 限制了生育政策调整对人口增长的积极影响， 全面二孩政策实施后， 人口增幅未能达到预期效果。

３. ２. ２ 人口结构分析

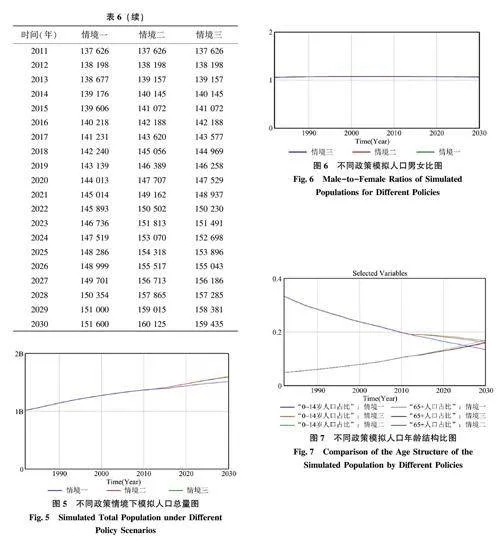
人口性别结构随政策的调整变动空间不大。图６展示了在不同政策调控场景下， 我国男女比例在预测期内基本维持在狭窄稳定的区间， 大约为１. ０６～１. ０７， 保持稳定。有研究关注到， 一孩性别对二孩政策的推行效果有微妙影响： 一孩为女孩的家庭，二孩生育意愿更强， 且期望男孩意愿更为强烈， 推动了男女比例的轻微上调。

图７ 展示年龄构成的差异性演化。严格计划生育政策下， ０～１４ 岁群体比例呈逐年递减趋势， 老龄人口比重攀升， 预示２０３０ 年少年与老年群体的比例分别为１４. ９２％、１６. ７９％， 老龄化挑战日益严峻。对比之下， 二段与三段生育政策的引入， 缓和了上述人口结构失衡问题， 虽取得一定成效， 但总体改善幅度有限。自１９８２ 年起， 少年儿童占总人口的比例从３３％大幅滑落， 预计２０３０ 年将进一步减少至约１７％。值得注意的是， 尽管政策有所调整，但６５ 岁及以上老年人口的比例依旧保持上升势头，预计将在２０３０ 年达到１６％的高度， 显示老龄化趋势的顽固性。两种调整政策场景下的差异相对微妙，人口结构的优化仍需更加精准和创新的策略干预。

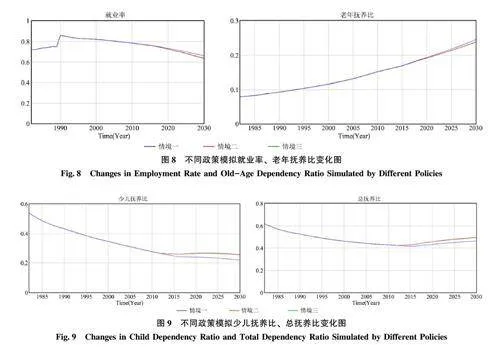
３. ２. ３ 监测指标分析

在相关指标监测中， 如图８、图９ 所示， 不同政策对就业率、老年抚养比的短期影响偏差不大，并未有显著性政策差异， 但少儿抚养比、总体抚养比显示出典型差异性。与计划生育相比， 独生子女二孩和全面二孩政策均显著提高了少儿抚养比， 间接减轻了老年抚养比， 缓解了社会保障压力和劳动人口的养老负担。然而， 两段政策模型与三段政策模型的抚养比曲线高度重叠， 全面二孩政策并未从根本上改变我国的抚养压力问题。

３. ３ 仿真结果小结

政策仿真模拟的结果显示， 我国现行生育政策调整对人口总量与年龄结构具有显著影响， 在缓解人口总和生育率下降与人口老龄化加速方面具有一定的预见性， 反映出单纯依赖人口生育政策宽松化的政策模式， 在就业压力较大、育儿成本快速增长的当前仍面临一定局限性， 高生育鼓励措施并不能完全实现政策预设的人口规模和结构调整目标。因此， 系统动力学仿真方法提供了一个综合性的策略分析框架， 可以逐步调整相关外部变量和因果关系，逐步探讨和预见强化育儿财政补助、实施更有力的生育鼓励政策、降低教育成本、改善医疗保健服务等政策对人口调控的影响， 拓展了人口生育政策分析的范畴和方法。

４ 结 语

依托系统动力学所构建的政策仿真模拟方法，能预估解析政策变动如何在复杂的社会生态系统内催生连锁效应。不仅反映政策干预的即时结果， 还追踪干预随时间积累的长远影响， 为决策层提供更长周期的分析视角， 增强政策应变能力和长期成效跟踪。

模拟结果显示， 生育政策调整虽对人口数量与结构有显著影响， 但单一政策效力有限， 单纯扁平化优化政策后的成效显著降低， 难以从根本上逆转低生育率和老龄化趋势。独生子女二孩政策之所以对我国人口产生较大影响， 其本质在于许多家庭的生育意愿得到了释放。长期以来， 渴望拥有二孩的家庭因政策限制而未能如愿， 新政策的出台给予了他们实现愿望的机会。然而， 全面放开二孩政策虽然能够在一定程度上释放被压抑的生育潜力， 但要大幅提高生育意愿却面临诸多挑战。在考虑育儿成本、教育开支以及生育风险等因素后， 很多家庭即便在政策允许的情况下， 也可能选择不再增加家庭成员。因此， 我国未来的生育政策不能仅限于生育婴孩数量本身， 更应该多方面进行调整， 如提高育儿补贴、奖励育儿、降低教育和育儿成本、改善医疗设备等， 利用经济和社会手段调整出生率， 从而改善人口结构。

面对人口结构转型的挑战， 生育政策不应仅仅停留在放宽限制的层面， 更应向一个更加全面、综合性的策略体系转变， 从单一激励生育转向多方位综合， 这一转变要求在教育投资增加、经济激励机制创新、养老服务体系完善等方面协同发力， 共同构建有利于人口均衡发展的社会环境。在此基础上，系统动力学仿真将继续作为强有力的分析工具， 为制定更加科学、高效的人口管理与社会发展政策提供坚实的数据支撑和理论依据。

系统动力学仿真作为一种分析工具， 也存在若干局限性。一是强相关性偏好与低因果解释， 模型更偏好相关性高的解释变量， 而高因果解释的变量可能在整体模型中无法通过检验， 因而无法用于模型的预测， 即“可用模型并不一定可解释”。二是无法判定模型的变量饱和性和最佳变量规模， 虽然借鉴了大量的已有模型， 但仍无法判定变量是否足够预测， 也无法判定单一变量对模型的贡献大小。对于超大规模变量的仿真模型， 模型有效性和效果显著性将会遇到挑战。此外， 在更大尺度的政策周期或不可预期的“黑天鹅” 事件， 如当前的经济周期和住房政策调整， 仍然无法在关联规则系统中有效预测。这些局限也是后续研究值得注意和改进的地方。

参考文献

［１］ 黄匡时． 计算人口学的学科范式、理论基础与技术方法［ Ｊ］．

北京工业大学学报（社会科学版）， ２０２１， ２１ （３）： １６－２７．

［２］ 马尔萨斯． 人口原理［ Ｍ］． 朱泱， 胡企林， 等译． 北京： 商

务印书馆， １９９２．

［３］ 冯玉祥． 中国人口问题［Ｍ］． 北京： 人民出版社， １９５３．

［４］ 于也雯， 龚六堂． 生育政策、生育率与家庭养老［Ｊ］． 中国工

业经济， ２０２１， （５）： ３８－５６．

［５］ 彭希哲， 胡湛． 公共政策视角下的中国人口老龄化［ Ｊ］． 中国

社会科学， ２０１１， （３）： １２１－１３８， ２２２－２２３．

［６］ 封进． 人口老龄化、社会保障及对劳动力市场的影响［ Ｊ］． 中

国经济问题， ２０１９， （５）： １５－３３．

［７］ 戴洛特， 郭宇春． 人口老龄化、社会保障支出与经济增长［Ｊ］．

统计理论与实践， ２０２４， （３）： ４０－４６．

［８］ 马子洋． “老龄化” “少子化” 叠加对居民消费的影响———基

于中国家庭追踪调查数据的实证［ Ｊ］． 商业经济研究， ２０２４，

（１２）： ６３－６７．

［９］ 张鹏飞， 苏畅． 人口老龄化、社会保障支出与财政负担［Ｊ］． 财

政研究， ２０１７， （１２）： ３３－４４．

［１０］ 郑录军， 韩庆潇． 生育政策、人口流动对宏观经济的影响［Ｊ］．

中国人口·资源与环境， ２０２２， ３２ （８）： １６３－１７３．

［１１］ 郑回静． 我国人口生育政策演变对住房需求的影响研究［Ｄ］．

上海： 上海社会科学院， ２０１８．

［１２］ 贾俊雪， 龙学文， 孙伟． 人口红利还是人力资本红利： 生育

政策经济影响的理论分析［ Ｊ］． 经济研究， ２０２１， ５６ （１２）：

１３０－１４８．

［１３］ 刘庆， 刘秀丽． 生育政策调整背景下２０１８—２１００ 年中国人口

规模与结构预测研究［Ｊ］． 数学的实践与认识， ２０１８， ４８ （８）：

１８０－１８８．

［１４］ 李勇， 孙琪． 如何有效促进人口生育水平提升———基于江苏

省人口出生率影响因素的实证分析［Ｊ］． 中国卫生事业管理，

２０２３， ４０ （７）： ４８６－４９０．

［１５］ 汪伟． 人口老龄化、生育政策调整与中国经济增长［ Ｊ］． 经

济学（季刊）， ２０１７， １６ （１）： ６７－９６．

［１６］ 王金营． 中国计划生育政策的人口效果评估［ Ｊ］． 中国人口

科学， ２００６， （５）： ２３－３２， ９５．

［１７］ 王国军， 赵小静， 周新发． 我国人口出生率影响因素实证研

究———基于计划生育政策、社会保障视角［Ｊ］． 经济问题， ２０１６，

（２）： ７－１１．

［１８］ 潘金洪， 胡创奇， 郝仁杰． 生育政策调整带来的生育率变化对

人口老龄化的影响———以江苏省为例［Ｊ］． 人口与社会， ２０１８，

３４ （５）： ３－１７．

［１９］ Ｔｕｃｋｅｒ Ｃ， Ｈｏｏｋ Ｊ． Ｓｕｒｐｌｕｓ Ｃｈｉｎｅｓｅ Ｍｅｎ： Ｄｅｍｏｇｒａｐｈｉｃ Ｄｅｔｅｒｍｉ⁃

ｎａｎｔｓ ｏｆ ｔｈｅ Ｓｅｘ Ｒａｔｉｏ ａｔ Ｍａｒｒｉａｇｅａｂｌｅ Ａｇｅｓ ｉｎ Ｃｈｉｎａ ［Ｊ］． Ｐｏｐｕｌａ⁃

ｔｉｏｎ ａｎｄ Ｄｅｖｅｌｏｐｍｅｎｔ Ｒｅｖｉｅｗ， ２０１３， ３９ （２）： ２０９－２２９．

［２０］ 汤兆云． 生育政策对出生性别比升高影响及未来生育政策的

走向［Ｊ］． 江苏社会科学， ２０１１， （６）： ５５－６０．

［２１］ 盛亦男． 生育政策调整对女性就业质量的影响［ Ｊ］． 人口与

经济， ２０１９， （３）： ６２－７６．

［２２］ 李松臣， 张世英． 基于逐步回归法的人口出生率影响因素分

析［Ｊ］． 统计与决策， ２００８， （４）： ７－９．

［２３］ 玛依拉·吐尔逊， 常轩． 我国人口出生率及其影响因素研究———

基于动态ＧＭＭ 模型和门限模型的实证分析［Ｊ］． 价格理论与实

践， ２０１９， （１１）： ５３－５６．

［２４］ 甘舟颖． 二孩政策背景下城市新移民的生育保障制度探析

［Ｊ］． 中外企业家， ２０１８， （２４）： ２０１－２０２．（

［２５］ Ｆｏｒｒｅｓｔｅｒ Ｊ Ｗ． Ｉｎｄｕｓｔｒｉａｌ Ｄｙｎａｍｉｃｓ： Ａ Ｍａｊｏｒ Ｂｒｅａｋｔｈｒｏｕｇｈ ｆｏｒ Ｄｅｃｉ⁃

ｓｉｏｎ Ｍａｋｅｒｓ ［Ｊ］． Ｈａｒｖａｒｄ Ｂｕｓｉｎｅｓｓ Ｒｅｖｉｅｗ， １９５８， ３６ （４）： ３７－６６．

［２６］ 许光清， 邹骥． 系统动力学方法： 原理、特点与最新进展［Ｊ］．

哈尔滨工业大学学报（社会科学版）， ２００６， （４）： ７２－７７．

［２７］ 张一文， 齐佳音， 马君， 等． 网络舆情与非常规突发事件作

用机制———基于系统动力学建模分析［Ｊ］． 情报杂志， ２０１０， ２９

（９）： １－６．

［２８］ Ｓａｅｅｄ Ｋ． Ｔｈｅ Ｄｙｎａｍｉｃｓ ｏｆ Ｅｃｏｎｏｍｉｃ Ｇｒｏｗｔｈ ａｎｄ Ｐｏｌｉｔｉｃａｌ Ｉｎｓｔａ⁃

ｂｉｌｉｔｙ ｉｎ Ｄｅｖｅｌｏｐｉｎｇ Ｃｏｕｎｔｒｉｅｓ ［Ｊ］． Ｓｙｓｔｅｍ Ｄｙｎａｍｉｃｓ Ｒｅｖｉｅｗ， １９８６， ２

（１）： ２０－３５．

［２９］ 刘耀彬， 陈斐， 李仁东． 区域城市化与生态环境耦合发展模拟

及调控策略———以江苏省为例［Ｊ］． 地理研究， ２００７， （１）： １８７－

１９６．

［３０］ 张友棠， 黄阳． 基于行业环境风险识别的企业财务预警控制

系统研究［Ｊ］． 会计研究， ２０１１， （３）： ４１－４８， ９５．

［３１］ 李旭． 社会系统动力学： 政策研究的原理、方法和应用［Ｍ］．

上海： 复旦大学出版社， ２００９．

［３２］ Ｐｉｔｏｙｏ Ａ Ｊ， Ｕｌｈａｑ Ｍ Ｄ， Ｗａｈｉｄ Ａ， ｅｔ ａｌ． Ｓｙｓｔｅｍ Ｄｙｎａｍｉｃｓ

Ｍｏｄｅｌｉｎｇ ｏｆ Ｉｎｄｏｎｅｓｉａ Ｐｏｐｕｌａｔｉｏｎ Ｐｒｏｊｅｃｔｉｏｎ Ｍｏｄｅｌ ［Ｊ］． ＩＯＰ Ｃｏｎｆｅｒ⁃

ｅｎｃｅ Ｓｅｒｉｅｓ： Ｅａｒｔｈ ａｎｄ Ｅｎｖｉｒｏｎｍｅｎｔａｌ Ｓｃｉｅｎｃｅ， ２０１８， １４５： ０１２１１７．

［３３］ 赵景柱． 人口与社会—经济—自然复合生态系统的持续发展———

伊春市人口的系统分析与调控对策［Ｊ］． 生态学报， １９９２， （１）：

７７－８３．

［３４］ 李旭． 社会系统动力学： 政策研究的原理、方法和应用［Ｍ］．

上海： 复旦大学出版社， ２００９．

［３５］ 李香霞． 基于系统动力学的江苏省人口预测仿真研究［Ｊ］． 管

理观察， ２０１９， （９）： ７６－７８．

［３６］ 朱墨蕤， 严明义． 人口老龄化与财政支出结构———基于中国经

验的ＳＤ 分析［Ｊ］． 统计与信息论坛， ２０１９， ３４ （１１）： ５０－５８．

［３７］ 刘靖， 张岩， 李娜． 区域经济转型与教育因果反馈及仿真模

拟———以长三角为例［Ｊ］． 经济问题探索， ２０１５， （１０）： ８２－８８．

［３８］ 吴信如， 王静， 王文婷． 中国人口政策的经济效应： ＯＬＧ 模

型和Ｐａｎｅｌ 数据分析［ Ｊ］． 华东师范大学学报（ 哲学社会科学

版）， ２０１５， ４７ （４）： ９３－９９， １７０．

［３９］ 王维国， 刘丰， 胡春龙． 生育政策、人口年龄结构优化与经

济增长［Ｊ］． 经济研究， ２０１９， ５４ （１）： １１６－１３１．

［４０］ 瞿凌云． 人口政策的经济效应分析———基于人口数量与质量

替代效应的视角［Ｊ］． 人口与经济， ２０１３， （５）： ２４－３２．

［４１］ Ｌｅｅ Ｒ Ｄ， Ｃａｒｔｅｒ Ｌ Ｒ． Ｍｏｄｅｌｉｎｇ ａｎｄ Ｆｏｒｅｃａｓｔｉｎｇ Ｕ Ｓ． Ｍｏｒｔａｌｉｔｙ ［Ｊ］．

Ｊｏｕｒｎａｌ ｏｆ ｔｈｅ Ａｍｅｒｉｃａｎ Ｓｔａｔｉｓｔｉｃａｌ Ａｓｓｏｃｉａｔｉｏｎ， １９９２， ８７ （ ４１９）：６５９．

（责任编辑： 郭沫含）