数控机床旋转轴多自由度静/热误差同步测量与建模

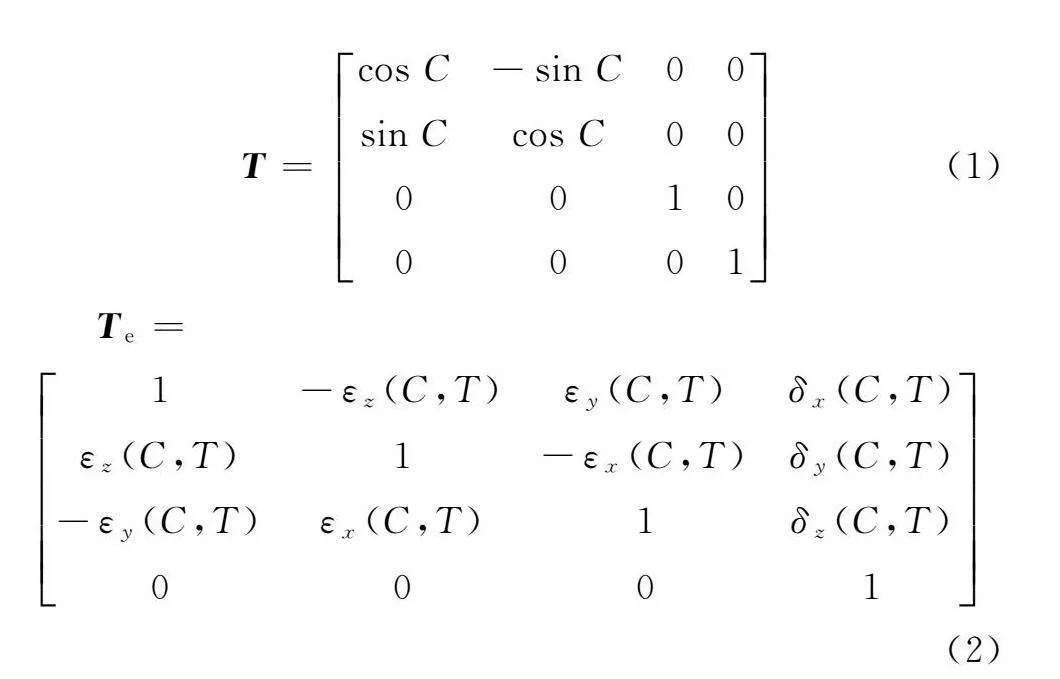
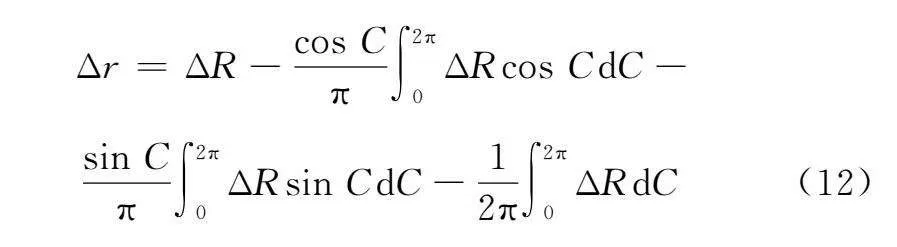
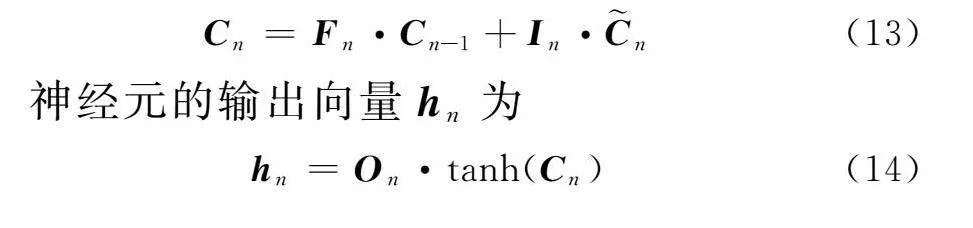
摘要：针对现有的数控机床旋转轴误差测量与建模方法仅考虑多自由度静态几何误差或单自由度热误差单独作用的影响，未考虑几何误差和热误差耦合影响的问题，提出了一种基于球杆仪的数控机床旋转轴多自由度静/热误差同步测量与建模方法。首先基于齐次坐标变换建立球杆仪杆长变化模型，再基于该模型使用非齐次线性方程组建立静/热误差辨识模型;其次设计了适应多自由度静/热误差同步测量的球杆仪安装模式以缩短测量时间，减少热逸散对测量结果的影响;再次基于卷积长短期记忆神经网络（CNN-LSTM）建立旋转轴多自由度静/热误差预测模型;最后在数控蜗杆砂轮磨齿机的C轴上进行误差测量实验，对多种转速下的旋转轴多自由度误差进行快速辨识，并通过CNN-LSTM静/热误差预测模型对多自由度误差和球杆仪杆长变化进行预测，以验证所建模型的准确性。

关键词：静/热误差；误差测量；卷积长短期记忆神经网络；旋转轴；球杆仪

中图分类号：TH161

DOI：10.3969/j.issn.1004132X.2024.08.011

开放科学（资源服务）标识码（OSID）：

Simultaneous Measurement and Modeling of MDOF Static/Thermal Errors

of CNC Machine Tool Rotational Axes

LI Guolong1 XIAO Yang1 LI Zheyu1 XU Kai2 ZHANG Wei1

1.State Key Laboratory of Mechanical Transmission，Chongqing University，Chongqing，400044

2.School of Mechanical Engineering，Chongqing University of Technology，Chongqing，400054

Abstract： Existing measurement and modeling methods for CNC machine tool rotational axis errors only considered the influences of multiple degrees of freedom（MDOF） static geometric errors or single degree of freedom thermal errors acting in isolation without accounting for the coupled effects， a simultaneous measurement and modeling for MDOF static/thermal errors in CNC machine tool rotational axes was proposed based on a double ball bar. Firstly， a model was developed to describe the variation in length of the double ball bar using homogeneous coordinate transformation. A static/thermal error identification model was constructed by solving a system of nonhomogeneous linear equations based on this model. Subsequently， to minimize the influences of thermal dissipation on the measurement results， a specific installation mode adapted to the simultaneous measurement of MDOF static/thermal errors was designed to reduce the installation time of the double ball bar. Additionally， a prediction model for MDOF static/thermal errors in rotational axis was established using a CNN-LSTM. Finally， experiments were conducted on the C-axis of a gear grinding machine to rapidly identify the rotational axis errors at various speeds. The accuracy of the prediction model was verified by utilizing the static/thermal error model to predict the errors of C-axis and the variation in length of the double ball bar.

Key words：static/thermal error; error measurement; convolutional neural network long-short-term memory（CNN-LSTM）; rotating axis; double ball bar

0 引言

数控机床在运行过程中受到几何误差、热误差、力误差、控制误差等多种误差的共同影响，导致数控机床刀具与工件的相对位姿发生改变，产生加工误差。其中，几何误差与热误差是最主要的误差源，占机床总误差的80%以上［1-3］。随着五轴加工需求的不断增加，旋转轴的误差对工件加工精度的影响也越来越大，对数控机床旋转轴误差进行测量、建模、补偿是减小加工误差的有效方法。

几何误差是标准测试环境、无负载下的静态误差［4］。根据国际标准［5］，旋转轴的几何误差按位置和误差的关联性分为位置相关几何误差（position dependent geometric errors，PDGEs）和位置无关几何误差（position independent geometric errors，PIGEs）。球杆仪操作简单，成本相对较低，常用于测量数控机床静态几何误差［6-7］。LI等［8］通过球杆仪的4个不同安装位置的8种测量模式能够测量出旋转轴所有的12个位置相关误差，该方法测量精准但测量模式多，安装较为复杂。徐凯等［9］利用球杆仪提出了一种基于参数化建模的旋转轴PDGEs快速辨识方法，该方法便捷快速，可直接用于旋转轴及机床误差的建模及补偿过程。ZARGARBASHI等［10］提出了一种只需安装一次球杆仪便能测量A轴轴向运动误差的方法，但是只能使用于特定机床。梁小冰等［11］通过现有的辨识方法获得旋转轴PIGEs初始解，然后定义优化目标函数，通过差分演化算法整体优化求解旋转轴PIGEs，提高了辨识准确性。FU等［12］提出了一种基于差动矩阵的球杆仪六圈法，能够对旋转轴的4项PIGEs和6项PDGEs进行测量和辨识。郭世杰等［13］为实现几何误差精准建模，提出了基于遗传算法量子粒子群算法（genetic algorithm quantum-behaved particle swarm optimization， GA-QPSO）的正弦低次多项式参数化建模方法，补偿后误差指标平均能够降低61.2%。但上述方法均只针对静态几何误差进行测量和建模，并未考虑机床长时间运行过程中的温度变化对这些误差元素的影响。

热误差是温度变化导致数控机床各零部件热变形而产生的误差，其本身具有动态、非线性特点，误差预测模型较为复杂［14］。目前，机床旋转轴的热误差主要借鉴ISO230-3中的五点法［15］，测量旋转轴旋转中心在特定方向上的动态变化。魏弦［16］基于五点法对磨齿机工件主轴（C轴）进行了测量，并提出了工件主轴无温度传感器分类建模方法，利用在线数据对模型进行修正，提高了模型的自适应性能。何振亚等［17］基于球杆仪提出了主轴热误差检测新方法，该方法借助五轴数控机床的两个旋转轴分别单独运动，实现两个正交圆或圆弧构成的球杆仪空间轨迹测量，测量结果与五点法吻合。WU等［18］使用激光干涉仪测量误差数据，建立的卷积神经网络（convolutional neural network，CNN）模型能够精确地预测旋转轴热角度定位误差。上述方法虽然提出了热误差测量和建模方法，但均只针对某一方向上的误差的综合表现，未考虑具体的各个自由度上的误差元素。

针对目前的研究大多只考虑多自由度静态几何误差或单一自由度热误差单独作用的影响，并未考虑多自由度静/热误差影响（即静态几何误差和多自由度热误差耦合对旋转轴的影响）的问题，本文提出了一种基于球杆仪的旋转轴多自由度静/热误差同步测量与建模方法。建立基于球杆仪杆长变化的多自由度空间误差辨识模型，再通过设计特定的安装模式，对旋转轴多自由度静/热误差进行同步测量，并建立基于卷积长短期记忆神经网络（convolutional neural network-long short-term memory，CNN-LSTM）的旋转轴静/热误差预测模型。

1 基于球杆仪的多自由度空间误差建模

1.1 球杆仪杆长变化模型

考虑热误差对旋转轴位置相关误差的影响，提出位置相关热误差（position dependent thermal errors， PDTEs）和位置无关热误差（position independent thermal errors， PITEs），本文针对研究对象多自由度静/热误差采用PDGEs和PDTEs的定义。如图1所示，转动副绕旋转轴转动时存在6项误差元素［19-20］，包括3项移动误差δx（C，T）、δy（C，T）、δz（C，T）和3项角度误差εx（C，T）、εy（C，T）、εz（C，T）。其中，δx（C，T）、δy（C，T）、δz（C，T）分别为C轴沿X轴、Y轴、Z轴坐标方向的移动误差，εx（C，T）、εy（C，T）、εz（C，T）分别为C轴绕X轴、Y轴、Z轴旋转的角度误差。

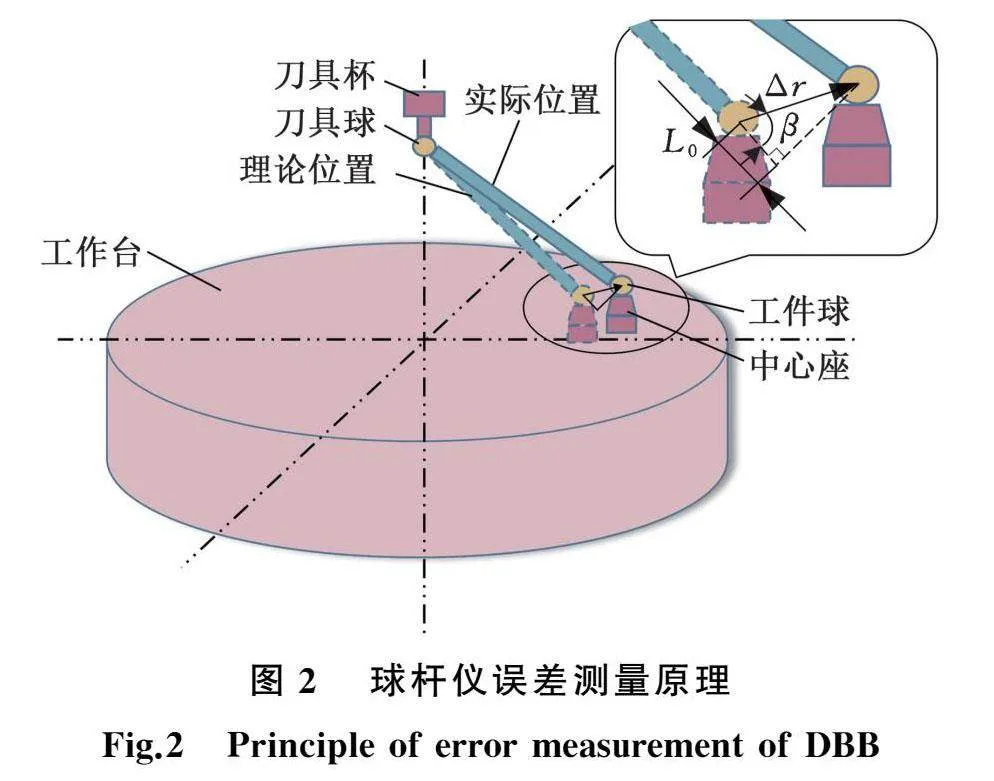
球杆仪由两个精密小球及直线位移传感器组成，使用时安装在工作台上的小球称为工件球，安装在主轴端的小球称为刀具球，如图2所示。设工件球坐标为P=（x0，y0，z0，1）T，刀具球坐标为Q=（0，0，h，1）T，h为刀具球起始安装位置的高度。在旋转轴单轴驱动模型下不考虑数控机床其他轴的运动，当旋转轴转过角度C时，其理想坐标变换矩阵为T，坐标变换误差矩阵为Te，即

T=cos C-sin C00

sin Ccos C00

0010

0001（1）

Te=

1－εz（C，T）εy（C，T）δx（C，T）εz（C，T）1－εx（C，T）δy（C，T）－εy（C，T）εx（C，T）1δz（C，T）0001（2）

工件球理论位置坐标Pi=（x′，y′，z′，1）T和实际位置坐标Pe=（x1，y1，z1，1）T计算公式为

Pi=TP

Pe=TeTP（3）

工件球空间误差矩阵Δr为工件球实际位置坐标与理论位置坐标的差：

Δr=TeTP－TP=（Δx，Δy，Δz，0）T（4）

Δx=－x0εz（C，T）sin C－y0εz（C，T）cos C+

z0εy（C，T）+δx（C，T）

Δy=x0εz（C，T）cos C－y0εz（C，T）sin C－

z0εx（C，T）+δy（C，T）

Δz=（εx（C，T）sin C－εy（C，T）cos C）x0+

（εy（C，T）sin C+εx（C，T）cos C）y0+δz（C，T）（5）

其中，Δx、Δy、Δz分别为X轴、Y轴和Z轴上的误差分量。分离6项误差元素：

e=（δx（C，T），δy（C，T），δz（C，T），εx（C，T），

εy（C，T），εz（C，T））T

则分离后的Δr可表示为

Δr=Tne=

1000z0－a010－z00b001a－b0000000δx（C，T）δy（C，T）δz（C，T）εx（C，T）εy（C，T）εz（C，T）（6）

a=x0sin C+y0cos C

b=x0cos C－y0sin C（7）

如图2所示，设β为误差向量与球杆仪理论位置之间的夹角，当β趋于无穷小时，球杆仪初始长度L0=Δrcos β≈ΔL0。可得到球杆仪长度变化量ΔL0与旋转轴各项误差之间的关系：

ΔL0=（n·Δr）=1L0baz0－h0T

Δr=1L0baz0－h－ahbh0Tδx（C，T）δy（C，T）δz（C，T）εx（C，T）εy（C，T）εz（C，T）（8）

式中，n为球杆仪理论位置的单位方向。

由式（8）可知，C轴绕Z轴的角度误差εz（C， T）在计算过程中与0相乘被抵消掉，故无法被辨识。则可得到在安装参数P、Q影响下的球杆仪杆长变化模型：

L0ΔL=bδx（C，T）+aδy（C，T）+（z0－h）δz（C，T）－

ahεx（C，T）+bhεy（C，T）（9）

1.2 多自由度空间误差辨识模型

球杆仪杆长的变化对应5项误差的变化，而每一次单独的球杆仪杆长测量实验都对应多个误差分量。当进行5次线性无关的球杆仪测量实验时就能求解出Δr：

（b1δx（C，T）+a1δy（C，T）+（z1－h）δz（C，T）－

a1h1εx（C，T）+b1h1εy（C，T））=L1ΔL1

（b5δx（C，T）+a5δy（C，T）+（z5－h）δz（C，T）－

a5h5εx（C，T）+b5h5εy（C，T））=L5ΔL5（10）

LiΔL=ΔTer=

b1a1z1－h1－ah1bh1b2a2z2－h2－ah2bh2b3a3z3－h3－ah3bh3b4a4z4－h4－ah4bh4b5a5z5－h5－ah5bh5·

δx（C，T）δy（C，T）δz（C，T）εx（C，T）εy（C，T）=LiΔL1ΔL2ΔL3ΔL4ΔL5（11）

Li=diag（L1，L2，…，L5）

实际上，Li为常量，求解式（11）就是求解非齐次线性方程组，当误差辨识矩阵ΔT满秩即r（ΔT）=5时，可求解出er=（δx（C，T），δy（C，T），δz（C，T），εx（C，T），εy（C，T））中的5项误差元素。当r（ΔT）lt;5时，方程组有无穷多解；当r（ΔT）gt;5时，方程组无解。所以设计测量模式时应该满足误差辨识矩阵满秩条件。

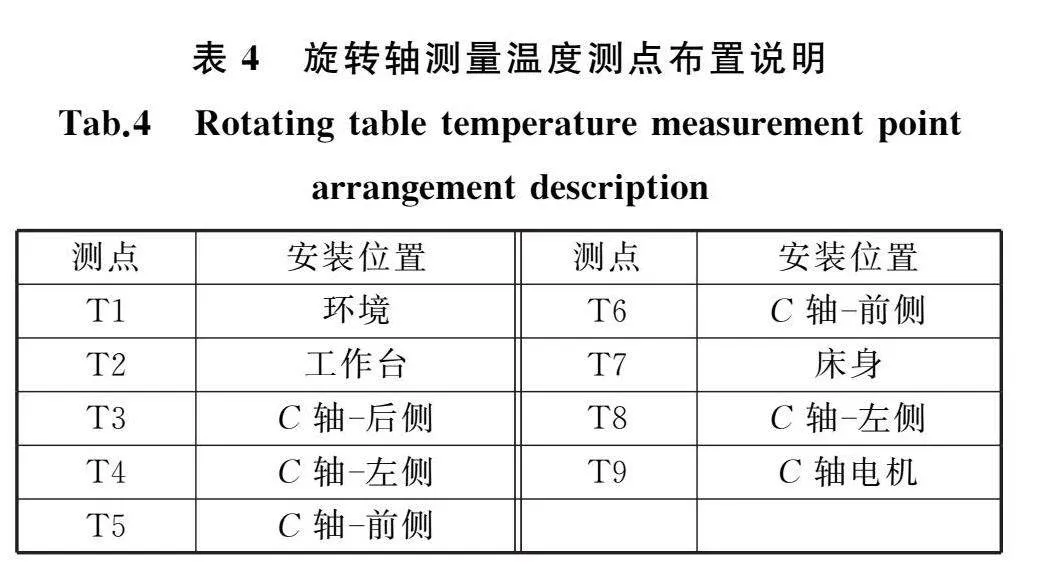
此外，球杆仪安装过程中存在人为安装导致的安装误差，基于笔者课题组前期的研究［9］进行安装误差消除，可消除球杆仪变化中由PIGEs和安装误差引起的影响，得到仅由PDGEs引起的球杆仪杆长变化Δr：

Δr=ΔR－cos Cπ∫2π0ΔRcos CdC－

sin Cπ∫2π0ΔRsin CdC－12π∫2π0ΔRdC（12）

2 多自由度静/热误差同步测量与建模

2.1 多自由度静/热误差同步测量方案

要满足数控机床旋转轴静/热误差的同步测量，设计球杆仪误差测量方案时应考虑两个问题：一是误差辨识矩阵需要满秩，以保证误差辨识模型有解，能够辨识出5项空间误差；二是不同测量模式之间需要更换迅速、测量方便，以降低球杆仪测量过程中的温度变化对测量结果的影响，保证多自由度热误差测量的准确性。

值得注意的是，为满足误差辨识矩阵满秩条件，可以选择的安装方式有很多，但是同时考虑到误差测量过程中热量逸散对热误差数据的影响，所以安装方式的选择应该方便、快捷。安装位置的设计应满足以下要求：①球杆仪不需要频繁拆解，即球杆仪长度保持一致；②球杆仪安装次数尽量少，即中心座位置变动少；③运动过程中不能发生干涉。

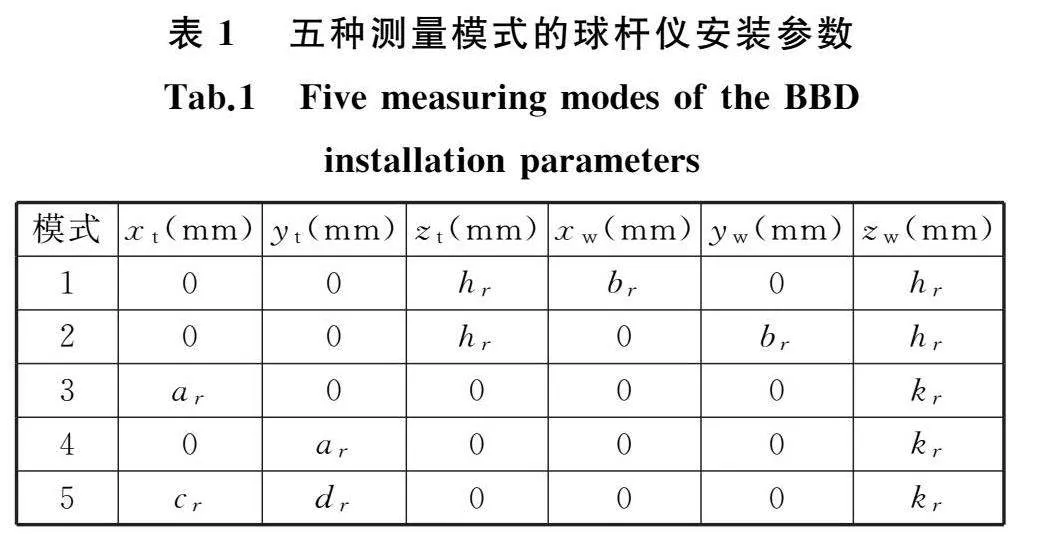
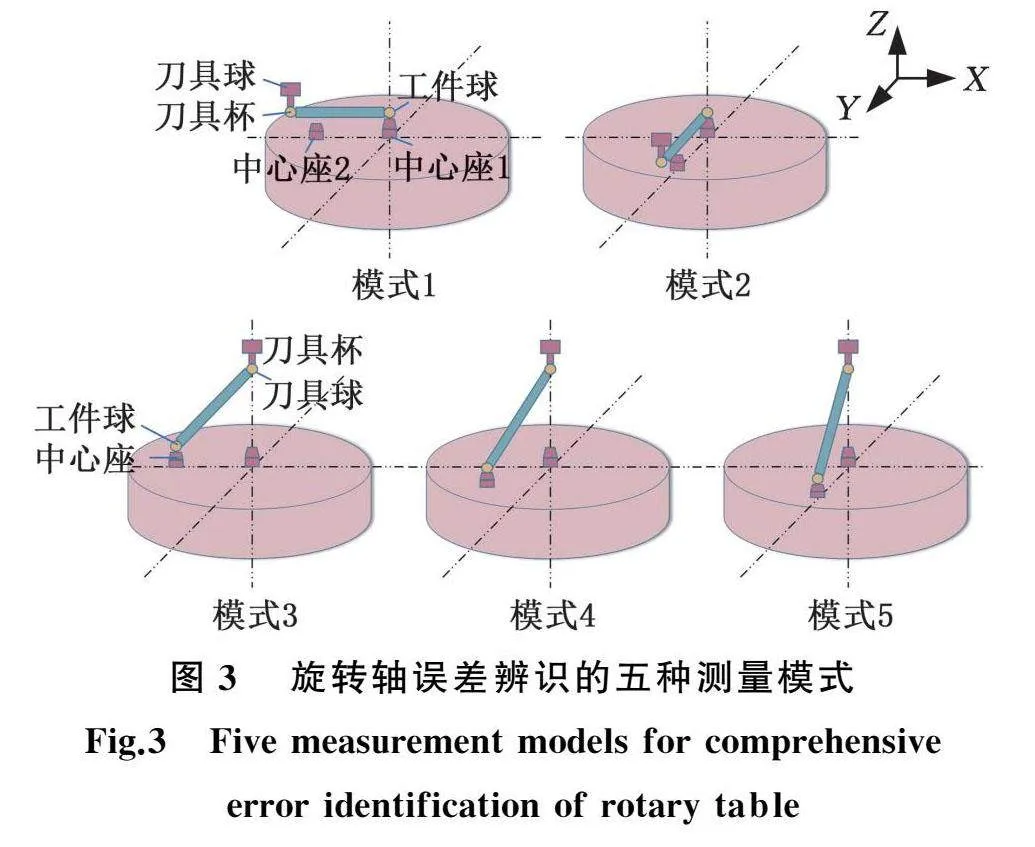
本文设计使用的5种球杆仪测量模式如图3所示，具体安装参数见表1。表1中，xt、yt、zt代表工件球起始坐标位置，xw、yw、zw代表刀具球起始坐标位置。以中心座1位置作为XY平面坐标原点，以中心座2的高度作为Z轴坐标原点。安装模式1、2的中心座1安装在旋转轴轴心，高度为hr；刀具杯1安装在与中心座1同一高度且距离旋转轴轴心br处坐标轴上。安装模式3、4、5的中心座2安装在距离旋转轴轴心ar的工作台上；刀具杯2安装在中心座1上方，高度为kr。hr、br、ar、kr、cr、dr为特定安装模式下刀具球或工件球起始安装位置的具体坐标值。

图3中，开始测量对刀时就提前安装好安装模式1、2和安装模式3、4、5的中心座。为减少球杆仪拆卸次数，令（a2r+k2r）1/2=br以保证球杆仪长度始终保持不变；为减少球杆仪安装次数和中心座位置变动，令（c2r+d2r）1/2=ar以保证中心座到旋转轴中心距离保持不变；为避免运动过程中发生干涉，以中心座2的高度为Z轴原点，中心座1的高度为XY平面原点，即可避免相撞。该测量方案通过简单地控制工作台旋转和刀具运动就能调整工件球和刀具球坐标，实现各种安装模式之间的快速切换。

此安装方案满足误差辨识矩阵满秩，工件球安装方便，不用频繁拆装，缩短了测量和安装时间，能够大幅提高误差测量的准确性。这种测量方案既能满足旋转轴静态误差的测量，也适用于旋转轴在工作一段时间后的静/热误差的同步测量。

2.2 基于CNN-LSTM的旋转轴静/热误差模型

基于上述误差辨识模型与误差测量方案，可以得到不同温度与位置下的误差值，进一步可以构建旋转轴静/热误差的预测模型。热误差建模方法包括多元回归法、神经网络法、灰色理论法、支持向量机等［21-23］方法。其中，神经网络因具有大规模的并行分式计算、计算能力强、容错率高、鲁棒性强等特点而得到广泛的应用。卷积神经网络是一种前馈神经网络，能在数据中提取有效的特征［24］。长短时记忆神经网络（long short-term memory， LSTM）［25］是在循环神经网络（recurrent neural network，RNN）的基础上发展而来的，用于解决RNN中的梯度消失问题，同时也解决了复杂长时间滞后的问题，而机床热误差的变化相对温度变化具有时间滞后效应，所以近年来LSTM模型常用于热误差建模［26］。

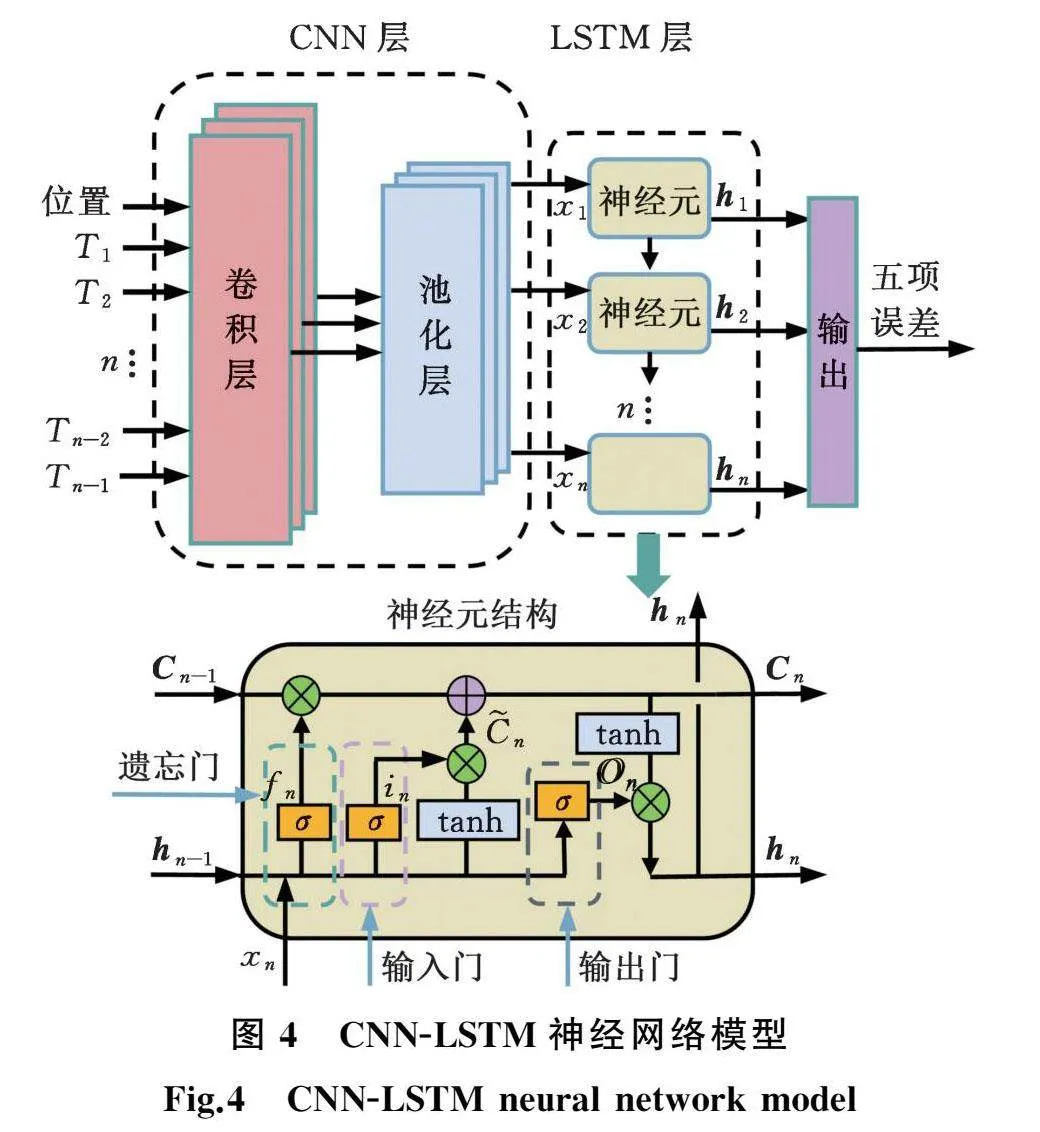
CNN-LSTM模型［27］结合了上述两种网络模型的优点，具有强大的特征提取能力和记忆能力，因此，本文采用CNN-LSTM模型进行建模，其神经网络结构如图4所示。CNN的卷积层对数据特征信息（温度、位置）进行提取；通过池化层降低特征信息维度，并保留重要的特征信息；将池化后的特征信息转换为一维向量输入LSTM层进行时序信息建模；输出最终的预测结果。

LSTM神经元由输入门、遗忘门、输出门三个门控结构构成，遗忘门用于控制当前输入数据的重要性，输出结果为fn；输入门用于控制过去时刻的记忆在当前时刻的重要性，输出结果为in；输出门用于控制当前时刻的输出，输出结果为On。计算流程如下：n时刻的输入向量xn和n-1时刻的输出向量hn-1进入神经元的遗忘门、输入门和输出门中。遗忘门的计算结果fn控制存储信息Cn-1中的哪些信息会被遗忘，输入门的计算结果it控制新信息中的哪一部分会被存储进Cn中，输出门的计算结果On控制Cn中的哪些信息会被当作hn输出。最后输出hn并将hn和Cn传给下一时刻的神经元。记忆单元存储信息Cn的更新公式如下：

Cn=Fn·Cn－1+In·n（13）

神经元的输出向量hn为

hn=On·tanh（Cn）（14）

3 实验与验证

3.1 误差测量实验

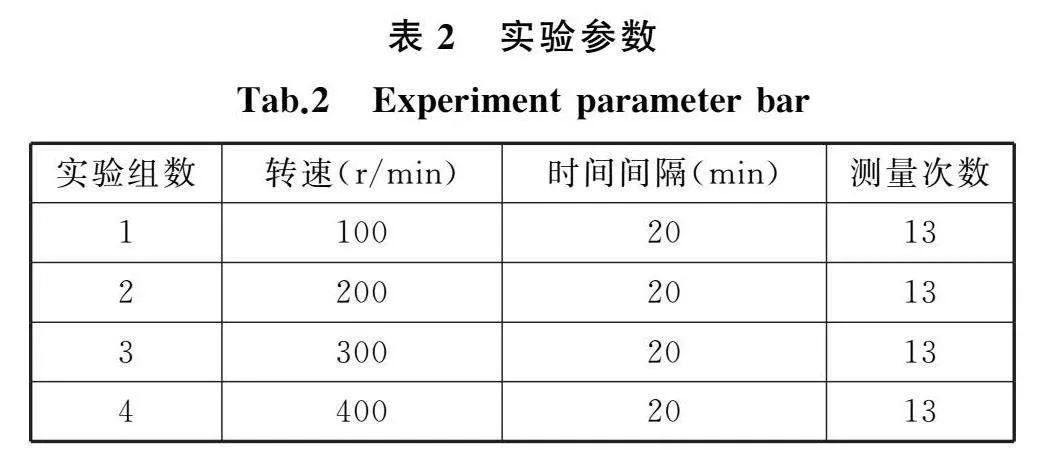
为测得旋转轴多自由度静/热误差，设计了四组实验。四组实验以转速为变量，分别反映了旋转轴在不同工况下产生的误差，随着工作时间的增加，模拟不同温度对误差的影响。实验过程中以机床温度20 ℃、工作台起始位置0°为边界条件，如图5中模式1所示。让工作台在固定的转速下持续工作4 h，从工作台静态开始每间隔工作20 min便使用球杆仪按照误差辨识模型的5种安装模式分别进行杆长变化测量，测量过程如图5所示，具体实验参数见表2，共测得260组数据，同时采集旋转轴的各项温度数据，建立静/热误差关系。

本文以YS7232机床C轴为研究对象，进行旋转轴静/热误差测量。球杆仪、温度采集卡和温度传感器参数见表3，传感器的位置布置如图6所示，具体位置见表4。其中，温度测点T1和T7分别测量环境温度和机床床身温度，其他温度传感器采集C轴附近温度，T9为直接读取的电机温度。

3.2 实验结果

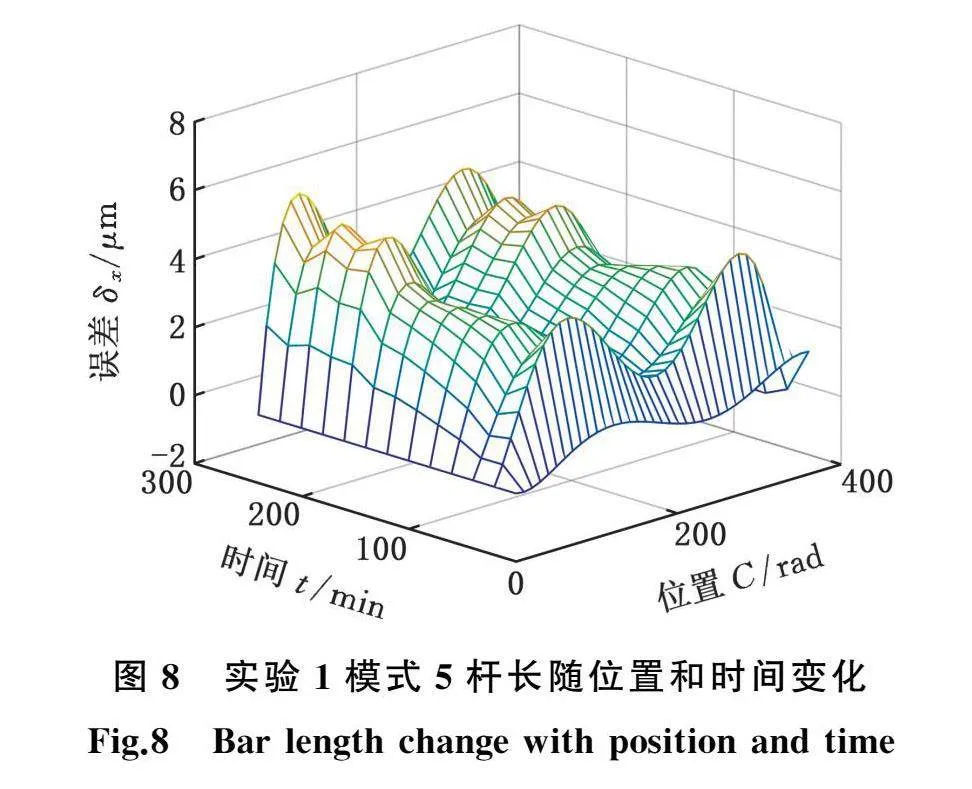
以转速为300 r/min的试验结果为例，温度变化和消除安装误差后的实验1模式5的杆长随位置和时间的变化结果如图7、图8所示。为方便观察变化量，本文都取相对变化值。随着工作台工作时间的增加，温度不断上升。其中，C轴电机的温度上升最剧烈，温升超过7 ℃；床身和环境温度变化趋势比较平缓，在1 ℃以内；C轴和工作台各测点温度上升相对一致，在3～4 ℃。杆长变化量随位置变化呈三角函数型波动，杆长变化幅值随着时间的变化也逐渐变大。

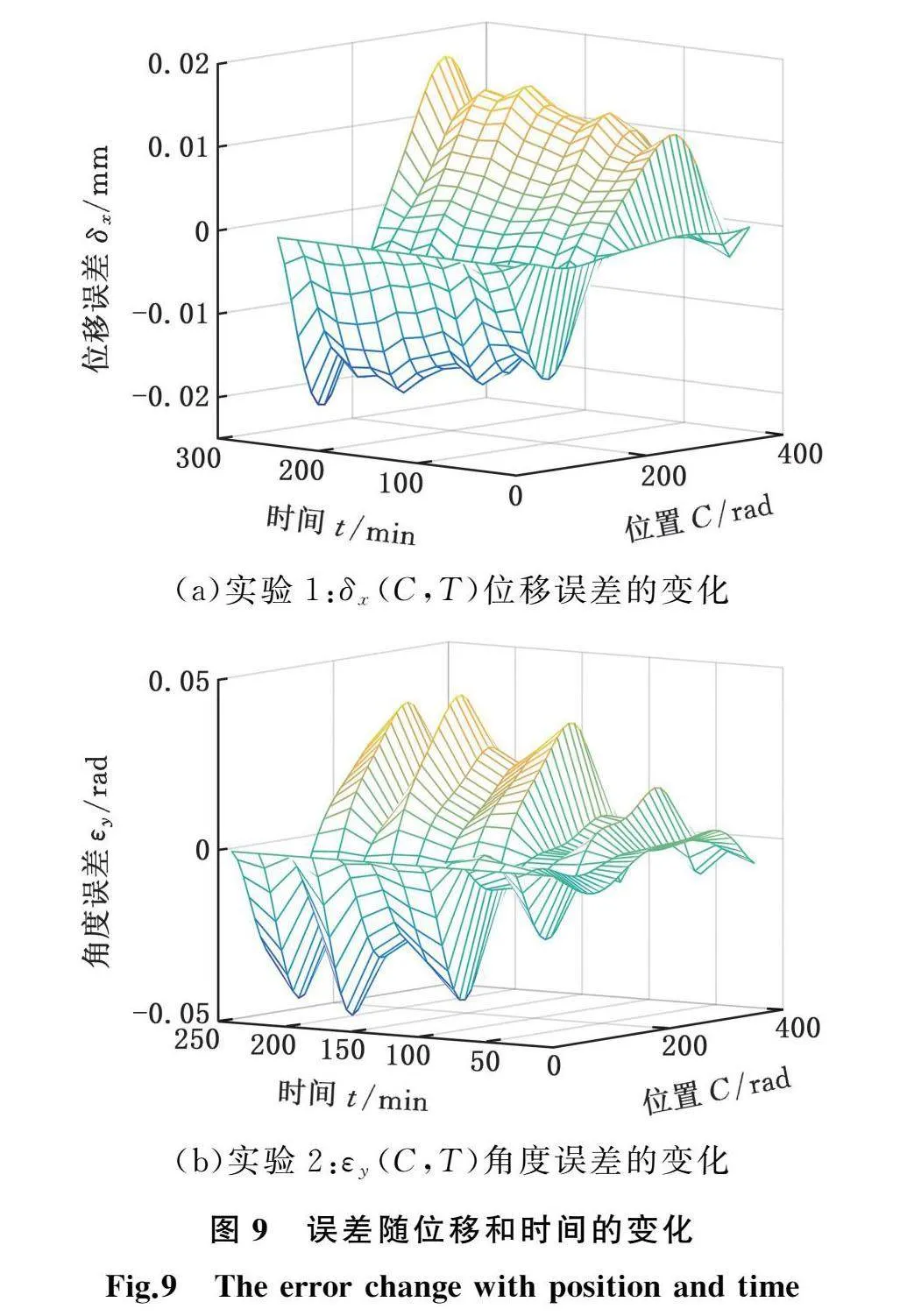
将5种安装模式下的杆长变化代入误差辨识模型即可辨识得到五项误差数据，为同时表达误差与运动位置和时间的关系，建立三维图对误差进行描述，实验1的δx（C，T）（第一组实验的机床X向移动误差，后同）和实验2的εy（C，T）如图9所示。其中，X轴位置数据表示球杆仪旋转角度映射位置的相关误差，Y轴表示旋转轴工作时间来反映温度的变化对热误差的影响，Z轴表示辨识出的误差值。时间为0时为静态误差，随着工作时间的增加，热误差产生影响，误差变化的幅值也逐渐增大；随着工作台的旋转，误差在X轴上呈类三角函数分布。因篇幅所限，其他组数据不再赘述。

3.3 误差预测

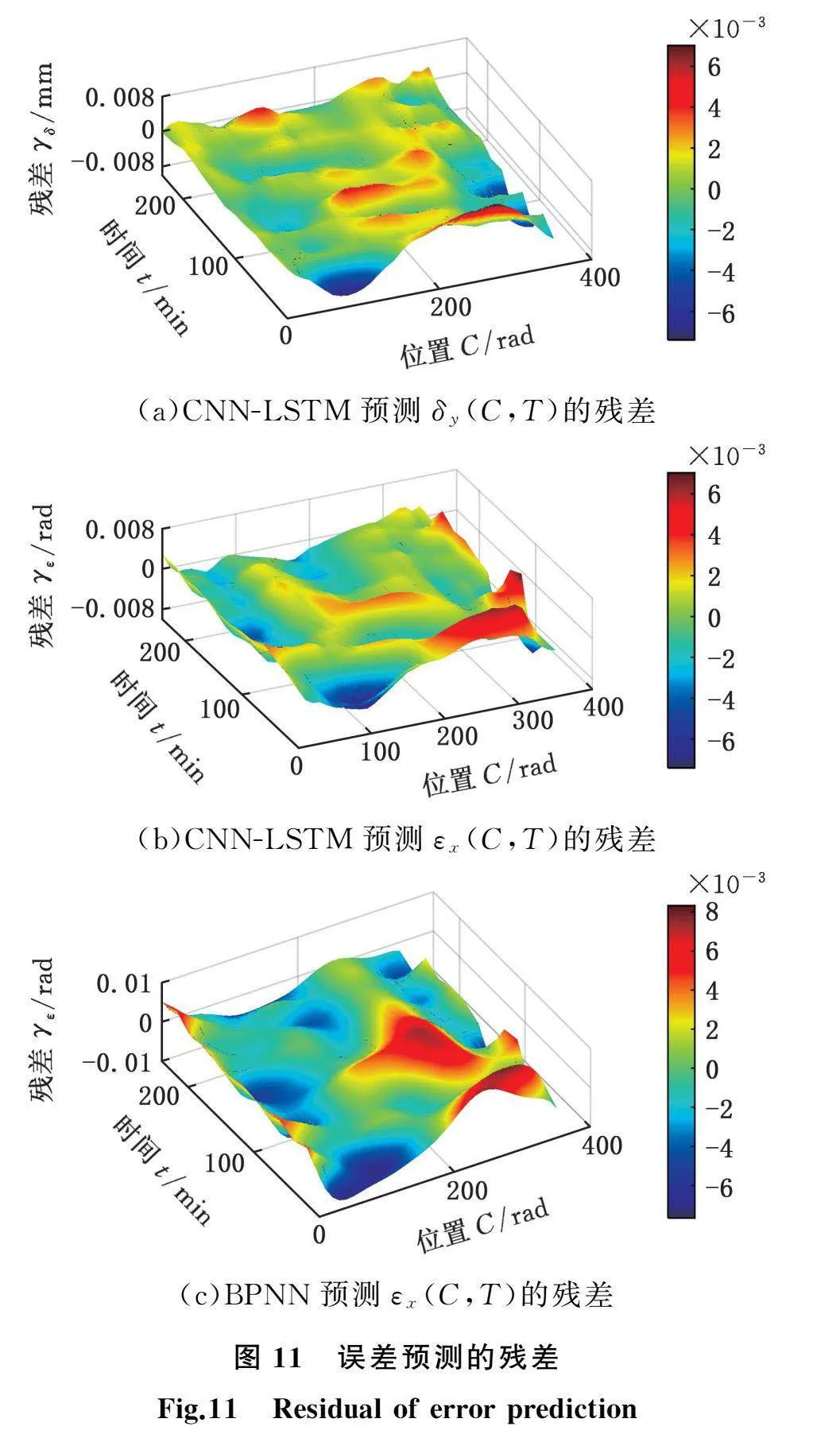
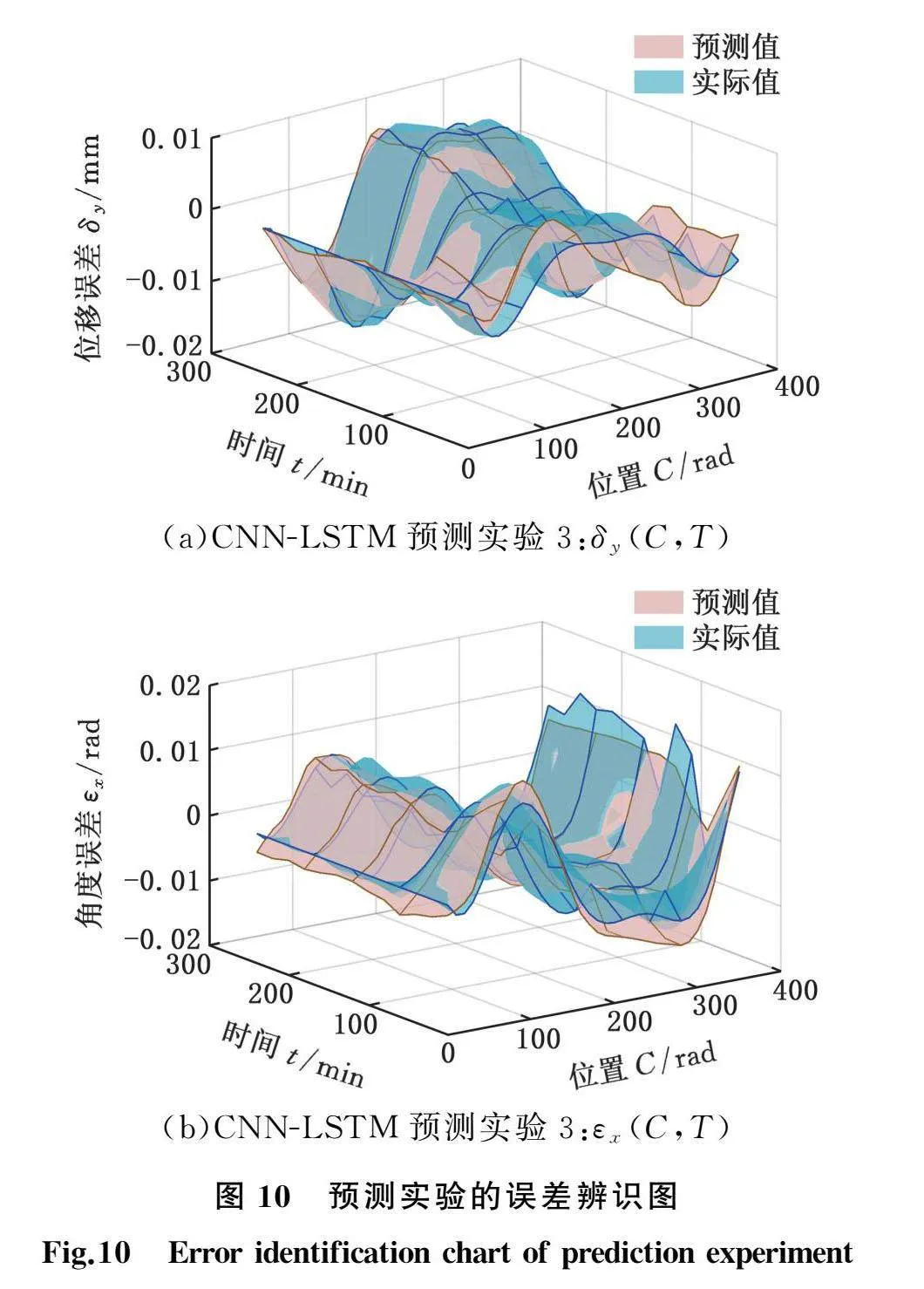
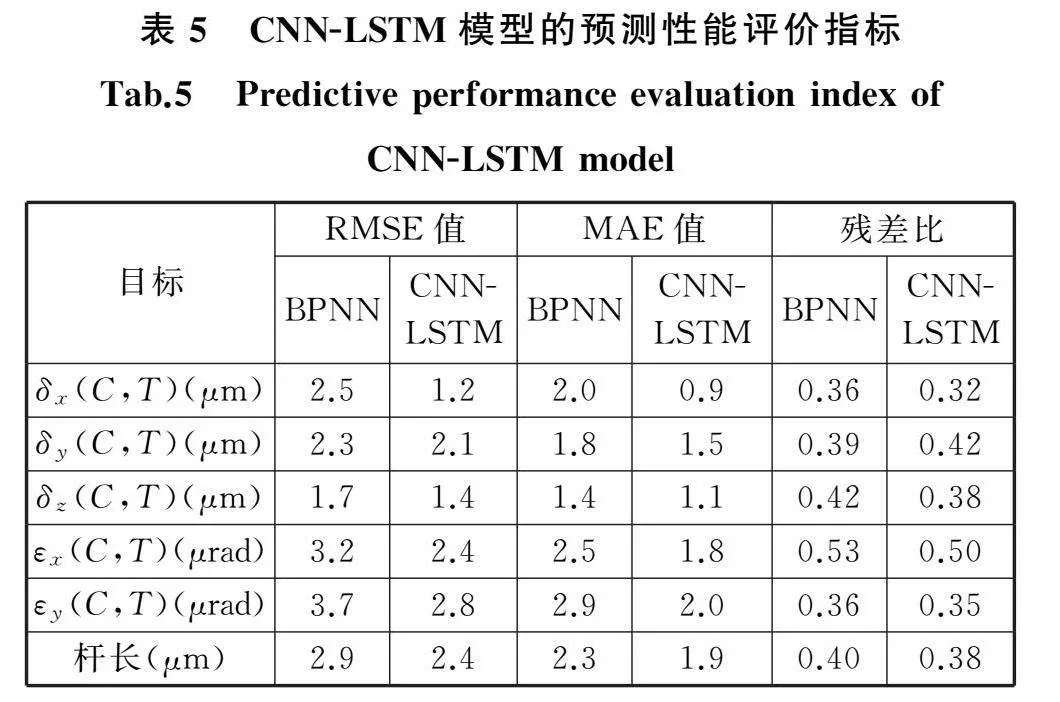
将1、2、4组实验测量的温度、位置和误差数据用于误差建模，将第3组实验的温度和位置数据作为自变量代入模型进行误差预测。通过静/热误差模型进行预测可以得到预测误差，以实验3的δy（C，T）和实验3的εx（C，T）为例绘制位移时间误差变化图（图10）。整体上看，预测值与实际值变化趋势基本吻合。作出残差图（图11），其中，红色部分加深表示残差正向变大，蓝色部分加深表示残差反向变大。误差预测性能指标均方根误差（root mean square error， RMSE）、平均绝对误差（mean absolute error， MAE）和残差比见表5，δy（C，T）最大预测残差值为6.8 μm，而最大误差达17.29 μm，相比之下减幅超过60%，说明能准确地预测出误差。

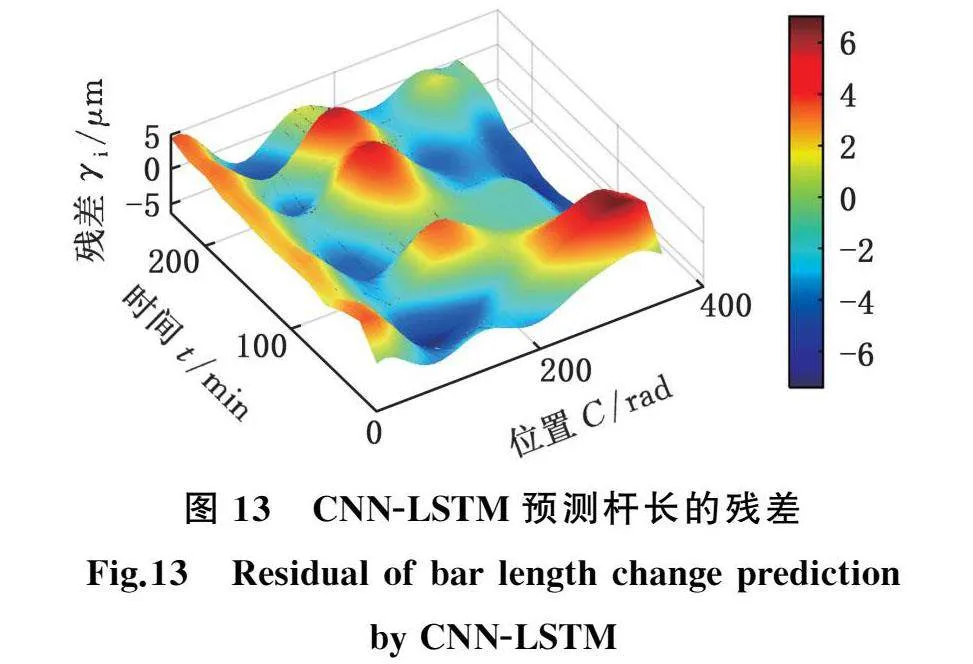
为进一步验证辨识结果的正确性，将预测得到的误差值反算出杆长变化值得到模拟的预测变化杆长。将预测的实验3模式3的杆长变化与实际杆长变化进行对比，绘制杆长变化时间位移变化图（图12），杆长变化的预测性能评价指标见表5，残差图见图13。预测杆长的变化趋势与实际杆长变化趋势基本吻合，而实际杆长的最大偏差已达19.3 μm，预测杆长的最大残差仅7.4 μm，相比之下误差减少61.6%。可以发现预测结果是准确可靠的。

此外，将CNN-LSTM与BPNN神经网络两种模型预测结果进行对比，如表5、图11b、图11c所示，可以发现这两种神经网络的预测结果中残差比相差不大，但是CNN-LSTM预测结果的RMSE值和MAE值要更优于BPNN，说明CNN-LSTM预测结果整体上更加稳定，残差图更加平稳，预测效果更好。

4 结论

（1）本文研究了旋转轴运动特性，构建了基于齐次坐标变化的球杆仪杆长变化模型，将球杆仪

杆长变化映射到旋转轴各项误差，建立了旋转轴多自由度空间误差辨识模型。

（2）提出了静/热误差同步辨识的高效快速测量方法，在满足误差辨识矩阵满秩的前提下，两个中心座一次安装便能完成5种球杆仪测量模式的测量，5种测量模式之间的切换只需要短短几秒，缩短了测量时间，保证了静/热误差测量的可靠性。

（3）建立了CNN-LSTM模型，对静/热误差进行预测，并通过与BPNN模型进行对比，验证了CNN-LSTM模型应用于静/热误差同步建模的优势，实现了对5项静/热位置相关误差及球杆仪杆长的预测，预测杆长最大残差仅7.4 μm，比实际杆长19.3 μm减小60%以上，验证了本文方法的正确性。

本文仅针对旋转轴的5项静/热误差的位置相关误差进行研究，后续可以对静/热误差作用下的旋转轴位置无关几何误差与旋转热定位误差的建模与预测进行研究。

参考文献：

［1］ 吕学祜， 郭前建， 王昊天， 等. 数控机床误差补偿关键技术综述［J］. 航空制造技术， 2022， 65（11）：104-111.

LYU Xuehu， GUO Qianjian， WANG Haotian， et al. Summary of Key Technologies for Error Compensation of CNC Machine Tools［J］. Aeronautical Manufacturing Technology， 2022， 65（11）：104-111.

［2］ LI Yang， YU Maolin， BAI Yinming， et al. A Review of Thermal Error Modeling Methods for Machine Tools［J］. Applied Sciences， 2021， 11（11）：5216.

［3］ 刘阔， 韩伟， 王永青， 等. 数控机床进给轴热误差补偿技术研究综述［J］. 机械工程学报， 2021， 57（3）：156-173.

LIU Kuo， HAN Wei， WANG Yongqing， et al. Review on Thermal Error Compensation for Feed Axes of CNC Machine Tools［J］. Journal of Mechanical Engineering， 2021， 57（3）：156-173.

［4］ DING Shuang， HUANG Xiaodiao， YU Chunjian， et al. Identification of Different Geometric Error Models and Definitions for the Rotary Axis of Five-axis Machine Tools［J］. International Journal of Machine Tools and Manufacture， 2016， 100：1-6.

［5］ British Standards Institution. Test Code for Machine Tools Part 1：Geometric Accuracy of Machines Operating under No-load or Quasi-static Load Conditions：ISO 230-7［S］. Geneva：International Organization for Standardization，2012.

［6］ British Standards Institution. Part 7：Geometric accuracy of axes of rotation：ISO 230-7［S］. Geneva：International Organization for Standardization，2015.

［7］ 项四通， 杜正春， 杨建国. 数控机床几何与热误差测量和建模研究新进展［J］. 机械设计与研究， 2019， 35（6）：52-57.

XIANG Sitong， DU Zhengchun， YANG Jianguo. Recent Advances in Measurement and Modeling of Geometric and Thermal Error of CNC Machine Tools［J］. Machine Design amp; Research， 2019， 35（6）：52-57.

［8］ LI Qingzhao， WANG Wei， ZHANG Jing， et al. All Position-dependent Geometric Error Identification for Rotary Axes of Five-axis Machine Tool Using Double Ball Bar［J］. The International Journal of Advanced Manufacturing Technology， 2020， 110（5）：1351-1366.

［9］ 徐凯， 李国龙， 李喆裕， 等. 基于参数化建模的旋转轴误差快速辨识方法［J］. 仪器仪表学报， 2020， 41（8）：21-29.

XU Kai， LI Guolong， LI Zheyu， et al. Fast Error Identification Method for Rotary Axis Based on Parametric Modeling［J］. Chinese Journal of Scientific Instrument， 2020， 41（8）：21-29.

［10］ ZARGARBASHI S H H， MAYER J R R. Assessment of Machine Tool Trunnion Axis Motion Error， Using Magnetic Double Ball Bar［J］. International Journal of Machine Tools and Manufacture， 2006， 46（14）：1823-1834.

［11］ 梁小冰， 卢耀安， 王成勇. 双转台五轴机床旋转轴位置无关几何误差的辨识［J］. 中国机械工程， 2023， 34（21）：2585-2591.

LIANG Xiaobing， LU Yaoan， WANG Chengyong. Identification of Position-independent Geometric Errors for Rotary Axes of Five-axis Table-tilting Machine Tools［J］. China Mechanical Engineering， 2023， 34（21）：2585-2591.

［12］ FU Guoqiang， FU Jianzhong， XU Yuetong， et al. Accuracy Enhancement of Five-axis Machine Tool Based on Differential Motion Matrix：Geometric Error Modeling， Identification and Compensation［J］. International Journal of Machine Tools and Manufacture， 2015， 89：170-181.

［13］ 郭世杰， 武建新， 乔冠， 等. 数控机床几何误差正弦低次多项式参数化建模与应用研究［J］. 仪器仪表学报， 2020， 41（10）：136-146.

GUO Shijie， WU Jianxin， QIAO Guan， et al. Study on Parametric Modeling and Application of Sinusoidal Low-order Polynomials for Geometric Error of CNC Machine Tool［J］. Chinese Journal of Scientific Instrument， 2020， 41（10）：136-146.

［14］ 李锁， 吴文江， 哈韬， 等. 基于数据驱动的机床热误差补偿技术研究［J］. 小型微型计算机系统， 2019， 40（7）：1569-1572.

LI Suo， WU Wenjiang， HA Tao， et al. Research on Thermal Error Compensation Technology of Machine Tools Based on Data Driving［J］. Journal of Chinese Computer Systems， 2019， 40（7）：1569-1572.

［15］ British Standards Institution. Test Code for Machine Tools—Part 3：Determination of Thermal Effects：ISO 230-3［S］. Geneva：International Organization for Standardization， 2020.

［16］ 魏弦. 数控磨齿机床热误差鲁棒建模技术及补偿研究［D］. 西安：西安理工大学， 2020.

WEI Xian. Study on Robust Modeling and Compensation of Thermal Error for NC Gear Grinding Machine Tool［D］. Xian：Xian University of Technology， 2020.

［17］ 何振亚， 傅建中， 陈子辰. 基于球杆仪检测五轴数控机床主轴的热误差［J］. 光学精密工程， 2015， 23（5）：1401.

HE Zhenya， FU Jianzhong， CHEN Zichen. Thermal Error Measurement of Spindle for 5-axis CNC Machine Tool Based on Ball Bar［J］. Optics and Precision Engineering， 2015， 23（5）：1401.

［18］ WU Chengyang， XIANG Sitong， XIANG Wansheng. Thermal Error Modeling of Rotary Axis Based on Convolutional Neural Network［J］. Journal of Manufacturing Science and Engineering， 2021， 143（5）：051013.

［19］ 徐凯， 李国龙， 李喆裕， 等. 直线轴热定位误差解耦与分步建模研究［J］. 仪器仪表学报， 2022， 43（7）：72-81.

XU Kai， LI Guolong， LI Zheyu， et al. Research on Decoupling and Step-by-step Modelling of Thermal Positioning Error of the Linear Axis［J］. Chinese Journal of Scientific Instrument， 2022， 43（7）：72-81.

［20］ XU Kai， LI Guolong， LI Zheyu， et al. A General Identification Method for Position-dependent Geometric Errors of Rotary Axis with Single-axis Driven［J］. The International Journal of Advanced Manufacturing Technology， 2021， 112（3）：1171-1191.

［21］ LI Bo， TIAN Xitian， ZHANG Min. Thermal Error Modeling of Machine Tool Spindle Based on the Improved Algorithm Optimized BP Neural Network［J］. The International Journal of Advanced Manufacturing Technology， 2019， 105（1）：1497-1505.

［22］ 李彬， 张云， 王立平， 等. 基于遗传算法优化小波神经网络数控机床热误差建模［J］. 机械工程学报， 2019， 55（21）：215-220.

LI Bin， ZHANG Yun， WANG Liping， et al. Modeling for CNC Machine Tool Thermal Error Based on Genetic Algorithm Optimization Wavelet Neural Networks［J］. Journal of Mechanical Engineering， 2019， 55（21）：215-220.

［23］ XIANG Sitong， LU Hongxing， YANG Jianguo. Thermal Error Prediction Method for Spindles in Machine Tools Based on a Hybrid Model［J］. Proceedings of the Institution of Mechanical Engineers， Part B：Journal of Engineering Manufacture， 2015， 229（1）：130-140.

［24］ 王培桐， 范晋伟， 任行飞， 等. 基于热传导和卷积神经网络的磨床主轴热误差预测［J］. 光学精密工程， 2023， 31（1）：129-140.

WANG Peitong， FAN Jinwei， REN Xingfei， et al. Thermal Error Prediction for Grinding Machine Spindle Based on Heat Conduction and Convolutional Neural Network［J］. Optics and Precision Engineering， 2023， 31（1）：129-140.

［25］ HOCHREITER S， SCHMIDHUBER J. Long Short-term Memory［J］. Neural Computation， 1997， 9（8）：1735-1780.

［26］ LIU Jialan， MA Chi， GUI Hongquan， et al. Thermally-induced Error Compensation of Spindle System Based on Long Short Term Memory Neural Networks［J］. Applied Soft Computing， 2021， 102：107094.

［27］ GUO Jiahao， XIONG Qingyu， CHEN Jing， et al. Study of Static Thermal Deformation Modeling Based on a Hybrid CNN-LSTM Model with Spatiotemporal Correlation［J］. The International Journal of Advanced Manufacturing Technology， 2022， 119（3）：2601-2613.

（编辑 陈 勇）