基于自适应闭环反馈的高空车臂架避障控制研究

摘要：针对改进梯度投影法在混合式高空作业车应用中出现的速度、轨迹不连续以及避障过程中末端速度突变等问题，提出了一种基于自适应闭环反馈的高空车臂架避障控制算法。对改进梯度投影法进行优化，实现了存在伸缩臂的高空车臂架与末端的速度、轨迹连续的运动控制。采用伪距离描述臂架与障碍物的接近程度，对传统避障速度算法进行优化，并提出一种自适应闭环反馈方法，将反馈权重与伪距离相关联，使反馈权重自适应变化。所提算法在保证末端轨迹精度的同时大大改善了臂架关节在避障过程中的速度突变。仿真及半物理实验结果表明，相较于传统方法，所提方法速度变幅大大减小且轨迹更加平滑，实现了多障碍物避障与同一障碍物多次避障。

关键词：伪距离；避障；冗余臂架；梯度投影法；高空作业车；闭环反馈

中图分类号：TH6

DOI：10.3969/j.issn.1004132X.2024.08.018

开放科学（资源服务）标识码（OSID）：

Research on Obstacle Avoidance Control of Booms of Aerial Work Platforms

Based on Adaptive Closed-loop Feedback

HUANG Yi HU Ming TANG Qiying GUO Jinmeng ZHANG Jinlai REN Guangan

College of Automotive and Mechanical Engineering，Changsha University of Science and

Technology，Changsha，410114

Abstract： In order to solve the problems of discontinuity of velocity and trajectory in the applications of the improved gradient projection method in hybrid aerial work platforms and the problems of abrupt change in velocity of ends during obstacle avoidance， an obstacle avoidance motion control algorithm was proposed based on adaptive closed-loop feedback. The improved gradient projection method was optimized to realize the continuous motion control of the speed and trajectory of the booms and the ends of aerial work platforms with telescopic arms. The pseudo distance was used to describe the proximity between the boom and the obstacle， and the traditional obstacle avoidance speed algorithm was optimized. An adaptive closed-loop feedback method was proposed， which correlated the feedback weight with the pseudo-distance， and made the feedback weight change adaptively. The algorithm guaranteed the precision of the end trajectory， and greatly improved the sudden changes in the boom joint velocity in the course of obstacle avoidance. Simulation and semi-physical experimental results verify that the speed amplitude of the proposed method is greatly reduced and the trajectory is smoother than that of the traditional method， and multi-obstacle avoidance and multiple obstacle avoidance may be realized.

Key words： pseudo-distance； obstacle avoidance； redundant boom； gradient projection method； aerial work platform； closed loop feedback

0 引言

自动化施工是高空作业车的重要技术发展方向，高空作业车的自动化作业中最重要的两个环节是末端避障以及臂架控制。末端避障中碰撞检测方法是不可缺少的一环，而碰撞检测并不受限于使用对象，故对高空作业车同样可以参考机器人所使用的碰撞检测方法。目前国内外对碰撞检测的方法有欧氏距离、C空间方法、伪距离等［1-3］。KHAN等［4］采用GJK（Gilbert-Johnson-Keerthi）算法，该算法直接以机器人与障碍物之间的距离作为碰撞指标，意味着该算法适用于任意形状的机械手以及障碍物，但无疑会增加计算量。PARK等［5］以人工势场法作为碰撞指标，该方法适用性广，但具有搜索量大、容易产生局部最小值以及奇异点等缺点。XU等［6］为使机器人与障碍物之间的距离描述更加简单，将机器人和障碍物分别抽象为临界点集，通过一般的K类函数以不等式约束的形式建立避障策略。JU等［7］根据机械臂几何构型提出了一种基于三角碰撞平面的可预测避障模型。MU等［8］考虑到最小欧氏距离精度高、效率低以及伪距离精度低效率高的特点，采用最小欧氏距离结合伪距离的方法来实现避障的碰撞检测。张建华等［9］采用二分试探的碰撞位置检测算法，但需要进行多次迭代计算，这样必然导致计算量增大。

高空作业车根据结构特点大致可以分为直臂式、折臂式、垂直升降式和混合式［10］。在臂架控制方面，针对不同结构特点的高空作业车，往往需要采取不同的控制方法。滕儒民等［11］提出了一种基于启发式路径搜索的避障路径规划方法，他们将高空作业车的臂架作为冗余自由度的机械臂并对机械臂进行分析，建立运动学模型后在MATLAB中验证了启发式A*算法的可行性，为大型高空作业车的轨迹规划提供了有效的运动控制方案，但该方法仅研究末端路径轨迹且未考虑关节规划。王硕等［12］给出了一种直臂式高空作业车的作业平台轨迹跟踪控制方法，针对所研究的高空作业车建立了基于机械臂油压系统的控制模型并设计了PID控制器，实现了作业平台的轨迹跟踪控制，以及高空作业车末端直线运动及刷墙运动，该方法控制简单，但难以实现复杂运动且未考虑避障要求。混合式高空作业车的臂架结构不同于一般形式的高空作业车，它可视为具有冗余自由度的机械臂，故对于混合式高空车可以参考冗余机械臂的控制方法：梯度投影法、增广雅可比方法、加权最小范数法以及基于以上方法的各种衍生方法等［13-15］。KORKMAZ等［16］提出一种针对欠驱动水下航行器机械手系统的逆运动学控制方法，通过仿真证明了该控制方法在参数不确定并存在干扰因素的情况下依旧有效。PENG等［17］提出一种适用于分段连杆索驱动超冗余机器人的轨迹跟踪控制方法，以主动索张力和末端执行器位姿为优化指标，采用动态前馈控制和PD控制相结合的方法构建了轨迹跟踪框架，通过联合仿真系统验证了所提方法的有效性。MARCOS等［18］通过结合闭环伪逆方法与多目标遗传算法实现了关节位置的控制，并进行仿真研究，实现了对冗余度机械手的轨迹控制优化。WAN等［19］受到经典加权最小范数（weighted least-norm， WLN）和流行的梯度投影法（gradient projection method， GPM）优点的启发，提出了一种求解冗余机械手多性能指标的逆运动学（inverse kinematics， IK）问题的加权梯度投影法，通过仿真和实验与传统的WLN和GPM方法的结果进行比较，验证了所提方法的有效性，但该方法存在关节速度变化快的问题。ZHANG等［20］为了满足空间在轨服务的安全要求，提出了一种基于改进粒子群算法的避障轨迹规划方法，但该方法仅简单地考虑了关节规划，未考虑速度层面的约束。XIE等［21］提出了一种基于快速探索随机树算法和正反向运动学算法的避障与路径规划算法，以较低的计算成本为多关节机械臂找到无碰撞的可行路径，但该方法仅规划末端避障路径，未考虑速度的连续性。LI等［22］针对超冗余度机械臂的避障路径规划和离散轨迹跟踪问题，提出了一种集成优化方法，该综合优化方法能够快速搜索出合适的轨迹，指导机械手在实现避障和满足关节约束的同时获得目标。LIU等［23］针对冗余度机械臂运动过程中的碰撞问题，提出了一种基于多目标优化的末端执行器轨迹规划方法，该方法在完成避障的同时使得关节轨迹光滑且能量消耗低。上述研究存在着仅研究末端路径轨迹而未考虑关节规划与速度的连续，各种研究目标的关节多由旋转关节组成，少有存在移动关节的研究对象，对于高空车臂架控制的自动化控制方式简单且效果欠佳，难以实现复杂运动等问题。

本文基于改进梯度投影法以及传统速度避障法，提出一种适用于混合式高空作业车的基于自适应闭环反馈的避障控制算法。通过基于加权最小范数解的二次臂架运动分配方法，实现对存在移动关节的高空车臂架与末端的速度、轨迹连续的运动控制。采用伪距离来评估臂架与障碍物的接近程度，并对传统避障速度方法进行改进。在闭环反馈方面，提出一种自适应闭环反馈方法，在避障后保证末端能够回到运行轨迹的同时速度不会发生突变。以15 m混合式高空作业车为研究对象，开展了高空车臂架避障运动控制的仿真与半物理实验研究，验证该算法在高空车臂架避障过程中的可行性及平稳性。

1 高空车臂架运动学分析

1.1 臂架正运动学

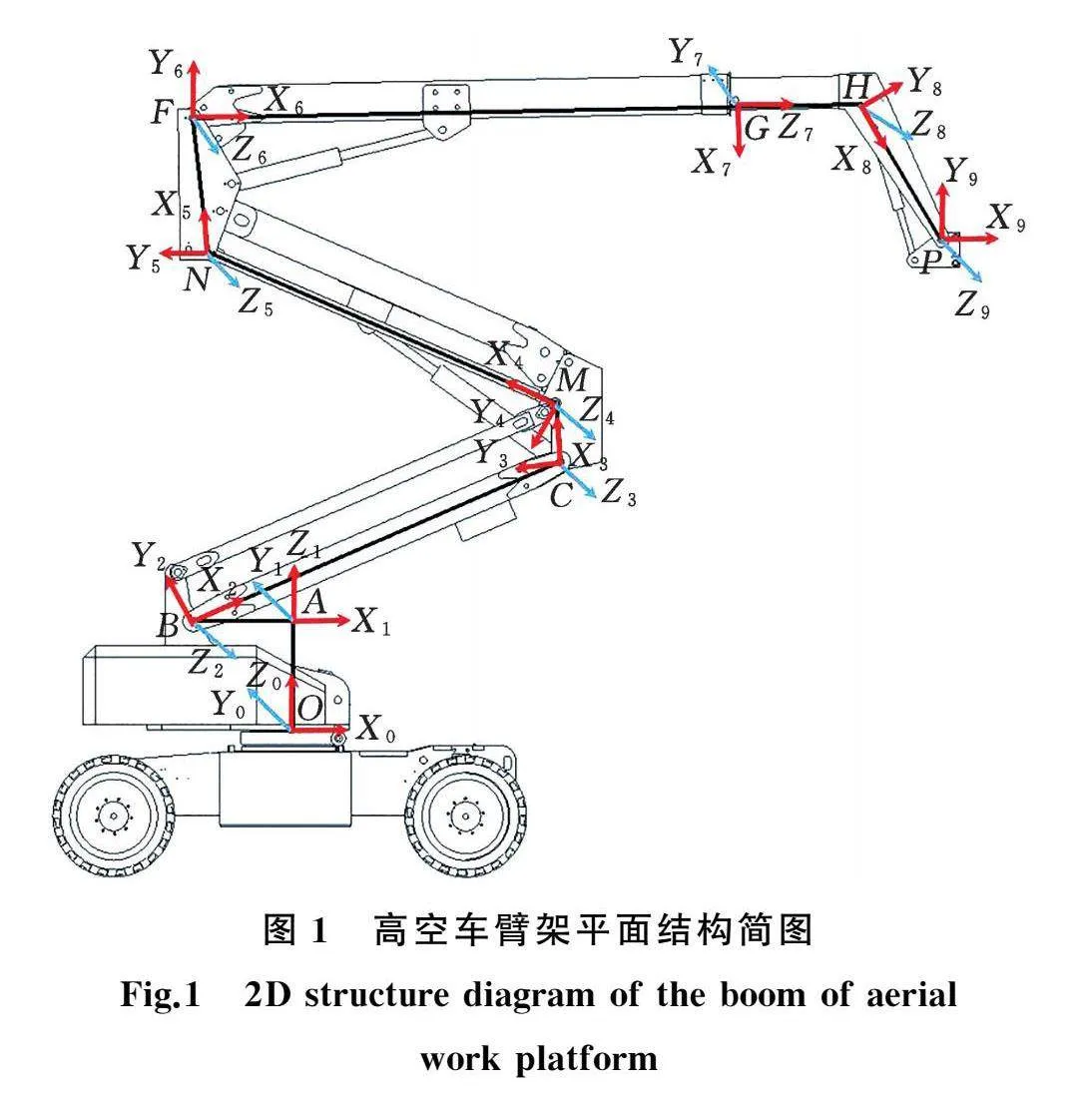
混合式高空作业车臂架可以看作冗余机械臂，由于研究对象高空作业车臂架系统结构复杂，故建模时将其看作九自由度冗余机械臂，将高空车臂架看作刚性结构，便可进行运动学分析。由于混合式高空作业车的结构特点，各关节之间存在一定几何关系，在实际驱动时只需要对回转、塔臂、主臂、伸缩臂四个臂架进行驱动，采用改进D-H法对混合式高空作业车臂架系统进行正运动学分析，其平面结构简图见图1（图1中，蓝色箭头为垂直纸面方向，关节1和7均为垂直纸面向内其余均向外，关节7与8为重叠关节，为方便理解，将两关节分开绘制）。

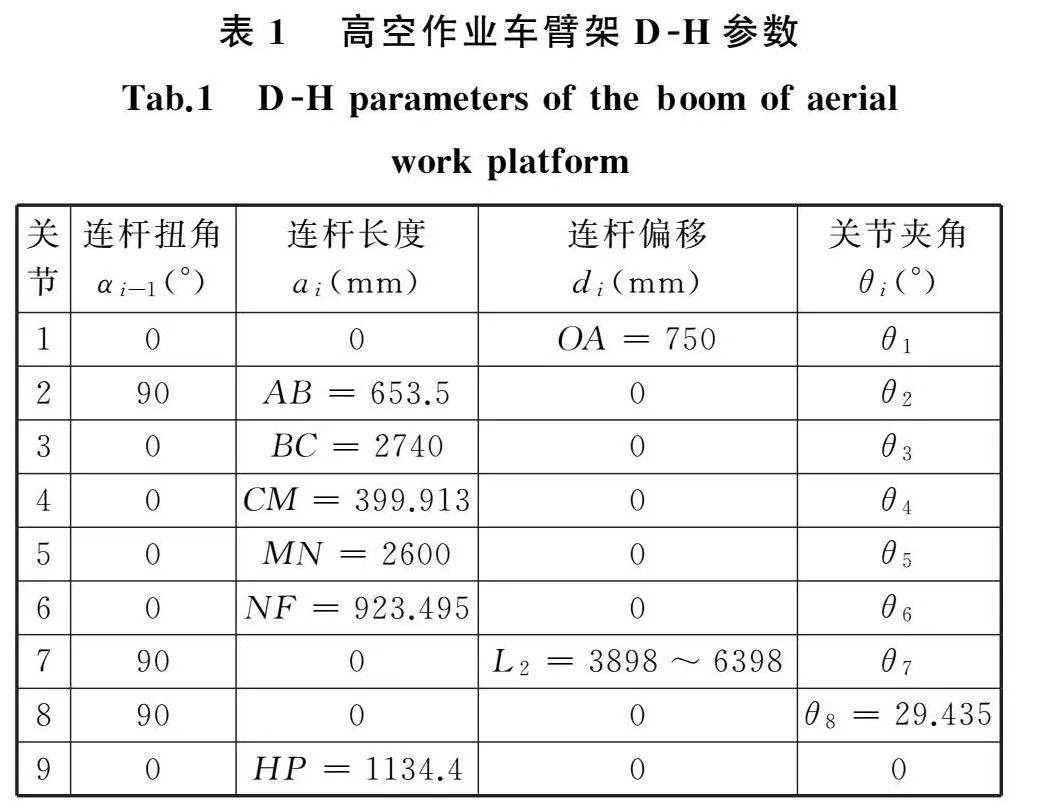
图1中，关节1为回转关节，关节2、3、4、5组成塔臂部分，关节6为主臂，关节7为伸缩臂，并令FH长度为L2，建模后通过结构公式可对末端坐标公式进行简化，只需通过四个关节参数即可计算出末端坐标，D-H参数见表1。

由于高空车末端一般配有载物平台且平台通过液压自动调平，故假设末端存在连杆JP且恒保持水平状态，考虑到伸缩臂的关节的存在，令θ7=-180°，连杆JP长度LJP=1800 mm，故根据D-H法可求得末端坐标P：

x=c1（LJP-LAO+LBCc2+LCMc23+LMNc234+

LNFc2345+L2s23456-LHPc234568）

y=s1（LJP-LAO+LBCc2+LCMc23+LMNc234+

LNFc2345+L2s23456-LHPc234568）

z=LAB+LBCs2+LCMs23+LMNs234+LNFs2345-

L2c23456-LHPs234568（1）

式中，LJP为JP长度，其余类推；ci=cos θi；si=sin θi；cij=cos（θi+θj）；sij=sin（θi+θj）。

根据高空作业车臂架结构，有θ2=f1（θ4）， θ3=f2（θ4），θ5=f3（θ4），θ8=29.4346°，则式（1）变形为仅与θ1、θ4、θ6、L2相关的公式P（θ1，θ4，θ6，L2），求得臂架雅可比矩阵：

J（θ）=xθ1xθ4xθ6xL2

yθ1yθ4yθ6yL2

zθ1zθ4zθ6zL2（2）

1.2 臂架逆运动学

考虑混合式高空作业车结构特点，采用改进梯度投影法对其进行逆运动学求解，以实现对末端的控制。

设混合式高空作业车臂架末端速度x·=［x·1 x·2 … x·m］T，而各关节角速度或位移速度θ·=［θ·1 θ·2 … θ·n］T，根据逆运动学，有

x·=J（θ）θ·（3）

式中，J（θ）为上文提到的雅可比矩阵，J（θ）∈Rm×n。

mlt;n时，得到上式的加权最小范数解：

θ·=W-1JT（JW-1JT）-1=J+Wx·（4）

式中，J+W为J（θ）的加权广义逆矩阵；W为加权对称正定对角矩阵。

W∈Rm×n，其对角元素为

Wi，j=1+|H（θi）|（5）

H（θi）=（θiM-θim）2（2θi-θiM-θiM）4（θi-θiM）2（θi-θim）2（6）

式中，θi为第i个关节转角或位移量；θiM为关节转角或位移量最大值；θim为关节转角或位移量最小值。

通过最大最小值的约束可以将各关节限制在合适的范围内，由以上公式可知，当θi→θiM或θi→θim时，H（θi）→∞， W-1ij→0，此时关节i停止运动；当θi→（θiM+θim）/2时，H（θi）→0，W-1ij→1，此时关节运动不再受限。为辨别关节是在远离还是趋近最值，同时考虑到计算时由于精度不足可能导致θi超过最值，而此时H（θi）不为0会导致关节继续运动，故当关节量超出最值时需使Wi，j=∞，使关节停止，但如果关节速度为远离极限值方向，则无需变化，故将加权因子及H（θi）重新定义为

H（θi）=∞""" θigt;θiM，θilt;θim

H0（θi）θim≤θi≤θiM（7）

H0（θi）=（θiM-θim）2（2θi-θiM-θiM）4（θi-θiM）2（θi-θim）2

而

Wi，j=1+|H（θi）|" Δ|H（θi）|≥0

1Δ|H（θi）|lt;0（8）

其中，Δ|H（θi）|为|H（θi）|的变化率。以上公式说明，当关节量θi处于最值附近且关节速度为远离极限值方向时，运动状态会发生改变，故可以保持运动。但当关节量超过最值且Δ|H（θi）|≥0时，关节保持静止。当Δ|H（θi）|lt;0时，关节可以运动。

在此基础上加入末端位置闭环反馈，得到加入末端位置反馈的加权闭环逆运动学算法公式：

θ·=J+W（x·+K（pd-pe））（9）

式中，K为单位正定矩阵；pd为臂架末端预期坐标；pe为臂架末端实际坐标。

1.3 二次臂架运动分配

混合式高空作业车通过协调回转、塔臂、主臂及伸缩臂进行臂架运动控制。其中，伸缩臂为移动关节，回转、塔臂与主臂关节均为转动关节，分别对应位移变量和转角变量。采用式（9）计算加权对称正定对角矩阵Wi，j时会优先驱动塔臂及主臂协调运动，而伸缩臂被“视为”固定长度的连杆。末端垂直运动时，末端达到一定位置（例如主臂水平）时，采用该公式会优先通过塔臂、主臂实现末端垂直运动，此时就会出现速度、轨迹突变现象。

本文提出了一种基于加权最小范数解的二次臂架运动分配方法。考虑到塔臂在高空车臂架作业特点以及在运行过程中仅影响末端点Z轴坐标，将末端速度拆解为两部分，各部分所占权重与塔臂角度θ4相关，将式（9）改写为

θ·=J+W1（x·+K（pd-pe））（1-θ4M-θ4θ4M-θ4m）+

J+W2（x·+K（pd-pe））θ4M-θ4θ4M-θ4m（10）

J+W1=W-11JT（JW-11JT）-1

J+W2=W-12JT（JW-12JT）-1

W1=W11

∞

W33

W44

W2=W′11

W′22

∞

W′44

式中，J+W1、J+W2分别为令θ·4、θ·6为0的加权广义逆矩阵。

式（10）表明，将末端位移的实现分解为两部分，分别通过θ1、θ4、L2与θ1、θ6、L2实现末端运动即第一次臂架运动分配。而两者实现末端运动的占比与塔臂角度θ4相关，当θ4越接近θ4M，式（10）中等号右边前一项占比越小，后一项占比越大，即θ4越接近θ4M，θ1、θ4、L2实现更少的末端速度，θ1、θ6、L2实现更多的末端速度，即第二次臂架运动分配。通过此方法保持总体末端速度不变。此方法在合理分配各关节的同时保证末端运动、各关节速度变化连续平滑，能实现混合式高空作业车臂架逆运动学控制。

2 碰撞检测与避障控制

2.1 碰撞检测

实现避障最主要是判断臂架与障碍物是否产生碰撞，现有判断方法有很多种并且可以互相结合，考虑到高空作业车体积大且精度要求比小型机械低，故以效率较高的伪距离作为臂架与障碍物之间的碰撞检测指标。

对于障碍物的建模，通常用一个或多个规则空间包络来进行拟合，采用超二次曲面描述三维空间中的物体，统一的超二次曲面解析式如下：

（x-x0h1）2m+（y-y0h2）2n+（z-z0h3）2p=1（11）

式中，（x0，y0，z0）为超二次曲面中心点坐标；（x，y，z）为拟合障碍物形状的超二次曲面上任意一点坐标；m、n、p和h1、h2、h3分别为描述超二次曲面形状的形状参数与体积参数。

则根据上式可以定义空间任意一点到超二次曲面的伪距离表达式：

dp（x，y，z）=（x-x0h1）2m+（y-y0h2）2n+

（z-z0h3）2p-1（12）

本文研究的混合式高空作业车通常用于喷涂作业、玻璃安装等，工作中遇到的障碍物多为墙体结构的突出部分或电线，且考虑到避障轨迹的顺滑及计算效率，本文障碍物以三维空间圆柱体为例，其伪距离表达式为

dp（x，y，z）=（x-x0R）2+（y-y0R）2+（z-z0H）8-1（13）

式中，R为圆柱体拟合半径；H为圆柱体拟合高度。

三维空间任一点与拟合的超二次圆柱体曲面存在三种位置关系：伪距离dp（x，y，z）lt;0时，表示空间点（x，y，z）位于圆柱体内部，此时高空作业车臂架已和障碍物发生碰撞；dp（x，y，z）=0时，表示空间点（x，y，z）位于圆柱体曲面上，此时高空作业车臂架刚与障碍物发生碰撞；dp（x，y，z）gt;0时，表示空间点（x，y，z）位于圆柱体外部，此时臂架与障碍物未产生碰撞，如图2所示。同时，伪距离越大，空间点离障碍物越远，故可以用伪距离来进行碰撞检测与避障。

根据式（13）定义某一臂架i到障碍物的伪距离为臂架任一点到障碍物表面伪距离的最小值，即

dp，i=min（dp（P0，i），…，dp（Pj，i），…，dp（Pn，i））

式中，P0，i、Pn，i分别为臂架i的首末端点；Pj，i为臂架i的中间任一点，点的数量越多，精度越高但计算量越大。

对于高空作业车臂架系统，整个高空作业车臂架到障碍物的伪距离定义为

dp=min（dp，1，…，dp，i，…，dp，8）

式中，dp，1、dp，8分别为臂架1和8的伪距离；dp，i为臂架i的伪距离。

考虑到高空作业车工作中多面向墙体，且末端常搭载机械手配合工作，一般情况下其他臂架均无需避障，所以取最后一节臂与障碍物的伪距离作为碰撞检测指标不仅满足避障需求，还能提高计算效率。当环境中存在N个障碍物时，同样取最后一节臂架与N个障碍物之间的最小伪距离值即可，即

De=min（dp1，…，dpi，…，dpN）（14）

2.2 基于伪距离的避障算法及优化

为实现避障与控制避障距离，通常会设定一个阈值dm，随后根据式（14）计算得到伪距离De，当Delt;dm时赋予臂架末端避障速度vp，方向沿障碍物超二次曲面中心指向臂架上最小伪距离值对应点，传统避障速度计算公式如下：

vp=0" Degt;dm

vDe≤dm（15）

v=vm2（cos（πDedm）+1）np‖np‖（16）

式中，vm为最大避障速度；np为由障碍物拟合超二次曲面中心指向臂架末端点的矢量。

此时式（10）改写为

θ·=J+W1（x·+vp+K（pd-pe））（1-θ4M-θ4θ4M-θ4m）+

J+W2（x·+vp+K（pd-pe））θ4M-θ4θ4M-θ4m（17）

以上方法虽能够实现避障但存在一定问题，传统的伪距离避障方法中，np为障碍物拟合超二次曲面中心指向臂架标志点的矢量，当障碍物中心不在末端运行轨迹上时，该计算方法得到的np会指向非理想方向，对于高空作业车必然导致避障轨迹不合理甚至避障失败。同时，该方法用于作为工程机械的高空作业车，在避障以及回到预期点时会产生较大的末端速度且速度变化快，即使能够实现也会给各关节带来巨大的冲击。导致这一现象有两个原因，首先为实现避障与闭环反馈相平衡，需要通过不断试错来选择合适的避障速度，为与闭环反馈平衡，往往合适的避障速度都会较大。其次在避障时臂架末端实际点相较于预期点会产生偏移，随着末端实际点离预期点越远，闭环反馈作用越大，为使末端实际点回到预期点，必然会产生较大的速度。但如果将避障速度减小将导致避障失败，若将闭环反馈参数K减小则会导致末端无法回到轨迹。

由式（15）、式（16）发现，避障速度在伪距离由阈值dm减小到0的过程中不断增大，在末端刚进入避障区域时被赋予的避障速度较小，臂架末端仍沿原轨迹运行且继续向障碍物靠近，所以用式（15）、式（16）计算避障速度时有可能出现臂架离障碍物过近的现象，部分情况下还会导致避障失败，通过调整阈值dm也难以实现最小伪距离的控制，故为方便控制最小伪距离，提出绝对阈值与设定阈值，将式（15）、式（16）改写为

vp=0""""" Degt;dm

vdm≥Degt;dc

vmnp‖np‖De≤dc（18）

v=vm2（cos（πDe-dcdm-dc）+1）np‖np‖（19）

其中，dc为绝对阈值，原公式伪距离达到0时避障速度才达到最大，改写后伪距离达到绝对阈值时即可达到避障速度最大值。

2.3 避障方向矢量计算以及标志点的选取

由于np定义为由障碍物拟合超二次曲面中心指向臂架末端点的矢量，当障碍物中心不在末端运行轨迹上时，np会指向非理想方向，可能导致避障轨迹不合理，一些工况下更意味着避障失败。为解决这一问题，将np重新定义如下：

np=pei-po

式中，pei为末端标志点坐标；po为障碍物标志点坐标。

对于圆柱体障碍物，障碍物标志点为末端点到障碍物拟合超二次曲面的中心轴线的垂点。综合考虑高空作业车结构特征以及高空作业车多面向墙体作业等因素，末端通常应向臂架所在侧避障。同时为使避障轨迹平滑，制定末端标志点选择策略如下：首先将末端臂架分为N份，此时末端臂架存在N+1个待选择点，随后从末端点开始，计算障碍物标志点到待选择点的矢量与末端臂架的角度，选择第一个使该角度为钝角或更大角度的待选择点为末端标志点，此时即便障碍物中心相对于运行轨迹存在偏移，仍能成功实现避障并且速度变化更加平滑，但存在速度较大的问题。考虑到末端臂架各点速度方向平行以及末端速度的稳定，避障速度仍然赋予末端点而非末端标志点。

以将末端杆分为5份为例，示意图见图3。图3中，O为障碍物标志点，末端杆件存在5个待选择点，其中障碍物标志点到点1、2、3的矢量与末端臂架之间的角度均为钝角，但障碍物标志点O到点3的矢量为从末端点5开始计算的第一个与末端臂架为钝角的矢量，故选择点3作为末端标志点。

2.4 设计自适应闭环反馈

传统闭环反馈方法是利用末端预期点与末端实际点的位置差进行闭环反馈，即赋予末端由末端实际位置指向末端预期位置的速度。避障时实际点必然会与预期点产生位置差，由式（9）可知K不变的情况下，位置差越大，闭环反馈产生的速度越快，当避障结束时避障速度骤降加上实际点与预期点位移差大，导致末端速度突变。闭环反馈产生的速度可分解为平行于运行轨迹的速度以及垂直于运行轨迹的速度，平行于运行轨迹的速度对末端回到运行轨迹并无帮助，故舍弃该速度，将闭环反馈方向由原来的实际点到预期点改为实际点到运行轨迹。该方法保证末端回到运行轨迹的同时，减小由闭环反馈引起的速度过快与突变，从而改写式（17）如下：

θ·=J+W1（x·+vp+K（pn-pe））（1-θ4M-θ4θ4M-θ4m）+

J+W2（x·+vp+K（pn-pe））θ4M-θ4θ4M-θ4m（20）

其中，pn为末端实际点到运行轨迹的垂足坐标，以末端运行到O点为例，示意图见图4，图中O为末端实际点，v为运行速度单位向量，N为末端实际点到运行轨迹的垂足点，B为预期点，黑色实线为避障轨迹，虚线为运行轨迹，蓝色箭头ON为末端实际点指向运行轨迹方向的向量即自适应闭环反馈方向，橙色箭头OB为末端实际点指向末端预期点的向量即传统闭环反馈方向。

图4中，N点坐标为pn=（xn，yn，zn）。闭环反馈幅值方面，传统方法中K是不变的，若K设定过大，会导致无法避障，设定过小会导致末端回到运行轨迹速度较慢，即使K取得合适的值，当避障实际点与预期点之间存在较大位置差时，仍会导致速度过快。针对此问题，提出一种根据伪距离自动调节的自适应闭环反馈Ke值，首先设定最大Kem值，在未避障时Ke≡Kem，一旦进入阈值范围，标志点到障碍物的伪距离越来越小，Ke值也相应减小，即末端离障碍物越近，闭环反馈对末端运动的影响越小，使得末端成功避开障碍物。当末端远离障碍物，伪距离逐渐变大，使得Ke值逐渐变大，此时闭环反馈的影响加大，让末端能够从避障轨迹回到运行轨迹，这样既能保证末端的避障轨迹，又能保证末端回到运行轨迹。Ke值计算公式如下：

Ke=Kem" Degt;dm

Keidm≥Degt;dc

0De≤dc（21）

Kei=Kem（1-cos（πDedm））

式中，Kem为最大闭环反馈值。

从而式（20）改写为

θ·=J+W1（x·+vp+Ke（pn-pe））（1-θ4M-θ4θ4M-θ4m）+

J+W2（x·+vp+Ke（pn-pe））θ4M-θ4θ4M-θ4m（22）

由式（21）可以看出，Ke可以根据当前伪距离自动调整大小，故无需再设置较大的避障速度vm与之“对抗”，且自适应闭环反馈能够在避障结束末端开始远离障碍物时使末端准确回到运行轨迹，从而消除末端误差。

2.5 速度整合

由式（22）可以看出臂架末端的实际移动速度由运行速度x·、避障速度vp、闭环反馈Ke（pn-pe）三个部分组成。其中，vp、Ke（pn-pe）会根据末端与障碍物的伪距离变化，导致末端实际移动速度的变化，并且避障速度方向与运行速度方向往往呈反向，使得避障前期的末端实际移动速度较慢，避障后速度较快，故采用速度整合方法。通过将三部分的速度合成，使得避障速度与闭环反馈不影响末端速度大小，仅改变速度方向，保证末端速度恒定的同时实现避障，具体公式如下：

ve=vv（vp+x·）‖vp+x·‖+Ke（pn-pe）‖v（vp+x·）‖vp+x·‖+Ke（pn-pe）‖（23）

式中，v为设定速度。

将式（22）改写后，得到最终的逆运动学算法公式：

θ·=J+W1（ve）（1-θ4M-θ4θ4M-θ4m）+J+W2（ve）θ4M-θ4θ4M-θ4m（24）

3 仿真与实验分析

3.1 仿真分析

为验证本文算法的有效性和优越性，以15 m混合式高空作业车为研究对象，分别采用传统伪距离避障方法和本文避障方法，在同等初始条件下进行仿真对比。其中，初始关节量θ1、θ4、θ6、L2分别为-25°、65.1287°、12.5878°、6387 mm，末端速度方向均为沿y轴正方向。为加快仿真进度，运行速度与设定速度均为100 mm/s，避障速度幅值分别为7500 mm/s与100 mm/s，两种方法的闭环反馈参数均为3，传统避障方法的伪距离阈值为5，本文采用的避障方法设定阈值为10、绝对阈值为5，拟合后障碍物中心点的坐标为（7338.8 mm，0 mm，3329.42 mm）。仿真结果见图5。图5a、图5d从轴测图与俯视图两个角度展示轨迹姿态变化。

对比图5a、5d可以发现本文末端轨迹更加平滑，对比图5b、图5e及图5i、图5l可以发现本文方法中各关节速度变化更加平稳、速度更小且在避障以及末端回到轨迹时末端速度依旧保持不变。传统伪距离避障方法中伸缩臂及回转最大速度分别达到1538 mm/s与24.5°/s，而本文方法中这两个关节最大速度仅为99 mm/s与0.94°/s，在同样的运行速度下本文方法的最大速度平均减小约94.83%，证明本文方法更适合工程机械。图5g、图5j中红色虚线分别对应传统伪距离避障算法中的阈值与本文避障算法的绝对阈值，通过对比可以发现本文方法对最小伪距离的控制更加明显，能够通过绝对阈值来直接控制最小伪距离从而实现控制末端到障碍物的距离。对比图5h与图5k发现末端同样具有回到运行轨迹的能力。综上所述，本文方法在成功避障的基础上，较好解决了各关节速度变化快、速度大以及障碍物中心相较于运行轨迹产生偏移时避障轨迹错误等问题，并且相较于传统的伪距离避障方法，本文方法能够更方便地控制最小伪距离值。

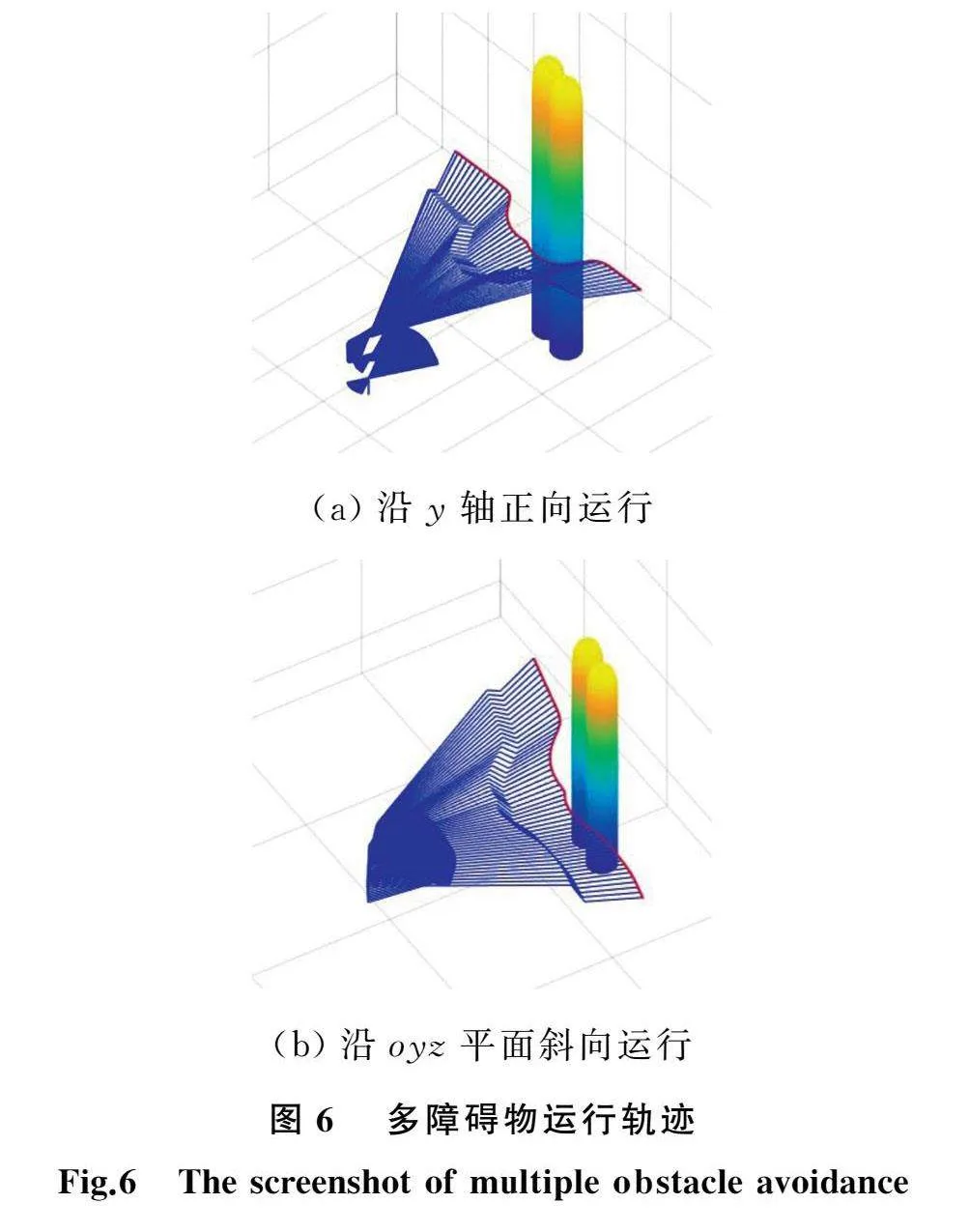
同时，本文避障算法可以实现横向运行以及斜向运行时的多障碍物避障。以空间同时存在两障碍物为例进行仿真，障碍物中心坐标分别为（7012.65，0，3329.42）mm和（6812.65，－1000，3329.42）mm。图6a中运行速度为100 mm/s、方向为沿y轴正方向，图6b中运行速度为100 mm/s、方向为yoz平面内与y轴正方向呈45°斜向运行，由图6可以看出两种情况下均实现了避障，证明本文方法在多障碍物情况下同样能够实现避障。

3.2 半物理实验分析

为验证本文避障算法在实际高空作业车结构下是否有效，对高空作业车上车臂架进行半物理实验，实验装置如图7所示。物理部分由高空作业车遥控器、遥控信号接收器、USBCAN分析仪、控制器等组成，虚拟部分由从Solidworks导入MATLAB/simscape模块的高空作业车三维物理模型以及MATLAB R2022b/Simulink中的虚拟传感器组成。半物理仿真的目的在于使用实际高空作业车的遥控器对高空车三维模型末端进行控制，验证本文避障算法能否有效避开空间障碍物，对比D-H建模计算的末端坐标以及模型直接输出的末端坐标是否存在较大误差，从而验证建模的准确性。

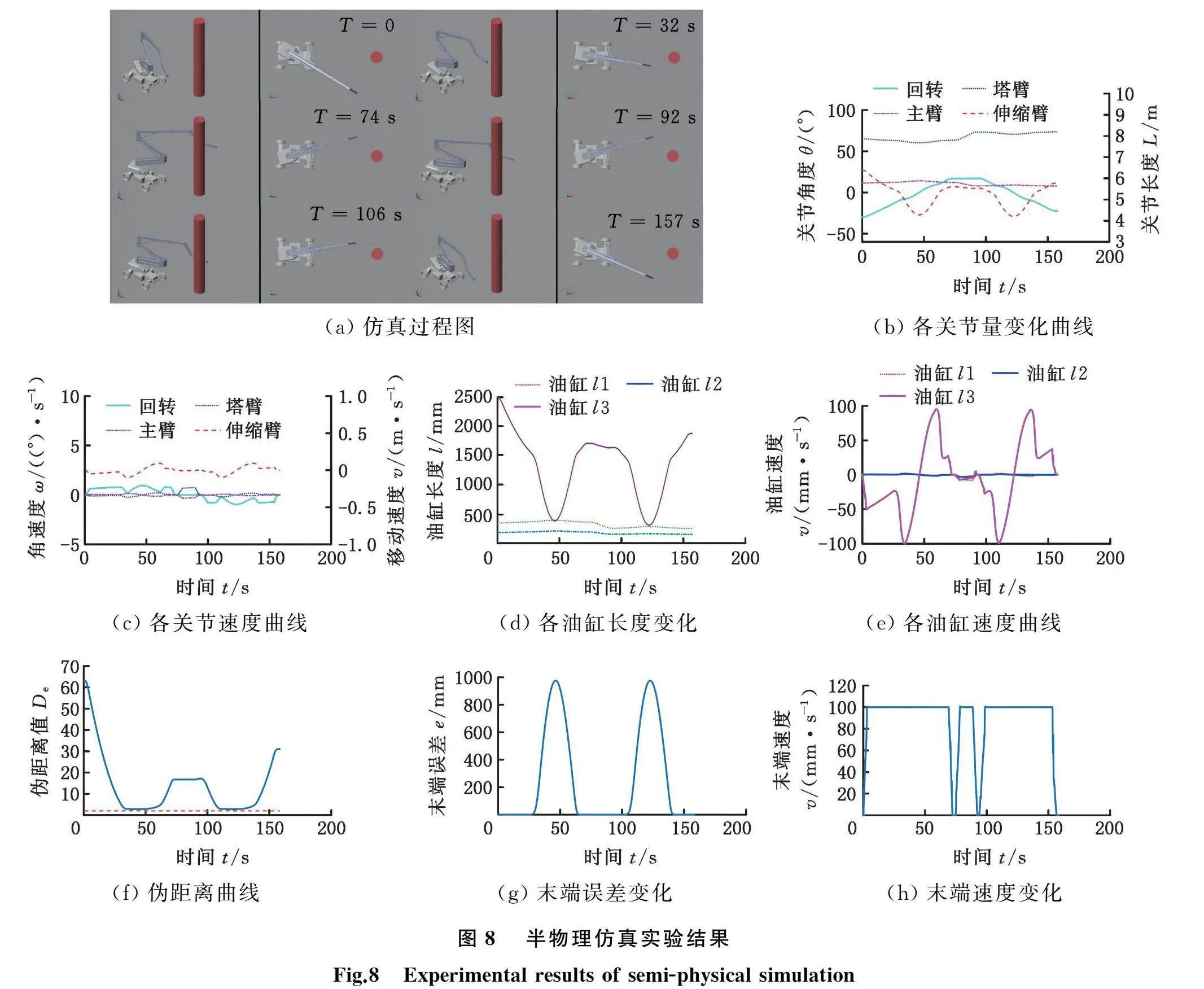
考虑到高空作业车臂架在实际应用中通过油缸驱动并通过在油缸安装的位移传感器进行闭环反馈，故在半物理仿真实验中，同样通过控制油缸位移以及油缸虚拟传感器来实现模型的驱动及闭环反馈。在控制器中通过结构几何将各关节角度换算成油缸长度，分别为塔臂油缸l1、主臂油缸l2、伸缩臂油缸l3。仿真中，设置仿真时间为160 s，回转、塔臂、主臂、伸缩臂各关节初始量为-30°、65.1287°、11.4122°、6387 mm，对应塔臂、主臂、伸缩臂的油缸伸缩量分别为339.43 mm、179.39 mm、2489 mm，障碍物中心坐标为（6941.26，0，5220.88）mm，设定速度v为100 mm/s，速度实际大小与方向通过遥控器的摇杆来控制，自适应闭环反馈Ke为20，设定阈值dm为10，绝对阈值dc为2。仿真方案如下：首先通过遥控器控制末端沿y轴正方向移动直到完成避障，用于验证程序的可行性，随后控制末端沿z轴负方向移动一段距离，最后控制末端沿y轴负方向移动进行第二次避障，验证程序对同一障碍物是否能完成多次避障，考虑到加速度与惯性的影响，通过遥控器实现末端速度的缓慢变化，仿真结果如图8所示。

由图8可以看出，为模拟实际操作，防止过大的加速度产生较大冲击，T=0时通过遥控器控制末端速度逐渐增大，到T=3 s时达到最大值100 mm/s，T=32 s时末端开始第一次避障，T=74 s时末端完成避障并且末端回到运行轨迹，在0～74 s过程中伪距离最小值为2.85，远大于绝对阈值2。T=68 s时为防止惯性加速度对臂架各关节带来较大冲击，通过遥控器控制速度逐渐减小。74～92 s时末端沿z轴负方向运动，同样通过手柄控制末端速度逐渐变化。T=94 s时末端沿y轴正方向移动进入第二次避障并在T=143 s时成功完成避障，由图8f可以看到在两次避障中，臂架第二次避障的伪距离同样大于绝对阈值;且由图8e、图8b可以看出，运行过程中各油缸的伸缩速度以及各关节量变化连续且平缓，针对不同的速度要求，可以通过修改设定速度v直接实现降低末端速度。同时，通过对比模型末端坐标与计算所得末端坐标，发现整个运行过程中末端各方向上的计算误差恒定在1 mm以内。

以上半物理仿真实验实现了对同一障碍物的多次避障并回到相应的运行轨迹，成功验证了该避障算法对于速度、最小伪距离的控制及闭环反馈的有效性，为实际工程应用提供了重要依据。

4 结论

本文针对改进梯度投影法在混合式高空作业车应用中出现的速度、轨迹不连续问题以及避障过程中的速度突变问题，提出一种基于自适应闭环反馈的高空车臂架避障运动控制算法，该算法在完成避障的基础上大大改善了高空车臂架避障过程中的速度突变，保证高空作业车运行平稳。得出结论如下：

（1）本文在改进梯度投影法的基础上进行优化，提出了一种适用于混合式高空作业车的基于加权最小范数解的二次臂架运动分配方法，实现了存在伸缩臂的高空车臂架末端的速度、轨迹连续的运动控制。

（2）采用伪距离评估臂架与障碍物的接近程度，并对避障算法进行了优化，通过设定阈值与绝对阈值的方法成功实现了对最小伪距离的控制，同时对障碍物标志点以及臂架标志点的选取方案进行优化，实现了不同情况下臂架末端正确的避障。

（3）提出一种自适应闭环反馈方法来替代传统闭环反馈方法，减少了闭环反馈在避障时对末端速度的影响，解决了避障后末端的速度突变问题。

（4）对组成末端速度的三部分（运行速度、避障速度、闭环反馈）进行速度整合，实现了对末端速度最大值以及速度突变的控制，使所提方法更适用于工程机械。

（5）进行了半物理仿真实验，成功验证了该避障算法对速度、最小伪距离的控制以及闭环反馈的有效性，为实际工程应用提供了重要依据。

参考文献：

［1］ ELIZONDO-LEAL J C， PARRA-GONZLEZ E F， RAMREZ-TORRES J G. The Exact Euclidean Distance Transform：a New Algorithm for Universal Path Planning［J］. International Journal of Advanced Robotic Systems， 2013， 10（6）：266.

［2］ SUN D， HWANG S， KIM B， et al. Creation of one Excavator as an Obstacle in C-space for Collision Avoidance during Remote Control of the Two Excavators Using Pose Sensors［J］. Remote Sensing， 2020， 12（7）：1122.

［3］ PERDEREAU V， PASSI C， DROUIN M. Real-time Control of Redundant Robotic Manipulators for Mobile Obstacle Avoidance［J］. Robotics and Autonomous Systems， 2002， 41（1）：41-59.

［4］ KHAN A H， LI Shuai， LUO Xin. Obstacle Avoidance and Tracking Control of Redundant Robotic Manipulator：an RNN-based Metaheuristic Approach［J］. IEEE Transactions on Industrial Informatics， 2020， 16（7）：4670-4680.

［5］ PARK M G， JEON J H， LEE M C. Obstacle Avoidance for Mobile Robots Using Artificial Potential Field Approach with Simulated Annealing［C］∥2001 IEEE International Symposium on Industrial Electronics Proceedings（Cat. No.01TH8570）. Pusan， 2001：1530-1535.

［6］ XU Zhihao， ZHOU Xuefeng， LI Shuai. Deep Recurrent Neural Networks Based Obstacle Avoidance Control for Redundant Manipulators［J］. Frontiers in Neurorobotics， 2019， 13：47.

［7］ JU Fengjia， JIN Hongzhe， WANG Binluan， et al. A Predictable Obstacle Avoidance Model Based on Geometric Configuration of Redundant Manipulators for Motion Planning［J］. Sensors， 2023， 23（10）：4642.

［8］ MU Zonggao， LIU Tianliang， XU Wenfu， et al. A Hybrid Obstacle-avoidance Method of Spatial Hyper-redundant Manipulators for Servicing in Confined Space［J］. Robotica， 2019， 37（6）：998-1019.

［9］ 张建华， 任宝珍， 赵岩， 等. 基于二分试探的平面冗余机械臂碰撞检测与避障［J］. 机械工程学报， 2023， 59（1）：113-122.

ZHANG Jianhua， REN Baozhen， ZHAO Yan， et al. Collision Detection and Obstacle Avoidance of Planar Redundant Manipulator Based on Dichotomous Heuristic［J］. Journal of Mechanical Engineering， 2023， 59（1）：113-122.

［10］ 国家市场监督管理总局， 国家标准化管理委员会. 高空作业车：GB/T 9465—2018［S］. 北京：中国标准出版社， 2018.

State Administration for Market Regulation， Standardization Administration of the People’s Republic of China. Vehicle-mounted Mobile Elevating Work Platform：GB/T 9465—2018［S］. Beijing：Standards Press of China， 2018.

［11］ 滕儒民， 贺浩， 项慧， 等. 基于启发式路径搜索的高空作业车避障轨迹规划［J］. 机械工程学报， 2013， 49（10）：194-198.

TENG Rumin， HE Hao， XIANG Hui， et al. Trajectory Planning with Obstacles Considered for Aerial Work Platform Based on Heuristic Path-searching［J］. Journal of Mechanical Engineering， 2013， 49（10）：194-198.

［12］ 王硕， 李恩， 赵晓光， 等. 伸缩臂高空作业车轨迹跟踪控制方法研究［J］. 华中科技大学学报（自然科学版）， 2011， 39（增刊2）：216-219.

WANG Shuo， LI En， ZHAO Xiaoguang， et al. Research on Trajectory Tracking Control Method of Aerial Work Platform with Telescopic Booms［J］. Journal of Huazhong University of Science and Technology（Natural Science Edition）， 2011， 39（S2）：216-219.

［13］ CHANG Shuai， FU Yongling， SUN Jian， et al. Inverse Kinematics Solution and Trajectory Planning of Redundant Manipulator Based on Improved Gradient Projection Method［J］. Journal of Physics：Conference Series， 2022， 2396（1）：012045.

［14］ SHI Zhong， HUANG Xuexiang， HU Tianjian， et al. Weighted Augmented Jacobian Matrix with a Variable Coefficient Method for Kinematics Mapping of Space Teleoperation Based on Human-robot Motion Similarity［J］. Advances in Space Research， 2016， 58（7）：1401-1416.

［15］ HUANG Shuihua， PENG Yonggang， WEI Wei， et al. Clamping Weighted Least-norm Method for the Manipulator Kinematic Control with Constraints［J］. International Journal of Control， 2016， 89（11）：2240-2249.

［16］ KORKMAZ O， IDER S K， OZGOREN M K. Trajectory Tracking Control of an Underactuated Underwater Vehicle Redundant Manipulator System［J］. Asian Journal of Control， 2016， 18（5）：1593-1607.

［17］ PENG Jianqing， XU Wenfu， YANG Taiwei， et al. Dynamic Modeling and Trajectory Tracking Control Method of Segmented Linkage Cable-driven Hyper-redundant Robot［J］. Nonlinear Dynamics， 2020， 101（1）：233-253.

［18］ MARCOS M D G， MACHADO J T， AZEVEDO-PERDICOLIS T P. A Multi-objective Approach for the Motion Planning of Redundant Manipulators［J］. Applied Soft Computing， 2012， 12（2）：589-599.

［19］ WAN Jun，YAO Jiafeng， ZHANG Liang’an， et al. A Weighted Gradient Projection Method for Inverse Kinematics of Redundant Manipulators Considering Multiple Performance Criteria［J］. Journal of Mechanical Engineering， 2018：，64（7/8）：475-487.

［20］ ZHANG Jianxia， ZHANG Jianxin， ZHANG Qiang， et al. Obstacle Avoidance Path Planning of Space Robot Based on Improved Particle Swarm Optimization［J］. Symmetry， 2022， 14（5）：938.

［21］ XIE Yaen， ZHANG Zhidan， WU Xiande， et al. Obstacle Avoidance and Path Planning for Multi-joint Manipulator in a Space Robot［J］. IEEE Access， 2019， 8：3511-3526.

［22］ LI Chen， YING Ma， YU Zhang， et al. Obstacle Avoidance and Multitarget Tracking of a Super Redundant Modular Manipulator Based on Bezier Curve and Particle Swarm Optimization［J］. Chinese Journal of Mechanical Engineering， 2020， 33（5）：101-119.

［23］ LIU Yong， LI Xiang， JIANG Peiyang， et al. Evolutionary Multi-objective Trajectory Optimization for a Redundant Robot in Cartesian Space Considering Obstacle Avoidance［J］. Mechanical Sciences， 2022， 13（1）：41-53.

（编辑 陈 勇）