基于位敏传感器的对中监测系统

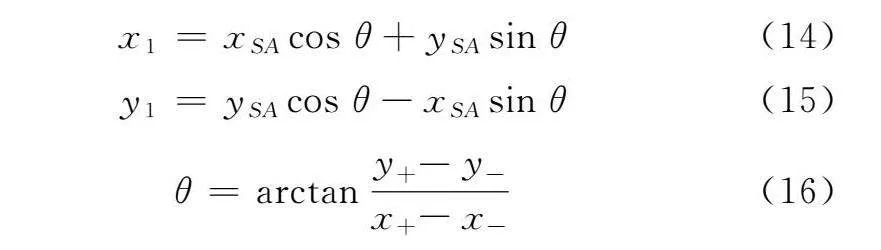
摘要：为了实时掌握柴油机动力装置的对中状态，设计了一种基于位敏传感器的对中监测系统。首先提出了基于位敏传感器的位姿变化测量方法，形成包含位姿变化的非线性方程组，通过位姿转换获得对中变化；其次通过传感器支架组件实现对方程组常量的高精度测量，通过软硬件设计形成测量系统，设计了基于简单牛顿法的复合迭代算法，保证方程组快速、准确求解；最后对测量系统的精度进行了分析，并采用四维平台进行了验证。试验结果表明：对中监测系统噪声小，偏差量噪声在0.005 mm以下，开口角噪声在0.01°以下；精度受激光入射方向影响较大，最佳入射方向下，偏差量监测精度可达0.02 mm，开口角监测精度可达0.019°。该系统将用于国产柴油机动力装置的对中监测。

关键词：船舶动力装置；位姿测量；对中监测；复合迭代算法

中图分类号：TP212.1；TH822

DOI：10.3969/j.issn.1004132X.2024.08.019

开放科学（资源服务）标识码（OSID）：

Misalignment Monitoring System Based on Position Sensitive Detector

GUO Fengze YANG Bo RONG Zhixiang YANG Junman FENG Yishuo

Power Plant Division，Shanghai Marine Diesel Engine Research Institute，Shanghai，200082

Abstract： In order to grasp the alignment status of diesel power plants in real time， a monitoring system was designed based on position sensitive detectors. Firstly， a measurement method for position and posture was proposed based on position sensitive detectors， and a nonlinear equation group incorporating position and posture was formed. By means of position and posture transformation， the alignment deviation and opening angle changes were obtained. Secondly， high-precision measurement of the constants in the equation group was achieved through the sensor bracket components. Through hardware and software design， a measurement system was formed. A composite iterative algorithm was designed to ensure fast and accurate solution of the equations based on simple Newtons method. Finally， the accuracy of the measurement system was analyzed and validated using a four-dimensional platform. The experimental results show that the monitoring system has low noise， with a deviation noise of less than 0.005 mm and an angle noise of less than 0.01°. The accuracy is greatly affected by the incident direction of the laser， with a maximum deviation measurement errors isless than 0.02 mm and a maximum opening angle measurement errors is less than of 0.019° under the best incident direction. This system will be used for monitoring the alignment status of domestic diesel power plants.

Key words： marine power plant； position and posture measurement； misalignment monitor； compound iterative algorithm

0 引言

船舶柴油机动力装置是船舶动力系统的核心组成部分，一般由柴油机、联轴器、齿轮箱（或发电机）、隔振装置等构成。动力装置运行过程中，受船体基座变形、隔振器蠕变、设备热应变、不平衡载荷等的影响，对中状态可能变差［1］，从而造成轴承/密封过早失效、联轴器寿命和传动效率降低、轴系异常振动等问题。由于船舶机舱维修条件有限，常规的巡检拆检、振动监测等方式费时费力，且难以做到及时检修，故需要更适用的方法。

对中监测指的是在动力装置正常运行时在线测量联轴器两侧设备轴心线的对中变化。对中监测技术主要有以下几种：①振动谱分析法［2］，对中偏差会引起两倍于基频的振动激励，通过分析轴振动数据可以定性分析对中质量［3］，也有通过振动数据定量计算对中偏差的研究［4］，模拟试验相对误差约10%；②应力分析法，通过应变片测量轴的应力［5］和齿轮载荷［6］，定性评价对中质量；③直接测量法，采用电涡流传感器［7］、光电传感器［8-9］、等距条纹模式法［10］直接测量轴表面相对于参考基准的距离，但由于较难选取一致的参考基准，故对两轴对中偏差的评估较为困难。此外，还有Dodd棒法［11］、轴功波动分析法［12］等方法。现有的对中在线监测技术主要停留在实验室阶段，尚未实现工程应用。

位敏传感器（position sensitive detector， PSD）是一种基于半导体横向光电效应的成熟传感器，适用于位置、姿态角等物理量的非接触、高精度、快速测量［13-14］，对中监测的本质是两轴相对位置、姿态的监测，因此位敏传感器是一种潜在适用于对中监测的传感器。高玉娥等［15］提出的基于位敏传感器的六自由度位姿测量系统可以实现两个设备相对位置和姿态的监测，理论上可以用于动力装置对中监测，但该系统的位移测量精度只有0.5 mm，角度测量精度只有0.14°，并且使用前需要现场标定。

鉴于现有对中监测技术的局限性和位敏传感器的特点，本文基于位敏传感器提出了一种新型对中变化测量方法，设计了基于该方法的对中监测系统，并进行了试验验证，为动力装置对中监测提供了一条新的技术路线。

1 系统总体方案设计

本文首先提出了基于位敏传感器的刚体位姿变化测量方法，利用该方法测量齿轮箱（或发电机）相对于柴油机的位姿变化，结合位姿转换获得动力装置的对中变化，实现对中监测。

1.1 对中变化简介

图1所示是比较典型的两种动力装置［16］，隔振装置橡胶的蠕变会比较显著地影响对中。对中变化包括偏差变化和开口变化，如图2a所示，基准法兰轴和被测法兰轴初始时基本对中，建立固结于大地的定坐标系［17］Oxyz，被测法兰轴轴心线与Ox重合，Oy为水平方向，Oz为铅垂方向。当对中状态发生变化时，图2b为偏差变化示意图，δy为水平偏差变化，δz为垂直偏差变化；图2c为开口变化示意图，OP为被测轴轴心线在Oxz平面内的投影，θy为水平开口变化，θz为垂直开口变化。

1.2 位姿变化测量原理

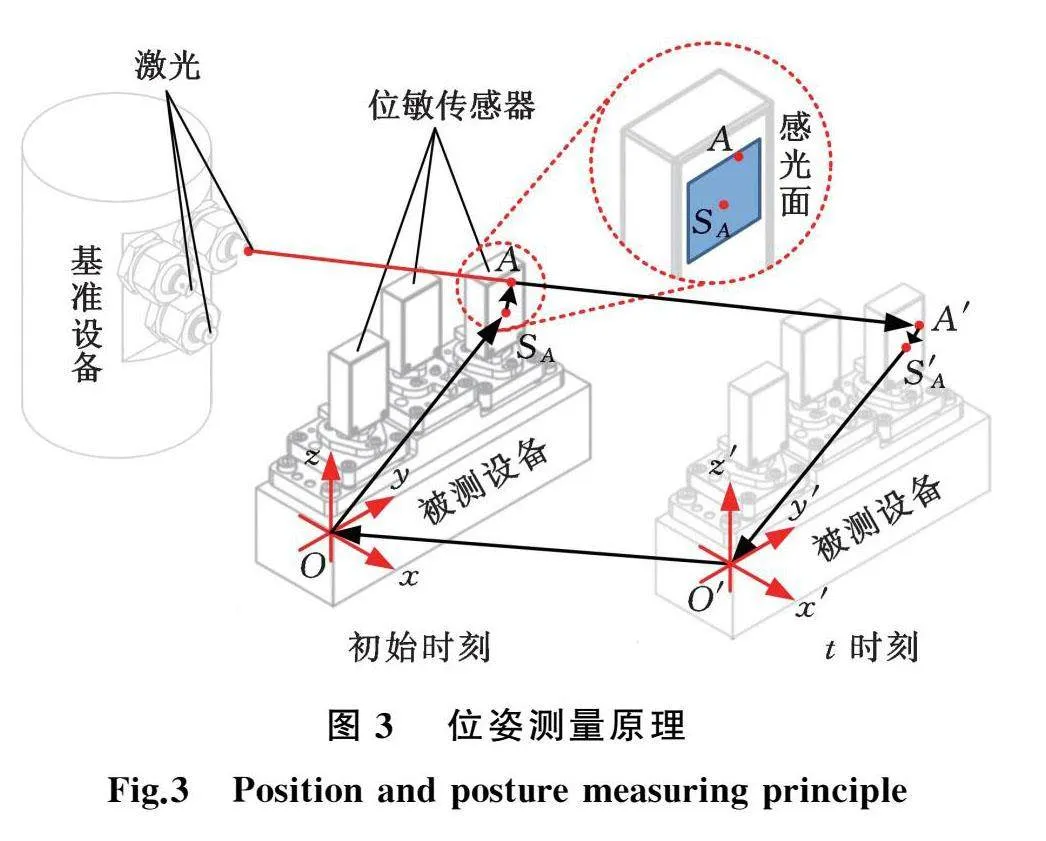
如图3所示，在基准设备上布置三组激光，在被测设备上固定三组不共线的位敏传感器，建立定坐标系Oxyz，被测设备上建立结体坐标系［17］O′x′y′z′，初始时刻结体坐标系与定坐标系重合，基准设备上的一束激光在某一传感器上形成的光斑记为A，该传感器自身坐标系的原点记为SA，经过时间t，被测设备沿Ox、Oy、Oz分别平移δx、δy、δz，绕Ox、Oy、Oz依次旋转α、β、γ后到达新位置，此时传感器原点记为S′A，形成的新光斑记为A′，根据向量关系有

OSA+SAA+AA′+A′S′A+S′AO′+O′O=0（1）

定坐标系Oxyz下，SA坐标记为SAO，S′A坐标为S′AO，光斑A坐标记为AO，光斑A′的坐标记为A′O，激光方向为LAO，存在以下关系：

AA′=c1LAO（2）

（S′AO）T=Rx（α）Ry（β）Rz（γ）STAO+［δxδyδz］T（3）

Rx（α）=1000cos α－sin α0sin αcos α

Ry（β）=cos β0sin β010－sin β0cos β

Rz（γ）=cos γ－sin γ0sin γcos γ0001

式中，c1为光矢量沿激光方向增加的倍数。

定坐标系Oxyz下，光斑A′坐标为A′O，O′坐标为O′O，存在以下关系：

（A′O）T=Rx（α）Ry（β）Rz（γ）（A′O′）T+［δxδyδz］T（4）

O′O=［δxδyδz］（5）

将式（2）～式（5）代入式（1），整理得

ATO+c1LTAO+Rx（α）Ry（β）Rz（γ）（A′O′）T+

［δxδyδz］T=0（6）

综合三组激光和传感器有

ATO+c1LTAO+Rx（α）Ry（β）Rz（γ）（A′O′）T+

［δxδyδz］T=0

BTO+c2LTBO+Rx（α）Ry（β）Rz（γ）（B′O′）T+

［δxδyδz］T=0

CTO+c3LTCO+Rx（α）Ry（β）Rz（γ）（C′O′）T+

［δxδyδz］T=0（7）

式（7）是一个非线性方程组，包含以下9个变量：平移量δx、δy、δz，旋转角α、β、γ以及位姿变化前后光矢量沿激光方向增加的倍数c1、c2、c3。求解式（7），并将结果代入式（3）即可得到S′AO、S′BO、S′CO，进而确定t时刻被测设备在定坐标系下的位姿。船舶动力装置更关注设备相对于自身初始状态的变化，即δx、δy、δz、α、β、γ，故直接求解式（7）即可。

1.3 位姿变化向对中变化转换

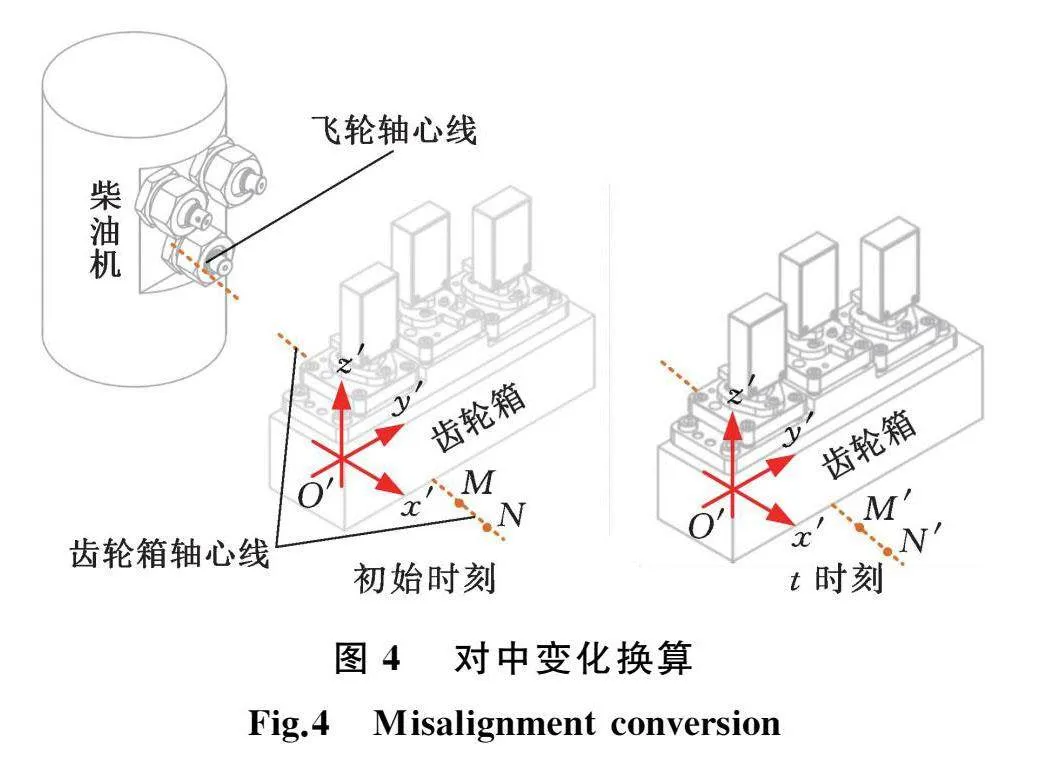
对中变化通过轴心线的位姿变化体现。假设基准设备为柴油机，被测设备为齿轮箱，柴油机飞轮轴心线和齿轮箱轴心线如图4所示。齿轮箱基于结体坐标系O′x′y′z′的位姿变化为（δx，δy，δz，α，β，γ），M、N是固定在齿轮箱轴心线上的两点，初始测得M、N在结体坐标系下的坐标分别为M=（xm，ym，zm）、N=（xn，yn，zn），t时刻在定坐标系下的坐标值分别为M′=（x′m，y′m，z′m）、N′=（x′n，y′n，z′n），则

MT=Rx（α）Ry（β）Rz（γ）（M′）T+［δxδyδz］T（8）

NT=Rx（α）Ry（β）Rz（γ）（N′）T+［δxδyδz］T（9）

基于轴心线上点M的对中变化如下：齿轮箱沿Oy、Oz方向偏差变化为δOy、δOz，绕Oy、Oz轴的开口变化为θOy、θOz。如果Oy为水平方向，Oz为重力方向，则δOy、δOz和θOy、θOz依次为水平偏差变化、垂直偏差变化和水平开口变化、垂直开口变化，有

δOy=y′m－ym（10）

δOz=z′m－zm（11）

θOy=

arctanz′m－zm［（xm-xn）2+（ym-yn）2+（zm-zn）2］1/2（12）

θOz=

arctany′m-ym［（xm-xn）2+（ym-yn）2+（zm-zn）2］1/2（13）

1.4 方程组常量的测量

为了求解式（7），首先需要测量方程组中的常量，方程组常量如下：初始时刻激光在定坐标系下的方向LAO、LBO和LCO，初始时刻光斑在定坐标系下的坐标AO、BO和CO，t时刻新光斑在结体坐标系下的坐标A′O′、B′O′和C′O′，以及轴心线上两点M、N在结体坐标系下的坐标值。

1.4.1 传感器原点坐标

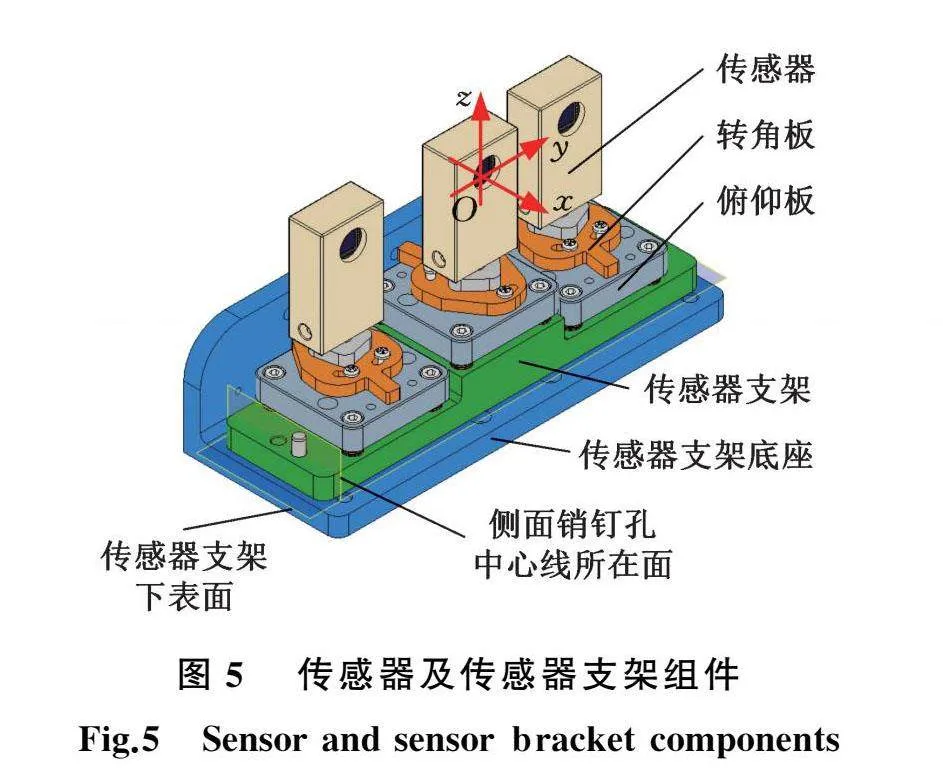
光斑坐标由传感器原点坐标、传感器输出的光斑坐标、传感器位姿计算而来，因此首先测量传感器原点坐标。设计图5所示传感器支架组件，传感器支架组件由转角调整板、倾角调整板、传感器支架、传感器支架底座构成，侧面设计有两组四个销钉孔，建立定坐标系Oxyz（右手系）如下：O点位于中间传感器自身坐标系原点，Ox平行于侧面销钉孔中心线所在面，Oz垂直于传感器支架下表面。

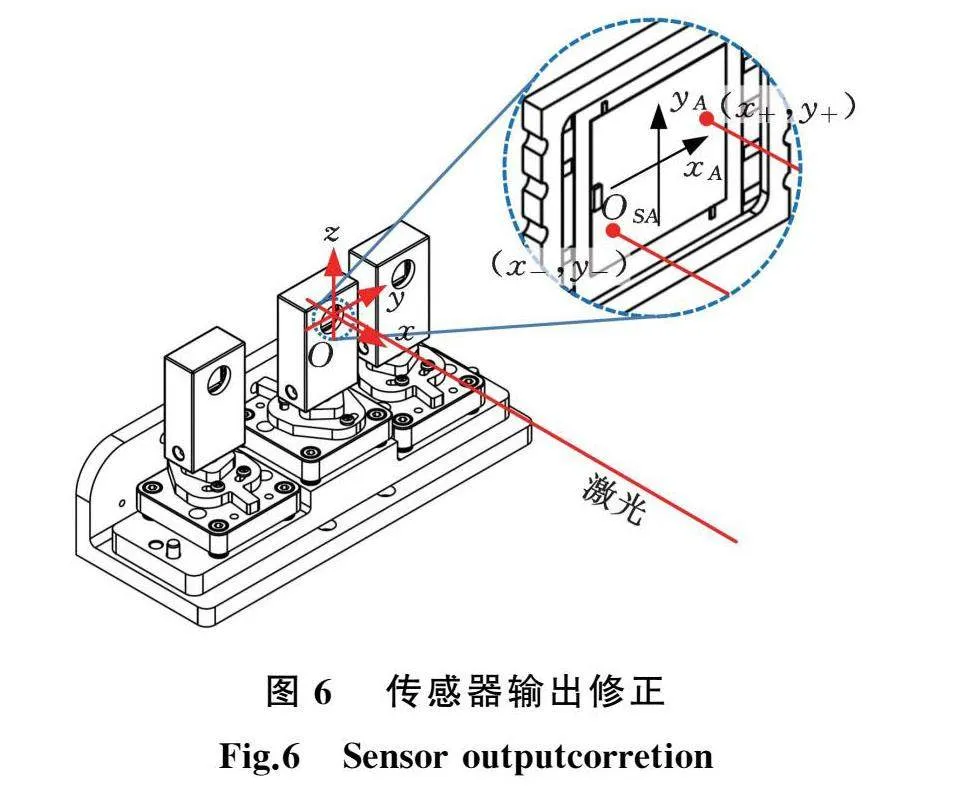
通过调整转角板、俯仰板使三组传感器的感光面平行于Oyz平面。由于传感器自身坐标系与Oy、Oz方向不一致，对传感器输出进行以下修正：如图6所示，（OSAxAyA为传感器自身坐标系，O和OSA重合），采用一束平行于Ox方向的激光，沿Oy方向平移激光，在传感器两个极限量程位置下，传感器的输出分别为（x-，y-）、（x+，y+），如图7所示，则有

x1=xSAcos θ+ySAsin θ（14）

y1=ySAcos θ－xSAsin θ（15）

θ=arctany+－y－x+－x－（16）

式中，xSA、ySA为传感器输出的光斑坐标；θ为OSAxA和Oy夹角；x1、y1为修正后的光斑坐标。

通过沿Oy、Oz方向平移激光测量三组传感器原点在Oy、Oz方向间距，利用激光测距仪测量Ox方向间距，获得三组传感器原点在Oxyz下的坐标：

SAO=（xAO，yAO，zAO）

SBO=（0，0，0）

SCO=（xCO，yCO，zCO）（17）

1.4.2 激光方向

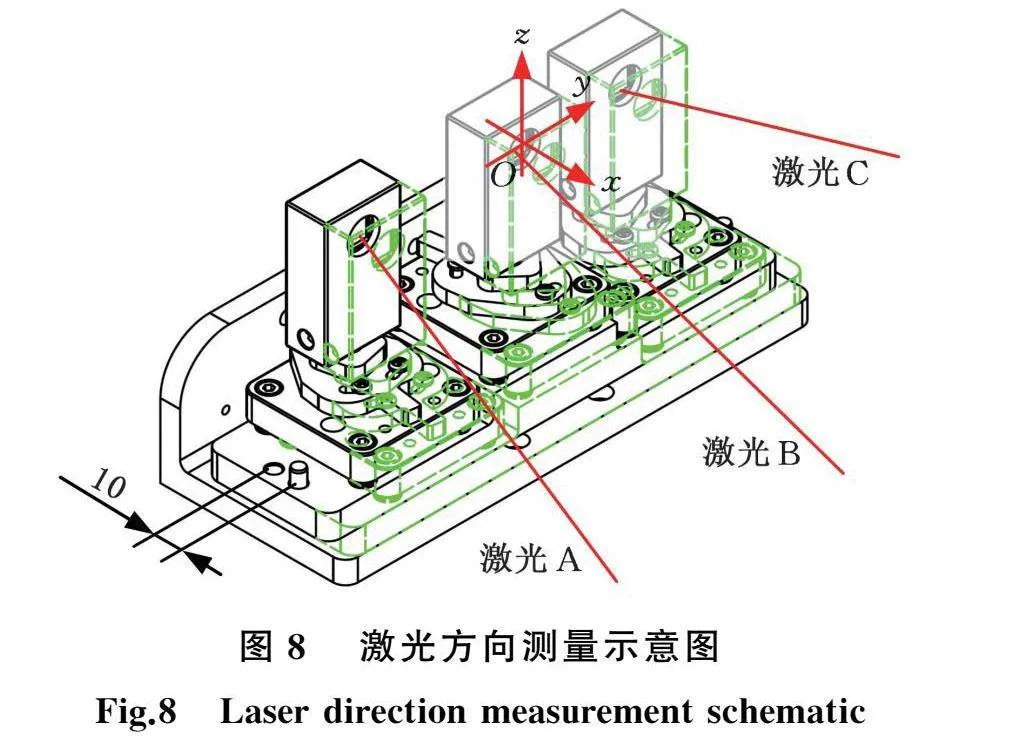
利用传感器自身较高的光斑识别精度，如图8所示，借助销钉将传感器沿Ox方向平移10 mm，平移前三组传感器输出经修正为（xA0， yA0）、（xB0， yB0）、（xC0， yC0），平移后传感器的输出经修正为（xAT， yAT）、（xBT， yBT）、（xCT， yCT），以平移后的状态为初始时刻建立结体坐标系，则激光方向如下：

LAO=（10 mm，xA0－xAT，yA0－yAT）

LBO=（10 mm，xB0－xBT，yB0－yBT）

LCO=（10 mm，xC0－xCT，yC0－yCT）（18）

1.4.3 初始时刻、t时刻光斑坐标及轴心线上两点坐标

由于修正后的传感器坐标方向与Oy、Oz方向一致，故初始光斑坐标为

AO=（xAO，yAO+xAT，zAO+yAT）

BO=（0，xBT，yBT）

CO=（xCO，yCO+xCT，zCO+yCT）（19）

t时刻，修正后的传感器输出为（xAt，yAt）、（xBt，yBt）、（xCt，yCt），结体坐标系下的光斑坐标为

A′O′=（xAO，yAO+xAt，zAO+yAt）

B′O′=（0，xBt，yBt）

C′O′=（xCO，yCO+xCt，zCO+yCt）（20）

轴心线上两点M、N在结体坐标系下的坐标值在测量系统安装后现场测量。

1.5 对中监测系统设计

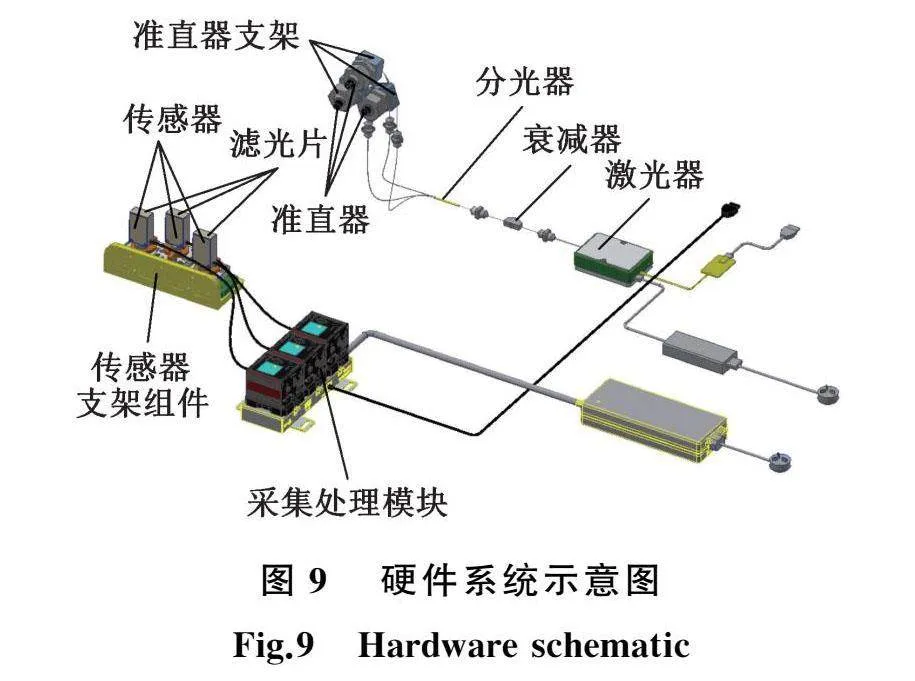
对中监测系统的硬件包括激光器、衰减器、分光器、准直器支架、准直器、滤光片、传感器、传感器支架组件、采集处理模块等，如图9所示。激光器采用半导体激光器，中心波长660 nm，带宽5 nm，光功率0.5～1 mW范围内可调；位敏传感器采用基于硅光电二极管的枕形网格横向传感器，感光面有效面积9 mm×9 mm，光斑重心识别精度1 μm，可识别激光波长范围320～1120 nm。

由于滤光片存在“蓝移现象”［18］，故滤光片选型应考虑入射角的影响。在相对较小的入射角下，滤光片中心波长与入射角的关系如下：

λθ=λ01－（n0neffsin θ）2（21）

式中，λθ为入射角为θ时滤光片的中心波长，nm；λ0为垂直入射到滤光片时的中心波长，nm；n0为介质的折射率；neff为滤光片有效折射率；θ为入射角，（°）。

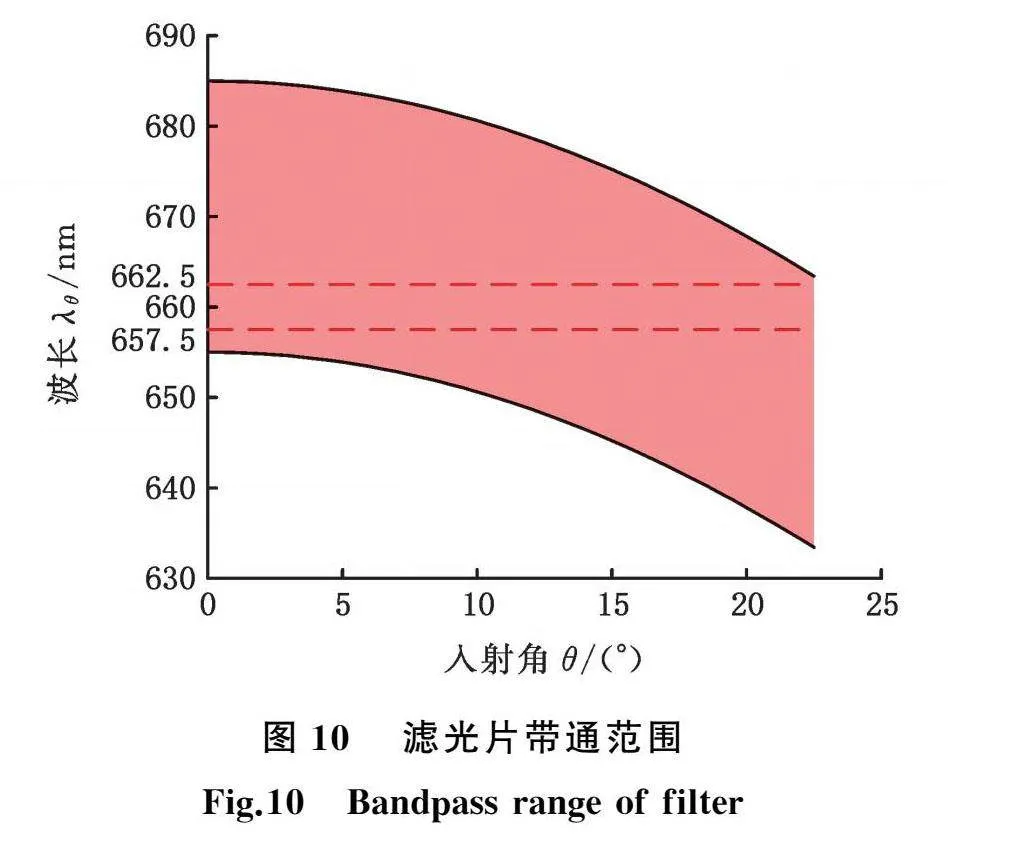
最终滤光器中心波长670 nm，半带宽15 nm（材料为K9玻璃，对660 nm的光波折射率为1.52），图10所示为不同入射角下滤光片的带通范围，要求激光入射角不能超过22.5°。

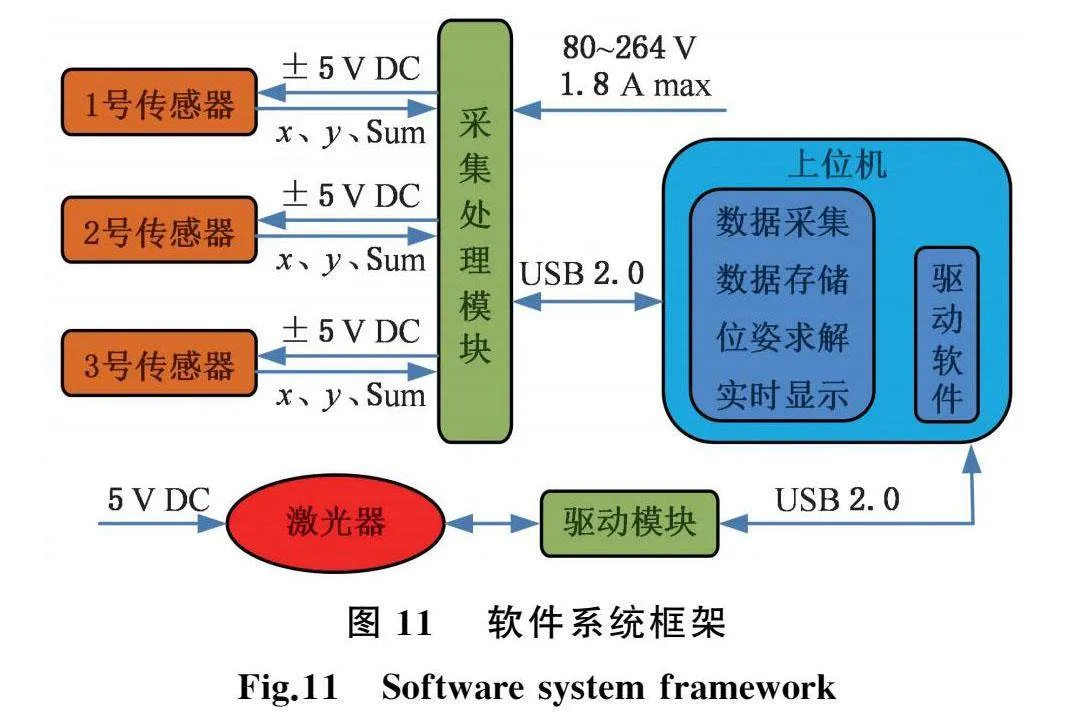
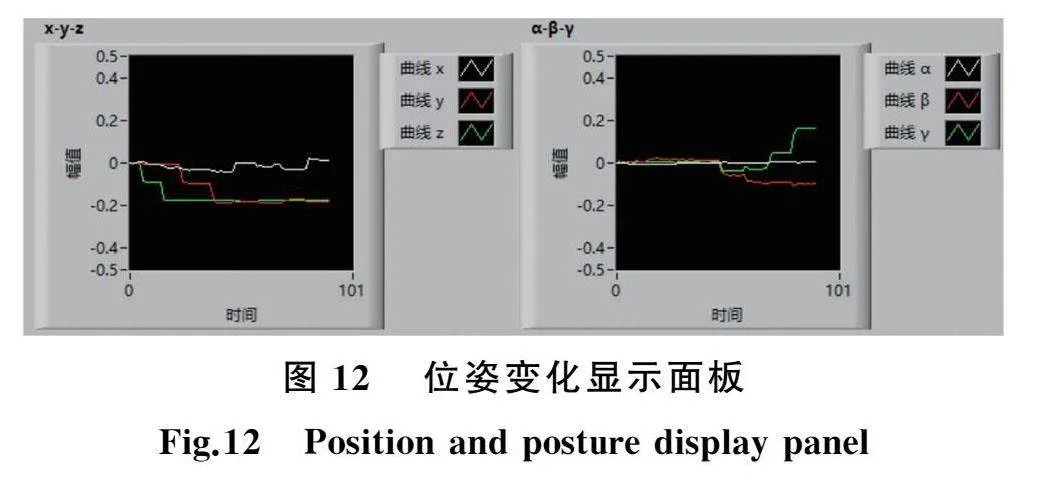
根据硬件系统、复合迭代算法以及位姿变化向对中变化的换算，基于Labview开发了测量软件，软件系统框图见图11，可以实现对传感器数据的采集、存储以及对中变化的求解和实时显示，图12所示为对中变化显示面板。

2 复合迭代算法

式（7）是一个高维非线性方程组，若采用一般的迭代法容易陷入局部重根甚至不收敛，故需要制定适用的算法。

2.1 传感器数据模拟

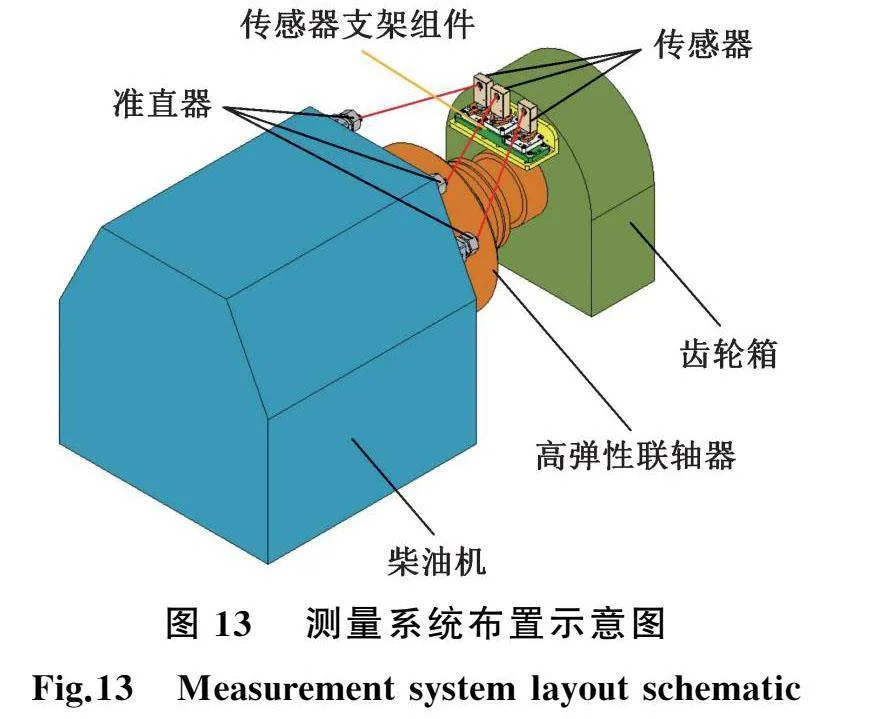
首先模拟传感器数据，用于算法评估和验证。考虑到机组振动，假设齿轮箱相对于柴油机的位姿变化量可表示为时均值叠加波动值，时均值为稳定常数，波动值为振动引起的位姿变化波动。布置测量系统如图13所示，假设位姿变化满足：

（δx，δy，δz，α，β，γ）=（－0.120 mm，0.210 mm，

0.530 mm，－0.100°，0.500°，－0.300°）+

（0.5sin（628t）mm，0.283sin（628t）mm，

0.283sin（628t）mm，0，0，0）（22）

通过坐标转换获得传感器输出数据，如图14所示。

2.2 牛顿迭代法的局限性

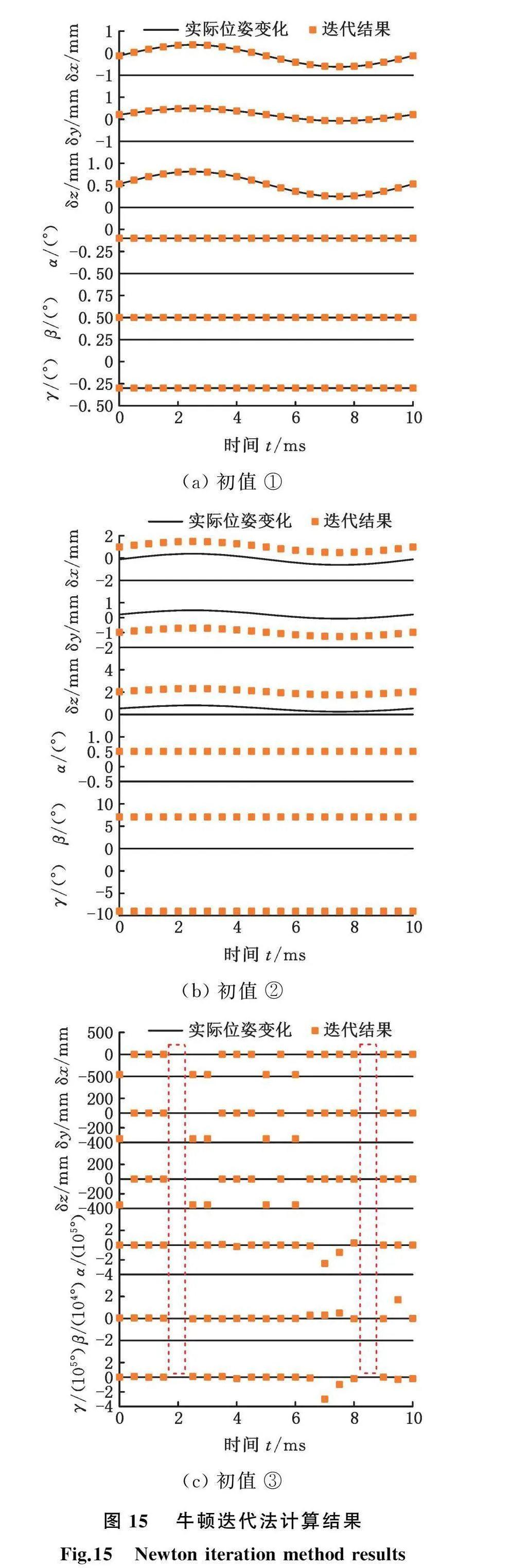
牛顿迭代法是最经典的非线性方程组求解算法，其理念是将方程组的非线性项逐次线性化，从而获得迭代循环过程［19］。采用牛顿迭代法对图14中一个周期（0～10ms）内的位姿变化进行计算（典型配置：Core i7处理器，16 GB内存，MATLAB 2014），迭代初值见表1。

图15所示为牛顿迭代法的计算结果，图15a采用初值①作为迭代初值，在所有时刻均获得了收敛解，且收敛解与实际位姿变化完全符合，计算共耗时10.48 s；图15b采用初值②作为迭代初值，在所有时刻也获得了收敛解，但收敛解与实际位姿变化相差甚远，这是因为采用初值②时迭代循环收敛到方程组其他的根，即式（7）实际是存在重根的，计算共耗时13.32 s；图15c采用初值③作为迭代初值，在部分时刻获得了收敛解，但只收敛到了方程组的其他根，同时采用初值③时，迭代循环的收敛性变差，在t=2 ms和t=8.5 ms时并未收敛，计算耗时显著增加，共耗时73.92 s。

对于式（7）的求解，牛顿迭代法存在以下局限性：①平均每个收敛点计算耗时约0.7 s，耗时较长；②式（7）在绝大多数情况下具有重根，采用牛顿迭代算法很难保证得到的收敛解是实际的位姿变化；③算法对迭代初值比较敏感，不合适的初值会严重影响收敛性和收敛速度。

2.3 复合迭代算法

针对牛顿迭代法的上述局限性，为了快速、正确地获得位姿变化数据，本文提出了基于简单牛顿法的复合迭代算法，其核心思想如下：针对连续变化的位姿，两个相邻时间点的位姿变化充分接近，故式（7）可以用上一个时间点的计算结果作为初值，进行迭代计算。则式（7）的求解算法可分为两部分：第一部分针对首个时间点，求解算法侧重收敛性和合理性；第二部分针对后续时间点，求解算法侧重收敛速度。

复合迭代算法流程如图16所示，首个时刻对方程组在合理区域内所有的根进行搜索，并判定所获得的根是否为实际位姿变化；后续时刻以上一时刻的计算结果为初值，采用简单牛顿法迭代求解。

合理区域需要根据具体问题确定，对于动力装置（图13），根据机组运行经验，该区域可表示为Ω={δx，δy，δz，α，β，γ|δx∈（-6，6）mm，δy∈（-12，12）mm，δz∈（-12，12）mm，α∈（-5°，5°），β∈（-1°，1°），γ∈（-1°，1°）}。

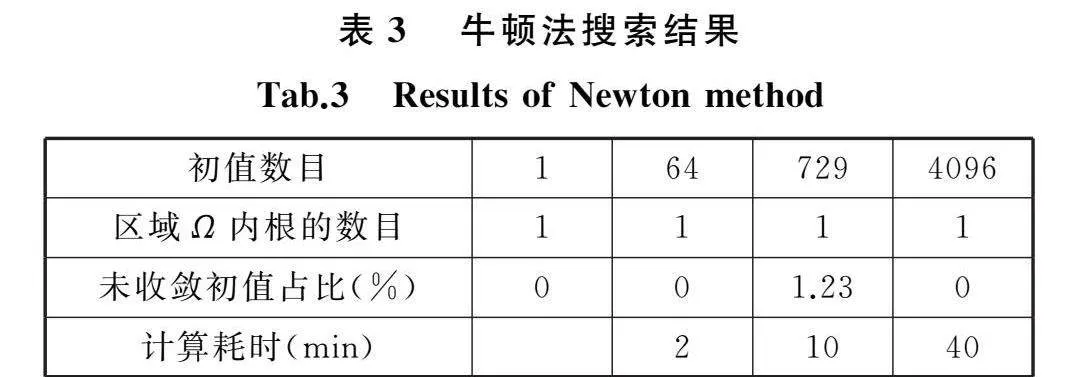
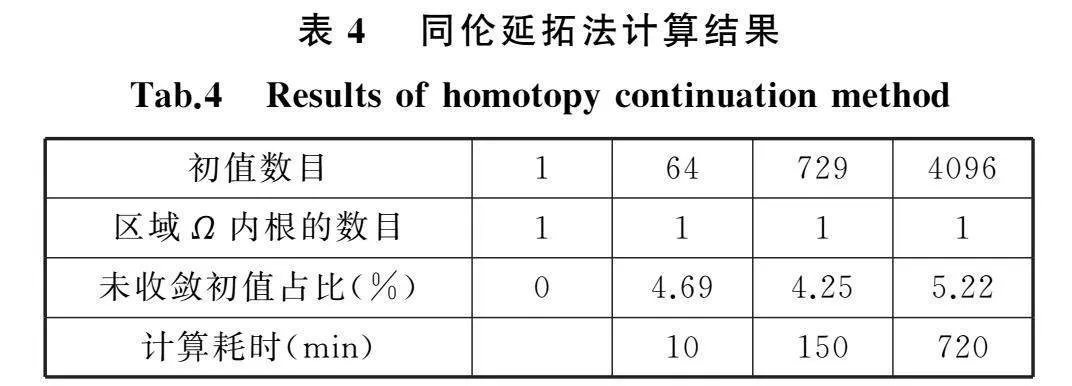
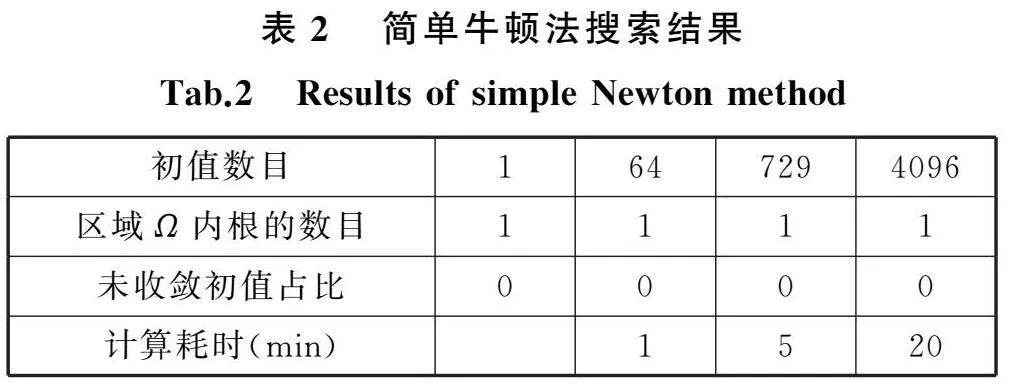
式（7）是典型的高维非线性方程组，高维非线性方程组在特定区域内所有根的搜索是非常困难的，目前主流方法是大范围收敛算法，并投入足够多的迭代初值，对所有根进行追踪［20］。本文在区域Ω均匀选取1、64、729、4096组初值，通过简单牛顿法［19］、牛顿法［19］、同伦延拓法［19］对式（7）在区域Ω内的根进行搜索，计算结果见表2～表4，采用1、64、729、4096组初值和三组算法均在区域Ω内获得了唯一根，且与实际位姿变化一致。

三组算法中，同伦延拓法虽然理论上具有较大的收敛范围［21］，但对式（7）并未表现出良好的收敛性，在4%～5%的初值下，算法未收敛，且计算耗时最长；多组初值下，简单牛顿法均获得了收敛解，并且计算耗时最短。

综上，通过在区域Ω内均布64组初值，采用简单牛顿法可实现式（7）在区域Ω内所有根的搜索。所获得的根是实际位姿变化的判定方法如下：式（7）在区域Ω内有唯一根，则该唯一根是实际的位姿变化；否则，增加迭代初值数目或重新调整区域Ω。

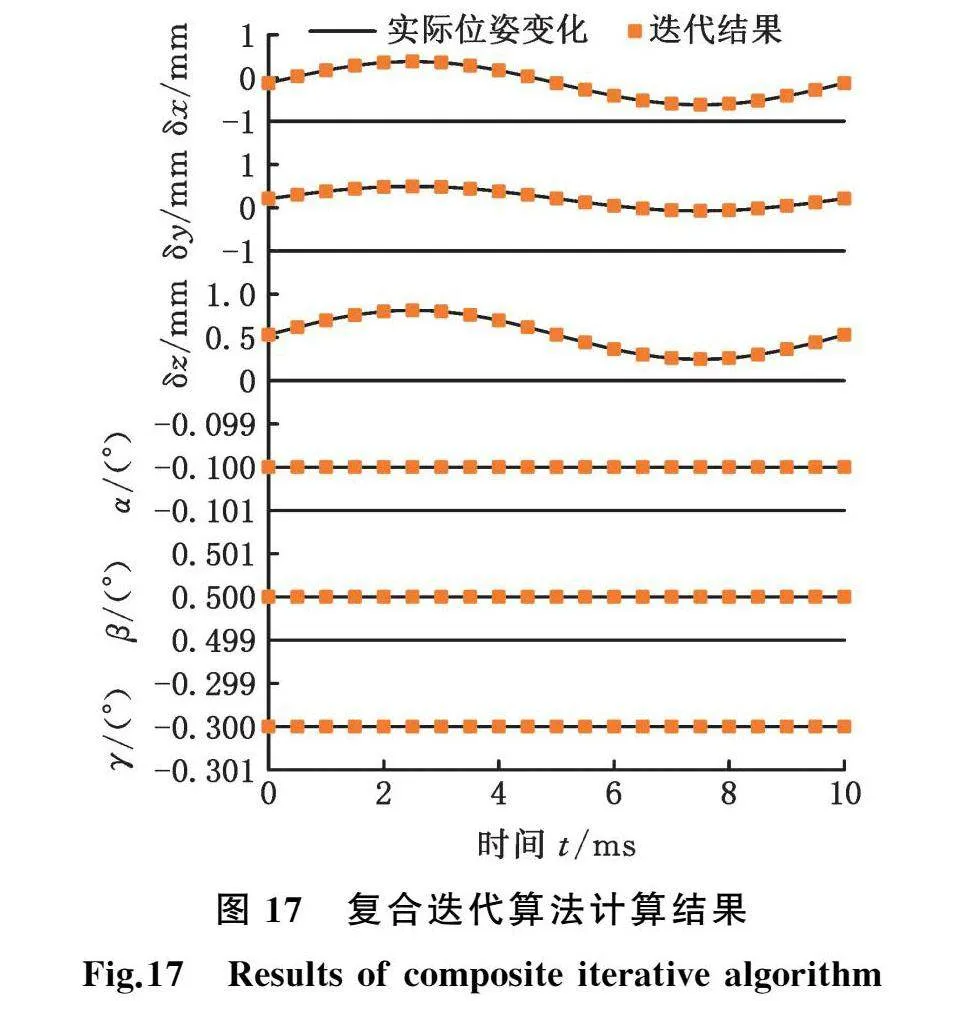
采用复合迭代算法对图14中一个周期（0～10 ms）内的位姿变化进行计算，结果如图17所示，每个时刻的计算误差不大于0.1%，计算耗时不多于0.08 s。复合迭代算法可以保证计算结果的准确性，计算耗时约为牛顿迭代法的1/9。

3 误差分析

3.1 误差来源

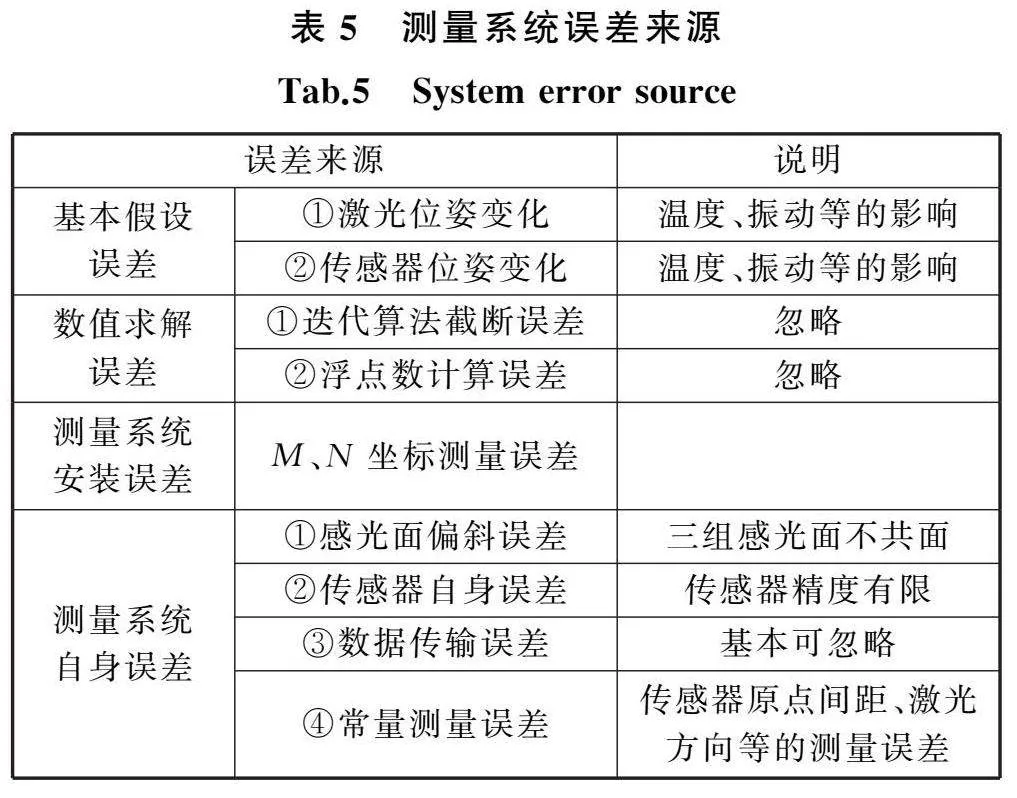
测量系统基本假设如下：激光束为准直光束，激光束相对于柴油机轴心线的位姿不变，传感器相对于齿轮箱轴心线的位姿不变。当满足基本假设，测量系统安装时M、N点可精确测量，且式（7）中的常量准确、方程组可精确求解时，测量系统误差基本为0。据此分解出4方面误差来源，见表5。

3.2 误差评估

基本假设误差是不可避免的，特别是温度变化引起的变形。图18所示为温度由20 ℃提高至30 ℃时传感器的热变形，由于传感器对外安装点与感光面平齐，感光面基本只有沿z轴的位移（约4.5 μm），温度变化控制在2 ℃内，则可控制温度引起的光斑位移在0～1 μm。传感器安装点到轴心线的位移则需要根据不同温度下的变形进行修正。

数值求解误差与式（7）的求解算法相关，如果采用迭代法求解，则取决于算法截断误差和浮点数计算误差，基本可以忽略。

测量系统安装误差取决于轴心线上M、N点的测量精度，假设M、N点测量误差不大于5 mm（M、N间距不小于300 mm）。

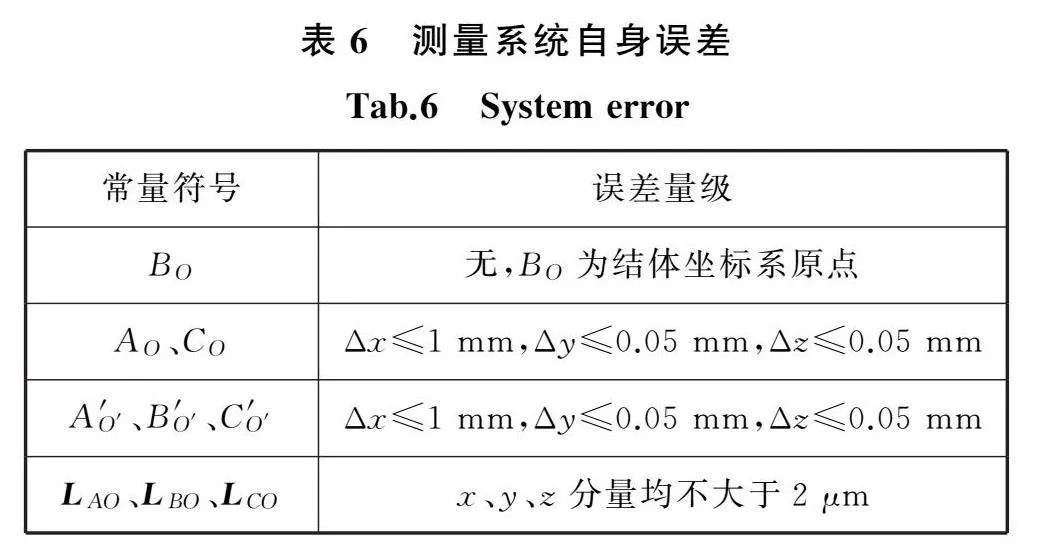
测量系统自身误差主要影响初始时刻传感器原点坐标、激光方向精度，取决于传感器支架组件加工精度以及原点坐标、激光方向测量方法，根据本文的测量系统和测量方法，预计测量系统自身误差见表6。

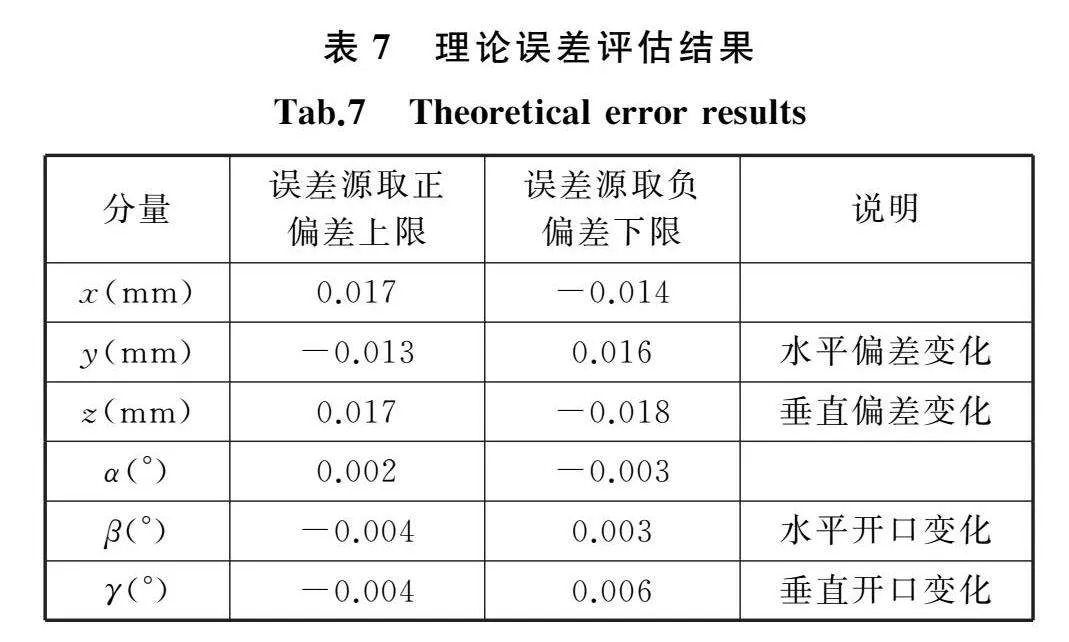
采用图13的三维模型，利用建模软件模拟出δx∈（-0.5，0.5）mm，δy，δz∈（-0.2，0.2）mm，α∈（-0.1°，0.1°），β，γ∈（-0.2°，0.2°）的位姿变化，将建模软件中的理论光斑坐标、理论常量等代入式（7）、式（8）～式（13），同时代入基本假设误差、测量系统安装误差、测量系统自身误差，求解

方程组获得4方面误差共同作用下的测量结果，极限误差下的误差评估结果见表7，预计样机偏差变化测量精度可达0.02 mm，开口变化测量精度可达0.01°。

4 试验方案

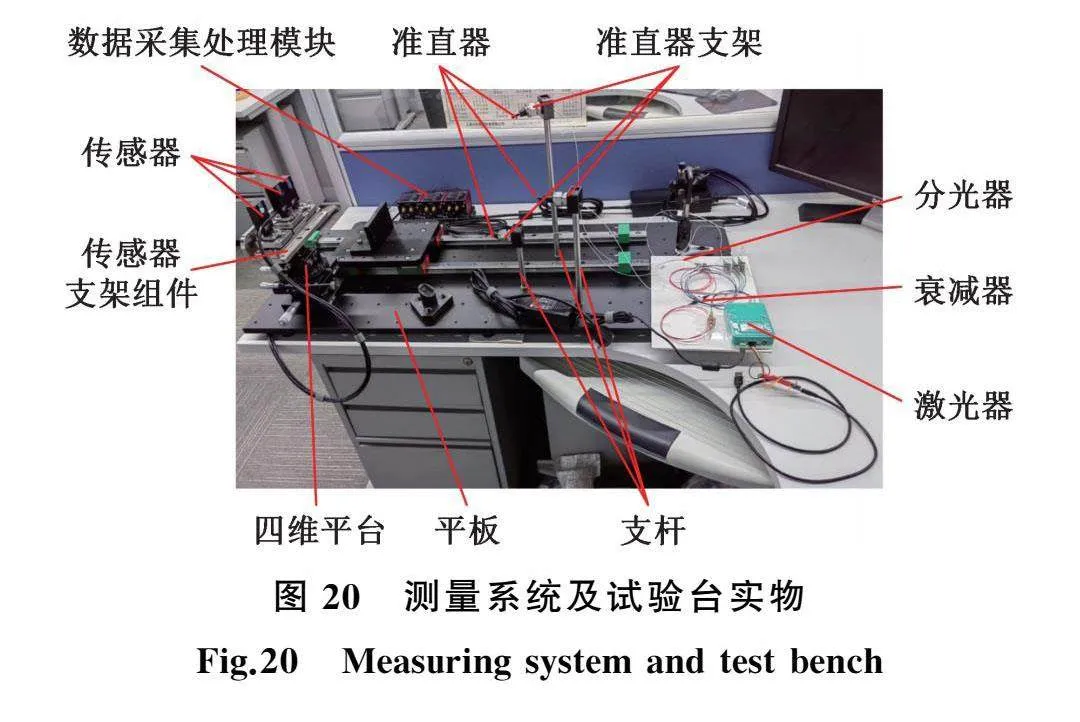
图19为试验台示意图，试验台由平板、支杆（100 mm、200 mm、300 mm三种长度规格）、四维平台等构成，四维平台由升降台、角位台、旋转台、平移台构成，可以模拟水平、垂直偏差变化（精度均为0.01 mm）和水平、垂直开口变化（精度分别为24″和34″）。传感器固定在四维平台上表面，准直器通过支杆固定在平板上，准直器出射激光投向传感器感光面。虚拟齿轮箱轴心线由四维平台的角位台和旋转台的回转中心线确定，手动调整四维平台可使传感器随着虚拟齿轮箱轴心线平移或旋转，从而产生对中变化，传感器内光斑相应发生移动。准直器通过支杆固定在平板上，改变支杆的安装位置和高度可以调整激光进入传感器感光面的入射角，从而评估入射角对测量精度的影响。测量系统及试验台实物如图20所示。

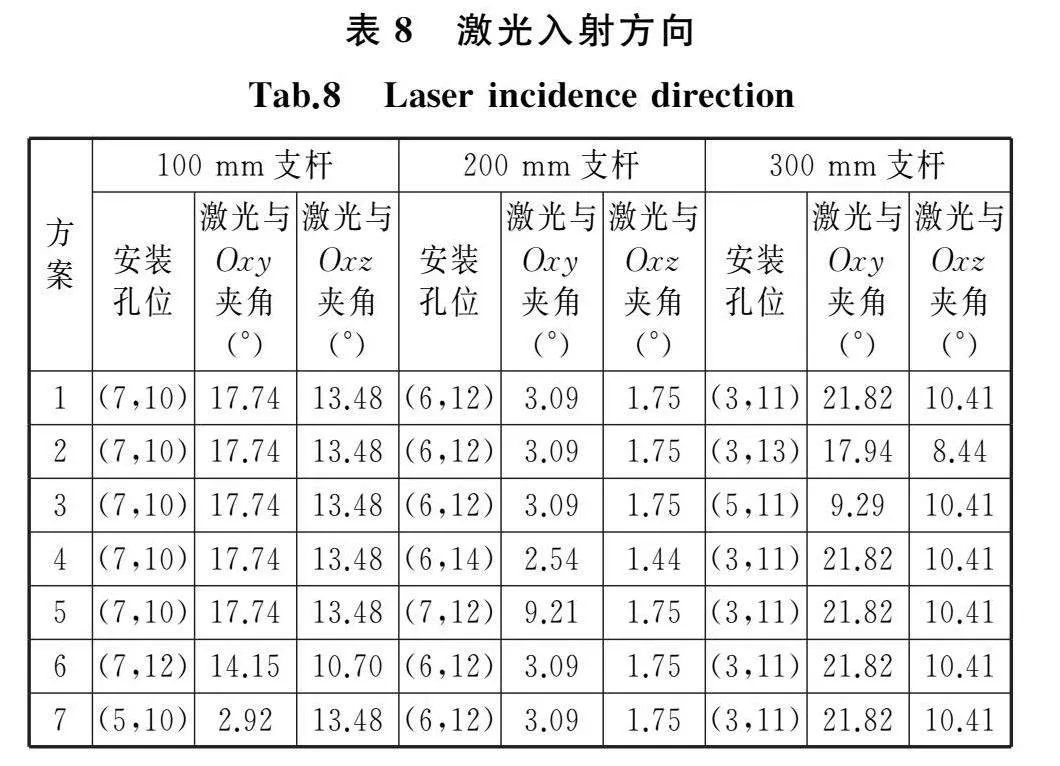
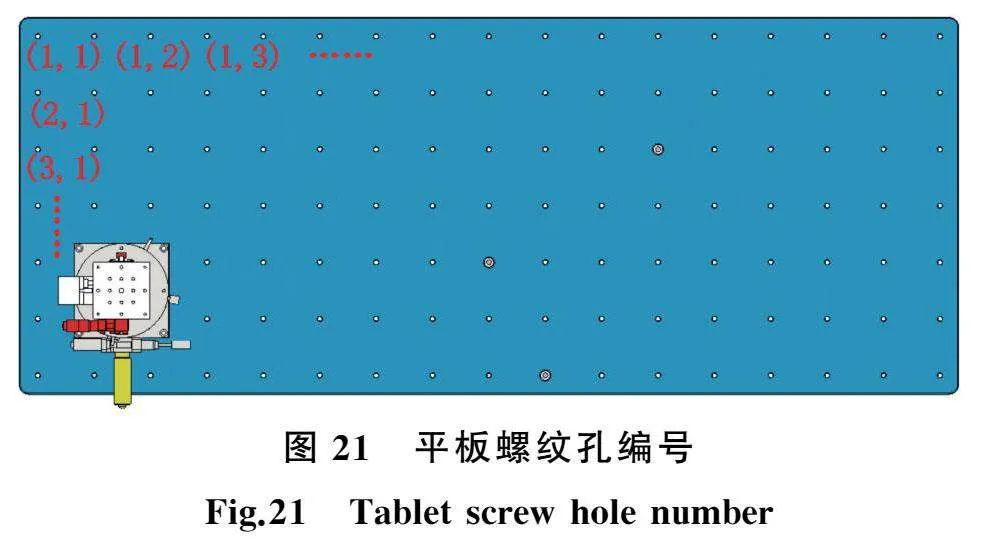
试验主要考查测量系统的精度以及激光入射方向对精度的影响。通过移动准直器支架的位置获得不同的入射方向，如图21所示，从光学平板左上角起，第一排第一个螺纹孔记为（1，1）号孔位，第一排第二个孔位记为（1，2）号孔位，依次类推。如表8所示，将支杆安装在平板的不同孔位上，形成7种试验方案，对应7种入射方向。

5 试验结果

5.1 噪声分析

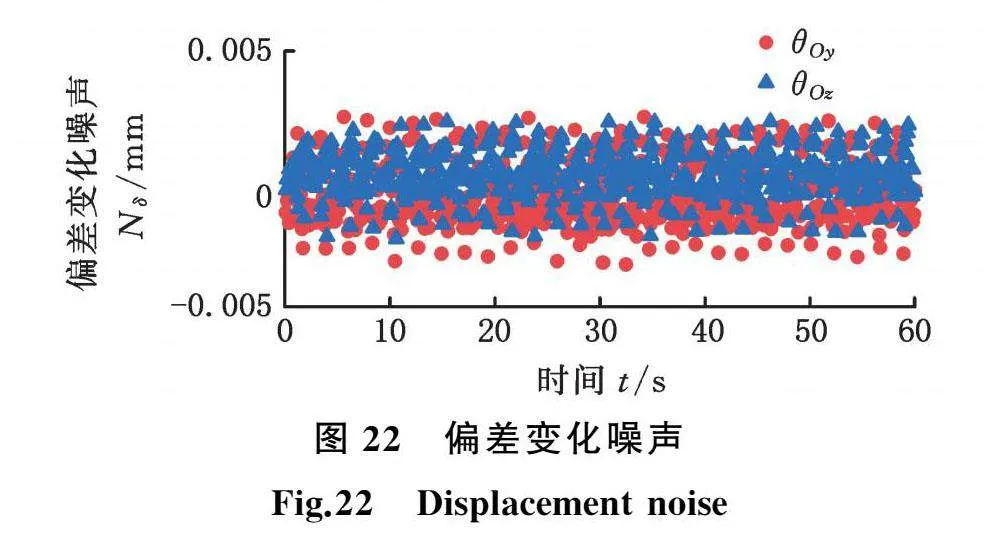
图22和图23所示为静止时测量系统输出的对中变化，表征了噪声水平。受背景光、传感器电路、浮点运算等的影响，系统存在一定噪声，可以看出，测量系统的偏差变化噪声在0.005 mm以下，开口变化噪声在0.01°以下。

5.2 精度分析

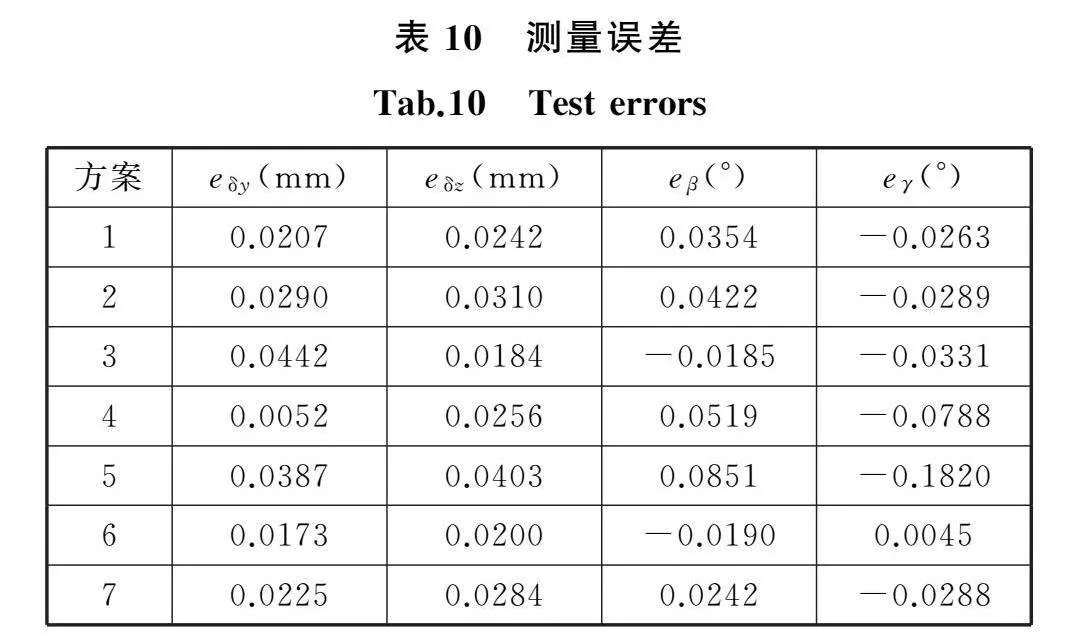
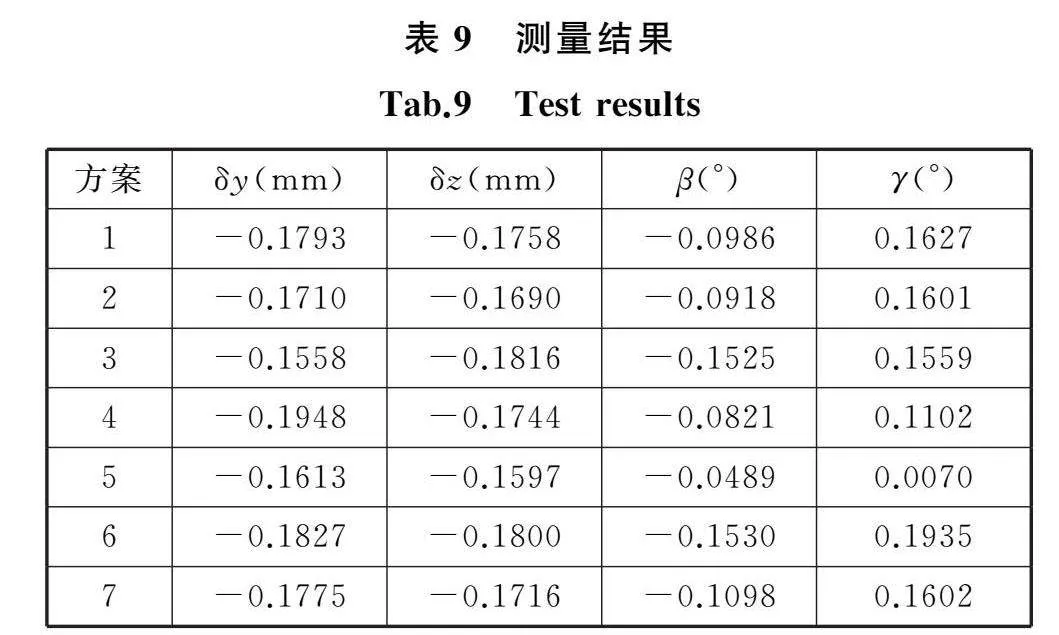
依次对表8中的激光入射方向进行测试，利用四维平台模拟产生（δOy，δOz，θOy，θOz）=（-0.200 mm，-0.200 mm，-0.134°，0.189°）的对中变化，测量结果和误差见表9、表10。

大部分试验方案下，监测系统对偏差变化的测量误差在0.03 mm以内，对开口变化的测量误差在0.05°以内；其中试验方案6和7获得了良好的精度，尤其是方案6，偏差变化的测量误差低至0.017 mm和0.02 mm，开口变化的测量误差低至0.019°和0.005°。

理论预计的样机偏差变化0.02 mm，开口变化0.01°，两者之间的差异可能与以下3方面有关：①样机零部件加工误差；②四维平台自身误差；③激光稳定性的影响。

6 结论

（1）本文提出的基于位敏传感器的对中监测系统可以实现对中变化的连续、高精度测量。

（2）受背景光、传感器电路等的影响，测量系统存在噪声，偏差量噪声在0.005 mm以下，开口角噪声在0.01°以下。

（3）测量系统受激光入射方向的影响较大，大部分入射方向下，偏差变化测量误差不大于0.03 mm，开口变化测量误差不大于0.05°，通过调整激光入射方向，最高可以实现0.02 mm的偏差变化测量精度和0.019°的开口变化测量精度。

参考文献：

［1］ 蒋平. 多因素综合效应下大型船舶轴系校中研究［D］. 武汉：武汉理工大学， 2012.

JIANG Ping. Research on Shafting Alignment of Large Ships under Multi-factor Comprehensive Effect［D］. Wuhan：Wuhan University of Technology， 2012.

［2］ 陈凯. 基于变分模态分解的舶舶轴系状态监测及故障诊断方法研究［D］. 武汉：武汉理工大学， 2018.

CHEN Kai. Research on Condition Monitoring and Fault Diagnosis Method of Marine Shafting Based on Variational Modal Decomposition［D］. Wuhan：Wuhan University of Technology， 2018.

［3］ 陈宏， 雷文平， 陈磊， 等. 一种转子动态不对中量计算方法［J］. 中国机械工程， 2016， 27（17）：2379-2383.

CHEN Hong， LEI Wenping， CHEN Lei， et al. A Novel Quantitive Calculation Method of Dynamic Misalignment in Rotor Systems［J］. China Mechanical Engineering， 2016， 27（17）：2379-2383.

［4］ 张西宁， 牛东辉， 李兵. 旋转机械不对中量定量化检测方法［J］. 振动、测试与诊断， 2016， 36（1）：80-85.

ZHANG Xining， NIU Donghui， LI Bing. Study on the Quantitative Detection Method of Misalignment Faults for Rotating Machinery［J］. Journal of Vibration， Measurement amp; Diagnosis， 2016， 36（1）：80-85.

［5］ KIM S M， SUH J H， IM J S， et al. A Smart Memory Type of Data Acquisition System for Shaft Misalignment Maintenance［J］. Journal of Mechanical Science and Technology， 2005， 19（1）：15-27.

［6］ HOTAIT M A， TALBOT D， KAHRAMAN A. An Investigation of the Influence of Shaft Misalignments on Bending Stresses of Helical Gear with Lead Crown［C］∥Proceedings of ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Las Vegas， 2007：929-937.

［7］ 刘慧. 传动轴轴心轨迹测量技术研究［D］. 哈尔滨：哈尔滨工程大学， 2011.

LIU Hui. Research on Measurement Technology of Shaft Axis Trajectory of Transmission Shaft［D］. Harbin：Harbin Engineering University， 2011.

［8］ DEO I S， NATH G. A Non-contact Laser-based Sensor for Surface Analysis of a Rotating Shaft［J］. Laser Physics， 2019， 29（11）：116002.

［9］ 孙小超， 周文， 李明涛， 等. 基于PSD的转轴振动位移测量与分析［J］. 传感器与微系统， 2014， 33（9）：135-137.

SUN Xiaochao， ZHOU Wen， LI Mingtao， et al. Measurement and Analysis of Vibration Displacement of Axis of Rotation Based on PSD［J］. Transducer and Microsystem Technologies， 2014， 33（9）：135-137.

［10］ ZHONG Jianfeng， ZHONG Shuncong， ZHANG Qiukun， et al. Real-time Three-dimensional Vibration Monitoring of Rotating Shafts Using Constant-density Sinusoidal Fringe Pattern as Tri-axial Sensor［J］. Mechanical Systems and Signal Processing， 2019， 115：132-146.

［11］ DODD V R. Shaft-alignment Monitoring Cuts Costs［J］. Oil and Gas Journal， 1972， 9（25）：91-96.

［12］ VERMA A， SARANGI S， KOLEKAR M. Shaft Misalignment Detection Using Stator Current Monitoring［J］. International Journal of Advanced Computer Research， 2013， 3（8）：305-309.

［13］ 黄梅珍. 位置敏感探测器的研究［D］. 杭州：浙江大学， 2001.

HUANG Meizhen. Research on Position Sensitive Detector［D］. Hangzhou：Zhejiang University， 2001.

［14］ 洪波， 尹力， 李毅， 等. 基于激光位移传感器的角焊缝位姿检测［J］. 中国机械工程， 2017， 28（24）：3013-3016.

HONG Bo， YIN Li， LI Yi， et al. Pose Detection of Fillet Welds Based on Laser Displacement Sensor［J］. China Mechanical Engineering， 2017， 28（24）：3013-3016.

［15］ 高玉娥， 刘伟， 吕世猛， 等. 基于位置敏感探测器的六自由度精密位姿测量系统［J］. 光学精密工程， 2018， 26（12）：2930-2939.

GAO Yue， LIU Wei， LYU Shimeng， et al. Six-degree-of-freedom Displacement and Angle Measurement System Based on Two-dimensional Position-sensitive Detector［J］. Optics and Precision Engineering， 2018， 26（12）：2930-2939.

［16］ VULKAN. Applications for Ships and Boats［EB/OL］. https：∥www.vulkan.com/en/downloads.

［17］ 张克猛， 张义忠. 理论力学［M］. 北京：科学出版社， 2008.

ZHANG Kemeng， ZHANG Yizhong. Theoretical Mechanics［M］. Beijing：Science Press， 2008.

［18］ 张军强， 王笑夷， 张新洁， 等. 光锥角对窄带滤光片透射率的影响及补偿方法［J］. 光学学报， 2014， 34（1）：0131001.

ZHANG Junqiang， WANG Xiaoyi， ZHANG Xinjie， et al. Effects and Corrections of Incidence Light Cone on Transmission Characteristics of Narrowband Filter［J］. Acta Optica Sinica， 2014， 34（1）：0131001.

［19］ 李乃成， 梅立泉. 数值分析［M］. 北京：科学出版社， 2011：212-237.

LI Naicheng， MEI Liquan. Numerical Analysis［M］. Beijing：Science Press， 2011：212-237.

［20］ 陈传淼， 胡宏伶， 雷蕾， 等. 非线性方程组的Newton流线法［J］. 计算数学， 2012， 34（3）：235-258.

CHEN Chuanmiao， HU Hongling， LEI Lei， et al. Newton Flow Method for Nonlinear Systems of Equations［J］. Mathematica Numerica Sinica， 2012， 34（3）：235-258.

［21］ 董波. 求解混合三角多项式方程组的同伦方法［D］. 大连：大连理工大学， 2008.

DONG Bo. Homotopy Method for Solving Mixed Trigonometric Polynomial Equations［D］. Dalian：Dalian University of Technology， 2008.

（编辑 陈 勇）