五轴机床旋转轴动态反向误差的球杆仪测量方法研究

摘 要：提出了一种利用球杆仪测量五轴机床旋转轴动态反向误差的新方法，该方法通过一个旋转轴和一个平行于该旋转轴轴线的直线轴进行两轴联动动态测量，测量路径是由球杆仪运动的球面和两联动轴运动的圆柱面相交得到的空间曲线，工作台侧小球设置在圆柱面切线上;通过误差敏感性分析和误差轨迹仿真对比分析，证明了该方法对旋转轴的动态反向误差能够达到充分敏感，并且能够适用于尺寸范围更广的旋转轴;通过在双五轴镜像铣机床上的测量实验，验证了该方法对旋转轴的动态反向误差测量识别的有效性。利用该方法指导旋转轴的伺服调试优化，有利于提高旋转轴的动态反向精度。

关键词：五轴机床;旋转轴;动态误差;球杆仪

中图分类号：TG659    文献标志码：A    文章编号：1671-0797（2022）10-0056-06

DOI：10.19514/j.cnki.cn32-1628/tm.2022.10.015

0    引言

五轴联动机床是目前用于复杂曲面零件高精度加工的主要设备，与三轴机床相比，其加工性能水平很大程度上取决于旋转轴的动态精度。近年来，国内外学者提出了多种五轴机床动态精度检测方法，这些方法按照使用目的可分为两大类：一类是用于五轴机床验收过程中动态性能的综合评价，另一类是用于机床制造或维护过程中的动态精度调试和优化。

针对五轴机床的动态性能综合评价方法，学者们提出了基于球杆仪[1]、R-test[2]、CapBall[3]等多种仪器的测量方法。例如，M. Tsutsumi等人[4]设计了利用球杆仪同时移动一个旋转轴和两个线性轴的圆形轨迹测量方法;B. Bringmann[2]提出了利用R-test直接测量刀尖点在小区域内的3D轨迹来评价动态性能的方法;笔者也提出了一种S轨迹运动学测量方法[5]，通过模拟S试件加工来评估五轴机床的动态精度;L. Andolfatto[3]提出了一种使用CapBall评估五轴机床伺服、几何和动态误差源影响的方法。国际标准ISO/DIS 10791-6： 2014[6]中定义了4种运动测试方法，其中测量圆偏差的AK1和AK2测试用于反映单旋转轴与两直线轴联动的精度，AK3和AK4用于反映五轴联动的动态精度。

上述方法都需要至少3个运动轴联动，测量结果是3个运动轴动态误差的耦合，主要用于综合评价机床的动态性能，不能有效识别单个旋转轴的动态误差源，不适用于五轴机床中单个旋转轴动态性能的调试和优化。

针对五轴机床单个运动轴的诊断调试优化，ISO 230-4： 2005[7]中基于球杆仪或二维光栅盘的圆度测量方法已广泛应用于机床领域，它能够有效、快速地识别运动轴伺服不匹配、动态反向越冲等运动误差，但该方法只能用于直线轴动态精度的调试，仍然缺乏方便有效的方法来测量调试旋转轴的动态精度。旋转轴的动态反向误差往往是曲面加工误差的主要根源，我國提出的最新国际标准S型试件的加工难点也主要存在于旋转轴反向位置的轮廓精度保证上。W. T. Lei[8]和M. Tsutsumi[9]提出了一种旋转轴和直线轴两轴联动球杆仪测试方法，运动模式类似于曲柄滑块机构，通过设置不同的球杆仪位置和长度，可以反映伺服不匹配误差以及反向误差，但该方法对旋转轴的动态反向误差敏感性低，测量范围受限，得到的动态误差轨迹图是不规则、非正交的，误差叠加轨迹复杂多变，工业现场应用较为不便。笔者在文献[10]中也提出了一种单旋转轴和单直线轴的联动运动测量方法，该方法误差轨迹模式具有正交性和规则变化的优点，但对旋转轴动态反向误差的敏感性仍受限，无法达到100%，敏感性随着旋转轴旋转半径的减小而减小。

本文提出了一种新的旋转轴和直线轴两轴联动球杆仪测量方法，该方法能实现对旋转轴动态反向误差100%的敏感性，同时也能分析伺服不匹配、比例不匹配、轴线垂直度等其他误差，其测量效果与直线轴的圆度测量方法相似，可方便、有效地指导旋转轴的诊断和优化。

1    测量路径规划

以AC双摆头结构五轴机床的旋转轴C轴为例，对测量原理进行介绍，如图1所示，球杆仪一侧小球装在主轴侧，球心为Pi，代表刀尖点坐标，另一侧小球装在工作台侧，球心为P0，主轴侧小球随C轴和Z轴联动能够覆盖的运动范围为以C轴轴线为中心线的圆柱面，假设该圆柱面半径为R，另一方面，根据球杆仪的测量原理，主轴侧小球需要在以工作台侧小球中心为球心、以球杆仪长度L为半径的球面Ss上运动，该球面Ss与圆柱面Sc相交的空间曲线即为旋转轴C和直线轴Z两轴联动时能够实现的球杆仪测量轨迹。

为了实现对旋转轴动态反向误差的100%敏感，球杆仪的工作台侧小球P0（x0，y0，z0）按如下方法设置：当刀尖点Pi移动到z0=0位置时，即当旋转轴C轴反向时，P0位于Y轴轴线上，使球杆仪轴线P0Pi与圆柱面Sc相切，如图2所示，故P0坐标为（0，■，0）。

主轴侧小球球心Pi（xi，yi，zi）设置在圆柱面Sc和球面Ss的相交空间曲线上，其坐标满足如下几何关系：

xi=R·sin γ，yi=R·cos γ，zi=Z，xi2+（yi-■）2+zi2=L2          （1）

其中，γ代表旋转轴C轴的旋转坐标角度，Z代表直线轴Z轴的运动坐标位置。

主轴侧小球球心点对应的刀轴方向（TAD）矢量Ti（ii，ji，ki）满足下式：

ii=1·sin γ，ji=1·cos γ，ki=0                  （2）

刀尖点Pi和刀轴方向Ti确定后即可通过后置处理获得测量的NC程序。

笔者在文献[10]中提出了CZ测试方法，该方法使工作台侧小球位于圆柱面上，导致球杆仪的敏感方向无法在旋转轴反向时与刀尖点圆弧相切，因而无法达到对旋转轴反向误差的100%敏感。

2    测量路径分析

2.1    旋转轴反向误差敏感性分析对比

2.1.1    敏感性分析

测试过程中任意一点Pi处，C轴旋转运动的切线方向即为旋转轴动态误差的敏感方向，用uc（cxi，cyi，czi）表示，球杆仪的敏感方向为其轴线方向，用矢量ub（bxi，byi，bzi）表示。

根据uc⊥■可得：

cxi=cos γ，cyi=-sin γ，czi=0          （3）

根据ub=■可得：

bxi=R·sin γ，byi=R·cos γ-■，bzi=Z          （4）

球杆仪对旋转轴动态定位误差的敏感性可以用uc和ub之间的夹角δ表示，该夹角δ角度越小，球杆仪的方向越接近旋转轴的切线方向，意味着球杆仪对旋转轴的反向误差越敏感。

δ=cos-1■=cos-1■     （5）

其中γ的取值范围即为旋转轴C轴测试过程中的旋转行程：

0≤γ≤sin-1■   （6）

从式（5）和式（6）可以看出，当C轴角度为0°时，uc和ub之间的夹角δ为90°，完全不敏感，随着C轴旋转角度从0°增加到最大值，球杆仪对C轴的动态定位误差的敏感性也在增大，到最大旋转角度时，uc和ub之间的夹角δ为0°，即完全敏感，此时正是C轴反向位置，故该方法能够完全反映C轴的动态反向误差。

2.1.2    敏感性对比

旋转轴反向过程受到反向间隙、摩擦力、传动刚度等多种因素影响，旋转轴的动态性能优劣很大程度上反映在其反向过程中动态反向误差的大小。本小节分析对比了本文所提方法与其他方法对旋转轴动态反向误差的敏感性。

从式（5）可以得出本文所提新CZ测试方法中球杆仪对C轴在反向位置的敏感性角度：

δ=cos-1■=cos-11=0°   （7）

文献[10]中得出原CZ测试中球杆仪对C轴在反向位置的敏感性角度：

δCZ=arccos■ （8）

文献[8]中得出CX测试中球杆仪对C轴在反向位置的敏感性角度：

δCX=■-arccos■ （9）

从式（7）（8）（9）的对比可以看出，本文所提方法中，球杆仪对旋转轴反向误差的敏感性为100%，且不受旋转轴旋转尺寸半径R和球杆仪长度L的影响，而文献[8]和[10]中所提方法无法达到100%敏感，且受到R和L的尺寸影响。

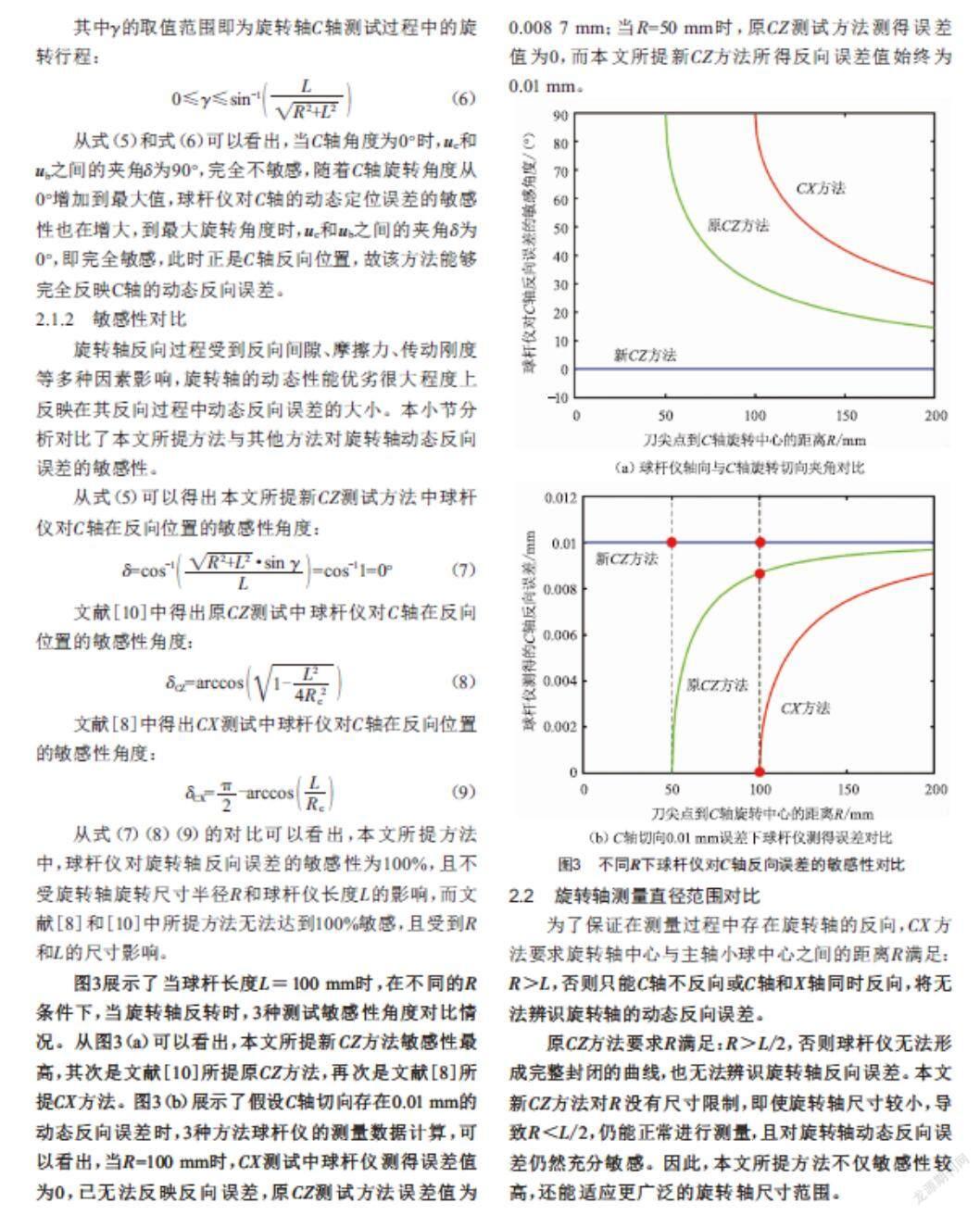
图3展示了当球杆长度L=100 mm时，在不同的R条件下，当旋转轴反转时，3种测试敏感性角度对比情况。从图3（a）可以看出，本文所提新CZ方法敏感性最高，其次是文献[10]所提原CZ方法，再次是文献[8]所提CX方法。图3（b）展示了假设C轴切向存在0.01 mm的动态反向误差时，3种方法球杆仪的测量数据计算，可以看出，当R=100 mm时，CX测试中球杆仪测得误差值为0，已无法反映反向误差，原CZ测试方法误差值为0.008 7 mm;当R=50 mm时，原CZ测试方法测得误差值为0，而本文所提新CZ方法所得反向误差值始终为0.01 mm。

2.2    旋转轴测量直径范围对比

为了保证在测量过程中存在旋转轴的反向，CX方法要求旋转轴中心与主轴小球中心之间的距离R满足：R>L，否则只能C轴不反向或C軸和X轴同时反向，将无法辨识旋转轴的动态反向误差。

原CZ方法要求R满足：R>L/2，否则球杆仪无法形成完整封闭的曲线，也无法辨识旋转轴反向误差。本文新CZ方法对R没有尺寸限制，即使旋转轴尺寸较小，导致R

3    误差轨迹模式仿真

3.1    仿真模型

本节采用图4所示的仿真模型对所提测量方法的误差轨迹模式进行仿真验证，将运动轴的伺服控制系统近似为二阶动态系统[10]，假定R设置为200 mm，球杆仪长度L为100 mm，固有频率ωn=100 Hz，阻尼比ζ=0.7，位置环比例增益为Kp，同时模型中还加入了运动轴的反向间隙误差，细节介绍参见文献[10]。

3.2    误差轨迹模式

本小节对伺服不匹配和反向误差两种常见的动态误差进行仿真验证，首先设定Z轴和C轴具有不同的位置环比例增益Kp值，Kpz设为50 s-1，Kpc设为80 s-1，获得的误差轨迹模式如图5所示。图5（a）为本文新CZ方法结果，图5（b）为原CZ方法结果，图5（c）为CX方法结果，可见本文方法与原CZ方法获得的轨迹均与直线轴圆度测试轨迹近似，均为沿45°或135°的对角线方向变形，而文献[8]的CX测试得到的误差图形形状是不规则的。

其次，设置C轴具有反向间隙误差0.05 mm，引起的误差模式如图6所示。图6（a）为本文新CZ方法结果，图6（b）为原CZ方法结果，图6（c）为CX方法结果，同样的反向间隙值设定，本文新CZ方法得到的C轴反向误差结果为0.05 mm，而原CZ方法仿真结果为0.024 mm，CX方法结果仅为0.015 mm，可见本文提出方法对旋转轴反向误差的敏感性明显优于其他两种方法。

4    实验验证

4.1    实验对象与过程

卧式双五轴镜像铣削技术是实现大型飞机蒙皮绿色高效加工的新技术，AC双摆头动态反向误差的测量优化是控制蒙皮加工壁厚公差的关键因素之一，本小节将所提测量方法应用于上海拓璞12米级大型飞机蒙皮卧式双五轴镜像铣削装备的AC双摆头动态反向误差测量与优化。测量仪器是雷尼绍QC-20球杆仪，安装方式如图7所示，分别进行CZ轴联动和AX轴联动测试。

测试过程中室温波动范围在±2°内，测试前机床预热2 h;主轴侧小球与主轴轴线的同轴误差通过自制的调整工装调整到5 μm范围内，主轴侧小球中心至A轴轴线的距离Laz在Z方向为386.21 mm;主轴侧小球中心到C轴轴线的距离Lcx在X方向为0.23 mm;主轴侧小球中心到A轴轴线的距离Lay在Y轴方向上为0.07 mm;C轴轴线到A轴轴线在Y方向的距离Lca为0.08 mm;球杆仪长度为100 mm;测量速度为1 000 mm/min。参照第2小节方法计算测量路径，并根据文献[10]中方法进行偏置距离换算，获得测量程序。

4.2    实验结果与分析

图8显示了测量获得的AC旋转轴误差轨迹图。红线表示顺时针方向，蓝线表示逆时针方向。图8（a）显示了AX联动的误差轨迹，圆度偏差为0.022 mm，A轴和X轴均存在明显的动态反向误差，A轴反向误差0.014 mm，X轴反向误差0.012 mm，是导致圆度偏差的主要误差源因素。相比之下，图8（b）显示的CZ联动误差较小，圆度偏差为0.017 mm，C轴的反向误差为0.005 mm，Z轴的反向误差为0.008 mm，旋转轴C轴反向性能较好。

为了优化A轴和X轴的反向误差，首先在不引起电机啸叫的情况下，增加A轴和X轴的速度环比例增益，并降低速度环的积分时间常数，然后利用数控系统中的摩擦补偿功能对动态反向误差进行补偿，最后效果如图9所示，可见A轴和X轴的反向误差明显减小，圆度误差控制到0.014 mm。

5    结语

本文提出了一种基于球杆仪空间曲线运动的五轴机床旋转轴与直线轴联动误差测量的新方法，该方法通过一个旋转轴和一个平行于该旋转轴轴线的直线轴联动进行检测，刀具侧小球检测路径是由球杆仪运动的球面和两联动轴运动的圆柱面相交得到的空间曲线，工作台侧小球设置在圆柱面切线上;通过误差敏感性和误差轨迹仿真对比分析可以看出，本文方法对旋转轴的动态反向误差能够达到100%敏感，并且能够适用于尺寸范围更广的旋转轴;在一台双五轴镜像铣机床上进行了实验验证，结果显示该方法能有效识别出旋转轴的动态反向误差，并能够指导调试优化过程;通过对识别出的反向误差进行调试修正，AX轴联动的圆度误差由0.022 mm减小到0.014 mm，A轴动态反向精度显著提高。因此，本文所提出方法能够用于五轴机床调试阶段对旋转轴与直线轴的联动误差进行测量，指导旋转轴伺服参数的优化调整。

[参考文献]

[1] XIANG S T，ALTINTAS Y.Modeling and compensation of volumetric errors for five-axis machine tools[J].International Journal of Machine Tools and Manufacture，2016，101：65-78.

[2] BRINGMANN B，MAGLIE P.A method for direct evaluation of the dynamic 3D path accuracy of NC machine tools[J].CIRP Annals-Manufacturing Technology，2009，58（1）：343-346.

[3] ANDOLFATTO L，LAVERNHE S，MAYER J R R.Evaluation of servo，geometric and dynamic error sources on five-axis high-speed machine tool[J]. Inter-national Journal of Machine Tools and Manufac-ture：Design，research and application，2011，51（10/11）：787-796.

[4] TSUTSUMI M，SAITO A.Identification and compens-ation of systematic deviations particular to 5-axis machining centers[J].International Journal of Machine Tools and Manufacture，2003，43（8）：771-780.

[5] ZHONG L，BI Q Z，HUANG N D，et al.Dynamic accuracy evaluation for five-axis machine tools using S trajectory deviation based on R-test measurement[J].International Journal of Machine Tools and Manufacture，2018，125：20-33.

[6] Test conditions for machining centers-Part 6： Accuracy of speeds and interpolations：ISO/DIS 10791-6：2014[S].

[7] Test code for machine tools-Part 4：Circular tests for numerically controlled machine tools：ISO 230-4：2005[S].

[8] LEI W T，PAUNG I M，YU C C.Total ballbar dynamic tests for five-axis CNC machine tools[J].Inter-national Journal of Machine Tools and Manufac-ture，2009，49（6）：488-499.

[9] TSUTSUMI M，YUMIZA D，UTSUMI K，et al.Evaluation of synchronous motion in five-axis machining centers with a tilting rotary table[J]. Journal of Advanced Mechanical Design Systems and Manufacturing，2007，1（1）：24-35.

[10] ZHONG L，YU J H，BI Q Z，et al.A dynamic two-axis interpolation test with linear and rotary axes in five-axis machine tool[J].The Interna-tional Journal of Advanced Manufacturing Technology，2020，106：91-104.

收稿日期：2022-02-15

作者簡介：钟磊（1986—），男，山东青岛人，硕士研究生，工程师，从事智能制造与数控装备研发工作。