基于B-S模型的沪深300ETF期权实证研究

【摘" 要】论文选取了2022年6月22日到期的沪深300ETF购6月5908A看涨期权和沪深300ETF沽6月4529A看跌期权，利用Python软件构建Black-Scholes模型以计算两只期权在该模型下的理论价值，并与实际收盘价进行对比，检验B-S模型在沪深300ETF期权中的适用性。结果表明：①B-S模型在预测沪深300ETF价格走势方面具有借鉴意义，能够为投资者作出交易决策提供参考;②B-S模型对于看跌期权的定价模拟更加精确。

【关键词】Black-Scholes模型;沪深300ETF期权;期权定价

【中图分类号】F830.9" " " " " " " " " " " " " " " " " " " " " " "【文献标志码】A" " " " " " " " " " " " " " " " " " " " " " " " "【文章编号】1673-1069（2024）07-0051-04

1 引言

随着我国金融市场的不断发展和完善，期权等金融衍生品在投资者资产配置和风险管理中的作用日益凸显。沪深300ETF作为我国金融市场的重要指数之一，其期权合约的推出为我国期权市场注入了新的活力，不仅丰富了投资者的投资选择，也为市场提供了更加多样化的风险管理工具。对于期权而言最核心的内容就是定价，合理的期权定价能为投资者提供对冲、保值的手段，因此，期权的定价问题一直是金融领域的研究热点和难点。目前，国内外学者针对期权定价模型的研究已经取得了丰硕的成果。Black-Scholes模型[1]，简称B-S模型或BS模型，作为经典的期权定价模型，在理论研究和实际应用中均得到了广泛应用。国内外学者对B-S模型的理论性质、假设条件、参数估计等方面进行了深入研究，并提出一些改进的方法[2，3]。同时，也有部分学者尝试引入其他期权定价模型，如CEV模型、HESTON模型、GARCH模型、二叉树模型等与B-S模型进行比较分析[4-6]，但研究结果往往因模型选择、参数设定等因素而存在差异，尚未形成统一的定论。并且目前国内学者研究的对象主要集中在上证50ETF期权[7]上，由于沪深300ETF期权上市时间较短，国内对其研究并不多，基于B-S模型的期权定价实证研究更是寥寥无几[8-10]。因此，本文通过实证研究，探讨B-S模型在沪深300ETF期权定价中的适用性，为投资者提供更加科学、合理的定价依据和风险管理策略，促进金融市场的稳定和发展。

2 理论基础

2.1 沪深300ETF期权

2.1.1 期权

期权是一种合约，是买方向卖方支付一定数量的权利金（即期权费）后拥有的在未来一段时间内（即美式期权）或未来某一特定日期（即欧式期权）以事先商定的价格向卖方购买（即看涨期权）或出售（即看跌期权）一定数量标的物的权利，但不负有必须买进或卖出的义务。

2.1.2 沪深300ETF

沪深300ETF是以沪深300指数为标的的在二级市场进行交易和申购/赎回的交易型开放式指数基金。沪深300指数是由上海和深圳证券交易所最大和最活跃的300家上市公司的股票组成的市值加权指数，是国内基金选择作为业绩基准最多、涉及资产规模最大的指数之一。

2.1.3 沪深300ETF期权

沪深300ETF期权就是期权的买方在支付一定额度的权利金后，获得了在未来某个特定时间，以某个特定价格买入或卖出沪深300ETF指数基金的权利。沪深300ETF期权有两个标的合约：上海证券交易所上市的沪深300ETF期权标的为华泰柏瑞沪深300ETF（代码510300）;深圳证券交易所上市的沪深300ETF期权标的为嘉实沪深300ETF（代码159919）。沪深300ETF期权作为我国金融市场上重要的衍生品工具之一，有助于深沪两市投资者开展套期保值和风险对冲，有利于提高市场定价能力、提升市场流动性和稳定性。

2.2 Black-Scholes模型

Black-Scholes模型，简称B-S模型或BS模型，由Fischer Black和Myron Scholes于1973年提出，该模型认为只有股价的当前值与未来的预测有关，变量过去的历史与演变方式与未来的预测不相关。

2.2.1 Black-Scholes模型的假设条件

①标的资产价格服从对数正态分布;②无卖空机制;③市场无摩擦，即不存在税收和交易成本;④所有证券都是可以无限细分的;⑤金融资产在存续期内无红利及其他所得;⑥不存在无风险套利的机会;⑦无风险利率已知并且不会发生变化，即为常数;⑧该期权是欧式期权，只能在到期日执行，不会被提前执行。

2.2.2 Black-Scholes模型的定价公式

Black-Scholes欧式看涨期权公式为：

C=S0N（d1）-Xe-rTN（d2）

Black-Scholes欧式看跌期权公式为：

P=Xe-rTN（-d2）-S0N（-d1）

其中：

d1=

d2=d1-δ

式中：

C：欧式看涨期权的价格;

P：欧式看跌期权的价格;

S0：标的资产现价;

X：期权行权价格;

r：连续复利的无风险利率;

T：期权到期时间;

N（x）：标准正态分布函数;

δ：标的资产波动率。

通过B-S模型的定价公式可以看出，期权价格的决定非常复杂，合约期限、标的资产现价、无风险利率水平以及标的资产价格波动率等都会影响期权价格。

3 基于B-S模型的沪深300ETF期权实证研究

本文利用Python软件构建Black-Scholes模型对在上海证券交易所上市的两只沪深300ETF期权进行实证检验，将两只期权在该模型下计算的理论价值与实际收盘价进行对比，检验B-S模型在沪深300ETF期权中的适用性。

3.1 数据选取

本文选取了在上海证券交易所上市的华泰柏瑞300ETF购6月5908A看涨期权和300ETF沽6月4529A看跌期权，两只期权均以2022年6月22日为到期日，日期跨度从2021年10月28日到2022年6月22日，共158个交易日。看涨期权的执行价格为5.908元，看跌期权的执行价格为4.529元。

3.2 参数确定

Black-Scholes模型中包含了影响期权价格的5个因素：标的资产价格、期权的执行价格、无风险利率、波动率和期限。

3.2.1 标的资产价格

标的资产价格是期权所关联的基础资产的市场价格，是期权价格变动的基础。当标的资产的价格上涨时，认购期权的价格一般也会上涨，而认沽期权价格则通常是会下降的;反之亦然。因此，在购买期权时需要对标的资产的价格变化有一个准确的预判。本文选取的两个期权均为2022年的沪深300ETF6月期权，作为同期标的资产价格（沪深300ETF）的趋势图如图1所示。

3.2.2 执行价格

执行价格是期权合约规定的标的资产在到期时的交易价格，也称为行权价格。如果是看涨（认购）期权，其行权价是期权买方购买标的资产的价格;如果是看跌（认沽）期权，行权价是期权买方卖出标的资产的价格。行权价格是期权买卖双方事先约定的，其行权价格越高，看涨（认购）期权的价值就越小，而看跌（认沽）期权的价值就越大;反之亦然。

本文所选取的两只期权取自上海证券交易所上市的华泰柏瑞沪深300ETF6月期权，分别是：看涨（认购）期权300ETF购6月5908A，其执行价格为5.908元;看跌（认沽）期权300ETF沽6月4529A，其执行价格为4.529元。

3.2.3 无风险利率

无风险利率是假定在期权持有期内，债券收益率不变，并且投资者可以借入和还款的利率相同。这个参数在计算期权价格时，用于折现期权付款流。无风险利率的变化对期权的价格影响也较大，假如无风险利率上升，则期权购买者的机会成本更高，期权价格也会随之增加。反之，如果无风险利率下降，则期权的价格也会下降。

本文无风险利率用2022年上海银行间同业拆借半年期利率的平均值来代替，代入数据得2.51%。

3.2.4 波动率

波动率在B-S模型中是一个非常重要的参数，它代表标的资产价格波动幅度的大小，波动率越高，期权价格也越高。波动率分为历史波动率和隐含波动率两种，历史波动率是基于过去实际的价格变动情况计算得出的，是一种已知的、可观察的波动率;而隐含波动率是用实际交易中的期权价格反求的估计值，不再具有价格发现和预测的功能。因此，本文采用的波动率是沪深300ETF（510300）在2022年的历史波动率，其计算过程如下：

假设每日的ETF价格=Pi，前一个交易日的价格=Pi-1，从而得出每日的收益率ui=ln，由此可以得出其历史波动率公式为[7]：

δ=

代入数据可得δ=0.227 3。

3.2.5 期限

期权承担着套期保值的功能，期权到期的时间越长，也就意味着套期保值的时间也就越长，而该期权具有的套期保值的价值就越高，同时，该期权的价格也会越高。

本文选取的两只期权均以2022年6月22日为到期日，日期跨度从2021年10月28日到2022年6月22日，共158个交易日。

3.3 实证结果分析

3.3.1 基于B-S模型的沪深300ETF 看涨期权实证结果分析

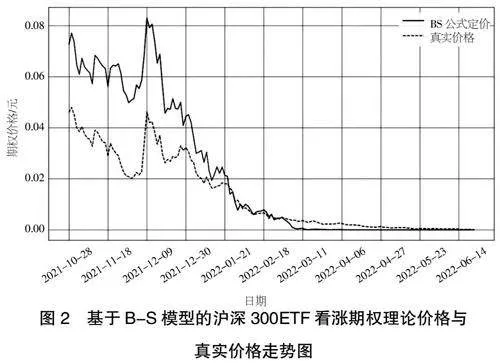
将看涨期权的相关参数代入B-S模型的看涨期权公式中，可以计算出从2021年10月28日到2022年6月22日的看涨期权的理论价格，与实际价格相比较可以得到图2。

从图2可以看出基于B-S模型的沪深300ETF看涨期权理论价格与真实价格变动趋势总体基本一致，但在前期与实际价格差异较大，后期逐渐缩小并趋于一致。这可能是因为距离到期日越远，不确定性越大，市场对标的资产未来的价格走势持悲观态度，因此购买看涨期权的需求较少，导致看涨期权实际价格较低。还有可能是一些交易者同时卖出看涨期权和买入看跌期权，这种交易策略也会导致看涨期权实际价格较低。因此，投资者在购买看涨期权之前，需要对市场情况进行充分的分析和研究。

对于基于B-S模型的沪深300ETF看涨期权理论价格与真实价格的相关性，用协方差进行衡量：①如果协方差大于0，表示二者变化趋势一致，反之变化趋势相反;②协方差的值越大，表示二者的变化程度越相似，越小表示变化程度越不相似。

根据协方差公式：

Cov（x，y）=

可以计算出基于B-S模型的沪深300ETF看涨期权理论价格与真实价格之间的协方差等于0.000 375 414。协方差为正值，表示二者呈正相关，也就是说，基于B-S模型计算的理论看涨期权价格与实际价格变动趋势一致。这说明B-S模型具有一定的可靠性和准确性，可以帮助投资者更好地进行期权交易和风险管理。

3.3.2 基于B-S模型的沪深300ETF看跌期权实证结果分析

和上文一样，可以得到基于B-S模型的沪深300ETF看跌期权理论价格与真实价格走势如图3所示。

从图3可以看出基于B-S模型的沪深300ETF看跌期权理论价格与真实价格变动趋势总体基本一致，在前期与实际价格差异相对较大，但远小于看涨期权的差异程度。

同样，可以计算出基于B-S模型的沪深300ETF看跌期权理论价格与真实价格之间的协方差等于0.031 874 542。协方差为正值，表示二者呈正相关，变动趋势一致。并且与看涨期权相比，看跌期权的理论价格与真实价格的协方差的值更大，说明B-S模型对看跌期权的预测更准确。

4 结论

本文选取了2022年6月22日到期的300ETF购6月5908A看涨期权和300ETF沽6月4529A看跌期权，利用Python软件构建Black-Scholes模型计算两只期权在该模型下的理论价值，并与实际收盘价进行对比发现：①基于B-S模型的沪深300ETF看涨期权和看跌期权理论价格与真实价格变动趋势总体均基本一致，但在前期与实际价格差异较大。这说明B-S模型在预测沪深300ETF价格走势方面具有借鉴意义，能够为投资者作出交易决策提供参考。②与看涨期权相比，看跌期权的理论价格与真实价格的协方差的值更大，说明B-S模型对看跌期权的预测更准确。

B-S模型是期权定价领域的经典模型，其在我国期权市场上也逐渐得到了广泛的认可和应用。然而，随着我国经济的快速发展和市场环境的不断变化，B-S模型在我国期权市场的应用也面临着一些挑战和限制。

首先，由于B-S模型严苛的假设条件在实际交易中几乎无法实现，这也就导致理论价格与真实价格总会存在一定的偏差，因此需要逐步放松限制条件、扩展现有模型才能在一定程度上不断缩小偏差。其次，B-S模型中的5个参数中，期权的执行价格、到期日和无风险利率与实际情况基本相符，标的资产价格是实际交易中可观测的数据，不存在误差，而波动率的取值往往与实际存在较大差异。波动率是根据期权实际价格倒推的一个变动的量，而不是定量，简单地用历史波动率替代会导致理论价格与真实价格存在偏差。最后，我国期权市场发展尚不成熟，存在高波动性、信息不对称、投资者非理性等特征，也会导致B-S模型的应用效果不佳，需要进一步研究和改进。

未来，随着我国期权市场的不断发展和完善，B-S模型的应用将会更加广泛和深入。同时，也可以进一步探索和研究其他期权定价模型，以满足我国期权市场的需求，为我国期权市场的发展作出更大的贡献。

【参考文献】

【1】Black F，Scholes M. The pricing of options and corporate liabilities[J].Journal of Political Economy，1973，81（3）：637-654.

【2】Merton Robert C.Theory of Rational Option Pricing[J].The Bell Journal of Economics and Management Science，1973，4（1）.

【3】Cox J C ， Ross S A ， Rubinstein M .Option pricing： A simplified approach[J].Journal of Financial Economics，1979，7（3）：229-263.

【4】方艳，张元玺，乔明哲.上证50ETF期权定价有效性的研究：基于B-S-M模型和蒙特卡罗模拟[J].运筹与管理，2017（08）：157-166.

【5】姜晓晴.上证50ETF期权定价研究——基于B-S模型与CEV模型[J].吉林工商学院学报，2020（03）：64-70+75.

【6】张翔，李治.沪深300股指期权定价实证研究——基于BS、CEV、Heston模型的对比分析[J].金融，2021，11（04）：319-332.

【7】张昆.基于BS模型的上证50ETF期权实证研究[J].中国商论，2017（25）：169-171.

【8】耿庆峰，叶彬莹.我国沪深300ETF期权定价有效性实证分析[J].金融理论与教学，2023（04）：1-9.

【9】陈乐川，刘文文，何江.基于沪深300ETF的期权定价实证研究[J].中国证券期货，2022（04）：52-59.

【10】封文丽，王艺林.基于单月期限的沪深300ETF期权定价实证研究[J].湖南文理学院学报（自然科学版），2021（01）：9-14.

【基金项目】教育部产学合作协同育人项目：财务共享中心应用实践研究（231100512092343）。

【作者简介】许莉（1990-），女，安徽宿州人，讲师，研究方向：金融学。