基于Optuna超参数优化XGBoost的混凝土抗压强度预测模型

摘 要：为实现对混凝土的抗压强度精确预测以提升工程设计水准和施工质量，基于Optuna超参数优化XGBoost梯度提升算法建立了高效的非线性预测模型。首先，通过从文献中收集的1 110组混凝土试验数据，完成了XGBoost算法与LightGBM、NGBoost、CatBoost等算法的混凝土抗压强度预测精度对比；随后，采用Optuna算法对表现最佳的XGBoost模型进行超参数优化。结果表明，在训练集和测试集中，采用XGBoost算法预测混凝土抗压强度时的精度均高于其他3种算法；经过Optuna超参数优化后，XGBoost模型的预测精度又进一步提升；在测试集中，优化后的XGBoost模型还表现出良好的泛化能力。因此，优化XGBoost模型的混凝土强度预测能力得到证实，可为未来的工程实践提供参考。

关键词：混凝土抗压强度；Optuna；XGBoost；预测模型；模型验证

中图分类号：TU528""" 文献标志码：A

Prediction model for concrete compressive strength based on XGBoost hyperparametric optimization with Optuna

Abstract： This study built a robust nonlinear forecasting model leveraging the XGBoost gradient boosting algorithm， enhanced through hyperparameter optimization via Optuna， to accurately estimate concrete compressive strength， thereby improving engineering design level and construction quality. A comparative analysis was conducted for the predictive accuracy of XGBoost against other algorithms—LightGBM， NGBoost， and CatBoost—utilizing a dataset comprising 1110 unique concrete test samples from existing literature. The evaluation demonstrated that XGBoost outperformed these alternatives in terms of accuracy for both training and testing datasets. Subsequently， Optuna was applied to fine-tune the hyperparameters of the best-performing XGBoost model. The results reveal that the hyperparameter optimization significantly enhances the predictive precision of the XGBoost model. In testing datasets， the optimized XGBoost model demonstrated strong generalization capabilities， confirming its effectiveness in predicting concrete strength and serving as a valuable reference for future engineering practices.

Key words： concrete compressive strength; Optuna; XGBoost; prediction model; model validation

混凝土的抗压强度对结构设计和建筑安全至关重要[1]。精确预测混凝土的抗压强度对提高建筑材料的使用效率和确保结构安全具有重要意义。影响抗压强度的因素众多，如材料配比和养护条件等，传统的经验公式和实验方法由于其局限性难以应对实际工程中复杂多变的情况。例如，基于经验公式的方法通常假设材料成分和环境因素不变，难以适应实际工程中多变的条件，而单纯依靠实验数据的预测方法则存在实验成本高、时间长等问题[2-3]。因此，开发一种科学、高效且精准的混凝土抗压强度预测技术迫在眉睫[4]。

近年来，随着大数据和人工智能技术的发展，基于机器学习的混凝土强度预测展现了全新的研究方向。机器学习通过学习现有数据中的复杂模式，能够有效突破传统方法的局限性，实现对混凝土抗压强度的高精度预测。YEH[5]证明人工神经网络（ANN）在抗压强度预测中的准确性。随后，支持向量机（SVM）[6]、随机森林（RF）[7]和梯度提升树（GBDT）[8]等多种机器学习模型在多个研究中被采用，并展现出更优异的性能。陈洪根等[9]建立了一套基于BP神经网络的粉煤灰混凝土抗压强度预测模型。ABD等[10]提出了一种基于支持向量机的轻质泡沫混凝土抗压强度预测模型，并验证了支持向量机在预测轻质泡沫混凝土抗压强度方面的有效性。此外，学者们还对比了不同核函数下的支持向量机模型，发现采用径向基函数的模型预测精度更高。然而，这些模型的参数调节复杂，通常需要不断优化才能取得最佳效果。

近年来，优化算法在机器学习模型的调参过程中得到了广泛应用。例如，黄炜等[11]利用PSO-BP和GA-BP神经网络模型预测再生砖骨料混凝土强度，显著提高了实验效率。TIEN BUI等[12]比较了鲸鱼优化算法（WOA）、蜻蜓算法（DA）与蚁群优化算法（ACO），发现三者在预测混凝土28 d抗压强度方面均具有高效率，这些算法与ANN相结合，显著提升了预测精度和优化效率。WU等[13]采用GS优化后的SVR（GSSVR）模型对混凝土抗压强度进行了预测，发现GSSVR模型明显优于原SVR模型。超参数选择与优化仍是实际应用中的一大挑战，尤其是在处理高维数据时，模型易面临过拟合或欠拟合的问题。因此，如何利用高效的优化算法提高模型的搜索效率和精度，成为目前的研究重点。

本研究针对上述问题，基于Optuna-XGBoost模型建立了混凝土的抗压强度与影响因素之间的非线性映射关系，优化模型参数以实现对混凝土抗压强度的精准预测，并通过实验数据对模型性能进行了验证和评估。

1 数据集

1.1 数据分析

本研究所采用的数据集来源于文献[5，14]中提供的共计1 110组混凝土抗压强度试验数据。以影响混凝土抗压强度的8个参数（水泥、矿渣、粉煤灰、水、减水剂、粗骨料、细骨料、龄期）为输入数据，抗压强度的预测值为输出数据。数据集描述性统计信息见表1。

对输入数据和输出数据进行相关性分析，得到各变量间热力相关图如图1所示。变量间的相关性与图中colorbar颜色相关。

由图1可知，水泥与抗压强度的相关性系数达到了0.49，证明两变量间存在一定程度的正相关性，水和细骨料的相关性系数达到-0.42，表明变量之间存在一定程度的负相关性。整体来看，各变量之间的相关性系数较低，说明变量之间不存在明显的特征重叠。该数据集可以有效地避免模型因过度依赖某一特征而导致预测性能下降的风险。

1.2 数据预处理

将1 110条数据采用8∶2原则随机分割，即训练集为888条，用于训练预测模型；测试集为222条，用来评估预测模型。对训练集采用5折交叉验证，可以有效减少因数据随机性划分带来的评估误差和过拟合情况。

为了让特征变量在相同的尺度下，避免因特征值范围不同而导致模型训练时的偏差，采用Python语言中sklearn.preprocessing软件包的StandardScaler函数对特征变量和目标变量进行标准化处理，使其均值为0，标准差为1。其计算公式为

式中：x'为标准化后的值；x为当前值；μ为样本均值；σ为样本标准差。

2 模型建立

2.1 XGBoost原理

CHEN等[15]基于回归树的提升算法提出XGBoost（极限提升树）。它通过逐步构建新的模型来纠正前一个模型的残差。每一轮中，新模型是对损失函数的负梯度的拟合。其主要优势在于在目标函数中引入正则化，以管理模型复杂度，避免过度拟合。此外，通过二阶泰勒展开简化目标函数，进一步考虑梯度的变化趋势，可以实现更快速、更准确的拟合。

XGBoost模型由多个CART决策树组成，每棵树都有自己的结构和树叶节点的权重，输出为多个树的和，其简化的训练流程如图2所示。

假设研究中训练采用的数据集样本为xi，yi，其中，xi∈Rm，yi∈R，则XGBoost模型表达式为

CART决策树的空间F表达式为

F=fx=ωqxq：Rm→T，ω∈RT（3）

式中：q：Rm→T代表决策树将样本数据映射到树叶子节点的函数；T为树叶子节点数量；ωi为树叶子节点i上的得分。

XGBoost的基本思路是依赖于前一步优化的结果训练后一步。即每次迭代都是在上一次迭代基础上增加一个子模型fxi，从而不断地使预测值接近实际值。通过s次迭代使目标函数达到最小值，即目标函数也可表示为

2.2 k折交叉验证

为避免按8∶2随机划分数据集导致数据利用率低，减少数据集划分的偏差和方差，本研究采用k折交叉验证（k=5）将每一部分数据都用于训练与测试，这可以充分利用数据，且能够有效地避免过拟合并确保模型的泛化能力。其主要原理如下：

在五折交叉验证中，原始数据集被平均分成5个互不重叠的子集。在每一次迭代中，选择其中一个子集作为验证集，剩余4个子集作为训练集。通过这种方式，模型将被训练和验证5次，每次使用不同的子集作为验证集。最后，将这5次验证的结果求取平均，从而获得一个更为可靠和精准的模型性能评估指标。

2.3 Optuna超参数优化

Optuna是一种基于改进的贝叶斯优化方法，具备自动优化超参数以减少拟合误差的能力。它能够动态构建参数搜索空间，并高效地执行修剪和搜索操作。Optuna会根据已有的历史运行数据来选择下一个超参数组合的各个取值，并基于此信息选定一些潜在的超参数组合区域，在这些区域内进行进一步的搜索以获得更优解。随着新的结果不断生成，Optuna持续更新搜索区域并评估其效果，从而逐步优化超参数组合的准确性与可靠性。

3 实验结果与分析

3.1 评估指标

本研究采用量化的决定系数（R2）、平均绝对误差（MAE）和均方根误差（RMSE）来评估预测模型的准确性。其公式如下：

R2表示实际值的总变异中能够通过模型解释的比例，其值介于0和1之间。R2越接近1，表示模型对数据的拟合程度越高。MAE是实际值与预测值之间绝对差值的平均值，能够直接反映出预测值与实际值的偏离程度。MAE越小，表示模型预测效果越好；RMSE是均方根误差，具有与原数据相同的量纲，使其更易于解释。RMSE越小，表示模型的预测效果越好。

3.2 性能比较

为验证XGBoost梯度提升算法的准确性，本研究将基于CatBoost、LightGBM、NGBoost模型读取划分的训练集和测试集，分别训练和测试，并与XGBoost进行预测性能对比，4种模型均采用相同的数据预处理方式及五折交叉验证的方式确保模型泛化能力。

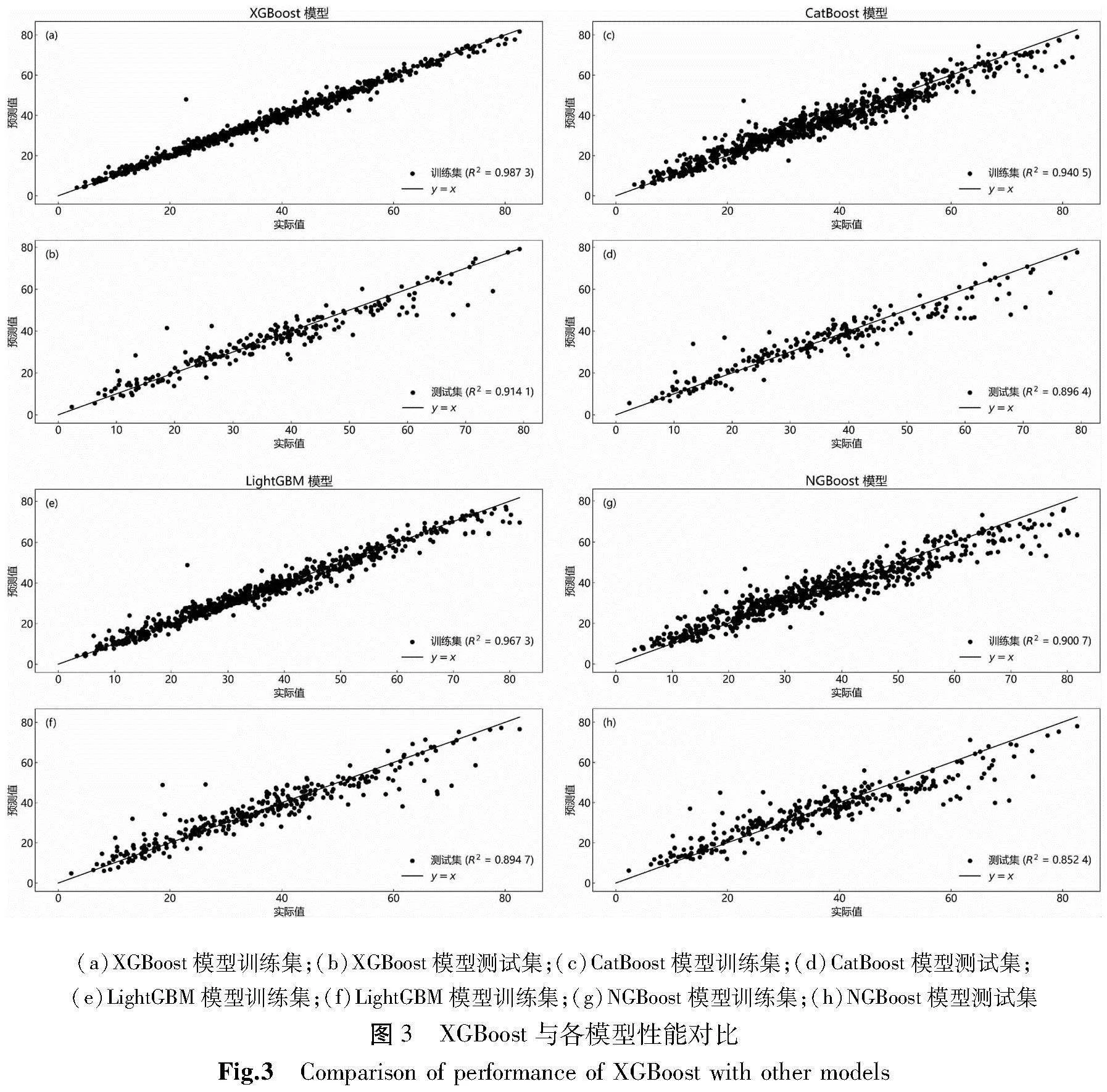
从图3可以看出，CatBoost模型在训练集上的拟合效果一般，R2达到0.940 5，点分布较为集中，其预测值和实际值吻合良好，表明模型在训练数据上的预测能力较强。然而，在测试集上，R2为0.896 4，略有下降，说明模型的泛化能力较差。LightGBM模型在训练集上的拟合效果较好，R2值为0.967 3，其预测值和实际值吻合较好，表明模型能够很好地捕捉训练数据中的特征。然而，测试集上的R2值仅为0.894 7，与训练集相比差异较大，表明模型对新数据的泛化能力有待提升。NGBoost模型在训练集和测试集上的拟合效果均相对较差，R2值明显低于其他模型，说明该模型整体预测精度不如其他模型。XGBoost模型在训练集上的拟合效果最好，R2值达到0.987 3，其预测值和实际值吻合最好，拟合训练数据优度最高。同时，在测试集上的R2值也达到了0.914 1，表明XGBoost模型在训练集和测试集上的表现均优于其他模型，具有较高的预测精度和较好的泛化能力。

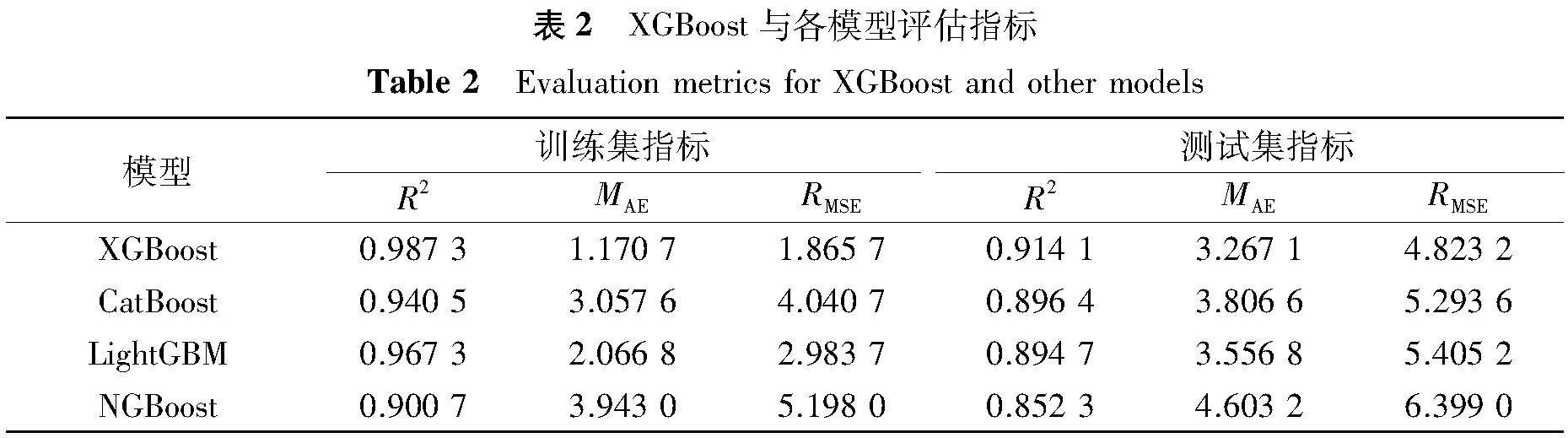
将各模型预测数据与实际数据分别代入式（6）和式（7）中计算评估指标，得出4种模型的预测精度由高到低分别如下：

1）XGBoost模型的MAE和RMSE在训练集上分别为1.170 7和1.865 7，在测试集上分别为3.267 1和4.823 2，均低于其他3种模型。这表明XGBoost模型在混凝土抗压强度预测中具有最高的准确性和稳定性，泛化能力最强。

2）LightGBM模型训练集上的MAE和RMSE分别为2.066 8和2.983 7，测试集上的MAE和RMSE分别为3.556 8和5.405 2，表明模型在测试集上的误差相对较大，尤其是RMSE较高，说明模型在处理一些极端数据点时存在不足。

（a）XGBoost模型训练集；（b）XGBoost模型测试集；（c）CatBoost模型训练集；（d）CatBoost模型测试集;（e）LightGBM模型训练集；（f）LightGBM模型训练集；（g）NGBoost模型训练集；（h）NGBoost模型测试集

3）CatBoost模型训练集上的MAE和RMSE分别为3.057 6和4.040 7，测试集上的MAE和RMSE则为3.806 6和5.293 6，说明模型在测试集上的误差较训练集较大，模型的泛化能力有待提高。

4）NGBoost模型训练集上的MAE和RMSE分别为3.943 0和5.198 0，测试集上的MAE和RMSE分别为4.603 2和6.399 0，显示出NGBoost模型在训练集和测试集上的误差均较大，预测性能和泛化能力较弱。

3.3 Optuna超参优化后的性能比较

为了进一步提高XGBoost模型在混凝土抗压强度预测中的表现，本研究利用Optuna来优化XGBoost模型关键超参数。超参数调节开始之前，需要将调节的超参数的范围值列出，多个不同超参数的不同取值之间排列组合，最终将组成一个参数空间。具体优化的参数及范围如表3所示。

基于表3中的搜索范围，利用Optuna超参数优化算法得到的最优参数结果如表4所示。

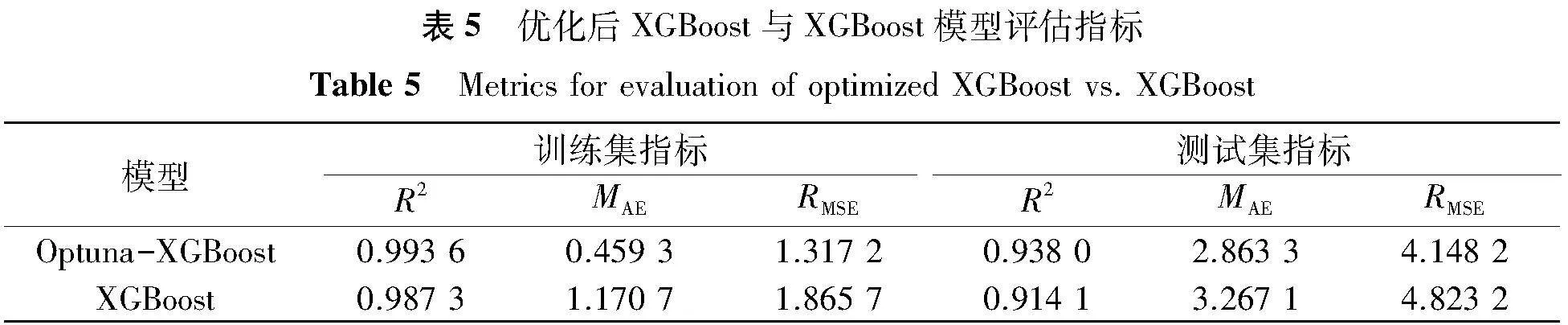
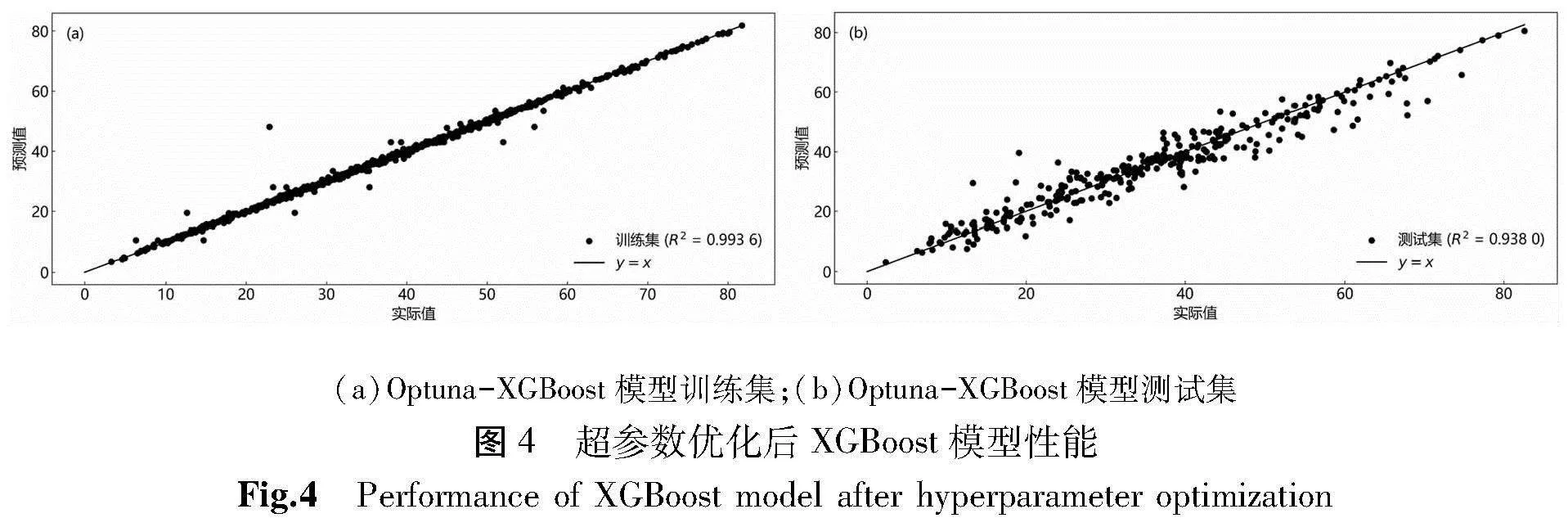
将优化后的主要参数代入XGBoost模型中，与优化前模型性能进行对比。从图4可以看出，基于Optuna优化后的XGBoost模型拟合效果更优。在训练集上优化后XGBoost的R2提高了0.006 3，点分布高度集中，预测结果准确。在测试集上优化后XGBoost的R2提高了0.023 9，表明优化后模型泛化能力也有了较大的提升。将两种模型训练数据与测试数据分别代入式（6）和式（7）中计算评估指标，结果如表5所示。

从表5可以看出，基于Optuna算法优化后的XGBoost模型在训练集上的MAE降低了约60.8%，RMSE降低了约29.4%；在测试集上MAE降低了约12.4%，RMSE降低了约14.0%。结果表明，经Optuna优化后的XGBoost在训练集和测试集的预测能力和泛化能力有了较大的提升。

3.4 模型验证

为进一步验证上述建立的Optuna-XGBoost模型泛化能力，本研究将自有数据集的自变量输入训练好的Optuna-XGBoost预测模型中评估其性能。表6为自有数据集描述性统计信息。

由表1和表6可以看出，该数据集与文献［5］提供的数据集具有一定的差异性，能够有效地验证模型的泛化能力。

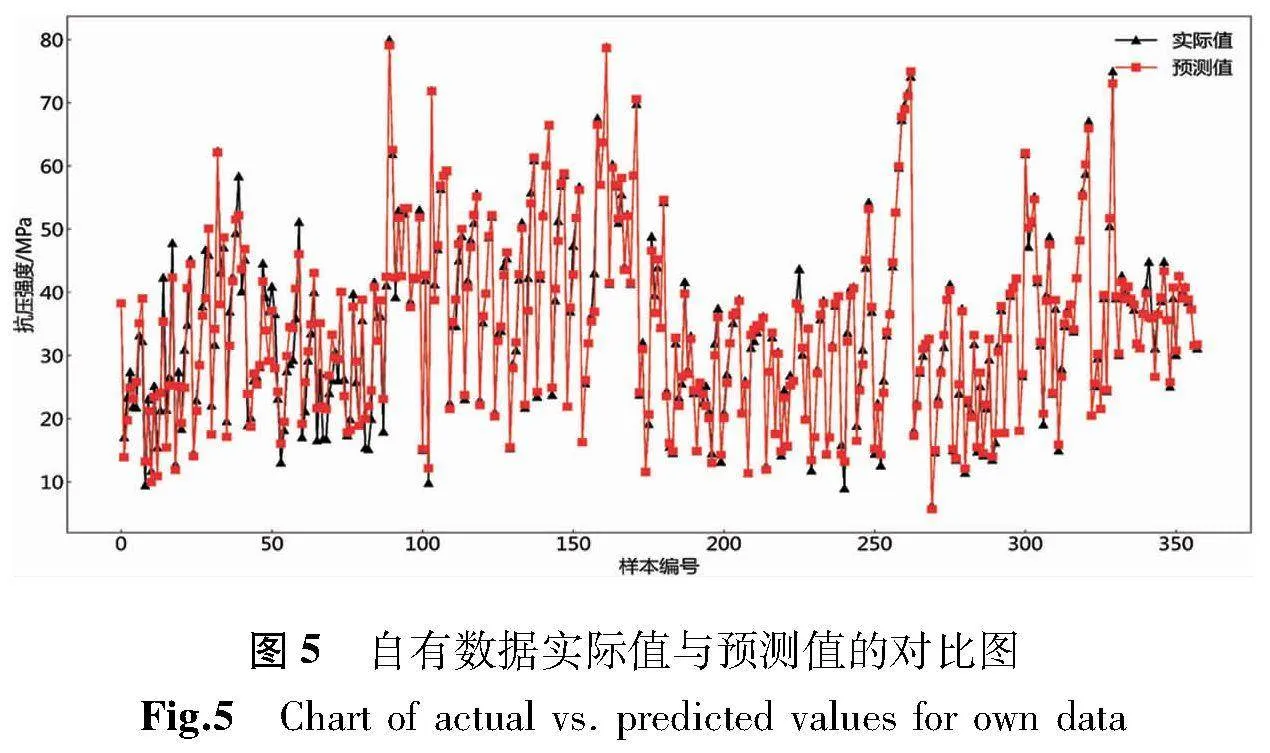
由图5可以看出，Optuna-XGBoost模型在测试集上的预测值与实际值的拟合度较高。具体来说，该模型在各项评估指标上表现出色，其R2达到0.975 1，MAE为1.466 7，RMSE为2.273 9。本文所构建的基于Optuna-XGBoost的混凝土抗压强度预测模型具备较强的泛化能力和应用价值。

4 结论

1）基于文献中的1 110组混凝土试验数据，XGBoost模型在混凝土抗压强度预测准确性方面优于LightGBM、NGBoost和CatBoost模型。

2）经Optuna超参数优化后，XGBoost模型的混凝土抗压强度预测能力又进一步提升。

3）基于自有数据的验证表明，Optuna-XGBoost模型具有良好的泛化能力。

参考文献：

[1]李九阳， 朱岳鹏， 范辛美， 等. 智能混凝土裂缝自监测性能试验研究[J]. 邵阳学院学报（自然科学版）， 2024， 21（2）： 73-81.

[2]HENIGAL A， ELBELTGAI E， ELDWINY M， et al. Artificial neural network model for forecasting concrete compressive strength and slump in Egypt[J]. Journal of Al-Azhar University Engineering Sector， 2016， 11（39）： 435-446.

[3]DEBBARMA S， RANSINCHUNG R N G D. Using artificial neural networks to predict the 28-day compressive strength of roller-compacted concrete pavements containing RAP aggregates[J]. Road Materials and Pavement Design， 2020， 23（1）： 149-167.

[4]李姣阳. 基于Stacking集成算法的混凝土28 d抗压强度预测[J]. 广东建材， 2024， 40（6）： 19-23.

[5]YEH I C. Modeling of strength of high-performance concrete using artificial neural networks[J]. Cement and Concrete Research， 1998， 28（12）： 1797-1808.

[6]SOBHANI J， KHANZADI M， MOVAHEDIAN A. Support vector machine for prediction of the compressive strength of no-slump concrete[J]. Computers and Concrete， 2013， 11（4）： 337-350.

[7]吴贤国， 刘鹏程， 陈虹宇， 等. 基于随机森林的高性能混凝土抗压强度预测[J]. 混凝土， 2022（1）： 17-24.

[8]ABDULALIM ALABDULLAH A， IQBAL M， ZAHID M， et al. Prediction of rapid chloride penetration resistance of metakaolin based high strength concrete using light GBM and XGBoost models by incorporating SHAP analysis[J]. Construction and Building Materials， 2022， 345： 128296.

[9]陈洪根， 龙蔚莹， 李昕， 等. 基于BP神经网络的粉煤灰混凝土抗压强度预测研究[J]. 建筑结构， 2021， 51（增刊2）： 1041-1045.

[10]ABD A M， ABD S M. Modelling the strength of lightweight foamed concrete using support vector machine （SVM）[J]. Case Studies in Construction Materials， 2017， 6： 8-15.

[11]黄炜， 周烺， 葛培， 等. 基于PSO-BP和GA-BP神经网络再生砖骨料混凝土强度模型的对比研究[J]. 材料导报， 2021， 35（15）： 15026-15030.

[12]TIEN BUI D， ABDULLAHI M M， GHAREH S， et al. Fine-tuning of neural computing using whale optimization algorithm for predicting compressive strength of concrete[J]. Engineering with Computers， 2021， 37（1）： 701-712.

[13]WU Y Q， ZHOU Y S. Hybrid machine learning model and shapley additive explanations for compressive strength of sustainable concrete[J]. Construction and Building Materials， 2022， 330： 127298.

[14]SIDDIQUE R， AGGARWAL P， AGGARWAL Y. Prediction of compressive strength of self-compacting concrete containing bottom ash using artificial neural networks[J]. Advances in Engineering Software， 2011， 42（10）： 780-786.

[15]CHEN T Q， GUESTRIN C. XGBoost： a scalable tree boosting system[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco California USA. ACM， 2016： 785-794.