重视数学活动体验 发展逻辑推理素养

［摘 要］ 逻辑推理是数学核心素养的要素之一，重视数学活动体验，发展逻辑推理素养非常重要. 在实施实际教学时，教师一定要放眼看大局，引导学生通过观察、验证等具体过程，让学生掌握逻辑推理的基本方法，有效推进数学教育的良性循环.

［关键词］ 逻辑推理；数学活动；逻辑推理能力

逻辑推理是一种能力，也是一种素养. 若学生具备良好的逻辑推理能力，则学生在解题时可以快速地将已知和未知建立联系，形成有效的解题策略，以此提升解题效能. 另外，培养学生逻辑推理能力对发展学生的数学思维能力、提升学生的创新意识等具有十分重要的作用，因此培养学生逻辑推理能力势在必行. 不过学生逻辑推理能力不是一朝一夕就能养成的，也不是单凭教师教授能完成的，这是一个非常缓慢的过程，要在日常教学中不断去锻炼. 笔者对于如何培养学生的逻辑能力，提出了若干意见供参考，若有不足，请指正！

鼓励数学猜想，有效开发逻辑

思维

数学猜想实际上是一种数学想象，它是培养学生创新意识，发展学生逻辑推理能力的必经之路. 在数学教学中，教师要提供丰富的想象素材，鼓励学生大胆猜想，并提供机会让学生思考、交流、归纳，以此有效开发学生的逻辑思维.

例如，在教学“多边形的外角和”时，教师引导学生类比多边形的内角和公式的推导过程，鼓励学生自由大胆地猜想与验证，发挥想象能力，培养学生敢想、敢探索的好习惯，促进学生类比和归纳等推理能力的提升. 教学设计如下：

1. 回顾旧知，自动类比

问题1：你还记得多边形内角和公式及其推导过程吗？

问题2：你能画出任意的三角形的外角吗？

问题3：在练习本上画一个任意的五边形，作出它的外角.

问题4：结合以上作图经验，请谈一谈你对外角的理解.

设计意图 引导学生回顾旧知，不仅可以巩固旧知，还可以让学生自然地与新知建立联系，引发类比，以此为新知的探索做铺垫. 在探索多边形的外角和时，以三角形为基础，让学生通过操作认识和理解多边形的外角，以此让抽象的概念更为直观化、形象化，更易于学生理解和接受. 在此基础上，教师鼓励学生将三角形外角的探究经验迁移至五边形，通过动手做、用嘴说，进一步强化学生对多边形的外角的理解，培养学生的逻辑表达能力.

2. 充分想象，猜想结论

问题5：结合以上探究经验，你认为多边形的外角和是多少呢？

在此过程中，教师不要急于启发和指导，应放手让学生自己去猜想，并找到适合自己的推理方式. 从学生探究反馈来看，学生会借助特殊三角形、四边形、五边形的外角和形成猜想，然后借助推理多边形内角和的经验进行验证.

设计意图 在教学中，教师为学生搭建了一个自由猜想与验证的平台，有效地激活了学生的思维，提升了学生探索的积极性. 在教学中，教师预留时间呈现学生思考过程：有的学生提出多边形的外角和是360°，并通过测量验证了自己的结论；有的学生得到了一样的结论，但采用的方法不同，应用拼接法验证了自己的猜想；还有的学生通过“算”验证了结论，如五边形有5个平角，其和为900°，它的内角和为540°，则外角和为360°. 这样教师将探究的主动权交给学生，使学生的想象力得到了充分发挥. 另外，学生利用不同方法进行验证，既丰富了学生的认知，积累了丰富的活动经验，又锻炼了学生的逻辑推理能力.

放手让学生体验，积累数学活

动经验

在传统教学中，大多数公式、定理、结论的证明都是以教师演绎为主，很少提供机会让学生猜想、推理、验证. 大多数教师认为，对于这些既定事实，重点是记住、会用. 要知道，这些公式、定理、结论的证明蕴含着丰富的思想方法，是培养学生逻辑推理的重要工具，因此在实际教学中，教师要提供时间和机会让学生去发现、去体验、去探索，学生在实践的过程中，可以积累丰富的经验，稳定提升逻辑思维能力.

例如，在教学“完全平方公式”时，教师基于最近发展区创设问题情境，巧妙地设计图形诱发猜想，并鼓励学生运用数形结合思想方法进行验证，以此通过观察、猜想、验证等活动，培养学生逻辑推理能力. 教学设计如下：

1. 创设问题情境，激发学生的探究欲

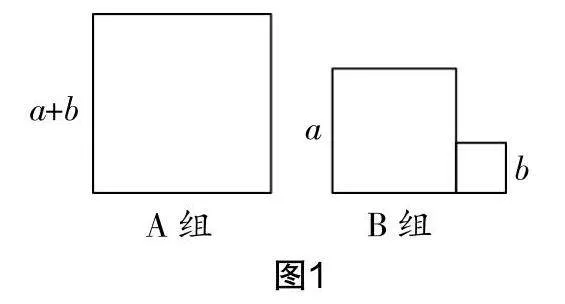
问题情境：为了打造一个美丽的环境，需要让学生养成自觉讲究卫生的习惯，学校每周五会举行一次大扫除. 大扫除时，教师安排A，B两组学生共同打扫食堂地面区域. 为了公平，教师首先安排两组分别完成一块边长为a的正方形区域的打扫. 打扫后发现有些区域没有打扫干净，于是教师要求两组扩大打扫范围，A组打扫的区域每条边长增加长度b，B组增加一块边长为b的正方形区域. 如此安排是否依然能够确保公平呢？

设计意图 从学生熟悉的生活情境出发，将生活与数学建立联系，激发学生的探究欲. 同时，对是否公平的探索，有效地吸引住了学生的注意力，通过实际问题的解决为公式的推导奠定基础.

2. 巧借图形，诱发数学猜想

教师先让学生说一说自己的猜想，然后启发学生将以上问题情境用图形的方式表达出来，由此借助图形进一步引导学生观察、猜想、推理. 教师放手让学生动手画，并展示学生的画图结果，如图1所示.

学生认真观察图1，认为这样的安排有悖公平，A组打扫的区域大于B组. 此时，教师指出：直接观察并不能得到最终的结论，能否通过其他方法验证你们的猜想呢？在教师的启发下，学生积极互动，从数的角度进行了分析：学生给出A组打扫的区域面积为（a+b）2，B组打扫的区域面积为a2+b2，至此问题转化为了比较（a+b）2与a2+b2的大小. 学生通过观察和计算，判定（a+b）2≠a2+b2且（a+b）2>a2+b2.

设计意图 引导学生利用图形和计算对自己的猜想进行思考与验证，发展学生的直观想象和逻辑推理素养，加强学生对完全平方公式的印象.

3. 巧借数形结合，引导数学论证

通过以上两个环节的探究，学生利用图形和计算验证了猜想，为了让学生体会数学的严谨性，教师让学生又思考了一个问题：（a+b）2比a2+b2大多少？

问题给出后，教师鼓励学生在原有图形的基础上画一画，看看自己有何发现. 教师预留充足的时间让学生分一分、议一议，学生得到了新的图形（如图2所示）.

这样借助图形对比不难发现，A组增加的区域面积为b2+2ab；B组增加的区域面积为b2，显然A组增加的区域面积更多，且多2ab. 在此基础上，学生得到了结论：（a+b）（a+b）=a2+2ab+b2，即（a+b）2=a2+2ab+b2.

设计意图 引导学生从数和形等多角度进行分析，让学生经历完全平方公式的推导过程，加深学生对完全平方公式的理解，有效提升学生的逻辑推理能力.

教授逻辑推理方法，提高逻辑

推理能力

周知，正确的方法是走向成功的金钥匙，因此学生逻辑思维能力的培养离不开正确的方法，这应该得到教师的重视. 逻辑推理的基本方法一般有综合法、分析法、反证法等，教师要重视引导学生关注不同方法的区别与联系，以此加深学生对不同方法的理解，以便学生解题时能够进行合理的选择，切实提高解题效率.

例如，在学习“图形的旋转与折叠”后，教师设计了这样一个问题：如图3所示，已知△ABC是等腰三角形，其中AB=AC. 在BC边上任意取一点D，连接AD，得到△ADC. 现将△ADC沿AD边翻转，得到四边形ABDC′. 问四边形ABDC′是否为平行四边形？

对于大部分初中生来讲，他们的空间想象能力较差，因此他们遇到翻折或旋转问题时往往会显得束手无策. 教师先是引导学生对题目的特点进行深度剖析，确定该题用反证法更有效. 假设四边形ABDC′是平行四边形，则BD=AC′，又根据翻折定理可得DC=AC′，即DB=DC，则D为BC边的中点，显然与已知不符合，所以该假设不成立，即四边形ABDC′不是平行四边形.

有些问题从正向论证可能无从入手，此时不妨从反向出发，通过逆向推理，可以让解题过程变得更加简洁明了. 掌握逻辑推理的基本方法，可使论证过程更加清晰，学生的学习信心更强，学生的数学核心素养得到发展.

总之，在数学教学中，教师应给学生发现、提出、分析和解决问题提供充足的时间和空间，并在学生观察、猜想、验证等过程中，充分、有效地开发学生的逻辑思维能力，加强学生的数学学习能力，提升课堂教学效率.