基于“提问能力”培养的数学教学策略研究

［摘 要］ 布鲁巴克提出：让学生自主提出问题是最精湛的教学艺术. 完整的数学教学包括学“问”与学“答”，数学教育应将培养学生的问题意识作为重要的教学目标，让课堂成为问题发现与问题解决互相促进的场所. 基于“提问能力”培养的数学教学策略可从以下几方面着手：创设问题发现情境，激发提问意愿；确定学生主体地位，明确提问方式；开放教学时空界限，拓宽提问途径.

［关键词］ 提问；情境；问题

爱因斯坦认为，提出一个问题往往比解决一个问题更重要，解决一个问题或许仅需一个实验或知识点即可，而提出一个问题，则需一定的想象力与创造力. 《义务教育数学课程教学标准（2022年版）》（下称“课标”）明确提出：要培养学生的问题意识，要让学生在数学教学中获得良好的提问能力［1］. 然而，虽然中国历来讲究做“学问”，但学生更多的是做“学答”，这种训练模式使得很大一部分学生提问意识薄弱，即使在存疑的情况下，也不敢提问、不愿提问或不会提问.

基于此，笔者结合自身多年的执教经验对此进行了大量的研究与思考，认为可从以下几个方面来培养学生的提问能力.

创设问题发现情境，激发提问

意愿

创新意识的形成往往源自问题，而问题的形成又源于情境，离开情境作为依托的问题，就如同种子失去了土壤. 问题情境分为问题发现情境与问题解决情境两类，其中问题发现情境从本质上来讲就是一种利于问题产生的背景材料，学生在这种背景下容易形成自主提问的心理倾向，产生提问意愿.

问题发现情境是激发学生产生提问意愿的重要载体，一般且具备如下特征：①民主性. 此类问题首先应具备民主、和谐、自由的氛围，让学生感知思维自由，产生心理安全感. ②适中性. 问题发现情境必须落于学生认知范围内或处于学生的“最近发展区”，与学生的学习、生活或社会经验有一定联系，且符合学生的心理特征，能给学生带来积极的情感体验. ③挑战性. 问题发现情境的呈现并不是为了传递问题本身，而是为了给学生提供充足的探索空间，是问题形成的“助产师”. ④开放性. 问题发现情境从形式上来看，也是问题的一种，只是这类问题更具初始性、方向性或模糊性特征，需要给学生提供多样化、开放性的提问方式，不能将学生的思维禁锢在特定的框架内.

基于对问题发现情境特征的分析，教师应充分了解学生的“最近发展区”，联系学生的生活经验从多维度收集情境素材，借助一些学生感兴趣的社会热门话题、先进技术或科学等素材创设问题情境，以引发学生产生认知冲突，形成疑惑与求知欲［2］.

案例1 “中位数与众数”的教学

对初中生而言，中位数与众数的概念过于抽象，容易出现概念混淆或模糊不清等现象. 为了让学生对这部分知识产生探究欲，并形成自主提问的意愿，笔者结合校运动会，创设了如下问题情境：

用PPT展示运动会上初三男子撑竿跳比赛参赛情况与具体成绩：共有9名学生参赛，预赛时平均高度为4.1 m，原定取成绩的前6名晋级决赛，而031号李刚所跳的高度为4.2 m，那么他能否晋级呢？

要求学生对照表1所展示的具体成绩，进行分组讨论，并自主提出你想探索的问题.

刚刚过去的运动会是学生津津乐道的生活事件，教师以此作为问题情境，不仅成功地激发了学生的探索热情，还让学生对本节课的教学充满了向往.

学生经讨论后，自主提出以下问题：①初三男子跳高的平均成绩是怎么计算而来的？②平均数是否能反映初三男子撑竿跳的平均水平？③如果去掉一个最高分，再去掉一个最低分之后统计预赛成绩的平均数，是不是更合理一些？④预赛成绩出现了0这个极端数据，在这种情况下该用什么方法来表示这组数据的集中度呢？

每一个问题都体现出学生的思维，沿着学生的思维进行授课，教学效率明显得到提高.

这是一个简洁明了的问题情境，以学生感兴趣的运动会作为情境素材，因贴近学生的生活，更容易激发学生提问的心理倾向. 本节课是在学完平均数之后的授学，因此学生首先就想到与“平均水平”相关的问题，不仅起到巩固旧知的作用，还成功地引发了自身对新知的思考与探索. 因此，这是一个成功的问题提出情境，符合学生认知发展的需求，对培养学生的提问能力具有显著的作用.

确定学生主体地位，明确提问

方式

课标一再强调学生才是课堂的主人，学生在课堂中自始至终都应处于主体地位. 实践证明，成功的教育向来不是教师直接告知学生知识与答案，而是引导学生获得自主发现、分析并解决问题的能力. 如概念或定义等的抽象过程，常存在生动的思维历程，这些生动活泼的思维是学生规范提问意识、形成探索能力的重要契机.

课堂教学活动的开展，以学生主体参与知识建构为主，这个建构过程是师生积极互动，促进学生思维探索的过程. 因此，不论是新知教学，还是复习教学，抑或是实践活动开展，都应在“以生为本”的基础上因材施教，让每个学生都能明确提问方式，提出高质量的问题.

案例2 “三线八角”的解题教学

笔者准备了几道经典例题，带领学生从“A”字形与“Z”字形等直观图形中感知解题技巧，并通过变式帮助学生建立处理此类问题的能力，让学生明确同位角、同旁内角、内错角的本质. 课堂进展顺利，与预设没有太大偏差. 本以为这是一节无可挑剔的成功课堂，没想到学生的课后作业却错误百出.

为了探寻问题出在哪儿，笔者课后与学生进行了交流，不少学生提出：有没有更简单的方法来解决这一类问题呢？

虽然这是一个模糊的想法，对于知识点而言没有明确的指向性，却道出了学生内心最真实的想法与愿望. 为了帮助学生解开这个谜团，笔者要求学生带着此问查阅资料并细细揣摩教材所应用的规范表达方式，争取从中获得一些新的发现.

果不其然，学生经自主探索后提出了一个高质量的问题：三线八角类的问题都是从平行判定定理类的问题拓展而来的，其中“两直线被第三条直线所截”是反复出现的一句话，为什么将两条线称为被截线，而将第三条线称为截线呢？

此问的提出，也让笔者意识到上节课失败的根源就在于学生对什么是截线，什么是被截线并不了解，在这种状态下做题，必然漏洞百出.

经过合作交流，学生获得如下认识：平行线判定定理都蕴含在这三条直线的关系里，只有明确谁是被截线，谁是截线才能厘清其中的关系，至于各种角的命名则由其位置关系所决定，为判定两条被截线的位置关系服务.

为了充分凸显学生在课堂中的主体地位，并规范学生的提问方式，师生呈现出如下互动过程：

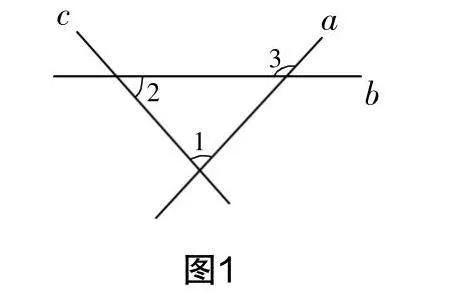
问题：如图1，分析图中各个角之间的关系.

师：想要判断各个角之间的关系，首先需要明确什么问题？

生1：应明确这三条线中，谁是截线，谁是被截线.

师：很好，那究竟怎么区分截线与被截线呢？

生2：如图2，通过最简单的图形来分析，对∠4，∠5来说，被截线为直线a，b，截线为直线c，∠4，∠5则是一对内错角……

生3：观察图2，可见直线a，b分别为∠4与∠5的边，直线c为∠4与∠5的公共边，因此截线与被截线在组成相关对应角中存在不同的功能.

此教学片段属于教学反思与调整的过程，教师在初次教学时虽然做了精心预设，但整个教学过程以教师的传授为主，学生自主探索的时间与机会较少，所以呈现出意料之外又是情理之中的败笔. 学生的作业反馈情况，给了教师闷头一棒. 据此，笔者及时反思并调整教学方案，主动与学生交流，发现学生的疑惑，并鼓励学生通过自主查阅资料与研究教材的方式答疑解惑.

这是在理解并尊重学生的基础上调整的教学策略，当学生自主总结出解决这一类问题的关键因素后，教师以一个实际问题启发学生的思维，引发学生的思考，使得学生在自主交流后总结出截线与被截线的概念. 因是自主探索而来的概念，学生自然而然地将此核心知识内化到相应的认知结构中，达到深层次理解与长时记忆的境界，为后续灵活应用做好铺垫.

开放教学时空界限，拓宽提问

途径

孔子曰：“不愤不启，不悱不发”，“愤”与“悱”是引发学生主动提出问题的基础. 学生一旦进入“愤”与“悱”的状态，则能感知到自身的已知与待实现目标之间存在的矛盾，进而产生困惑、焦虑与怀疑的心理状态，问题也在这种状态下自然生成［3］. 此时，教师要做的就是为学生提供充足的时间与空间，让学生有机会将问题用数学语言完整地表达出来.

虽说课堂是发展学生提问能力与核心素养的主要阵地，但绝非是唯一的渠道. 教师在课堂中并不一定要表现得无懈可击，更不需要解决所有的问题，而是根据课堂的时间、地点等环境条件来决定教学方式. 真正意义上的素质教育，并不是追求完美、不留遗憾的教育，而是给学生留有一定的时间与空间，让学生有机会自主提出并解决一些问题.

教师为学生提供充裕的探究时间与空间，鼓励学生走出家庭、课堂，面向社会，能让学生接触到更多的数学知识，开阔视野、开拓思维，逐渐形成用数学的眼光来观察现实世界的能力，并探寻出更多发现与解决问题的途径.

案例3 “轴对称与轴对称图形”的教学

本节课教学可分为以下几个步骤进行：①利用导学案进行预习，为课堂教学奠定基础；②课上组织学生进行合作交流，辨析轴对称与轴对称图形的概念与特征；③要求学生课后以小组为单位，收集身边的轴对称图形.

轴对称图形收集过程中，学生记录下如下问题：①那些看起来都一样的树叶，属于轴对称图形吗？②部分住宅的外观目测都呈轴对称，为什么呢？③身边有那么多物品都设计成轴对称图形，是否利于我们的使用呢？

轴对称与轴对称图形的学习过程中，学生容易出现思维受困且无法突围的情况，若学生得不到适当的引导，必然会影响其学习积极性. 教师要求学生课后自主探索生活中相关的实际物品，一方面能有效激发学生的探索热情，另一方面可为学生的思维困境解围，让学生从生活实际的角度对知识产生新的认识.

奥苏贝尔提出，将新知与学生的认知经验或原有认知结构中的概念相互联系是实现有意义学习的基础. 本教学片段，教师要求学生将“轴对称图形”这个新知与他们的生活实际相结合进行思考，促成了有意义的学习. 学生在探索过程中生疑、析疑、释疑，不断提升学力.

实践证明，为学生提供开放的教学环境是拓宽学习空间的主要渠道，学生通过自主探索让静止的教材内容变得灵动，彰显出数学知识的实际应用价值. 尽管初中阶段的学生还不能完全凭借自身已有的数学知识来解决很多生活或社会中的问题，但只要获得良好的提问能力与“三会”能力，则他们的未来可期.

总之，当下的初中数学课堂，教师不再是单纯的知识传播者，更是学习的引导者；学生也不再是知识的“接收器”，而是名副其实的探究者. 教师应在充分尊重学生的基础上，创设良好的学习环境，鼓励学生在知识的探索中形成细致观察与思考的习惯，主动提出高质量的问题，真正发展数学核心素养.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］胡军.捕捉最佳提问时机，让数学课堂更精彩［J］.数学通报，2014，53（6）：28-32.

［3］周心馨，张昆.珍视学生提问 促进教学相长［J］.高中数学教与学，2018（4）：16-19.