关于“全等三角形”的教学实践探究

［摘 要］ 教学“全等三角形”时，教师可采用“活动设计，过程探究”的方式，让学生实践操作，互动思考，逐步掌握其概念与性质. 研究者深入解读教材内容，设计教学环节，并开展课堂反思，提出相应的教学建议.

［关键词］ 全等三角形；活动；探究；教学

<D：＼数学教学通讯中旬＼2024数学教学通讯中旬（11期）＼2024数学教学通讯中旬（11期） c＼aa-1.jpg> 教学解读

“全等三角形”是八年级上册的重要教学内容，是对几何图形关系的深入探索，掌握全等三角形对学生后续学习十分重要. 本章节的知识重点是探索全等三角形的性质，知识难点是掌握两个全等三角形的对应边、对应角之间的规律，并能正确指出两个全等三角形的对应元素.

《义务教育数学课程标准（2022年版）》指出，要促进学生的全面发展，数学教学应遵循学生学习数学的心理规律. 因此，课堂上应从学生已有的生活经验出发，合理设计教学环节，让学生的知识水平与思维能力均得到提升.

探究三角形全等的主线是全等三角形的性质，教学过程中教师需要注意两点：一是合理进行图形变换，培养学生的直观想象能力；二是引导学生经历探究过程，包括观察、操作、归纳、总结等，提升学生运用思想方法处理问题的能力.

教学探究

基于上述内容解读与教学分析，实际教学中教师可采用“活动设计，过程探究”的方式，让学生参与活动互动，引导学生思考. 在整个探究过程中教师要注意合理设置问题.

1. 创设情境，课堂导入

活动一：生活情境引入

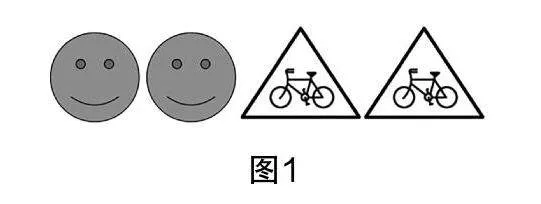
全等三角形的课堂导入可借助生活中的实物图，逐步过渡到“全等”知识. 教学中可呈现图1所示的图组，再设问思考.

问题1：每组图片有何共性特征，能否完全重合，请同学们做出猜想.

问题2：生活中还有相关的例子吗？

教学引导：学生通过观察组图中两图形的大小和形状，得出可以“完全重合”的结论. 在此基础上教师给出全等图形的概念，即“完全重合的图形”，后续再引导学生进一步列举生活中的例子，让学生理解“全等”的概念.

活动二：几何图形探索

完成生活情境引入后，逐步深入几何图形探索中. 教学中教师展示两组几何图形，如图2所示，让学生辨析是否为全等图形，明晰“全等”概念.

问题1：观察图2所示的两组几何图形，他们是不是全等图形？

问题2：根据对上述图形观察，你能得出怎样的结论？如果两个图形全等，它们的形状大小一定都相同吗？

教学引导：学生通过观察图形发现全等图形“大小、形状完全相同”，进而深刻理解全等三角形的核心概念，即“完全重合的三角形”.

教学建议：在全等三角形的教学引入阶段，教师应充分结合生活中的示例，创设情境，激发学生的探究兴趣，然后逐步过渡到数学中的几何图形. 在这一过程中，学生的思维集中到图形的“形状相同、大小相同”的知识点上，深刻理解“全等”概念，为后续探究全等三角形打下基础.

2. 实践交流，新知探究

基于现代教学理念，数学教学应注重动手实践，引导学生自主探索. 该环节是关于三角形全等特征的探索，在此环节中学生自主动手作全等三角形，在与同伴的交流总结中亲身感受全等三角形的几何特征. 具体教学过程分为两个阶段：实验发现、探究总结.

第一阶段：实验发现

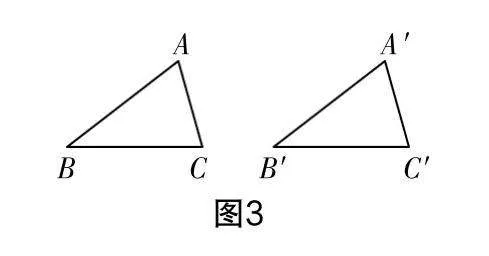
学生预先动手制作两个形状、大小均相同的三角形，于课堂演示两个三角形的重合情形，如图3所示.

思考1：观察这两个全等三角形，它们的对应边、对应角和对应点是怎样的？

思考2：“≌”表示全等符号，如何按照全等来书写两个三角形的全等关系？

思考3：若△ABC≌△A1B1C1，则他们的对应边是什么？∠A的对应角是哪个？如何来绘制图形？

教学引导：学生通过动手操作探究全等三角形的对应边、对应角，利用重合来初步发现其中的边角关系. 通过引入全等符号，将“全等关系”几何化，在此基础上学生完成全等三角形的知识构建. 对于两三角形的全等，需构建“全等关系”与“图形全等”之间的对应，让学生掌握两者的相互转换.

第二阶段：探究总结

在此环节，学生主要通过自主探究掌握全等三角形对应边、对应角的相等关系. 教师设置探究活动，并适时引导学生思考，让学生在讨论与合作中发现全等三角形的性质.

活动：将△ABC沿直线BC平移得到△DEF；将△ABC沿BC翻折180°得到△DBC；将△ABC旋转180°得到△AED，如图4所示.

思考1：上述各组变化中的两个三角形是否还全等？

思考2：根据上述操作，一个图形经过平移、翻折、旋转后，其形状、大小是否发生了改变？可以得出什么结论？

思考3：对于图5所示的一组全等三角形，△ABC≌△DEF，可以得出什么相等条件？

<D：＼数学教学通讯中旬＼2024数学教学通讯中旬（11期）＼2024数学教学通讯中旬（11期） c＼11-96.tif>[图5][B][C][A][E][F][D]

教学引导：学生在此环节中互动交流、合作探究，观察分析图形平移、翻折、旋转后的变化，得出“虽位置发生了变化，但形状、大小没有变化”的结论. 在此基础上，学生探寻两个全等三角形的对应元素，关注其对应边、对应角的关系，得出结论.

教学中教师完成知识总结，并指导学生规范书写，以上述图5的全等三角形为例，呈现如下全等性质.

知识总结：全等三角形的性质有对应边相等、对应角相等.

示例：△ABC≌△DEF.

对应边相等：AB=DE，AC=DF，BC=EF.

对应角相等：∠A=∠D，∠B=∠E，∠C=∠F.

教学建议：关于全等三角形性质的教学指导，教师应引导学生采用实践演示、自主探究的学习方式. 整个过程渗透类比思想，让学生感知知识间的有机结合. 操作探究中，学生应严格按照对应流程进行，经历观察、操作、归纳、总结等过程，完成知识总结归纳，提升数学思维能力.

3. 范例训练，应用强化

学生完成知识总结归纳后，还需通过应用来巩固知识，准确辨识图形，掌握全等三角形的性质. 教师要选取范例并将其合理变式，引导学生去探索分析，最终解决问题，初步培养学生的解题思维.

探究1：对应关系强化

问题1：如图6所示，△AOC≌△DOB，C和B、A和D是对应顶点，说出这两个三角形中相等的边、相等的角.

教学引导：学生思考如何变换可以使两个三角形完全重合，重合后的对应边和对应角是何种情形，从而得出结论，将△AOC翻折可以使△AOC与△DOB重合. 因为C和B、A和D是对应顶点，所以C和B重合，A和D重合.

相等关系：∠C=∠B，∠A=∠D，∠AOC=∠DOB；AC=DB，OA=OD，OC=OB.

探究2：知识灵活运用

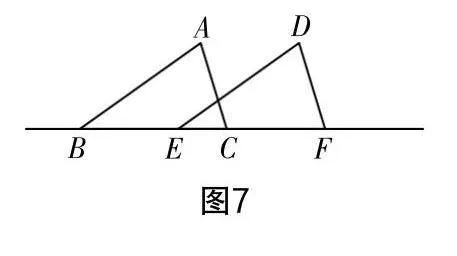
问题2：将△ABC沿直线BC平移，得到△DEF，如图7所示.

思考1：线段AB和线段AC的对应线段是什么？

思考2：若∠A=50°，∠B=30°，你知道其他各角的度数吗？为什么？

教学引导：结合平移知识来强化学生的图形辨识能力，进一步加深学生对全等三角形性质的理解. 教学中，学生先回顾全等三角形的性质，再结合平移过程确定三角形中的对应线段、对应角，灵活运用所学知识得出结论.

教学建议：范例训练与应用强化环节需要关注两点，一是问题设计的合理性，建议按照“知识强化—拓展分析”的思路来构建，覆盖核心知识，适度拓展思维；二是注意方法的讲解.

探究反思

1. 整合知识内容，明确教学重点

全等三角形是全等内容的起始课，其中的概念与性质是学生后续探究学习的关键，学生对其内容较为陌生. 教学中教师要深入解读教材，整合知识内容，在此基础上开展教学构建. 知识整合应注意两点：一是围绕教学大纲，结合教学任务，梳理知识的重点与难点；二是把握学情，结合章节前后内容，制定合理的教学规划，明确后续教学环节的重点. 另外，教学解读应注重学生情感素养方面的培养提升，全面覆盖，多重发展.

2. 以学生为本，探究操作实践

全等三角形的知识重点是概念与性质，与生活实际结合紧密，并具有一定的探究性、直观性. 教师应采用知识探究、操作实践的教学方式，以学生为本，围绕知识重点设计探究活动，让学生参与课堂讨论，经历多重探究过程，自主完成知识总结. 教师要合理设计问题，引导学生思考，从生活实例中发现全等，关注几何全等的特征，逐步完成全等性质总结. 在整个过程中教师要关注学生的思维变化，根据学情来适度调整.

3. 渗透数学思想，培养学科素养

培养学生的“直观想象、推理论证能力”是本章节教学的关键，教师要关注学生在活动中所表现的情感、态度，借助几何全等的知识探究来加以培养. 具体教学中，教师应在活动设计中逐步渗透思想方法，例如从“生活实例”到“几何图形”中渗透模型思想；“几何变换”中渗透动态思想；“类比探究”中渗透类比思想；整个推理分析过程中培养学生的解析思维；问题解读分析过程中合理引入数形结合思想. 通过直观几何教学来全面提升学生的思维水平，强化学生的核心素养.

结束语

教学“全等三角形”时，教师要注意解读教材内容，明确教学任务，合理安排教学流程. 整个教学以活动探究为主，让学生经历探究过程，在活动中互动交流、思考分析，掌握知识的同时提升综合能力.