核心素养背景下预设与生成共生的课堂教学探索

［摘 要］ 核心素养背景下的数学课堂教学，不仅要做好精心预设，还要顺应学生的思维，做到点滴生成，达到预设与生成共生的目的.文章以“一次函数图象”的教学为例，分别从教学内容、教学目标与学情三个方面展开分析，并从如下四个方面展开教学设计与分析：创设活动情境，趣味融合；设计探究活动，突破难点；借助辨析活动，完善认知；鼓励多元编题，深度参与.

［关键词］ 预设；生成；一次函数

新课教学属于从已知向未知领域探索的过程，教师做好课堂的预设，不仅能促进课堂的生成，还能让学生萌生创新意识，此为发展核心素养的基础. 作为一线教师，应充分保护学生的思维，尊重学生在课堂中提出的每一个问题，让课堂在妙手偶得之中动态生成. 本文以一次函数图象的教学为例，具体谈一谈如何基于学生的最近发展区设计教学活动，帮助学生搭建良好的学习平台，促使学生实现自我挑战与突破，发展数学核心素养.

教学分析

1. 教学内容分析

一次函数图象的教学属于函数图象教学的起点，本节课属于函数教学的延续，又高于原来对函数的探索，是函数图象与性质的垫脚石. 尤其是“描点法”的探索，对后续学习具有决定性意义. 在课堂中，教师带领学生亲自动手描点、画图，不仅能帮助学生进一步感知数形结合思想的重要性，还能促使学生对函数图象与解析式的对应关系产生深刻理解，由此揭露函数图象是研究函数问题的重要依据.

2. 教学目标设定

（1）亲历“描点法”活动，积累活动经验.

（2）多感官系统参与活动过程，感知直线上的点坐标与一次函数解析式之间为一一对应的关系，提炼数学思想.

（3）获得用两点法构建一次函数图象的能力，并能自主求解一次函数图象和坐标轴形成的交点坐标.

（4）通过课堂学习感知函数图象探索的重要性与必要性，形成良好的应用意识，体会自变量取值与一次函数图象的关系. 初步形成直观想象、数学抽象与逻辑推理等素养.

3. 学情分析

之前学生已经了解过函数有三种表达方式，因此大部分学生能理解图象所表达的是变量间的关系. 但什么是一次函数图象呢？对于这一点，学生还不够清晰. 同时，学生还缺乏画一次函数图象的经验. 所以，在新课教学之前，教师要带领学生分析：函数图象概念究竟是怎样获得的？如何既快又准地画出一次函数图象？从什么角度理解函数图象与解析式之间的对应关系与融合关系？

基于以上分析，笔者在教学之前认真研读过教材、剖析过学生，结合实际情况将教学目标渗透到各个教学环节中，让学生在精心预设中感悟知识的形成与发展，为课堂的生成奠定基础.

教学过程设计

1. 创设活动情境，趣味融合

趣味性的导入模式可提高学生对教学内容的探索欲，让学生在趣味融合的环境下以饱满的精神进入对新知识的探索中. 本节课的教学主题为“一次函数图象”，主要反映的是两个量之间一一对应的关系. 因此，教师可以从生活实际中择取一些具有这种特征的现象，以驱动学生的探究力，让学生学会用数学的眼光观察世界.

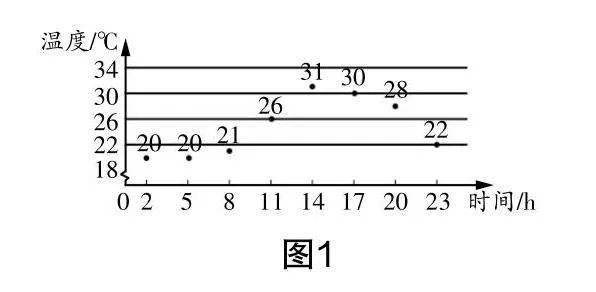
问题1：如图1为某地某天的气温变化情况图，通过对这张图的观察，可获取一些什么信息？

生1：这一天14时的温度高达31 ℃，早晨2-5时温度仅有20 ℃.

生2：这一天的温度从早晨到中午逐渐上升，14时到达最高峰，而后又缓慢下降.

……

师：你们观察得很仔细，从这个活动来看，图象能将一些生活现象直观地展示出来，那么图象是由什么组成的？

生3：多个点组成的.

设计意图 对于这个年龄段的学生来说，看图说话更能调动感官系统. 一次函数图象是学生初次接触的函数图象，学生对一次函数图象虽然陌生，但观察气象图分析问题却是学生拿手的. 在此环节中，通过师生共同讨论与总结，学生自主提炼出“由点组成图象”的基本事实，这一发现成功揭露了一次函数的本质，学生也由此明确了图象中每一个点均有自己的实际意义，如可被表示、被读取等. 因此，创设丰富的情境，不仅让学生主动进入知识的探索中，还感知数学与生活的关联性，体会生活素材是辅助数学学习的重要资源.

2. 设计探究活动，突破难点

精心预设问题是引发学生深入探究的关键. 学生在问题的引领下，通过自主思考与合作交流对一些现象进行深入探索，不仅能突破自身原有的认知，还能击溃教学难点的壁垒，达到深入学习的目的. 用数学思维思考世界是探究的根本，学生在探究过程中不断发现、提出、分析与解决问题，获得“四能”. 由此，本节课的探究在教师的精心预设中展开.

问题2：一次函数y=x的图象怎样画？

师生活动：根据第一个环节的探索结论，可知点组成了图象. 因此，想要画一次函数的图象，首先要找到函数图象中的点，然后建立平面直角坐标系，将点描在坐标系内，如点A（1，1），B（2，2），C（3，3），…均位于坐标系内的第一和第三象限的角平分线上. 反之，也可猜想处于第一和第三象限的角平分线上的点的纵、横坐标相等，借助几何画板论证这个猜想. 互动最后，要求学生自主应用描点法展示一次函数y=x+2的图象.

随着活动的开展，学生总结出如下三点感悟：①正比例函数图象过原点，是一条直线；②一次函数y=x+2的图象，是将y=x的图象向上平移两个单位长度的图象；③一次函数y=x+2的图象同样为直线.

设计意图 由浅入深的探索活动，可激活学生的思维. 此环节，若直接要求学生画一次函数y=3x+1的图象，会因为问题的起点过高，导致学生难以理解“点在一条直线上”. 带领学生参与一次函数图象的绘制过程，循序渐进地加大难度，可让学生从真正意义上知其然且知其所以然，由此构建完整的认知结构.

结合学生已有的认知经验，与正比例函数进行类比教学，让学生感知特殊到一般的探究过程，为构建一般性的认知规律奠定基础. 同时，通过函数表达式、点坐标、角平分线等知识的应用，实现了“图与式”的双向转化，发展了学力.

3. 借助辨析活动，完善认知

问题3：请将一次函数y=-5x+20的图象画出来.

关于这个问题，大部分学生会受“描点法”思维定式的影响，选择描点连线来画图，这种方法并没有原则性问题. 其实解决本题还有更简便的方法，但学生只会用“描点法”来画图，只能说学生对一次函数图象为直线的理解还不够，到实际应用时束手束脚. 为了启发学生的思维，教师在此处不需要给予太多引导，而是给学生留充足的时间与空间用“描点法”进行画图，同时借助几何画板将点连接起来形成直线，由此进一步强化学生对“一次函数图象的本质为一条直线”的认识.

师：除了“描点法”外，是否还存在其他更便捷的画图方法？

众所周知，连接两点即可形成一条直线. 鉴于一次函数图象为直线的规律，遇到此类问题可先探寻出两个点，将这两个点连接起来形成一次函数的图象. 此为课前教师精心预设的过程，学生在此环节积极主动地参与，凸显了学习的主动性，整个教学活动在精心预设的背景下更加井然有序.

师：接下来，请大家辨析下列两个问题.

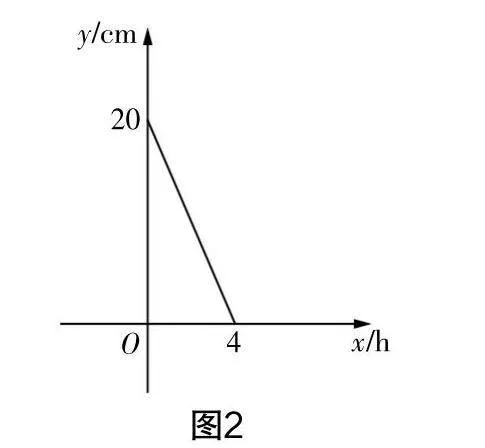
（1）20厘米长的蜡烛，在燃烧的状态下，每小时短5厘米，那么剩下的长度y与燃烧的时间x之间有一种函数关系，尝试将这种关系画出来.

如图2，学生自主画图，并提出在这个问题中，函数图象并非一条直线，而是一根线段. 由此也让学生明白，在画函数图象时，不仅要关注建立坐标系、取点、描点等问题，还要关注自变量的取值范围问题.

（2）某平台预测本年度某产品在前四个月需投入广告费y和月份x之间存在的函数关系为y=-5x+20，该函数图象是否为直线？

师生活动：如图3，经探索发现，在该情境背景下y=-5x+20的图象为有限个点.

设计意图 以上两个问题情境主要是为了引导学生自我辨析，以形成递增式问题链，学生基于自身已有的认知经验展开探索与分析，不仅逐步探寻出问题所蕴含的数量关系，还对函数图象有了更清晰的理解，建构了完整的函数模型. 随着探索的深入，学生明确认识到不同情境下的问题可能会用到相同的模型. 辨析活动的开展，犹如给学生平静的心湖内丢进一颗石子，荡起阵阵涟漪. 学生基于认知冲突逐层细化、分析，对不同背景下的函数图象产生深刻理解，为完善认知结构夯实了基础.

4. 鼓励多元编题，深度参与

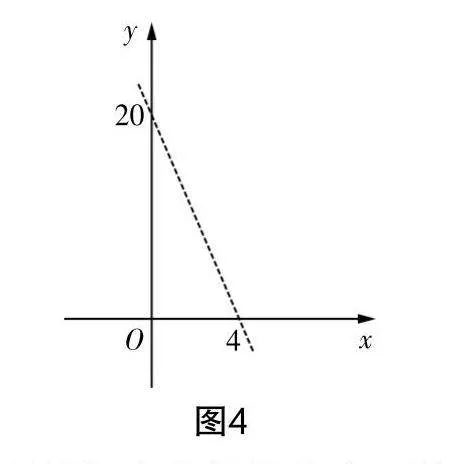
问题4：要求学生自主提一些问题，确保问题与一次函数y=-5x+20相关.

此为一个开放性问题，每一个学生的生活经验与对事物的认知不一样，提出的问题自然不一样. 多元编题模式的开展，有效避免了教师“注入式”空洞说教的弊端，学生基于手、脑、口的协作挖掘潜能，积累学习经验，提炼数学思想方法，为获得“特殊点”做铺垫.

如图4，此为学生所画图象，教师要求其他学生说一说从这幅图中发现了些什么，借助该图可解决一些什么问题，等等.

引导学生将教学内容巧妙地进行转换，形成具有实际意义的问题，可促使学生学会用数学的语言来描述现实世界，提升“四能”.

师生活动：结合直线上一些特殊的点，如与纵、横轴相交的点，进一步探索特殊坐标，并对直线和坐标轴构成的图形面积进行分析. 在此基础上，与学生共同探讨如下例题，帮助学生进一步巩固所学内容，以从真正意义上提升学力，发展数学核心素养.

例1 已知点A（0，20），B（4，0），C（2，10）是平面直角坐标系内的三点，分析它们是否处于同一条直线上.

师生活动：分析发现y=-5x+20为直线AB所对应的函数解析式，想要确定点A，B，C是否共线，只要探索点C是否处于AB所在直线上. 一旦明确了解题思路，就很容易获得结论. 将x=2代入直线AB的函数解析式y=-5x+20中，计算可得y=10，由此确定点C位于直线AB上. 除了这种方法外，还可以通过“描点法”进行验证.

例2 点P（2a，-6a+8）是不是函数y=-5x+20图象上的一点？

师生活动：对于一点是否位于函数图象上，可以用“描点法”或“计算法”进行分析判断. 为了让学生一目了然，教师带领学生通过观察几何画板的演示，明确不论a取值多少，只要是实数，点P均处于y=-3x+8上，函数y=-5x+20的图象与y=-3x+8的图象的交点为（6，-10），因此确定唯有a=3时，点P位于函数y=-5x+20的图象上.

设计意图 编题活动将教学内容渗透在问题中，学生通过对隐含知识的挖掘，进一步深化对一次函数图象的理解. 此环节，在教师的精心预设下，学生的思维与知识深度融合，进一步优化了学习能力，获得了常规的解题思路，课堂在精心预设中有机生成.

教学思考

本节课基于学生已有的认知经验而展开，如气温图的应用，就是将学生带入一个熟悉且开放的情境，让学生基于认知冲突进入探索状态，课堂随着教师的精心预设逐渐进入正轨. 辨析活动中关于函数图象的绘制也是基于学生已有的生活经验而设计的，并对学生的实际需求精准定位，不仅营造了良好的学习氛围，还从真正意义上促使课前预设与课堂生成的互动共生.

总之，预设与生成之间为相伴相生的关系，课堂因为有了教师的精心预设，才让生成更自然. 事实证明，预设与生成互动共生的环境是帮助学生厘清知识脉络的载体，课堂因有明确的导向而充满智慧.