核心素养背景下问题引领数学教学的研究

［摘 要］ 问题作为数学的心脏，在课堂中具有举足轻重的作用. 核心素养背景下的复习教学，该如何应用问题启发学生的思维，发展学生的数学能力呢？研究者以“全等三角形”的复习教学为例，分别从“并列式问题回顾旧知，引出新知”“递进式问题梳理方法，拓展策略”“探索式问题提升能力，激活思维”三方面展开教学与分析，并谈几点思考.

［关键词］ 问题；全等三角形；复习

《义务教育数学课程标准（2022年版）》对义务教育阶段学生需要掌握的核心素养做了新的阐释. 问题作为数学的心脏，对教学具有导向作用. 如何以问题为基础，通过不同形式问题的设置启发学生的数学思维，发展学生的核心素养呢？这是笔者近年来一直在探索的话题，在此以“全等三角形”的复习教学为例，具体谈谈问题导学提升复习成效的主要措施.

教学简录

1. 并列式问题回顾旧知，引出新知

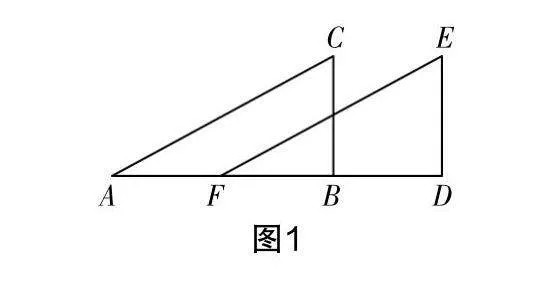
如图1，已知△ABC与△FDE全等.

问题1 观察图1，可初步获得哪些结论？

生1：结合题设条件可知AB=FD，BC=DE，AC=FE.

师：很好！根据题设条件与图示除了知道几组相等的线段之外，还可获得什么结论？

生2：还可以从角去分析，如∠ACB=∠FED等.

生3：还可以从平行的角度发现AC∥FE.

生4：我还发现AF=BD.

师：非常好！你们是以什么为依据分别获得以上结论的？

生4：从全等三角形相对应的边、角均相等的定理而得.

（板书：全等三角形的性质）

设计意图 此问意在引发学生对旧知（全等三角形的性质）的回顾，学生通过对问题1的分析，从已有的认知体系中提取了全等三角形的性质，为接下来进一步深入复习奠定基础. 同时，低起点的问题有效激活了学生的思维，让全体学生都积极地参与到课堂中来，使得每个认知水平层次的学生都从简单问题中获取了学习信心，为整个复习奠定了良好的基础.

问题2 我们该如何发现全等三角形对应的边与角呢？

生5：从题设条件△ABC≌△FDE可以发现两个全等三角形所对应的边和角，如AC边与FE边相对应.

师：不错，从数学符号语言出发可以探寻到全等三角形所对应的边，还有其他不同的探寻方法吗？

生6：也可以通过对三角形的平移，获得相应的边、角相等.

师：以上两种方法均能发现全等三角形相对应的边和角，我们在解决实际问题时，可结合题设条件灵活变通，从便捷的角度发现边、角对应相等的条件或结论.

（板书：找对应——方法点）

问题3 关于AF=BD，AC∥FE的结论，是否也能应用以上两种方法直接获得？

生7：不行，这两个结论需要经过转化才能获得，如AF=BD需结合全等三角形的性质，先获得AB=FD将这两条线段分别减掉公共线段BF，可得AF=BD.

师：不错，这位同学将直接的量，即相等的边AB=FD转化成间接的量线段AF=BD，充分体现了数学学科中转化思想的灵活性.

设计意图 此问意在帮助学生提炼常见的数学思想——转化思想，为后续解题奠定基础. 当然，这也是发展数学核心素养的体现.

效能分析 复习需遵循由浅入深的过程，学生在之前对全等三角形的性质已经有所了解，但由于间隔了一段时间有所遗忘. 教师借助一组并列式的问题引导学生重构知识，让学生在自然的状态下勾起对旧知的回顾，而后通过直接量与间接量的转化，有效提炼了转化思想与技能. 整体来说，这种并列式的问题从对知识与技能的梳理、整合与重组方面启发了学生的思维，激活了学生的认知，为帮助学生构建完整的知识网络奠定了基础.

2. 递进式问题梳理方法，拓展策略

问题4 如图1，已知△ABC与△FDE，若想确定这两个三角形为全等的关系，需添加几个条件？依据是什么？

生8：需添加三个条件，依据为SAS，ASA，SSS，AAS.

师：所添加的条件中，有一组什么条件是必备的？

生9：“一组对应边相等”的条件必不可少.

设计意图 此为判定三角形全等条件的梳理过程，引发学生对全等三角形的判定定理（SAS，ASA，SSS，AAS）产生回顾，尤其关注到不论用哪种方法判定两个三角形全等，少不了一组对应边相等的支持.

问题5 如图1，若想判定Rt△ABC与Rt△FDE为全等的关系，需添加几个条件？为什么？

生10：仅需添加两个条件，虽然图形没有发生改变，但题设条件中出现了“直角三角形”的条件，可知这两个三角形中，有一对对应的角相等.

师：很好！虽然还是同一幅图，但题设条件发生了改变，那么对问题的分析同样要从新的角度去思考，如此来看，题设条件信息对结论具有决定性作用. 在已有条件的基础上，给题目添加了BC=DE这个条件，想要确定△ABC≌△FDE，还需增加什么条件？

生11：可增加AB=FD.

师：说说为什么增加了AB=FD这个条件后就能确定△ABC≌△FDE？

生11：通过题设条件来分析，已知“BC=DE”“∠ABC=∠FDE=90°”，即存在一组对应边与对应角相等，结合三角形全等“SAS”的判定法，添加AB=FD即可.

师：本题除了添加这个条件之外，还存在其他方法吗？

生12：还可以从“ASA”的角度出发，添加∠C=∠E；从“AAS”的角度出发，添加条件∠A=∠EFD；从“HL”的角度出发，添加条件AC=FE.

生13：还可以添加AC∥FE或AF=BD.

师：很好！谁来说说AC∥FE或AF=BD的理由.

生14：根据AB=FD，可知添加AF=BD亦可；根据∠A=∠EFD，可知添加AC∥FE亦可.

设计意图 将AF=BD转为AB=FD，可得△ABC≌△FDE；根据AC∥FE，可得∠A=∠EFD，可确定△ABC≌△FDE. 这两种情况都体现了数学转化思想的应用，即将间接的量转化成直接的量.

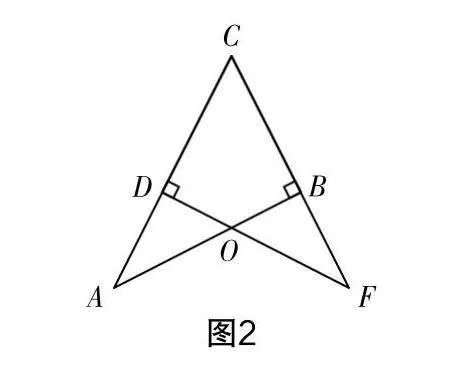
问题6 如图2，已知Rt△ABC与Rt△FDC中的BC=DC，若想确定△ABC≌△FDC，需添加几个条件？

生15：仅需添加一个条件即可.

生16：我认为不需要添加任何条件，结合“ASA”判定法，根据∠CDF=∠CBA（直角），∠C=∠C，BC=DC，就能获得△ABC≌△FDC.

师：很好！显然∠C为题中的隐含条件，除此之外，图形中常见的隐含条件还有哪些？

生17：如公共角、公共边、对顶角等，都可作为隐含条件使用.

效能分析 全等三角形的新知授课时，不少学生就存在一些易错点. 此环节，教师将三角形的条件进行了微调，即以直角三角形作为条件呈现，意在引发学生关注文本中的隐含信息，而后添加条件BC=DC，将认知性问题逐渐推向方法性问题，学生结合条件自主确定全等三角形的判定方法，进一步强化了转化思想的应用. 随着图形的变化，又将问题转化成策略性问题，引发学生关注隐含信息而提升解题策略. 这一系列递进式问题的引导，将知识、方法与策略有机地融合在一起，让学生自主发现自身的不足，有效完善了学生的思维，提升了解题能力.

3. 探索式问题提升能力，激活思维

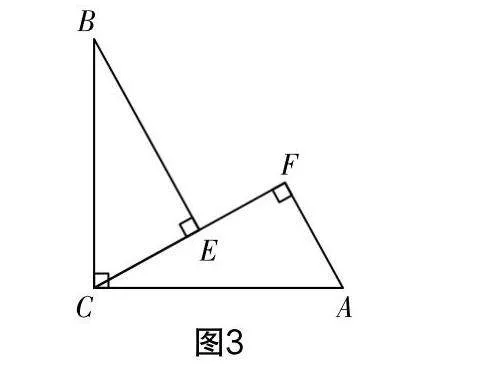
如图3，在△CBE和△ACF中，∠CEB=∠AFC=90°，∠BCA=90°，AC=BC.

问题7 分析线段AF，BE，EF之间存在什么数量关系？理由是什么？

生18：EF+AF=BE，我用尺子分别测量了这三条线段的长度，发现AF=1.4 cm，BE=2 cm，EF=0.6 cm.

师：这不乏为一种好的方法，该结论是否正确呢？请大家求证.

生19：想要求证该结论，只要证明△BCE≌△CAF即可.

师：本题已有的条件为AC=BC以及∠CEB=∠AFC，如何确定这两个三角形是全等的呢？

生20：根据∠BCA=90°，可知∠BCF+∠FCA=90°. 因为∠BEC=90°，所以∠BCF+∠EBC=90°. 所以∠FCA=∠EBC. 根据“AAS”，可得△BCE≌△CAF. 从而得到EF+AF=BE.

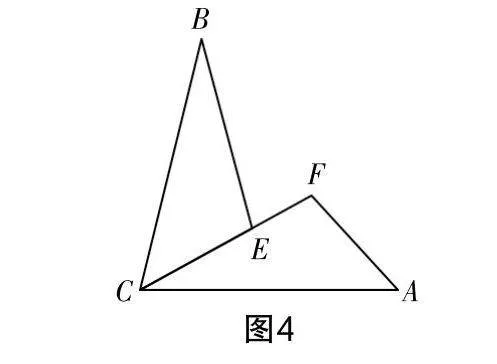
问题8 如图4，△ACF与△CBE中有CA=CB，∠BEC=∠CFA=∠α，请添加一个与∠α，∠BCA相关的条件，让AF+EF=BE成立.

生21：初步猜想∠BCA+∠α=180°，理由是我用量角器分别测得∠BCA与∠α的度数，发现这两个角相加的值为180°.

师：不错，还有其他方法吗？

生22：根据图3中∠ACB=90°与∠BEC=∠AFC=90°的条件，猜想∠BCA和∠α之间存在两种关系，即两个角相等或相加的值为180°. 本题显然∠BCA与∠α并不相等，那我猜想∠α+∠BCA=180°.

师：很好，应用数形结合思想进行猜想，这是一种常见的猜想方法. 关于这个猜想如何证明呢？

生22：仅需证得△BCE≌△CAF即可.

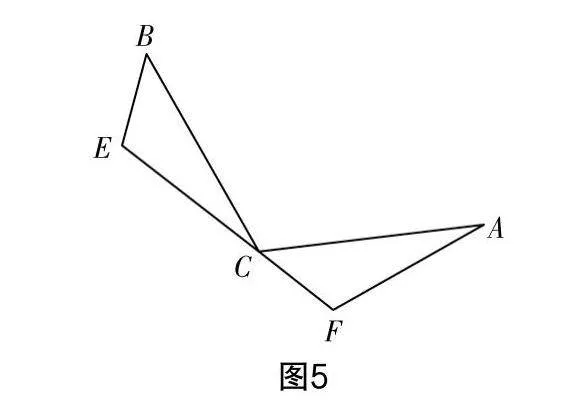
问题9 如图5所示，在△ACF和△CBE中，已知AC=BC，∠CEB=∠AFC=∠α，∠α=∠BCA，猜想线段AF，BE，EF之间存在什么样的数量关系.

生23：EF=AF+BE.

师：纵观图3、图4、图5，我们发现图形在不断地发生改变，其中什么一直没有变化？

生24：每一幅图中都存在两个三角形全等.

师：很好！我们在解决实际问题时，就要学会从问题中发现其本质，像这一类题目就需要从全等三角形的角度去分析与思考.

效能分析 学生的思维能力与探索能力随着问题的深入而提升. 此环节，第一个问题的设计，意在引发学生梳理全等三角形定理应用的基本流程，鼓励学生要勇于猜想；在此基础上，通过对图形的变化引出图4，让学生学会结合条件实施猜想与验证；随着图5的展现，学生的思维也从探索层面逐渐上升到了思维层面. 问题前后类比有效提升了学生的问题意识与解题能力，学生在探索中不仅学会了从不同角度与层次分析、解决问题，还进一步完善了思维品质，为发展数学核心素养加大了筹码.

几点思考

1. 以问完成学与构

问题是引领复习教学的基础，也是学生在课堂中思考的方向. 本节课从全等三角形的定义、性质、判定等知识出发，借助问题建立知识结构、技能方法与数学思想等. 如第一个教学环节，学生就在问题的引领下通过对旧知的回顾，初步建构了全等三角形的知识结构网络，而后随着问题的启发，学生不仅探寻出证明全等三角形性质的基本方法，还构建了发现全等三角形性质的基本技能.

教学的第二个环节，随着问题的解决，学生自主建构了一幅判定两个三角形为全等关系的方法结构；第三个教学环节，随着图形的变化，促使学生进一步提炼数学思想，为后续解决更复杂的综合性问题奠定基础. 问题是促使学生自主建构，形成良好知识技能与方法的纽带，是促使学生积极思维的基础，对培养学力、提升学生的思考能力，顺利达成学与构的目标并进一步挖掘潜能具有重要意义.

2. 以问体现明暗线

明、暗两条线往往是构成复习课的基础. 本节课，明线是附着于问题之上的知识与技能；暗线为贯穿于问题中的思想方法. 由全等三角形的“性质—判定—应用”，逐层深入、丝丝入扣，明暗线始终贯穿问题，暗线依附于明线，而明线又服务于暗线，两条线互相缠绕、相得益彰.

本节课的两条线均以学生的实际认知水平为出发点，通过问题串联，具有一定的探究性. 教师将学习的主动权交给学生，促使学生在个体独立思考与合作交流中不断提升思维，提炼思想方法，发展核心素养.

3. 以问展示引和评

新课标强调数学课堂离不开教师适时的引导与即时的评价. 捕捉学生在解题过程中释放出来的信息，可给予学生合理的评价与引导，这是对学生思维的肯定，又是提升学生思维能力的基础. 课堂中，教师对学生的回答不断以“很好”“不错”等词语进行肯定，有效激发了学生的学习信心. 学生在充满人文关怀的课堂中，不断提升自己的问题意识与思维能力.

总之，在以问题为导向的课堂中，处处彰显了“以生为本”的理念. 然而，本节课还存在一些不足之处，如课堂涉及的知识仅限于全等三角形，其实复习教学应该将学生已经学过的知识综合在一起，更能提升学生的思维能力. 比如勾股定理则可有机地融入本节课的问题中，以促使学生进一步构建完整的知识结构，提升解决综合性问题的能力.