基于改进和声算法的叉车车间布局研究

摘 要：制造企业在生产效率低的原因之一是车间布局问题，因此科学合理的布局对制造企业来说尤为重要。以往车间布局多采用经验布置，存在一定不足，本文以搬运成本最小和非物流关系最大为目标函数建立模型，并选择改进和声搜索算法对模型进行求解，得到最终布局方案，最后通过Flexsim软件对改进前、后的车间进行建模仿真，结果表明改进的和声算法在车间布局应用中取得了良好效果。

关键词：改进和声算法；车间布局；SLP；多目标优化；Flexsim

中图分类号：TH 181" " " " 文献标志码：A

全球经济一体化和制造业飞速发展对我国制造业的发展既是一种机遇，也是一个巨大的挑战。在制造业发展过程中，生产和物流的联系越来越紧密，优化生产物流的关键是合理的设施布局。合理的设施布局可以提高企业的生产效率并节约成本[1]。以往学者采用不同的优化算法与SLP方法结合，取得了良好效果，例如邓兵等[2]采用SLP与遗传算法相结合，改进了原有布局。丁祥海等[3]针对设施布置中存在的设施形状不固定问题，提出了一种将GA算法与退火算法相结合的动态求解方法，显著提高了设施利用率。

上述研究极大丰富了车间布局的相关理论，但是对于不同设施布局，其采用的目标函数和算法也具有极大差异，其中一些算法存在一定的局限性，容易陷入局部最优，因此本文采用一种改进的和声搜索算法，对车间进行布局优化，并用仿真软件验证其有效性。

1 模型建立

1.1 目标函数

在目前的设施布局规划问题中，单一目标函数的局限性不能满足车间布局优化的多样化需求，因此需要建立多目标函数模型。本文以最小搬运成本C和最大化非物流关系M为目标函数，构建车间布局模型。其中最小化搬运成本如公式（1）所示，其由作业单位间的搬运成本、搬运距离和搬运量的乘积计算得出；最大化非物流关系如公式（2）所示，其主要由作业单元间的非物流关系的紧密程度和关联因子计算得出。

式中：n为生产单元的数量；cij为生产单元间i与j间的搬运成本；fij为作业单元i与j间的搬运量；dij为作业单元i与j间的距离，由曼哈顿距离表示，dij=|xi-xj|+|yi-yj|。

式中：n为车间中的作业单元数；Tij为作业单元i与j间的非物流关系的紧密程度；Bij为作业单元i与j间的非物流关系等级与距离的关联因子。

为了便于处理，将多目标函数转换为单目标函数，由于2个函数的量纲不同，因此需要对其进行标准化处理，分别如公式（3）、公式（4）所示。

式中：dmax为任意2个生产单元间的最大距离；cij为生产单元间i与j间的搬运成本；fij为作业单元i与j间的搬运量；dij为作业单元i与j间的距离；n为车间中的作业单元数。

式中：n为车间中的作业单元数；Tij为作业单元i与j间的非物流关系的紧密程度；Bij为作业单元i与j间的非物流关系等级与距离的关联因子。

将公式（3）和公式（4）结合构成单目标函数，并引入加权因子f1和f2来调整2个目标函数所占的比重，其中f1+f2=1，转化后的目标函数如公式（5）所示。

minX=f1C1-f2M1 （5）

式中：f1为搬运成本所占权重；f2为非物流关系所占权重。

1.2 约束条件

1.2.1 边界约束

为保证目标函数得以求解，需要设置相应的约束条件，对车间的边界进行约束，即任意2个生产区域的距离应当始终小于边界区域，如公式（6）、公式（7）所示。

式中：xi和xj分别为任意作业单元i和j的X轴中心坐标；Li和Lj为作业单元i和j的长度；L为该车间的长度。

式中：yi和yj为任意作业单元i和j的Y轴中心坐标；Wi和Wj为作业单元i和j的长度；W为车间的宽度。

1.2.2 间距约束

除边界约束外，为保证任意2个生产区域间没有重叠，不同的生产区域间应当保留一定距离，间距约束如公式（8）和公式（9）所示。

式中：xi和xj分别为任意作业单元i和j的X轴中心坐标；Li和Lj为作业单元i和j的长度；s为作业单元i和j间的最小间隔距离。

式中：yi和yj为任意作业单元i和j的Y轴中心坐标；Wi和Wj为作业单元i和j的长度；s为作业单元i和j间的最小间隔距离。

2 改进和声算法设计

和声搜索算法是一种基于音乐演奏和声原理的智能算法，和声搜索算法产生于音乐创造过程中，模拟了音乐演奏中乐师调整每个乐器音调的，最终使乐器达到和声最美的状态[4]。和声算法解决的问题主要是离散问题优化和非线性问题，而车间布局问题正是常见的离散优化问题，但是标准的和声算法容易受声库、取值概率和微调概率的影响[5]。为解决该局限，本文提出一种结合遗传算法、改进和声算法的新方法，具体实施步骤如下。

2.1 初始化和声库

2.2 确定适应度函数

在遗传算法中，种群中个体适应度越大，说明该个体越优秀。由于前提假设的是求最小值，因此设置适应度函数如公式（10）所示。

2.3 设定编码方式

本文编码采用实数编码方式，实数编码的样式为[m1，m2，…，mn]，表示从车间的左下角开始，依次沿着X轴布置作业单位，如果同一行作业单位的长度之和超过车间总长度，就自动换行，得到最终布局图。

2.4 创作新和声

创作新和声需要先初始化和声记忆库，在决策变量Xe中随机生成HMS个和声x1，x2，…，xHMS，再将和声放入和声库HM。生成新和声的方式如公式（11）所示。

式中：新和声变量xe'以HMCR的概率选择[0，1]中的任意一个值，反之，1-HMCR的概率选择HM外的任意一个值；rand1为均匀分布在[0，1]的随机数。

2.5 更新和声库

如果新的和声xe'来自HM，就对其进行音调微调，随机生成均匀分布在[0，1]的随机数rand2。当rand2lt;PAR时，将遗传算法的变异代替和声算法的微调带宽，反之不调整。具体操作如下所述。

2.5.1 选择操作

以个体适应度为依据选择个体进行遗传操作，从旧的种群中使用轮盘赌法选择适应度高的染色体，为以后染色体交换、变异并产生新的染色体做准备[6]。其中染色体被选中的概率Pr如公式（12）所示。

式中：xe为种群中第e个染色体；f（xe）为第e个染色体的适应度值；∑ f（xe）为种群中所有染色体适应度值之和。

2.5.2 交叉变异

交叉是指在自然界繁殖中由染色体的交换组成新的品种，遗传算法中的交叉运算是指根据一定的交叉概率Pc对2个相互配对的染色体交换部分基因，从而形成新的个体[7]。本文将多点交叉作为交叉算子，变异算子可以维持染色体的多样性，提高算法的局部搜索能力，其基本思想如下：在编码长度内随机生成2个位置a和b，对2个位置间的基因进行逆序变换，从而增强和声搜索算法的整体寻优能力。

3 算例分析

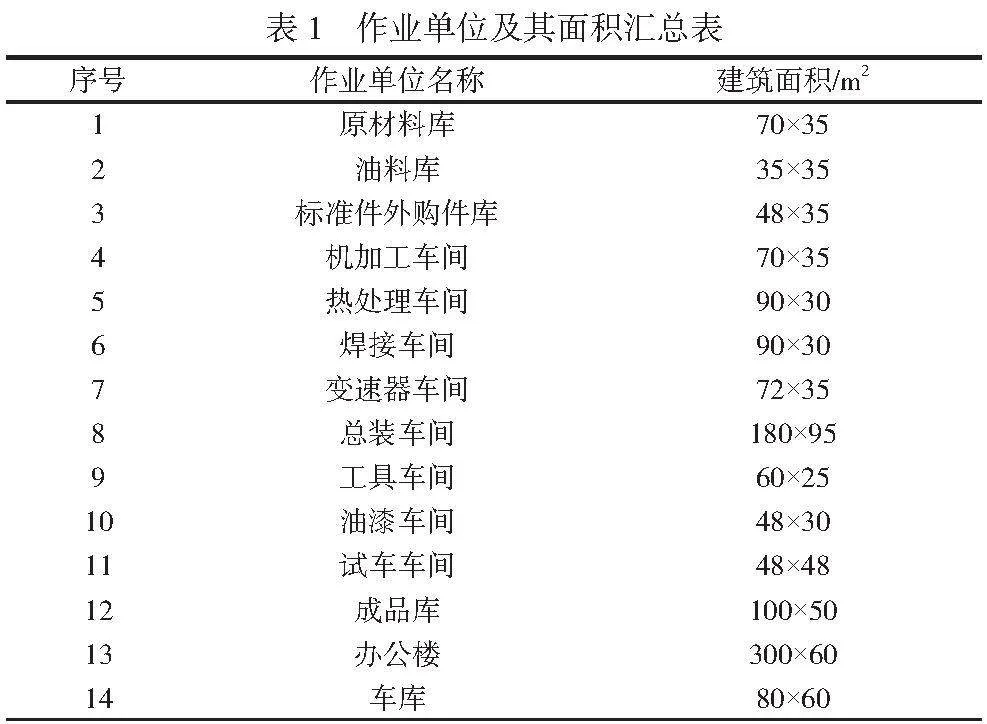
以A企业为例，已知该企业的生产车间共有14个区域：1原材料库；2油料库；3标准件外购件库；4机加工车间；5热处理车间；6焊接车间；7变速器车间；8总装车间；9工具车间；10油漆车间；11试车车间；12成品库；13办公楼；14车库。拟布局的车间长600m，宽300m，各单位所占面积见表1。

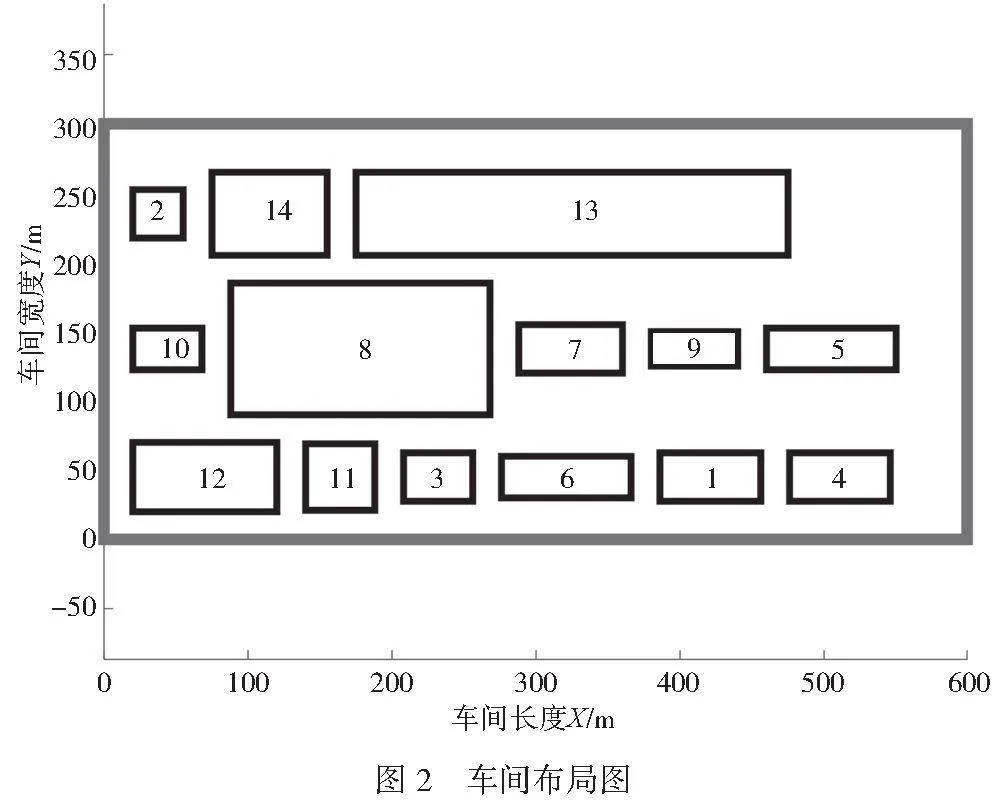
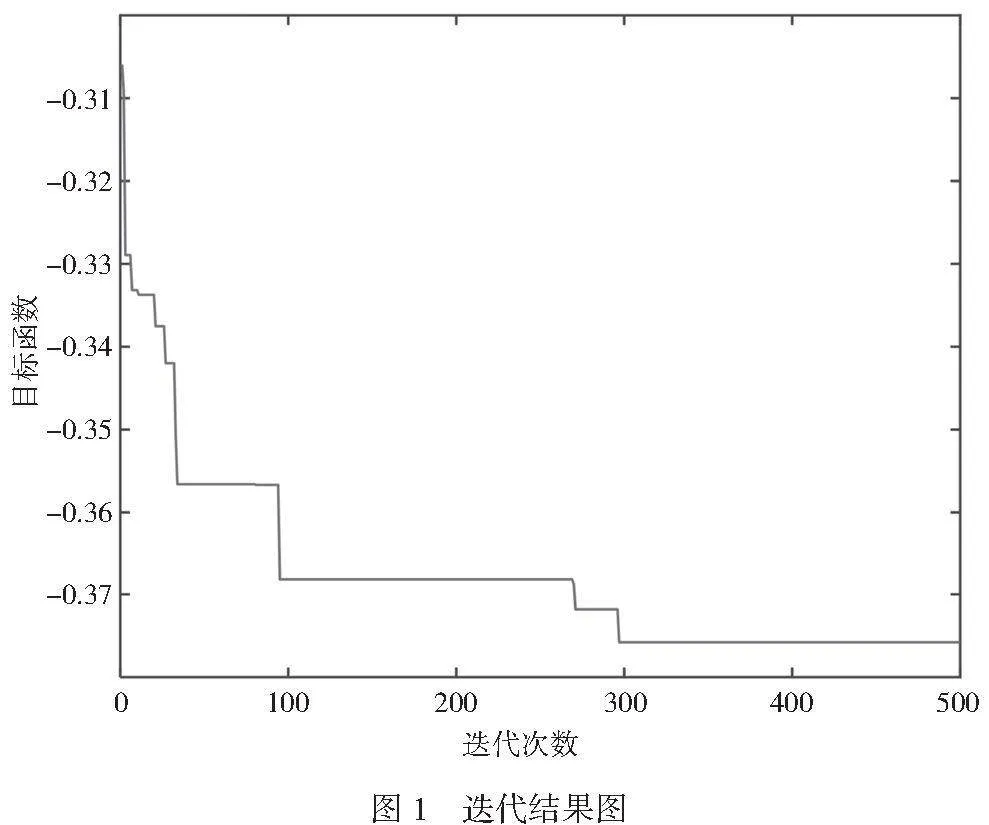
根据专家打分设置上述算例中的目标函数的权重，其中f1=0.5，f2=0.5。将和声记忆库的大小HMS设置为100，音调微调概率PAR设置为0.2，和声记忆库的取值概率HMCR设置为0.96，迭代次数Tmax设置为500，遗传算法中交叉概率Pc设置为0.95，变异概率Pm设置为0.1。利用MATLAB进行500次迭代，所得迭代结果曲线和布局结果分别如图1和图2所示。

过进一步对初始布局和改进后布局的目标函数进行计算，结果见表2。结果表明，新布局的运输成本比原布局降低了24.2%，非物流关系提升了23.7%。

4 Flexsim仿真

虽然使用SLP方法和改进和声算法改进了A车间布局，使运输成本和非物流关系达到最优，但是生产系统是一个复杂的动态随机系统[8]，仅靠算法求解的结果很难体现各要素间的相互作用，因此本文采用Flexsim仿真，建立A公司车间布局仿真模型并输出仿真报告，进一步验证改进的有效性。

分别将改进布局和原始布局的布局图分别按照1∶1的比例代入Flexsim中，在搭建模型的过程中，选择相应的实体并设置相应的动态参数。

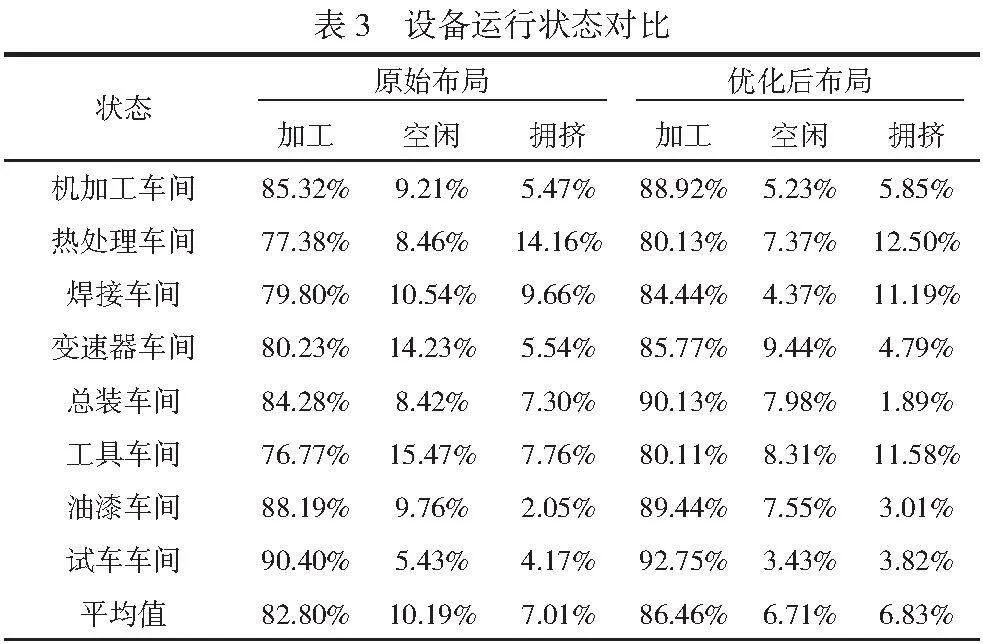
为判断改进后的布局是否合理改进，本文将设备工作状态作为观测结果，生成各个车间设备的工作状态，见表3。比较原始布局和优化后的布局可知，原始布局的设备平均加工时间约为82.80%，平均空闲时间约为10.19%，平均拥挤时间约为7.01%，优化后布局的设备平均加工时间为86.46%，比原始布局提升3.66%，平空闲时间约为6.71%，比原布局降低3.84%，平均拥挤时间约为6.83%，比原布局降低了0.18%。可见从设备运行状态来看，改进后的布局比原始布局效果更好。

5 结论

本文针对车间布局问题建立模型，设置运输成本最小化和非物流关系最大化2个目标函数，采用改进和声算法对A车间进行优化布局，得到最优布局方案，最后利用仿真软件Flexsim验证布局的可靠性。结果表明，改进和声算法在车间布局中取得了良好效果。

参考文献

[1]姚明钊，陈鹏飞，裴小兵.基于SLP和改进遗传算法优化C企业车间布局[J].有色金属工程，2023，13（9）：99-109.

[2]邓兵，林光春.改进SLP和遗传算法结合的车间设备布局优化[J].组合机床与自动化加工技术，2017（8）：148-151，156.

[3]丁祥海，韦新立，姚文鹏.考虑柔性面积需求的动态设施布局方法研究[J].工业工程与管理，2018，23（5）：116-125.

[4]郑广辉，钱叶昶，刘鹏，等.基于遗传和声算法的复兴号部件生产车间布局研究[J].机床与液压，2023，51（4）：57-62，66.

[5]张青雷，党文君，段建国.基于自适应遗传算法的大型关重件车间布局优化[J].机械设计与制造，2021（1）：236-239.

[6]张思奇，于登辉，郑一明，等.基于多目标候鸟算法的车间布局研究[J].现代制造工程，2022（2）：16-23.

[7]王俊杰，蔡芸，熊禾根.基于遗传算法的双层车间设施布局优化研究[J].物流科技，2023，46（11）：53-56.

[8]邢彩虹，刘刚，胡晓兵，等.基于SLP改进遗传算法的多区域单双行设备布局优化方法[J].四川大学学报（自然科学版），2022，59（5）：70-78.