箱型桥梁截面参数对风致行车安全的影响研究

摘 要：双幅箱型桥梁的宽高比和间距是影响桥面风场及桥上车辆气动性能的关键设计参数，为提高强风载荷下桥梁的风致行车安全能力，本文以双向六车道双幅桥为研究对象，采用计算流体动力学方法建立了不同截面参数组合下的气动分析模型，获取了不同车道的桥面风场参数及车辆气动性能。结果表明，较小的宽高比和桥梁间距对桥面风场的干扰更小，不同车道的等效风速更低，更利于保障车辆的行驶安全。

关键词：截面参数；桥梁间距；桥梁宽高比；典型车辆；风致行车安全

中图分类号：U 44" " 文献标志码：A

跨海桥梁是连接城市交通节点的重要枢纽，在带来便捷交通的同时，强风气候下也容易诱发风致行车安全事故。“桥梁与桥梁”、“汽车与桥梁”、“桥梁与侧风”之间的相互气动影响不容轻视[1-2]，当车辆在跨海大桥上行驶时，强侧风会导致车辆的行驶稳定性发生变化[3]，致使车辆发生侧滑、侧翻等危险情况，因此，本文以《桥梁挡风障关键参数及行车安全性研究》科研项目为研究背景，开展跨海桥梁的截面参数对风致行车安全研究具有重要的工程意义。

侧风、桥梁与汽车的交互气动干扰与众多因素有关，其中，桥梁截面参数的影响尤为重要，例如桥梁宽高比、桥梁间距和桥面附属构造等[4-7]。本文以双向六车道双幅桥（参数来源于《桥梁挡风障关键参数及行车安全性研究》项目实体模型）为研究对象，采用计算流体动力学方法建立不同截面参数组合下的气动分析模型，获取不同车道的桥面风场参数及车辆气动参数，研究结果可以为指导跨海桥梁的截面设计提供参考。

1 桥面风环境数值模拟

1.1 计算模型

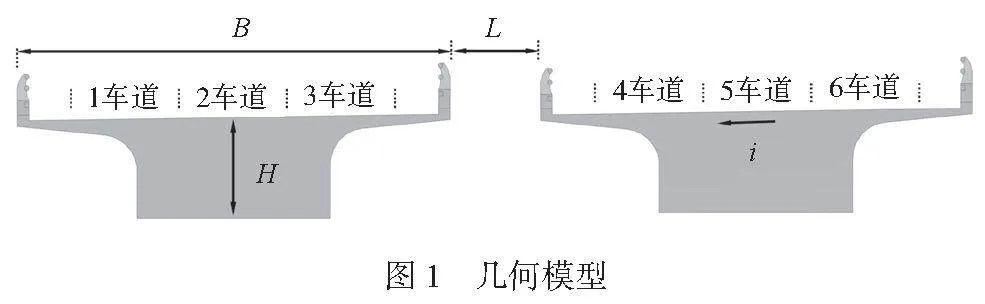
为研究双向六车道双幅桥的截面和间距对车辆行车的影响，取3种宽高比（2.5、3.5和4.5）、3种桥梁间距（2.5m、5.0m和10.0m）进行研究。图1为某桥梁截面与间距的桥梁模型，图1中所标注的为桥梁基本参数代号，横坡为i=1.5，单幅桥宽为B=12m，车道宽为3.5m。本文共建立了9种不同的双幅箱梁桥梁工况，不同工况采用“B/H-L”进行命名，其中B/H代表变截面桥梁不同截面的宽高比，L为桥梁间距。

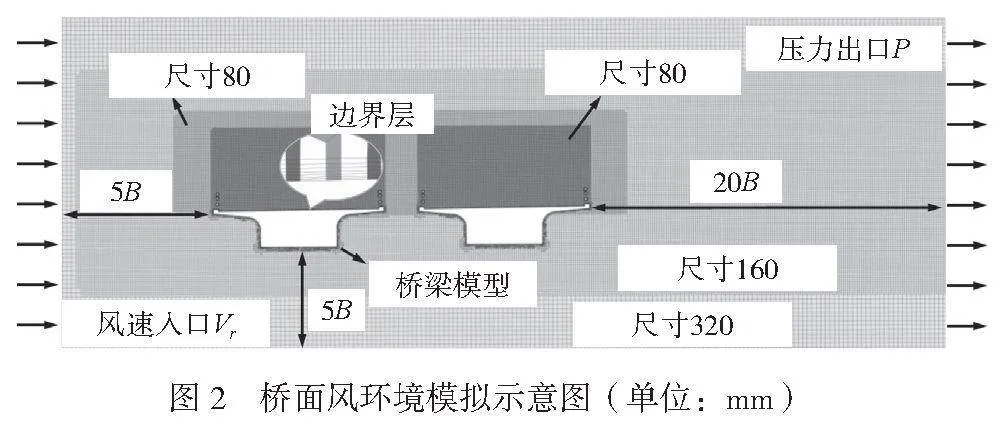
当计算桥面风场时，为减小边界条件对监测点的影响，当对不同桥梁模型桥面风场进行模拟时，桥梁长度统一取50m，并参考公路桥梁抗风设计规范[8]中虚拟风洞的尺寸搭建桥面风场模拟所需的流体域。经过网格无关性验证分析，在兼顾计算效率和精度的前提下确定以下网格设置方案：体网格采用Fluent Meshing中的六面体网格，桥梁栏杆面网格为20mm，其他位置面网格为128mm，最大六面体网格为640mm；为了更准确模拟监测区域的桥面风场，对该区域进行局部加密，其加密尺寸为320mm、160mm、80mm和40mm，为捕捉近壁面的风速变化，在桥梁不同面上添加7层边界层网格，第一层边界层网格的高度为0.94mm，边界层网格的增长速率为1.2，最后桥面风场计算域中的体网格总量达到6600万左右，桥面风环境计算示意如图2所示。

采用SSTk-omega湍流模型、SIMPLE算法以及二阶迎风离散格式求解。本文设置侧风环境速度Vr为20.8m/s，不同车道的风速检测点均在桥梁中心面上，且监测点位于车道中心线正上方。为检测集装箱货车高度的风速，本文的风速监测高度为4.5m，每隔0.25m设置1个监测点，每一车道共18个监测点，双幅桥梁上风速监测点共108个。

1.2 桥面风环境评估参数

采用等效风速和风速折减系数评估桥面风场。当风作用于桥梁时，风速会随着离桥面高度的不同而变化，为了衡量桥面在某一高度范围内风速效应，采用等效风速[9]的概念，等效风速基于风压剖面等效的原则定义，如公式（1）所示。

式中：Zr为等效高度，轿车的等效高度取值Zr=2.0m，集装箱货车等效高度取值为Zr=4.5m；V为桥面不同高度的风速；z为离桥面高度。

为了评估桥梁的宽高比及其间距对来流风场的影响，本文将等效风速无量纲化为风速折减系数，该系数为等效风速与参考风速之间的比值，用β表示。用风速折减系数以衡量不同桥梁设计参数对风场干扰作用的程度，如公式（2）所示。

式中：Vr为参考风速（入口风速）。

1.3 风洞试验验证

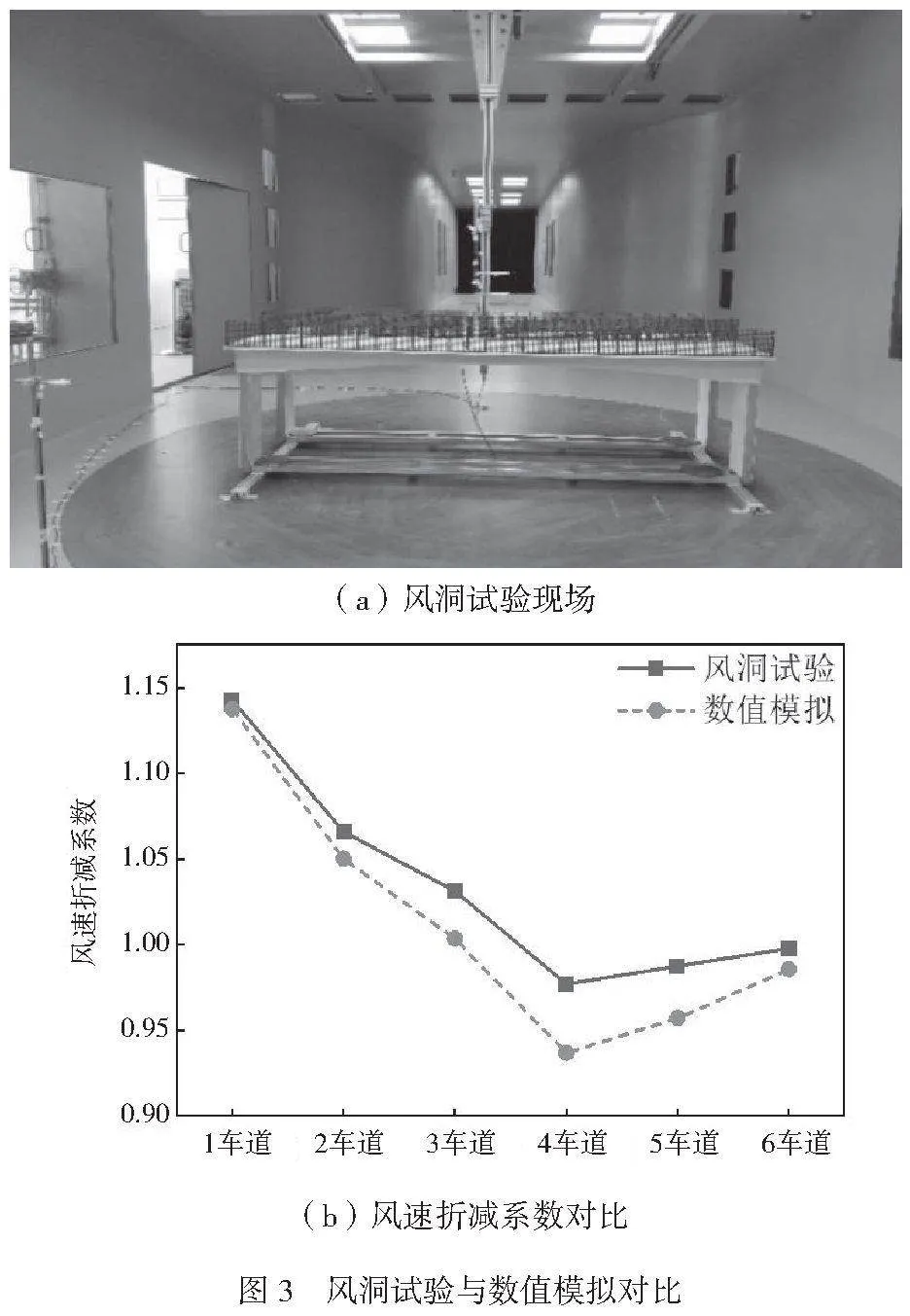
根据上述桥面风场网格尺寸设置建立与风洞试验对应的桥面风场计算模型，保证计算模型桥梁和风洞试验桥梁模型一致，风洞试验中桥梁模型比例为1∶20，入口风速为10m/s，数值模拟中湍流模型以及边界条件与上述保持一致。在本次验证中，监测范围为5m，检测点的设置与上述设置方法一样并同风洞试验的监测位置一致，最后利用等效风速与风速折减系数的公式算出风洞试验与模拟仿真不同车道的风速折减系数，如图3所示。

风洞试验所得到的第1车道～6车道风速折减系数分别为1.1426、1.0659、1.0312、0.9771、0.9875、0.9978，数值模拟数据为1.1373、1.0500、1.0034、0.9367、0.9571、0.9858，两者较接近，表明本文的数值计算模型较准确。

2 桥面风场分析与讨论

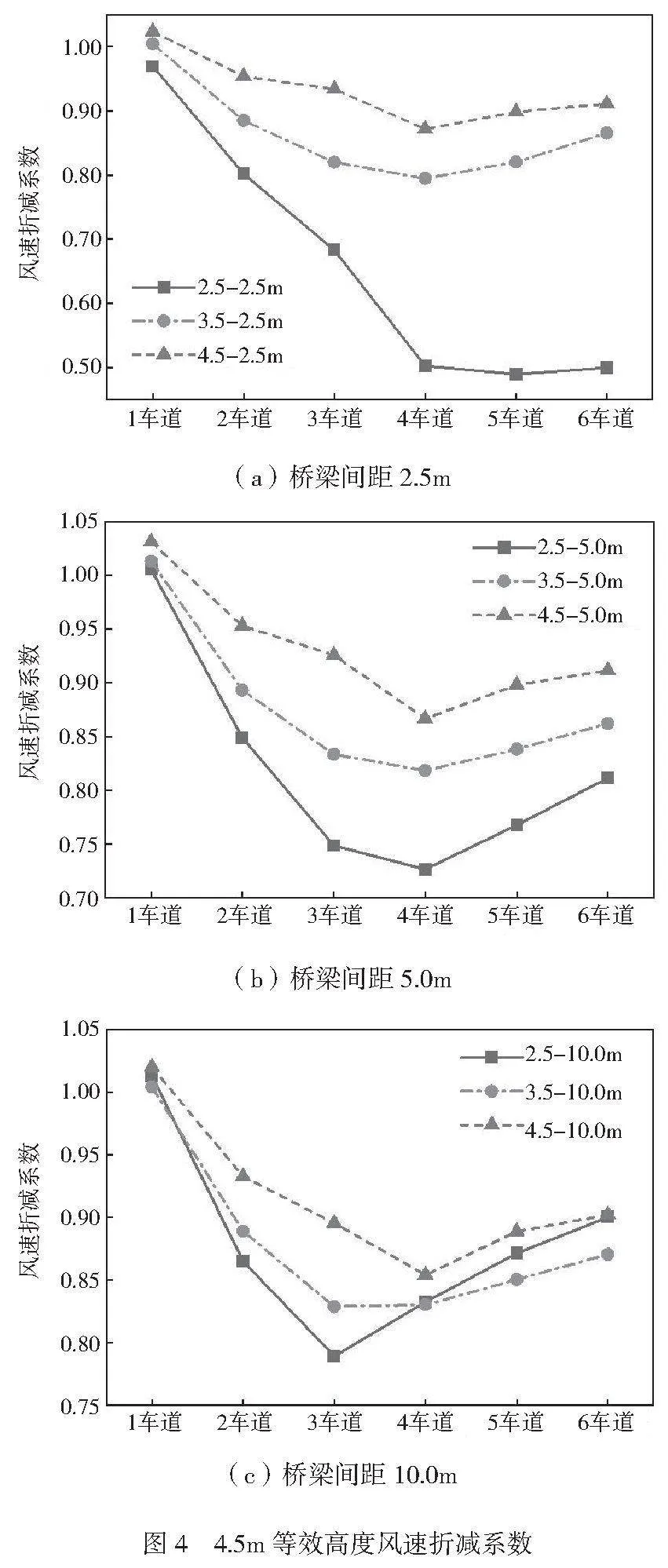
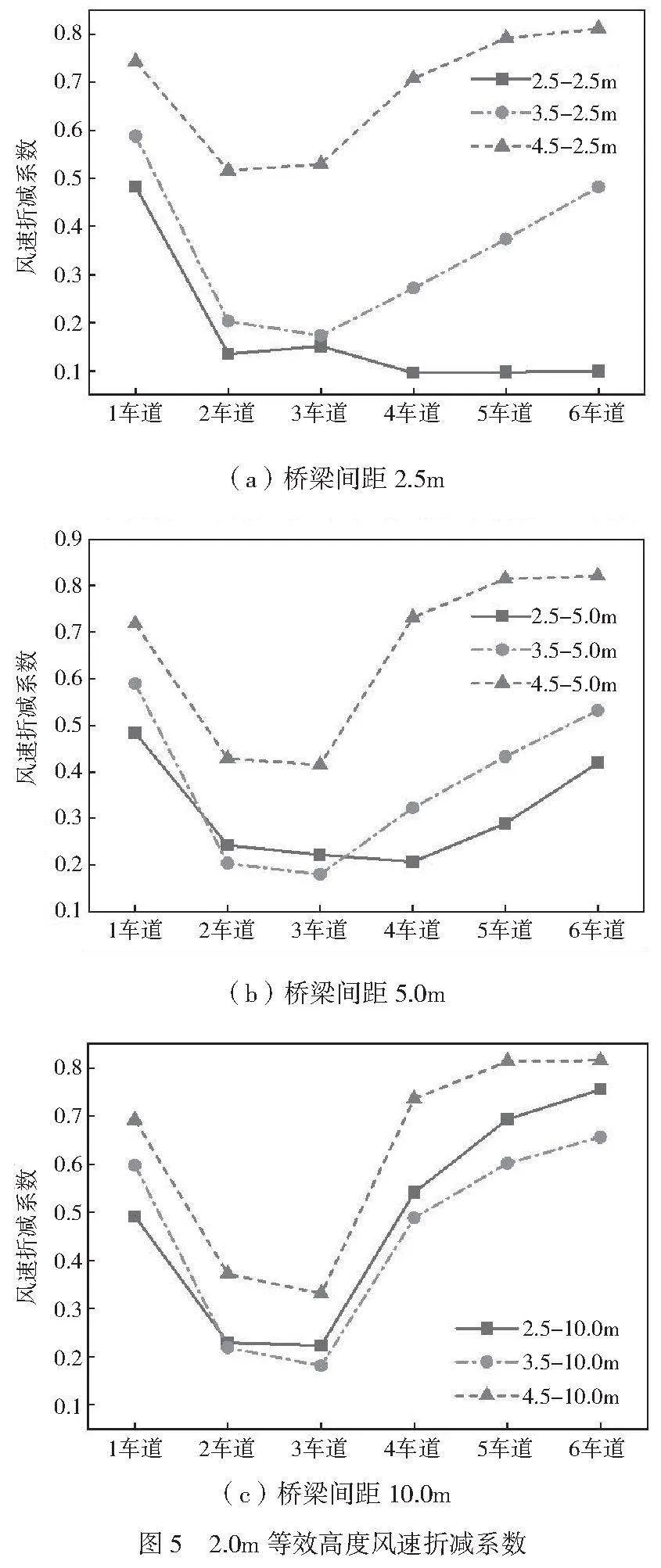
不同桥梁高宽比、不同等效高度以及不同车道下的桥面风场如图4、图5所示，桥梁宽高比是影响桥面风场的主要参数。

不同工况下，迎风侧桥的第一车道至第三车道风速折减系数逐渐降低，而背风侧桥梁第四车道至第六车道的风速折减系数逐渐增加。与迎风侧的桥梁相比，背风侧的桥梁受到的影响更大，而且，随着桥梁宽高比增加，桥梁间距对桥面风速折减系数的影响逐步降低。

当等效高度为4.5m时，对迎风侧桥梁车道来说，宽高比越小，各车道的风速折减系数越小，对远离迎风侧的车道三影响最大，而对接近迎风侧的车道一影响最小；对背风侧桥梁车道来说，当桥梁间距较小时，宽高比越小，各车道的风速折减系数越小，当桥梁间距较大（10m）时，随着宽高比减小，各车道的风速折减系数先变小后变大。

当等效高度为2m时，对迎风侧桥梁车道来说，当桥梁间距较小（2.5m）时，宽高比越小，各车道的风速折减系数越小，而当桥梁间距较大时，随着宽高比变小，车道一的风速折减系数越小，而远离迎风侧的车道二和车道三的风速折减系数先变小后变大。对背风侧桥梁来说，当桥梁间距较小时，宽高比越小，各车道的风速折减系数越小，当桥梁间距较大（10m）时，随着宽高比小，各车道的风速折减系数先变小后变大。

不同桥梁截面参数下的桥面风场如图6所示。当桥梁间距较小时，宽高比的变化对桥面风场有较大的影响，特别是对背风侧桥梁。当桥梁宽高比较小时，桥梁间距的变化对桥面风场有较大的影响，特别是对背风侧桥梁。

3 桥上车辆气动分析与讨论

3.1 数值计算模型

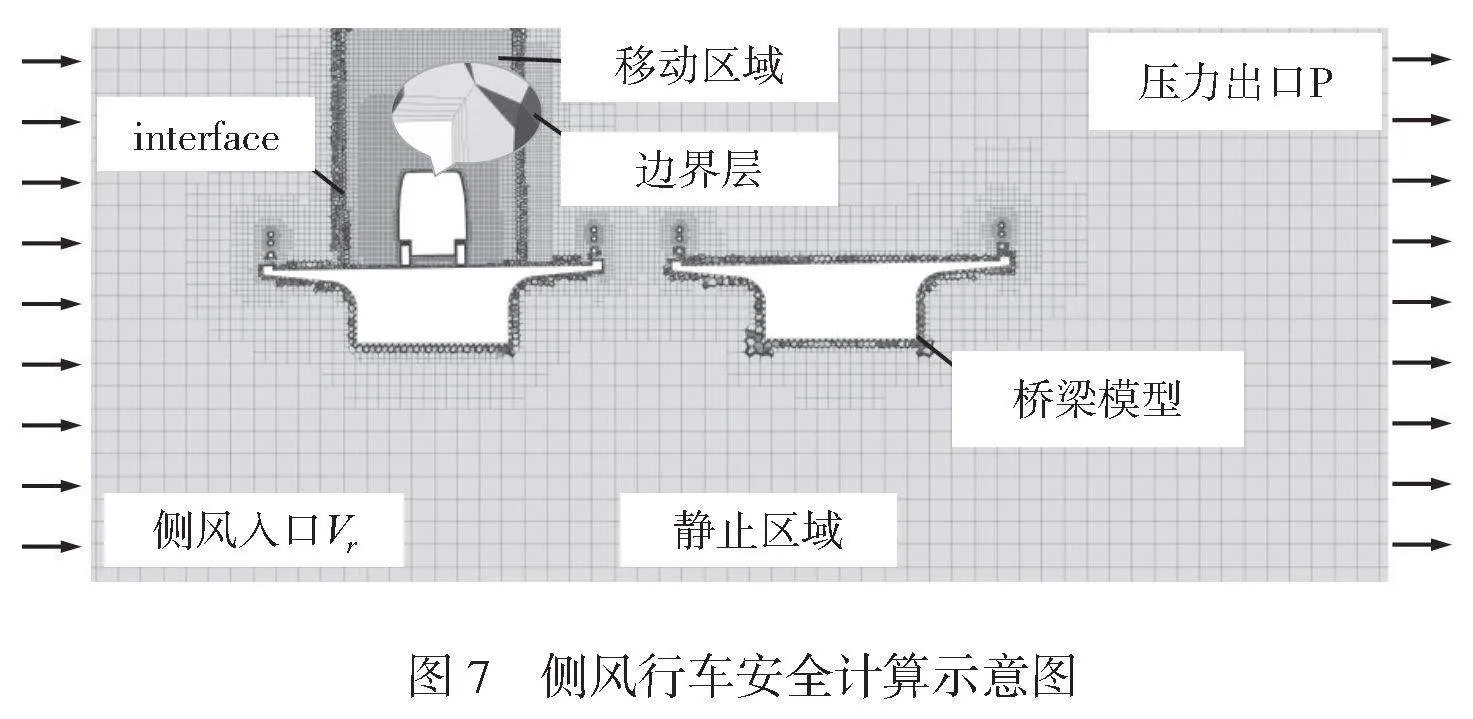
桥上车辆行车的气动分析计算示意如图7所示，采用滑移网格方法建立计算模型，其中，集装箱货车长宽高尺寸分别为14.92.43.9m，车速为80km/h，轿车长宽高尺寸分别为5.050m2.11.5m，车速为100km/h。

采用Fluent Meshing中的Ploy-Hexcore进行网格划分，静止区域的网格设置为400mm，移动区域的最大网格尺寸为320mm，为更准确模拟车辆周围的流场，对车辆周围进行加密，加密尺寸为160mm和80mm，并对车辆共设置4层边界层，第一层高度1mm，增长率为1.1，静止区域和移动区域的体网格总和为4200万左右。本文设置侧风环境速度Vr为20.8m/s，采用realizable k-e湍流模型、SIMPLE算法以及二阶迎风离散格式进行求解计算。

3.2 集装箱货车桥上行车气动分析

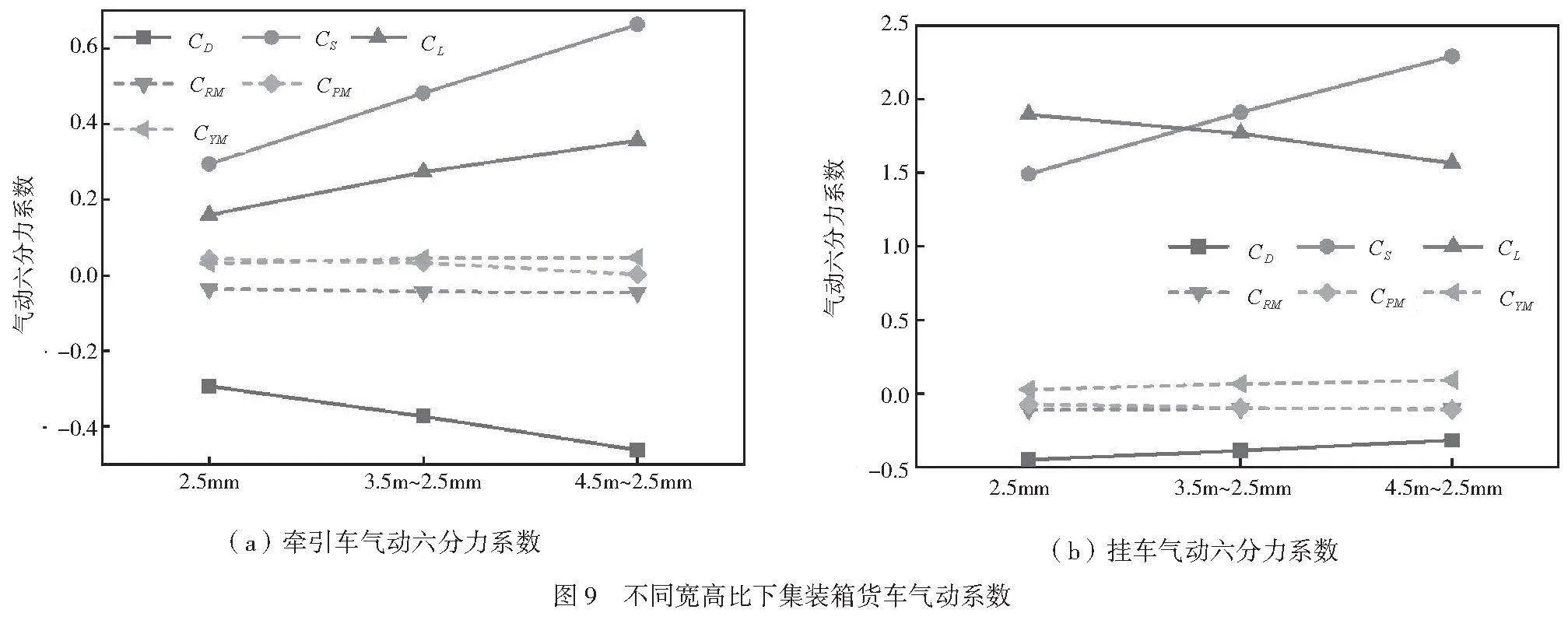
桥梁间距为2.5m，不同宽高比工况下牵引车前轴YZ截面的速度云图如图8所示，汽车行驶在迎风侧桥梁的第二车道上，桥面风环境的差异导致集装箱货车的气动六分力存在较大的差异，具体变化如图9所示。

由图8可知，宽高比的变化对集装箱货车迎风侧车道和背风侧桥梁车道的流场有较大的影响，宽高比越大，栏杆对迎风侧桥面的有效遮挡高度越小，对车辆迎风侧的气流影响越明显，但迎风侧桥梁的尾流对背风侧桥面的风场影响越小。

在气动六分力中，气动侧力和气动横摆力矩是影响汽车风致行车安全的主要因素，桥梁宽高比逐渐增大，牵引车的气动侧力和气动横摆力矩均发生不同程度的增幅，其中，气动侧力的变化幅度更高。与桥梁宽高比为2.5工况相比，随着桥梁宽高比增大，牵引车的气动侧力系数分别增长0.1880、0.3689，挂车的气动侧力系数分别增长0.4183、0.8017；牵引车的气动横摆力矩系数分别增长0.0132、0.0164，挂车的气动横摆力矩系数分别增长0.0387、0.0640。

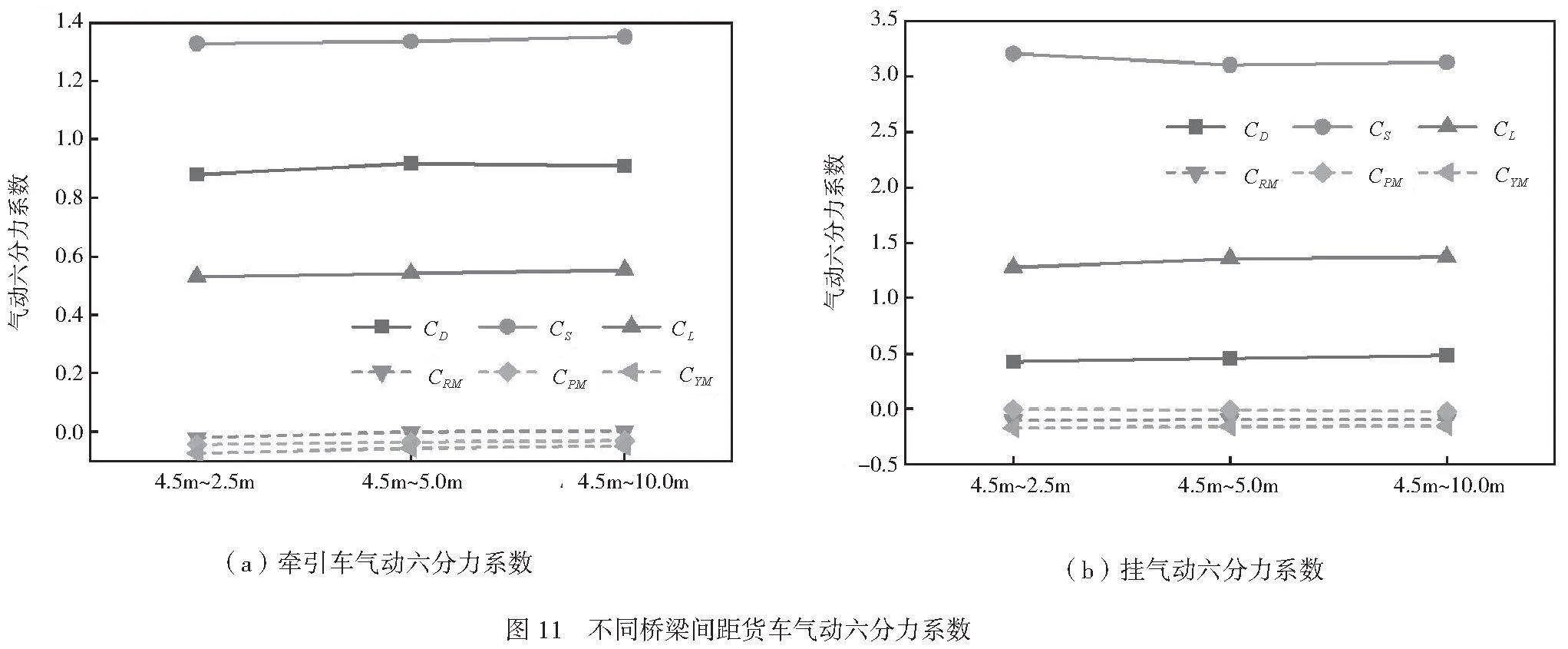
桥梁宽高比为4.5m，不同桥梁间距工况下牵引车前轴YZ截面的速度云图如图10所示，汽车行驶在背风侧桥梁的第五车道上。当桥梁宽高比较小时，桥梁间距的变化对背风侧桥面风场影响较大，当桥梁宽高比较大时，对背风侧桥面风场的影响较小。因此，该工况下桥梁间距对集装箱货车气动特性影响不大，如图11所示。与桥梁间距为2.5m工况相比，随着桥梁间距增大，牵引车的气动侧力系数分别增长0.0077、0.0221，挂车的气动侧力系数分别减小0.1029、0.0791；牵引车的气动横摆力矩系数分别减小0.0167、0.0237，挂车的气动横摆力矩系数分别减小0.0131、0.0142。

3.3 轿车桥上行车气动分析

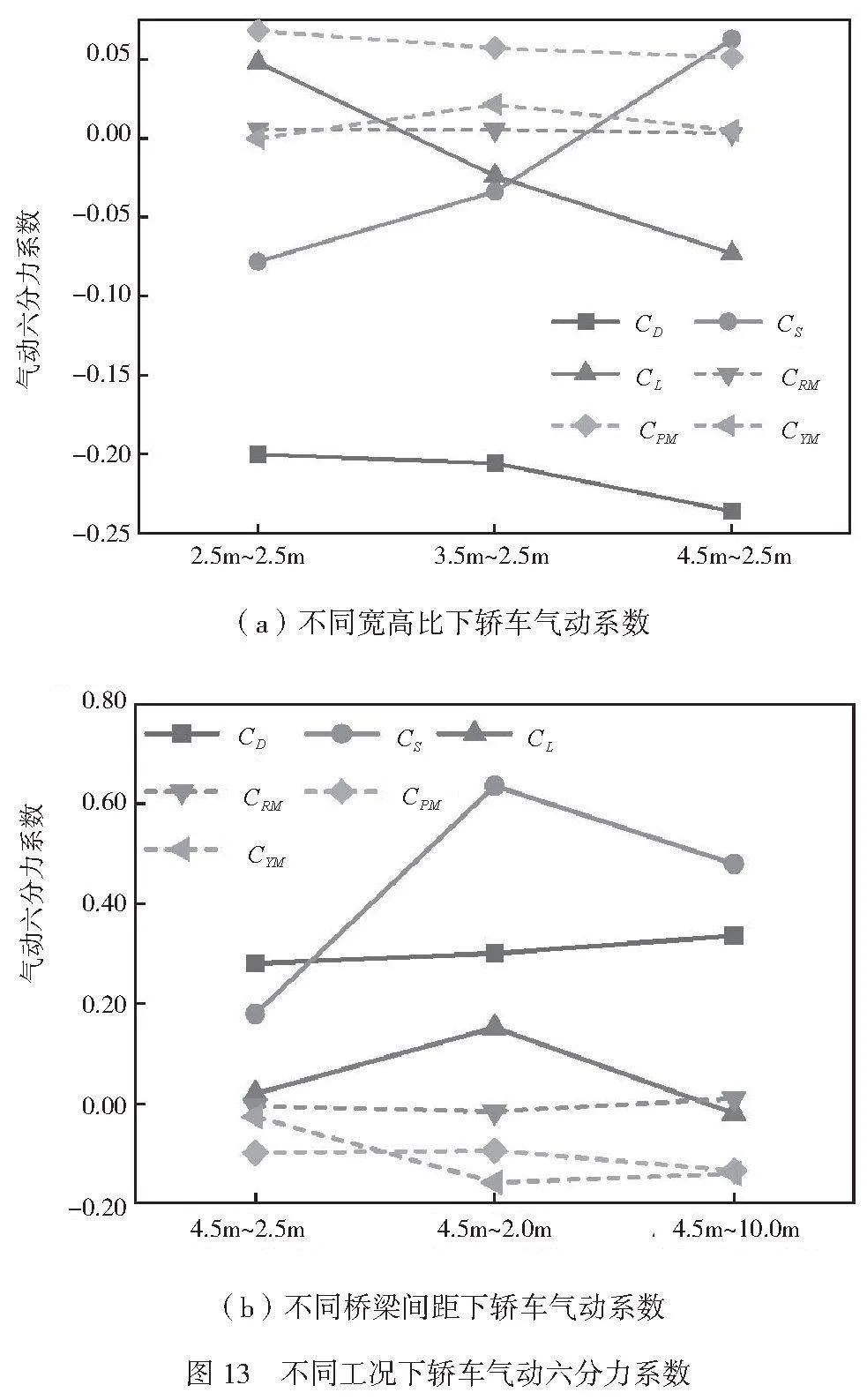
不同宽高比和间距工况下轿车前轴YZ截面的速度云图如图12所示，汽车行驶在迎风侧桥梁的第二车道和背风侧桥梁第五车道上。不同工况下的轿车周围流场存在明显差异，随着宽高比增大，栏杆的扰流作用产生的加速区越来越低，轿车上方的流速越来越大。当桥梁间距较小时，由于迎风侧桥梁的阻风效果，轿车直接处于低速尾流区，当桥梁间距较大时，车辆迎风侧的风速会有一定程度增大。不同工况下的轿车气动系数如图13所示。

由图13（a）可知，当桥梁间距为2.5m时，随着桥梁宽高比变小，轿车的侧向力先变小再变大，由推力逐渐变成吸力，而气动横摆力矩则先增加后减小，该工况下，气动侧力和气动横摆力矩均不大，对行驶稳定性的影响较小。由图13（b）可知，当桥梁宽高比为4.5时，随着桥梁间距缩短，轿车的侧向力和横摆力矩先变大后变小。与桥梁间距为2.5m工况相比，随着桥梁间距缩短，轿车的气动侧力系数分别增长0.4571、0.3005，轿车的气动横摆力矩系数分别增长0.1322、0.1141。

4 结语

综上所述，本文得出以下结论。1）随着桥梁宽高比减小，各车道的风速折减系数逐渐变小，集装箱货车和轿车所受的气动干扰变小，汽车的行驶稳定性更好。2）当桥梁宽高比较小时，桥梁间距的变化主要影响背风侧桥梁桥面风场，间距越小，风速折减系数越小，集装箱货车和轿车的行驶稳定性更好。3）当桥梁宽高比较大时，桥梁间距的变化主要影响迎风侧桥梁桥面风场，间距越大，风速折减系数越小，集装箱货车和轿车的行驶稳定性更好。4）为提高桥上车辆的风致行车安全能力，可以考虑在桥幅两侧增设桥梁挡风障，保障强风或者台风气候下的桥上车辆行驶稳定性。

参考文献

[1]刘小兵，姜会民，刘慧杰，等.不同宽高比并列双幅箱梁气动升力的干扰效应[J].振动、测试与诊断，2023，43（1）：103-108.

[2]袁志群，刘宇峰，林立.强风环境下跨海桥梁行车安全评价与管控方法[J].汽车工程，2022，44（9）：1456-1467.

[3]袁志群，吕恒庆，林立，等.跨海大桥上厢式货车侧风稳定性的研究[J].汽车工程，2021，43（8）：1-6.

[4]韩艳，陈浩，胡朋，等.基于CFD的流线型桥梁断面阻力系数测压结果修正研究[J].铁路科学与工程学报，2016，13（1）：97-102.

[5]刘小兵，杨少杰，杨群，等.并列双箱梁的气动干扰效应对阻力系数的影响[J].中国公路学报，2017，30（11）：109-114.

[6]夏锦林，李珂，葛耀君，等.不同风障形势下桥梁断面行车风环境及颤振性能[J].哈尔滨工业大学学报，2017，49（3）：98-105.

[7]袁达平，郑史雄，洪成晶，等.大跨公铁两用斜拉桥塔区风环境[J].哈尔滨工业大学学报，2018，50（9）：20-24.

[8]同济大学.公路桥梁抗风设计规范：JTG/T3360-01-2018[S].北京：中华人民共和国交通运输部，2019：171.

[9]吴凤英，赵林，曹丰产，等.开槽箱梁设置风障行车风环境模拟、试验与实测[J].哈尔滨工业大学学报，2022，54（3）：21.