软岩高边坡稳定性及影响因素数值模拟研究

摘 要：为研究软岩高边坡的稳定性及影响因素，本文以某软岩高边坡为研究对象，基于ABAQUS有限元软件，分析边坡土体黏聚力、内摩擦角、坡度及弹性模量等对边坡稳定性的影响。研究结果表明，黏聚力对边坡稳定性的增大效果随黏聚力的增大先增大后趋于稳定；内摩擦角对边坡稳定性的增大效果随内摩擦角的增大先增大后减小；坡度对边坡稳定性的减小效果随坡度的增大逐渐降低；增大黏聚力，增大内摩擦角，减小坡度，边坡的安全系数越大，且弹性模量对边坡安全系数的影响远小于其他3个因素。

关键词：软岩高边坡；数值模拟；稳定性；影响因素

中图分类号：" U 416 文献标志码：A

目前，国内外学者分别从不同角度对软岩高边坡稳定性进行了一系列研究，刘新喜等[1]建立了饱和与非饱和渗流有限元模型，研究了不同降雨强度、持时和压实度等条件下边坡稳定性的变化规律；李海洲等[2]基于FLAC3D有限元软件，结合室内单轴压缩蠕变试验数据，研究了砂质泥岩弱层强度参数对边坡稳定性的影响；何忠明等[3]基于FLAC3D有限元软件，分析了软岩高边坡开挖施工过程中变形、安全系数的变化规律；蒋中明等[4]基于渗流场的分布特点及变化规律对FLAC3D单元强度时间效应和重度变化的空间分布特性进行了修改，研究了软化-渗流耦合作用下软岩高边坡的稳定性变化；姚文敏等[5]基于FLAC3D强度折减法，研究了岩层倾角、岩层与边坡走向夹角对边坡稳定性的影响，并归纳了软硬互层边坡的破坏模式。综上所述，软岩高边坡极易出现滑坡现象，不同土体边坡稳定性差异也十分明显，因此研究不同土体边坡稳定性对不同因素的敏感性尤为重要；基于ABAQUS强度折减法，针对西南软岩高边坡稳定性影响因素的研究较少。

鉴于此，本文以某软岩高边坡为研究对象，基于ABAQUS有限元软件，分析边坡土体黏聚力、内摩擦角、坡度及弹性模量等对边坡稳定性的影响，为边坡安全评价及加固提供科学依据。

1 工程概况

本文以某软岩高边坡为研究对象，该区域为亚热带半湿润气候区，平均温度常年为11℃～18℃，年日照时间为2000h～2600h，年降水量900mm～1200mm，降雨集中在5—10月。区域范围内地形起伏较大，存在众多高边坡，对坡下居民生命安全造成极大的安全隐患。

2 数值模型的建立

本文通过强度折减法计算边坡稳定系数，ABAQUS通过控制材料参数变化来模拟岩土体黏聚力、内摩擦角的折减，一般认为模型位移突变时刻模型失稳，发生破坏。将材料参数变化与模型位移数据导入软件自带的combine函数，从而得到模型的安全系数。

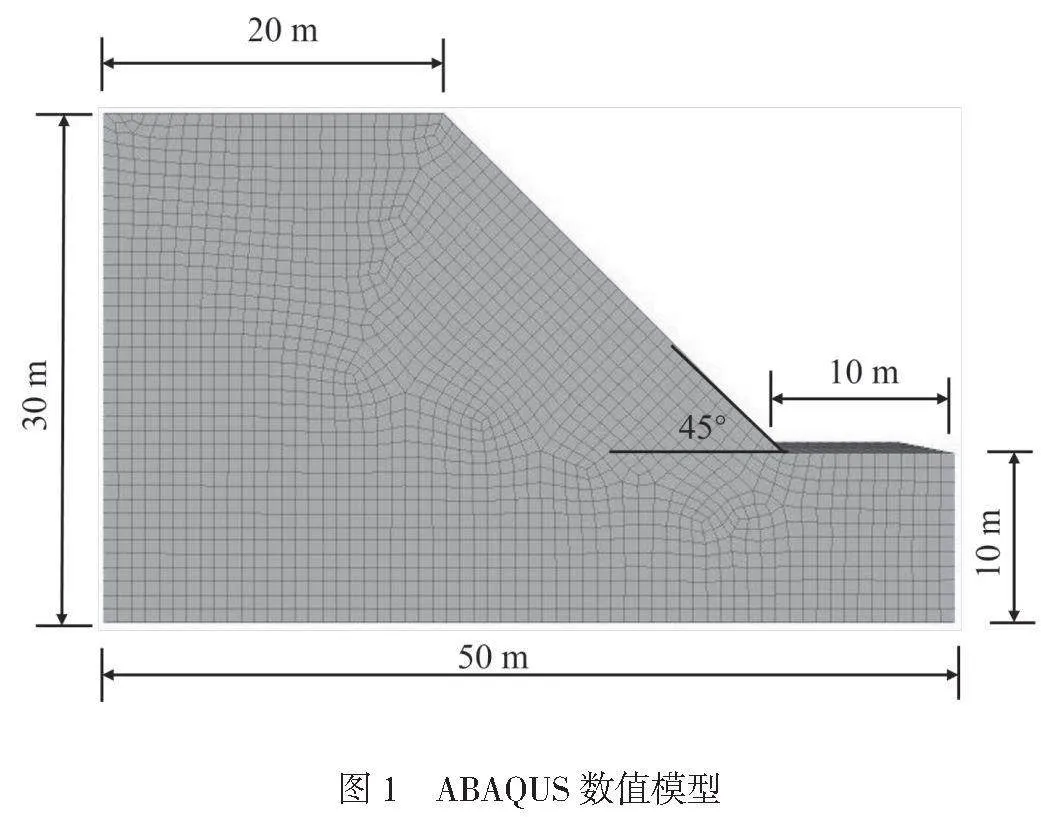
本文以某软岩高边坡为研究对象，基于ABAQUS有限元软件，建立边坡数值模型，如图1所示。

由图1可知，边坡高为30m，底面长为50m，顶面长为20m，坡脚高为10m，坡度为45°，模型结构具体物理力学参数见表1。

该边坡主要由泥岩组成，通过查阅资料，将边坡初始弹性模量设置为350MPa，泊松比设置为0.25，容重设置为25kN/m3，黏聚力设置为40kPa，内摩擦角设置为25°。

3 结果分析

现有研究表明边坡土体的黏聚力、内摩擦角、坡度及弹性模量均会对边坡稳定性产生影响，因此本文研究不同黏聚力、内摩擦角、坡度及弹性模量条件下泥岩边坡安全系数的变化规律。

3.1 黏聚力对边坡稳定的影响

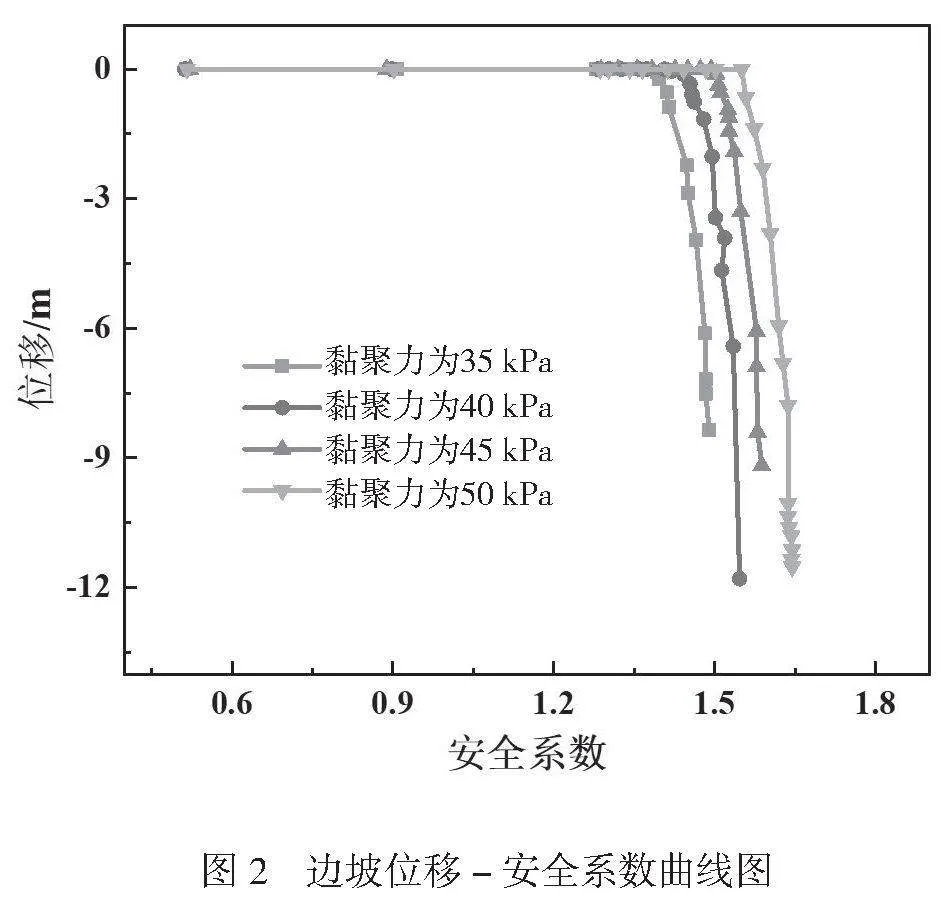
为研究不同黏聚力条件下边坡稳定性的变化规律，设置4种黏聚力梯度：35kPa、40kPa、45kPa、50kPa。通过计算得到模型黏聚力折减过程中边坡的位移，最后通过combine函数计算该折减系数下的边坡安全系数。不同黏聚力条件下边坡位移-安全系数曲线如图2所示。

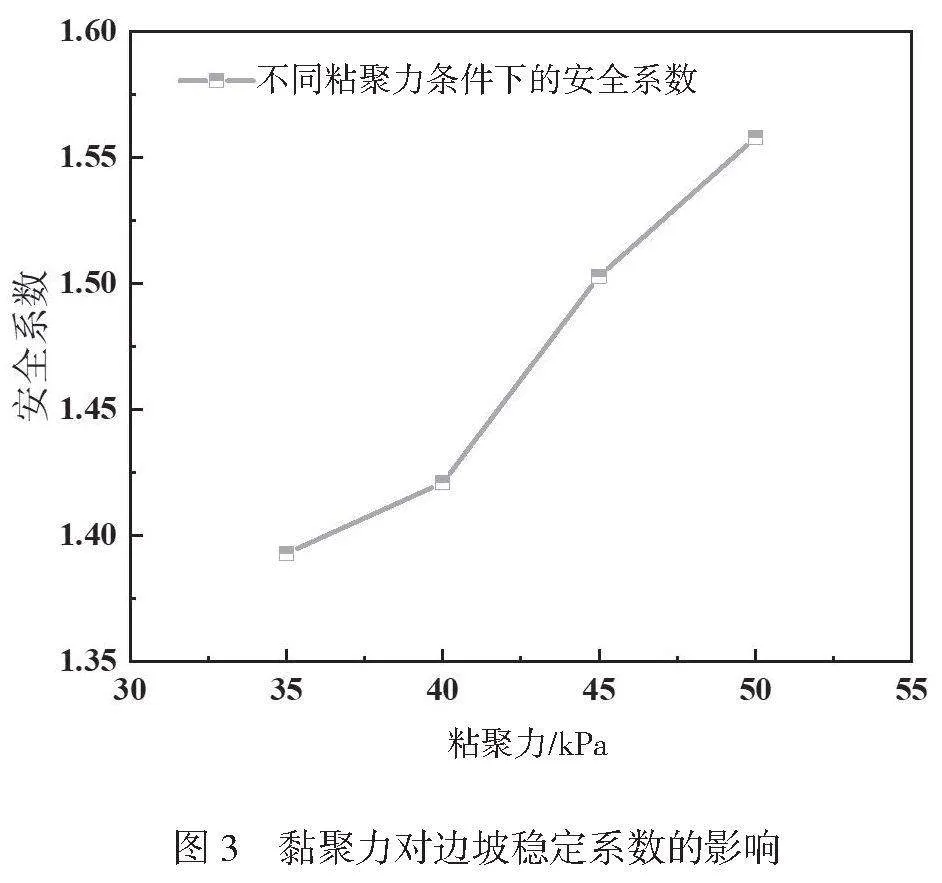
由图2可知，在强度折减过程中，随着折减系数增大，边坡安全系数逐渐增大，边坡位移先保持稳定后发生位移突增现象。4种黏聚力在强度折减过程中发生位移突变点不同，将位移突变点横坐标作为该黏聚力条件下边坡安全系数。不同黏聚力对应的边坡安全系数如图3所示。

由图3可知，边坡安全系数随黏聚力增大逐渐增大，黏聚力35kPa、40kPa、45kPa、50kPa对应的边坡安全系数分别为1.393、1.421、1.503、1.558。与粘聚力为35kPa相比，边坡安全系数增量分别为0.031、0.11、0.165，分别增大了2.23%、7.9%、11.84%。增大黏聚力对边坡安全系数的增大效果分别为2.23%/5kPa（40kPa）、3.95%/5kPa（45kPa）、3.95%/5kPa（50kPa），说明黏聚力对边坡安全系数的增大效果随黏聚力的增大先增大后趋于稳定。

3.2 内摩擦角对边坡稳定的影响

为研究不同内摩擦角条件下边坡稳定性的变化规律，设置4种内摩擦角梯度：20°、25°、30°、35°。得到不同内摩擦角条件下边坡位移-安全系数曲线如图4所示。

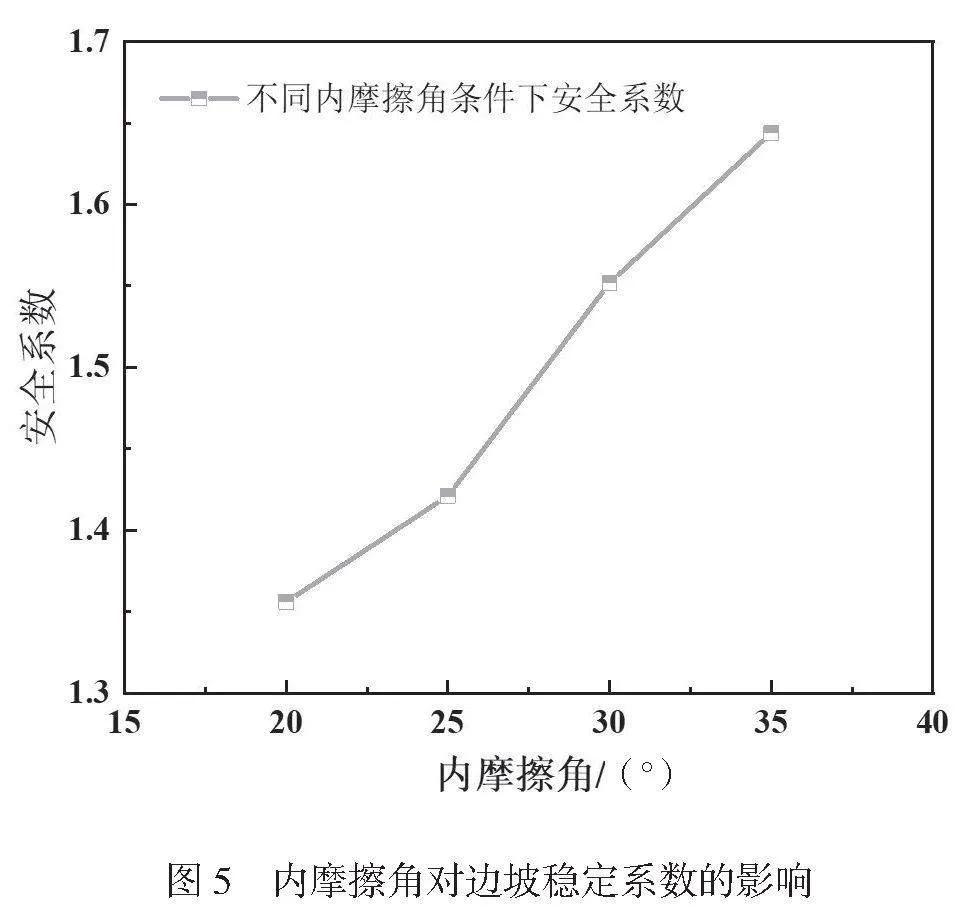
由图4可知，4种内摩擦角在强度折减过程中发生位移突变点不同，将位移突变点横坐标作为该内摩擦角条件下边坡安全系数。不同内摩擦角对应的边坡安全系数如图5所示。

由图5可知，边坡安全系数随内摩擦角的增大逐渐增大，内摩擦角为20°、25°、30°、35°对应的边坡安全系数分别为1.356、1.421、1.552、1.644。与内摩擦角为20°相比，边坡安全系数增量分别为0.065、0.196、0.288，分别增大了4.79%、14.45%、21.24%。内摩擦角对边坡安全系数的增大效果分别为4.79%/5°（25°）、7.23%/5°（30°）、7.08%/5kPa（35°），说明内摩擦角对边坡安全系数的增大效果随内摩擦角的增大先增大后减小。

3.3 坡度对边坡稳定的影响

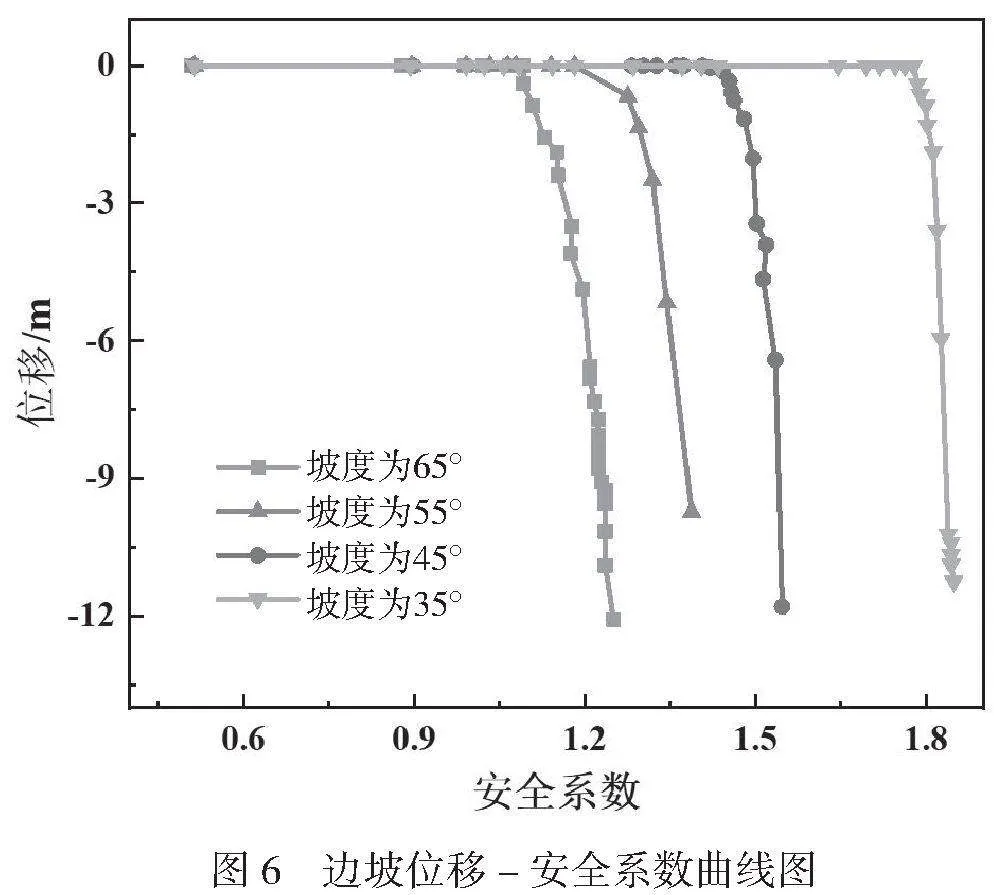
为研究不同坡度条件下边坡稳定性的变化规律，设置4种坡度梯度：35°、45°、55°、65°。得到不同坡度条件下边坡位移-安全系数曲线如图6所示。

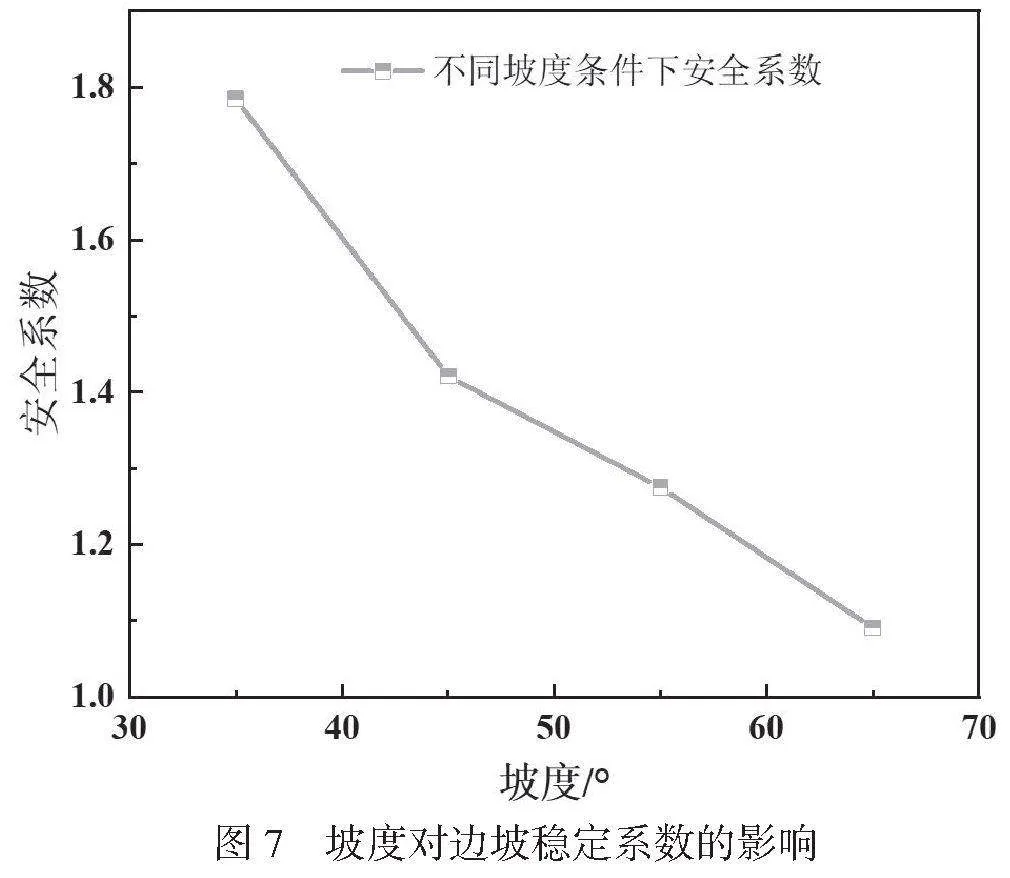
由图6可知，4种坡度在强度折减过程中发生位移突变点不同，将位移突变点横坐标作为该坡度条件下边坡安全系数。不同坡度对应的边坡安全系数如图7所示。

由图7可知，边坡安全系数随坡度的增大逐渐减小，坡度为35°、45°、55°、65°对应的边坡安全系数分别为：1.785、1.421、1.275、1.091。与坡度为35°相比，边坡安全系数减小量分别为0.364、0.51、0.694，分别增大了20.39%、28.57%、38.88%。坡度对边坡安全系数的减小效果分别为20.39%/10°（45°）、14.29%/10°（55°）、12.96%/10°（65°），说明坡度对边坡安全系数的减小效果随坡度的增大逐渐降低。

3.4 弹性模量对边坡稳定的影响

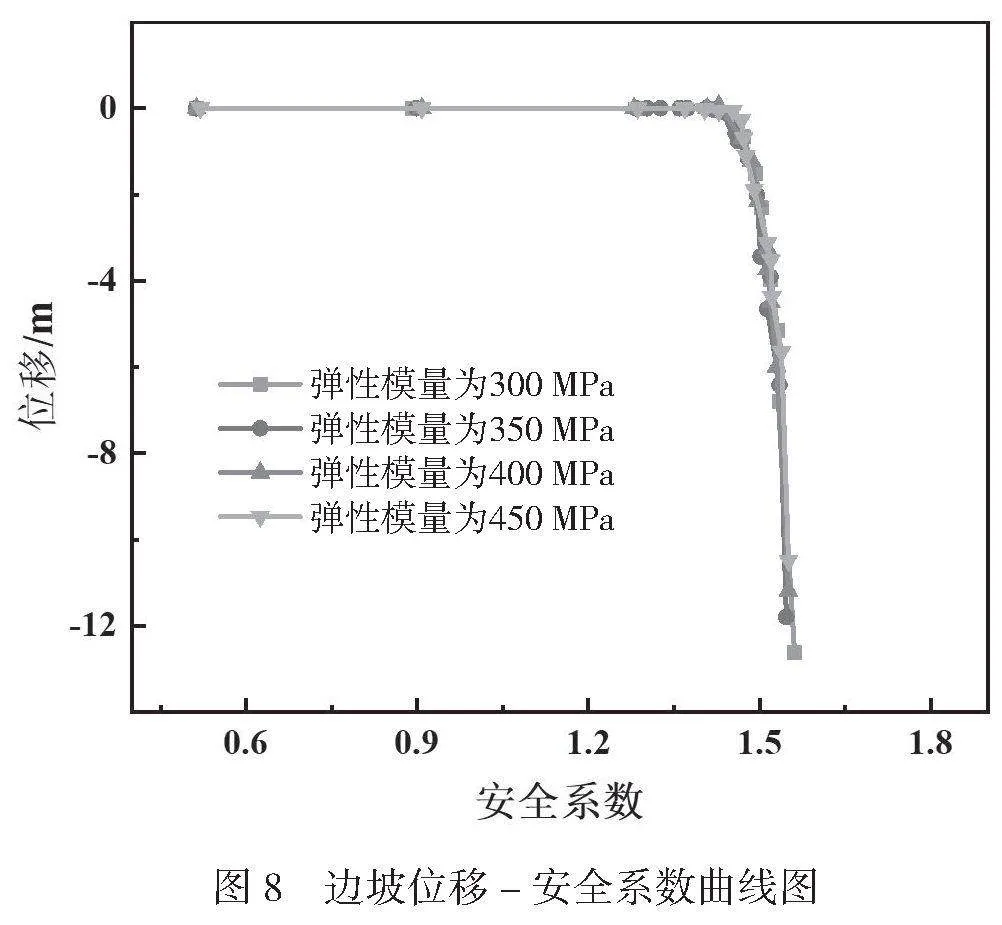
为研究不同弹性模量条件下边坡稳定性的变化规律，设置4种弹性模量梯度：300MPa、350MPa、400MPa、450MPa。得到不同弹性模量条件下边坡位移-安全系数曲线如图8所示。

由图8可知，4种弹性模量在强度折减过程中发生位移突变点基本一致，将位移突变点横坐标作为该弹性模量条件下边坡安全系数。对应的边坡安全系数均为1.421，说明弹性模量对边坡安全系数的影响较小。

综上所述，黏聚力、内摩擦角、坡度及弹性模量均会对泥岩边坡安全系数产生影响。但4种因素对泥岩边坡安全系数的影响规律存在差异，黏聚力、内摩擦角与泥岩边坡安全系数呈正相关，边坡坡度与泥岩边坡安全系数呈负相关，弹性模量对泥岩边坡安全系数的影响较小。

4 结论

本文以某软岩高边坡为研究对象，基于ABAQUS有限元软件，分析边坡稳定性，并研究边坡土体黏聚力、内摩擦角、坡度、弹性模量等对边坡稳定性的影响，得到以下主要结论。1）增大黏聚力，增大内摩擦角，减小坡度，泥岩边坡的安全系数越大；改变边坡弹性模量，泥岩边坡安全系数基本不发生变化。2）黏聚力35kPa、40kPa、45kPa、50kPa对应的边坡安全系数分别为1.393、1.421、1.503、1.558；与黏聚力为35kPa相比，黏聚力对边坡安全系数的增大效果分别为2.23%/5kPa（40kPa）、3.95%/5kPa（45kPa）、3.95%/5kPa（50kPa）；黏聚力对边坡安全系数的增大效果随黏聚力的增大先增大后趋于稳定。3）内摩擦角为20°、25°、30°、35°对应的边坡安全系数分别为1.356、1.421、1.552、1.644；与内摩擦角为20°相比，内摩擦角对边坡安全系数的增大效果分别为4.79%/5°（25°）、7.23%/5°（30°）、7.08%/5kPa（35°），内摩擦角对边坡安全系数的增大效果随内摩擦角的增大先增大后减小。4）坡度为35°、45°、55°、65°对应的边坡安全系数分别为1.785、1.421、1.275、1.091。与坡度为35°相比，坡度对边坡安全系数的减小效果分别为20.39%/10°（45°）、14.29%/10°（55°）、12.96%/10°（65°），坡度对边坡安全系数的减小效果随坡度的增大逐渐降低。5）弹性模量为300MPa、350MPa、400MPa、450MPa对应的边坡安全系数均为1.421，说明弹性模量对边坡安全系数的影响较小。

参考文献

[1]刘新喜，夏元友，蔡俊杰，等.降雨入渗下强风化软岩高填方路堤边坡稳定性研究[J].岩土力学，2007，（8）：1705-1709.

[2]李海洲，杨天鸿，夏冬，等.基于软岩流变特性的边坡动态稳定性分析[J].东北大学学报（自然科学版），2013，34（2）：293-296.

[3]何忠明，吴维，付宏渊，等.基于应变软化模型的软岩高边坡过程稳定性研究[J].中南大学学报（自然科学版），2013，44（3）：1203-1208.

[4]蒋中明，曾铃，付宏渊，等.极端久雨条件下软岩边坡动态稳定性分析[J].中国公路学报，2014，27（2）：27-34.

[5]姚文敏，胡斌，余海兵，等.三维软硬互层边坡的破坏模式与稳定性研究[J].工程科学学报，2017，39（2）：182-189.