某壳体液压爆破试验的分析与理论计算

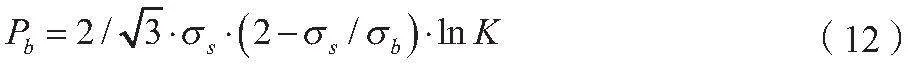
摘 要：本文介绍了薄壁壳体的液压爆破试验原理、试验方法和相应理论计算，对该类壳体爆破的试验具有指导意义。本文基于薄壁压力容器模型，详细分析了在承受均匀内压过程中椭球封头和中间筒体的应力状态，推导了径向和环向应力公式，确定了爆破发生的部位，深入认识了爆破发生的机理，并实测验证了选用Faupel经验公式进行理论爆破值的计算是准确的。

关键词：压力容器；爆破试验；径向应力；环向应力；理论爆破值

中图分类号：TH 49" " " 文献标志码：A

某薄壁壳体材料采用优质30CrMnSiA合金钢，由前封头、中间筒体和后封头等组焊后机加成形。工作过程中壳体中化学能转换成热能和压力能，壳体需要承受一定的压力，属于压力容器类零件。在满足生产需要的基础上，压力容器要安全、可靠，一旦失事，不仅会使容器和设备本身遭受破坏，还会破坏其他设备和建筑，甚至造成人身伤亡事故。由内部介质向外扩散带来的化学爆炸、着火燃烧或者恶性中毒等连锁反应更会造成不可估量的灾难性破坏[1]。于是，为了保障安全性，需要验证壳体的实际承载能力，每一批次壳体或者同批次壳体每生产50件进行一件液压爆破试验，并与理论爆破压力值进行比较。如果实际爆破压力值小于理论计算值，那么本批次壳体不合格。因此液压爆破试验是判断壳体是否合格的重要指标之一。

1 壳体爆破试验原理

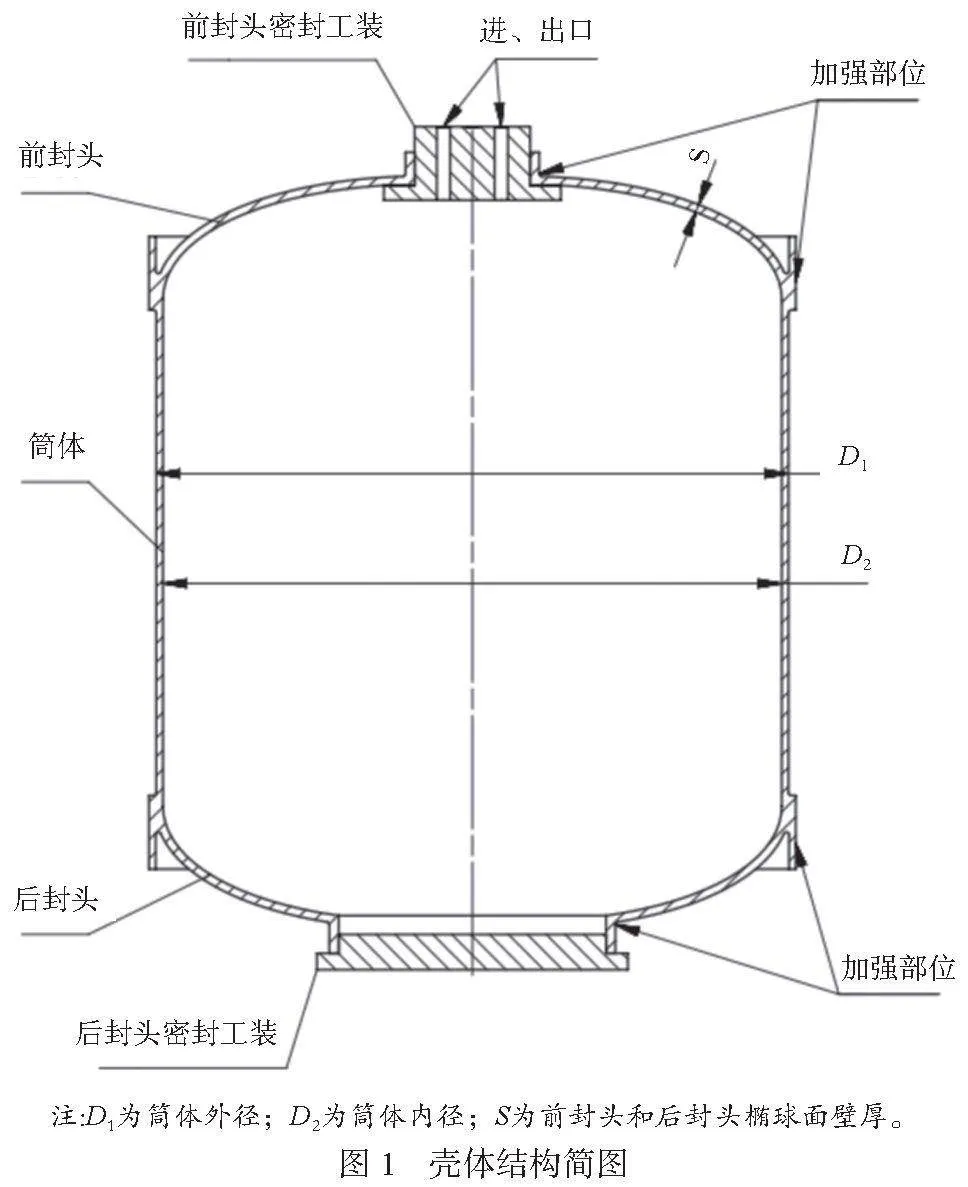
壳体的结构简图如图1所示。壳体的前、后封头有开孔，不是一个完整的封闭结构。因此无论是做密封试验还是液压爆破试验，均需要设计制作专用密封工装将壳体前、后封头开口密封，使密封后的壳体、水箱、增压泵、单项阀、可调节流阀、安全溢流阀、截止阀和压力表等构成一个静液压系统，其试验原理如图2所示。试验介质为浓度1.5%～2.5%的四硼酸钠水溶液，当系统无泄露后，关掉截止阀，按照一定速率向壳体缓慢增压。当壳体材料受均匀内压时不断发生形变，直到达到承受极限压力，壳体发生爆破。本试验属于高压破坏试验，具有一定危险性，增、泄压操作与检查都将采取隔离保护措施。

2 壳体应力分析

当壳体承受均匀内压时，壳体材料产生内部应力，当内部应力达到承载极限值时发生爆破。为了深入认识爆破发生机理，需要对壳体进行应力分析。由图1可知，将前、后封头密封工装与壳体封头开口装配后即构成一个封闭压力容器。因此可将整个壳体简化为一个中间为圆筒、两端连接前/后椭球封头的薄壁压力容器模型，压力容器壳体一般承受均匀的薄膜应力[1]。

2.1 椭球形封头应力分析

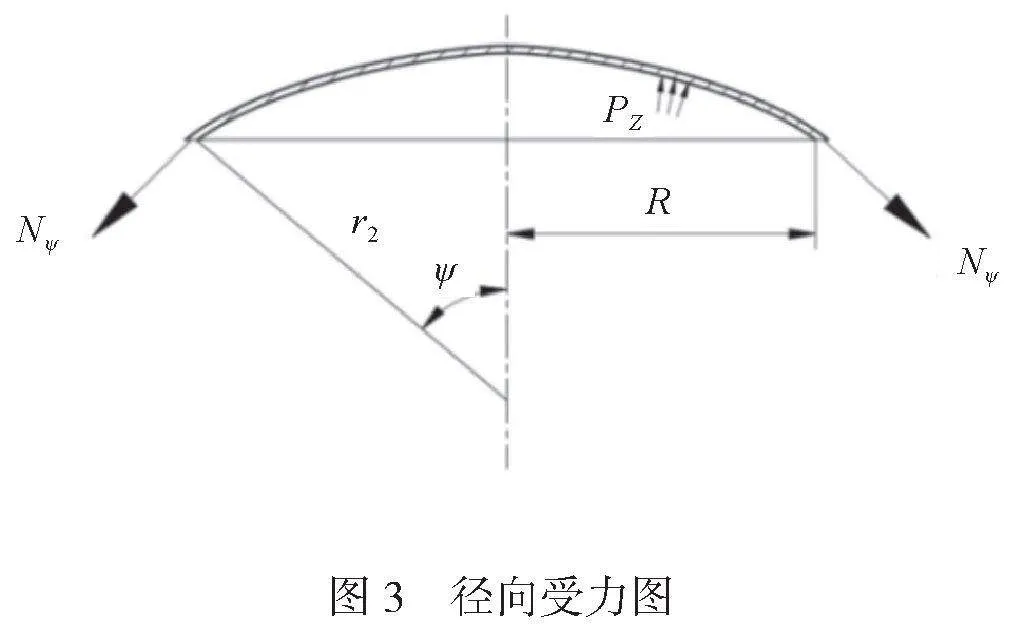
对于椭球封头径向薄膜应力分析，需要取椭球封头壳体上的任意横截面，如图3所示，并列出轴向整体力平衡方程式，如公式（1）所示。

2πRNψsinψ=πR2PZ" " " " " " " （1）

式中：R为横截面半径，m；Nψ为径向力，N；ψ为截面与此曲面的第二曲率半径r2与中心轴的夹角，°；PZ为壳体内压力，Pa；r2为第二曲率半径，m。

过遇转曲面上任意点，做垂直于该点所在径线的平面，使之与遇转曲面相交得到一割线，割线在该点的曲率半径即第二曲率半径[2]。由公式（1）可得径向力Nψ。

Nψ=RPZ/（2sinψ） " " " " " " " " " （2）

径向薄膜应力等于径向力除对应截面积，于是径向应力如公式（3）所示。

σψ=Nψ/S1 " " " " " " " " " " " " （3）

式中：σψ为径向薄膜应力，Pa；S1为截圆处的壳体径向截面积，与Nψ垂直，m2。

对于环向薄膜应力分析，需要从椭球封头壳体中取出一块单元体，如图4所示。径向力Nψ、环向力Nθ共同作用，以平衡内压PZ产生的向外载荷，于是可列出单元体的力平衡方程，如公式（4）所示。

Nψ/r2+Nθ/r1=PZ " " " " " " " " "（4）

式中：r1为椭圆面在截点的第一曲率半径，m。

第一曲率半径为径线上任意点的曲率半径，由公式（4）可得环向力Nθ，如公式（5）所示。

Nθ=r2（PZ-Nψ/r1） " " " " " " " " （5）

因此环向薄膜应力如公式（6）所示。

σθ=Nθ/S2 " " " " " " " " " " " " "（6）

式中：σθ为环向薄膜应力，Pa；S2为所取单元体环向截面积，m2。

如果a、b分别为椭圆的长短轴半径，曲线方程为y2=b2-b2x2/a2，可以推算出任意点处第一曲率半径和第二曲率半径，分别如公式（7）、公式（8）所示。

r1=[a4-x2（a2-b2）]3/2/（a4b） " " " " " "（7）

r2=[a4-x2（a2-b2）]1/2/b" " " " " " " "（8）

由上述分析可知，椭球形封头在内压作用下受径向和环向薄膜应力，沿径线各点的应力是变化的，顶点处应力最大。径向薄膜应力全为拉伸应力，而环向薄膜应力在靠近中心处，近似为在球面部分中产生环向拉伸薄膜应力，在封头与中间筒体过渡区中产生环向压缩薄膜应力。这种环向薄膜应力的分布规律可由标准椭圆封头在内压作用下的趋圆特征现象来理解。

2.2 中间筒体应力分析

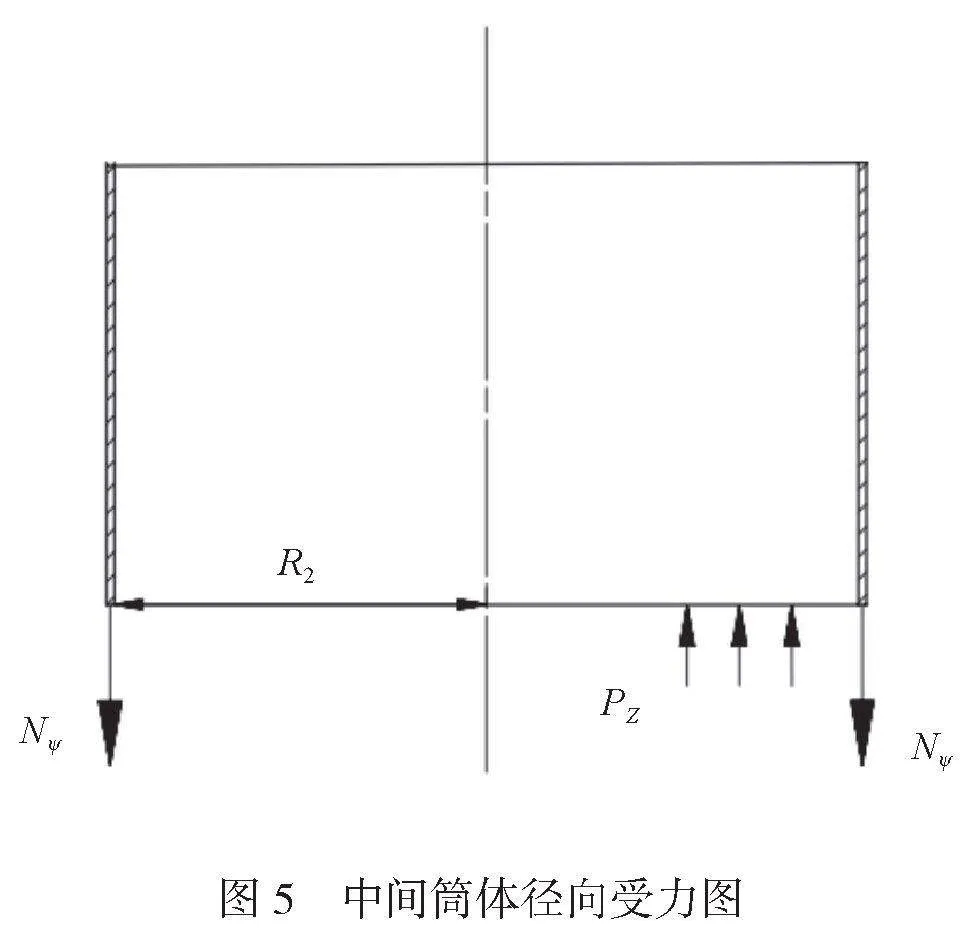
中间筒体的应力情况与椭球面情况一样，同样承受径向薄膜应力和环向薄膜应力。中间筒体径向受力如图5所示，由几何结构可知截面处半径R2为中间筒体的半径，R2=D2/2，其与圆筒间的夹角ψ为90°，带入公式（2）可以得出中间筒体的径向薄膜力Nψ，如公式（9）所示。

由第一曲率半径定义可知，该处的径线为直线，因此r1为∞大，第二曲率半径r2为中间筒体的横截面半径R2。由公式（4）和公式（5）可得中间筒体的环向薄膜力Nθ，如公式（10）所示。

Nθ=D2PZ/2=2Nψ " " " " " " " "（10）

将公式（9）和公式（10）分别带入公式（3）和公式（6），可以分别求出中间筒体的径向和环向薄膜应力σψ和σθ。

式中：δ为中间筒体的壁厚，δ=（D1-D2）/2，m。

由上述分析可知，中间筒体的环向应力是径向应力的2倍，这种薄膜应力是平衡内部压力所必须的，是由液压压力直接作用在圆筒上产生的应力，一旦发生屈服，就会造成整个筒体大变形。因此必须严格加以控制，其许用应力为1倍材料许用应力[3]，是壳体薄弱环节和容易发生爆破的部位。

2.3 加强部位应力分析

壳体开孔后，开孔的边缘应力分布极不均匀，在离开孔边缘较远处，应力几乎没有变化，而增大的应力集中分布在开孔的边缘[1]。由椭球封头和中间筒体薄膜应力的分布可知，在内压作用下，中间筒体和椭球封头连接区域的应力不一致，会造成两者连接点变形、不连续，在接头处会产生边界剪力和弯矩，同时也是焊接的薄弱区域。为了增强壳体的强度，如图1所示，在前、后封头中心开口处和中间筒体与椭球封头连接过渡区域进行加强设计，安全系数高于其他部位。

3 爆破试验简述

3.1 爆破过程分析

在壳体爆破过程中，塑性材料的应力/形变过程如图6所示。OA段为弹性阶段，壳体壁应力较小，会产生弹性变形。当压力失去后，变形可恢复。随着压力增大，应力和变形不断增加，A点表示内壁开始屈服，整个壳体的弹性行为到此终止。AB段为屈服阶段，壳体材料从内壁向外壁屈服，形变增加，应力不随之发生明显改变，B点表示壳体已进入整体屈服阶段。BC段为强化阶段，此时塑性变形会使材料强化，导致承载能力提高，厚度不断减少，造成承载能力下降，当达到极限承载压力C点时，会发生爆破，对应的压力值为爆破压力值。CD段为爆破阶段，对于塑性好的材料，在爆破过程中会裂开一条缝，裂口呈约45°剪切唇状，无碎片产生。

3.2 理论爆破压力值计算

现有的爆破压力公式有多种，常用的是Faupel公式、中径公式和基于扭转-剪切数据的公式，其中Faupel公式计算简单且在工程设计上应用方便，应用最广，对筒体爆破压力的计算有较高精度[4]，Faupel经验公式如下。

式中：Pb为理论爆破压力值，MPa；σs为材料屈服强度，MPa；σb为材料抗拉强度，MPa；K为外径与内径之比。

已知壳体材料30CrMnSiA的σs为835MPa，σb为1080MPa，中间筒体外径D1为469.6mm，内径D2为463mm，内、外椭球母线比分别为231.5/92.3和237/97，符合薄壁容器特征。由公式（12）可计算出中间筒体Pb为16.7MPa，椭球封头最小理论爆破值Pb为27.8MPa。由于椭球封头的壁厚大于中间筒体的壁厚，理论爆破压力值大于中间筒体的理论值是符合设计要求的。因此由理论分析和计算可知，爆破的部位应在中间筒体相对薄弱部位，爆破的理论压力值最小为16.7MPa。

3.3 试验步骤和结果分析

试验开始前检查试验设备和管路的完好性，将壳体注满水并静置，将液压系统的进出口与壳体进出口连接。在壳体加压前，应采用反复低压加载，把受试壳体和承压管道内的空气全部排尽，并确认试验系统无泄漏[5]。在压力值升至2.0MPa±0.2MPa后，保压5min，检查壳体和管路接头有无泄漏，无泄漏后继续升压至13.4MPa±0.2MPa，保压1min。检查壳体和管路接头有无泄漏，如果无继续升压直至爆破，记录最终爆破瞬间压力值。

经多次爆破试验实测，压力值为16.8MPa～17.5MPa，表明壳体的实际承压能力大于设计理论值且理论计算值与实测值相差＜5%，证明运用Faupel经验公式计算理论爆破压力值是准确的。而实际不同壳体爆破值的差异主要是壳体热处理后材料力学性能有个体差异，原因是该壳体材料热处理后需要满足σb≥1080MPa，由公式（12）可知，σb越大，理论爆破压力值相应增大，并且中间筒体内径和外径存在加工尺寸范围，内、外径比值K增大，理论爆破压力值随之增大。爆破裂口呈剪切唇状，无碎片产生。爆破口在中间筒体中段位置，并沿径向裂开，壳体的其他部位没有主动开裂现象，爆破的部位和破口形态说明符合上述分析。

4 结论

该文分析了壳体爆破试验的原理和试验方法，主要介绍了当承受内压时，壳体各部分的应力分布状态，推导了相应的理论计算公式，预估了爆破发生的部位，并选用Faupel经验公式来计算此类壳体的理论爆破压力值。上述分析和计算具有以下3个方面的实际意义。1） 可指导此类壳体的爆破试验，测定实际爆破压力值，分析爆破部位，将其作为判断批次性壳体是否合格的一个重要指标。2） 可指导该类壳体结构参数的优化设计。3） 验证了选用Faupel经验公式来计算此类壳体的理论爆破压力值是准确的。

参考文献

[1]魏锋.压力容器设计知识[M].北京：化学工业出版社，2005.

[2]催克清.安全工程大辞典[M].北京：化学工业出版社，1995.

[3]梁琳.压力容器壳体元件强度计算方法浅析[J].石油化工设计，2003，30（2）：20.

[4]周波，於孝春.标准椭圆形封头爆破压力的计算[J].工业安全与环保，2010，36（9）：43.

[5]全国气瓶标准化技术委员会.气瓶水压爆破试验方法：GB/T15385—2011[S].北京：中国标准出版社，2012.