GeoGebra环境下基于认知负荷理论的立体几何教学实践

[摘 要] 立体几何知识具有较强的关联性和抽象性，传统教学模式难以将其直观地传递给学生，导致学生无法清晰理解图形的空间布局及其元素间的关系，从而产生较高的认知负荷. 因此，基于负荷产生的原因，通过GeoGebra软件的动态展示功能，探索并优化立体几何教学中认知负荷的策略. 文章以“基本立体图形”教学为例，依据策略制定实验教学方案，并对实施效果进行分析评估.

[关键词] 认知负荷理论;GeoGebra;立体几何;基本立体图形

《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》（下文简称“双减”）一经发布，便迅速吸引了中国教育界的广泛关注. “双减”政策明确指出“确保学生在校内学足学好”，这表明“双减”政策的主阵地是课堂. 作为“双减”政策的执行者，教师必须认识到课堂的关键作用，并学会优化教学方法[1]. 在高中立体几何的教学中，传统的教学方式难以直观传授相关知识. 探究其根本原因，在于立体几何知识固有的高度抽象性和思维的隐蔽性，这导致学生在学习过程中面临较大的认知负荷. 因此，教师可以借助动态数学软件辅助立体几何教学，将知识外显化，思维可视化，以实现减负增效.

《普通高中数学课程标准（2017年版2020年修订）》针对立体几何的教学提出了明确要求，即教师应借助实物模型或计算机软件来展示空间图形，以便学生能够更好地理解空间图形的结构特性，并掌握在平面上表示空间图形的方法与技能[2]. 面对复杂且抽象的立体图形，学生在学习过程中常常面临较高的认知负荷，这是影响学习成效的关键因素，也是教师在立体几何教学中必须解决的问题. 如何借助数学软件，将立体几何中高度抽象性和复杂关联性的知识内容，以直观的方式呈现给学生，无疑是一项艰巨的挑战.

认知负荷理论与GeoGebra软件

在1988年，教育心理学家斯威勒（John Sweller）及其同事提出了认知负荷理论. 该理论认为，在学习或解决问题的过程中，学习者的大脑工作记忆对学习材料进行加工，其资源是有限的;与此同时，大脑的长期记忆则用于储存已知的加工编码信息，其资源则是无限的. 在工作记忆对学习内容进行信息处理和存储的过程中所消耗的认知资源，被称为认知负荷[3]. 总认知负荷由内在认知负荷、外在认知负荷以及关联认知负荷三个部分组成. 内在认知负荷由知识内容和学习者现有水平决定，当学习材料繁杂，学习者缺乏相应认知水平，信息加工时会产生较高内在认知负荷，加重学习负担[4]. 外在认知负荷由教学设计决定，若教学材料的组织不当，会导致外在认知负荷过高，阻碍学习. 关联认知负荷由学习者的学习兴趣和动力决定，是有利的认知负荷[5]. 三种认知负荷的和就是总认知负荷. 为了确保学习效率，总认知负荷必须低于工作记忆中可用的认知资源容量. 一旦总认知负荷超出工作记忆所能承受的范围，学习者将面临认知困难，这将对学习成效产生负面影响.

在教学领域中，以认知结构为基础，工作记忆的有限性为核心的认知负荷理论，是影响力最大的理论框架之一[6]. 在教学过程中，降低内在认知负荷和外在认知负荷，同时增加相关认知负荷，是至关重要的. 这样可以确保学习者所承受的认知负荷总量达到最优化水平，从而促进有效学习的发生. 对于高中数学中那些复杂且高度抽象的知识点，单纯依靠教师的口头讲解、板书和实物模型的传统教学方法，显然无法充分优化学生所经历的认知负荷. 然而，动态数学软件凭借其3D动态呈现功能，能够有效地减轻认知负担并提高学习效率. 因此，“将动态数学软件作为优化学生认知负荷的有效工具”已成为一种必然趋势.

在2002年，美国亚特兰大大学的数学教授Markus Hohenwarter开发了动态数学教学软件GeoGebra. 这款软件集几何绘图、代数运算和数据处理等多种功能于一体，是动态数学学科的重要工具. GeoGebra的两大显著特点在于：首先，它能够同步展示几何图形与代数方程的变化，实现图形与代数的无缝对接，极大地丰富教学资源;其次，软件中的代数区、3D绘图区、工作表和运算区等多个模块之间能够相互关联和互动，确保教学材料的直观展示[7]. 在高中数学教学领域，GeoGebra相较于其他数学软件而言，拥有开源免费、易于学习以及强大的3D绘图功能等显著优势. 其卓越的3D展示能力能够从多个角度生动地呈现立体图形的空间结构及其形态变化，有效地将抽象的数学概念具体化. 通过“数”与“形”的同步变化，学生能够构建起代数与几何图形之间的联系，使得数学知识的内在关联性变得直观且易于操作[8]. 应用软件能够使学生内隐的数学思维变得显性，从而直观地感知学习材料，并进一步优化认知负荷.

GeoGebra环境下优化认知负荷的立体几何教学策略

依据认知负荷理论，探讨三种认知负荷的成因，以GeoGebra软件作为降低认知负荷的有效手段，在立体几何教学过程中减轻内在和外在认知负荷，同时提升关联认知负荷. 通过参考图1所示的策略，可以优化总体认知负荷.

1. 结合教学内容使用GeoGebra，分解内在认知负荷

内在认知负荷是原生性负荷，主要取决于教学内容的复杂性以及学习者当前的知识水平. 在立体几何教学中，面对复杂且抽象的教学内容，可以通过将教学内容细分为若干主题来简化教学. 对于选定的主题，进一步规划教学目标、教学方法和课时分配，从而明确各个阶段的教学任务. 一方面，通过合理安排教学课时和细化教学目标，可以减少学生需要处理的信息量及其相互作用，从而降低内在认知负荷. 另一方面，将GeoGebra软件的运用融入教学，采用过程化的教学手段，将原本隐性的知识转化为显性，揭示不同元素之间的联系，这有助于知识的迁移和理解，进一步减轻学生的内在认知负荷.

2. GeoGebra直观展现学习材料，降低外在认知负荷

外在认知负荷是由于教学材料设计不当而造成的无效认知负荷. 在设计教学时，若难以直观形象地呈现学习材料，学生可能难以领会材料中各元素的含义，也难以梳理这些元素之间的联系，这可能导致他们面临较高的外在认知负荷. 为了减轻外在认知负荷，教学设计时应从展示角度和形式等多个维度优化学习材料的呈现方式. 适时运用GeoGebra的3D绘图和数形同步变化等功能，以科学和直观的方式展示学习内容，通过视觉化手段帮助学生直观地感知材料中的元素特征及其逻辑关系，确保学习内容的适宜呈现，从而降低外在认知负荷.

3. 选择恰当的教学方法，增加关联认知负荷

关联认知负荷，作为一种对学习有益的负荷，具有双重正面效应. 首先，它通过提供内容丰富、形式多样的课堂环境，能够调整学生的心态，激发他们的学习热情，从而增加关联认知负荷;其次，运用多样化的教学方法能够进一步提升学生的学习兴趣和动力，同样有助于增强关联认知负荷. 例如，在应对枯燥且复杂的立体几何知识时，利用GeoGebra的动态演示功能，采用演示法教学，可以有效提升学生的专注度. 同时，借助GeoGebra设计的情境活动，结合情境教学法、启发式和探究式教学法，能够激发学生在积极参与的教学环境中产生持续的认知动力. 将GeoGebra软件融入教学过程，有助于营造积极的课堂氛围，进而激发学生内在的学习动机，并增加其关联认知负荷.

GeoGebra环境下基于认知负荷理论的“基本立体图形”教学

在《在一般观念引领下探索空间几何图形的性质（续）——“立体几何初步”内容分析与教学思考》一文中，章建跃强调信息技术在立体几何教学中的关键作用. 例如，通过使用数学软件绘制长方体，并借助动态演示技术，可以从多个角度观察其结构特征，从而清晰地理解点、直线和平面之间的位置关系[9]. 课程标准在立体几何章节首次引入了“基本立体图形”的概念. 这些立体图形源于现实世界物体的抽象化，学生通过观察周围环境中的具体几何体，能够深入理解基本立体图形的结构特征，从而抽象出空间图形的基本元素及其位置关系. 然而，高中生在学习基本立体图形时，往往受到平面几何知识的负迁移效应、空间想象力的不足以及学习兴趣的缺乏等多重主观和客观因素的影响，这使得他们在认知上面临一定的挑战. 为了更有效地利用信息技术，需要找到方法，将这些高度抽象且关联复杂的立体图形知识，以一种易于学生理解和接受的方式传授给他们. 依据上述教学策略，笔者设计了在GeoGebra环境下基于认知负荷理论的“基本立体图形”教学方案.

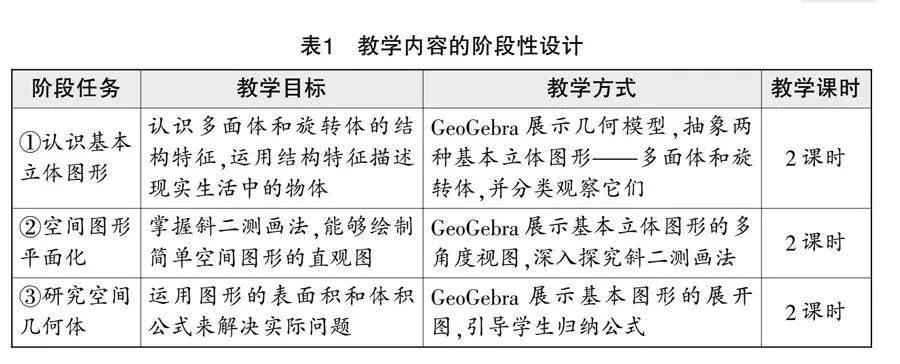
1. 教学内容的整体设计

“基本立体图形”教学内容包括三节：基本立体图形、立体图形直观图、简单几何体的表面积与体积. 在教学设计时，应重视探究各种几何体的构建过程，并从其结构特征着手，清晰地界定空间几何体中点、线、面之间的相互关系. 在教学时，应遵循“定义—平面表示—面积与体积”的研究路径，按照从具体实例到抽象概念的顺序，将教学分解为3个阶段. 表1详细描述了这些阶段任务.

2. 学习材料的呈现方式

在第一阶段，学生在认识基本立体图形的过程中，可以借助GeoGebra软件来展示棱柱、棱锥和棱台的各个点、线、面. 这有助于学生清晰地理解数量关系以及图形之间的联系. GeoGebra软件还能生动地演示圆柱、圆锥、圆台和球体的形成过程，使学生能够直观地感知空间几何体的构建，从而加深对这些基本立体几何图形模型的理解.

进入第二阶段，当学生开始学习空间几何体的直观图时，GeoGebra软件可以用来展示一个简易模型，例如窗户在地上影子的变化，从而引入斜二测画法的概念.

到了第三阶段，为了深入理解空间几何体的表面积和体积，GeoGebra软件能够直观地展示圆台的展开图，帮助学生探究圆台的表面积计算. 此外，通过GeoGebra呈现的3D动态图象，学生可以研究球体的体积公式，并领会极限化和以曲代直的数学思想.

根据每个教学阶段的具体任务，从展示角度和形式等多个维度，科学地优化学习材料的呈现方式.

例如（见图2），通过操作滑动条，学生能够动态观察圆台的展开过程，从而归纳出圆台的表面积公式. 通过改变圆台的展示形式，有助于降低学生的外在认知负荷.

3. 教学方法的选择

在第一阶段，利用GeoGebra展示物体的3D模型，初步探究立体几何知识，增强学生的学习体验，激发学生的兴趣. 进入第二阶段，先观察实物正方体，随后利用GeoGebra展示正方体，引导学生尝试在纸上画出正方体的平面图，从而增强学生的成就感. 到了第三阶段，当探讨柱体、锥体和台体的表面积公式时，鼓励学生亲自上台展示这些立体几何图形的展开图，从而更深入地理解立体几何图形的表面积公式. 在整个主题学习中，注重将日常生活中的实际情境与数学知识相结合，运用问题驱动法、探究教学法和启发式教学法，激发学生的学习热情并提升他们的内在学习动力.

例如（见图3），在GeoGebra环境中通过操作正方体模型来观察其截面. 正方体中的红点可以拖动，允许用户将其放置在正方体不同棱的不同位置上，有助于探索正方体的各种截面，从而激发学生的求知欲，并增强其对几何结构的理解和认知.

实验与分析

1. 研究问题

本研究的目标是探究“相较于传统教学方法，运用认知负荷理论指导并利用GeoGebra软件设计的教学活动是否能更有效地深化学生对基本立体图形的理解？”研究假设提出：基于认知负荷理论，在GeoGebra软件环境中设计的教学活动相较于传统教学，将更有利于提升学生对基本立体图形的理解.

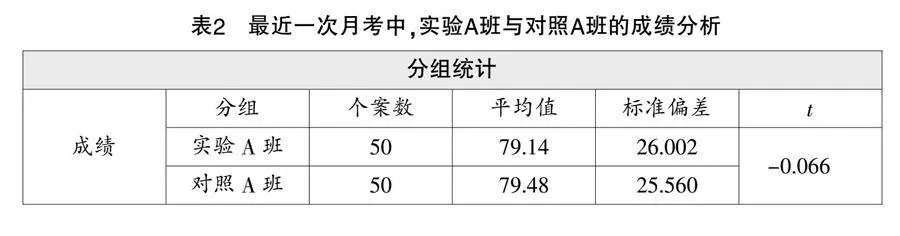
2. 研究对象

研究对象是枞阳县某学校高一年级中近一次月考班级数学成绩相近的两个平行班，共100名学生. 其中，实验A班50人，对照A班50人. 两个班级的学生性别比例相当，平均成绩也相近. 运用SPSS软件对这两个班级学生最近一次月考成绩进行独立样本t检验，结果见表2. 由于两个班级的水平没有显著差异，因此它们都适合作为实验对象. 实验A班和对照A班的数学教学，均由原班级的同一位数学教师负责进行.

3. 研究过程

实验时间为两周，教学课题为基本立体图形，总共7个课时，其中6个课时用于教学实验，1个课时用于后测，实验A班和对照A班最近一次月考成绩用于前测. 实验A班采用GeoGebra软件辅助的认知负荷理论指导下的实验教学方法，而对照A班则继续采用传统的教学方法，不涉及任何动态数学软件的应用.

在开展教学实验之前，两个班级的参与学生已经在初中阶段掌握了平面几何知识以及部分立体图形的相关知识，并能够分析图形的运动和变化属性.

实验A班的教学设计主要基于之前提及的认知负荷理论，将本单元教学划分为3个阶段. 实验A班的教学从对基本立体图形的分类认识入手，在GeoGebra软件环境中，重点培养学生对基本立体图形结构特征的直观感知，并通过操作探究空间几何体. 教学分为3个阶段，共计6个课时，内容包括以下6个课题.

（1）多面体的结构特征. 借助GeoGebra软件，直观感知多面体（包括棱柱、棱锥和棱台）的点、线、面及其相互关系，并归纳和抽象出多面体的结构特征.

（2）旋转体的结构特征. 借助GeoGebra软件，直观感知旋转体（包括圆柱、圆锥、圆台、球）的点、线、面及其相互关系，并归纳和抽象出旋转体的结构特征.

（3）平面图形的直观图. 学习直观图的概念，通过观察窗户和地面的影子随时间的变化，以及稻田在远距离视角下的形状变化，引入斜二测画法;学会绘制水平放置的平面图形（包括圆、正方形、平行六边形）的直观图.

（4）几何体的直观图. 在掌握斜二测画法和画平面图形的基础上，尝试绘制立体图形（正方体、正六棱柱、圆柱、球、简单组合体）的直观图. 概括绘制空间立体图形的步骤：画出轴线、底面、侧面.

（5）多面体的表面积和体积. 利用GeoGebra软件展示多面体的展开图，促使学生理解多面体的表面积是围成多面体各个面的面积之和;掌握棱柱、棱锥、棱台的表面积公式，并运用公式计算它们的表面积;理解棱柱、棱锥、棱台的体积公式，根据条件计算底面面积和高，运用公式求解多面体的体积.

（6）旋转体的表面积和体积. 利用GeoGebra软件展示圆柱、圆锥、圆台的侧面展开图，以及侧面展开图中各线段与原旋转体的关系，促使学生灵活运用圆柱、圆锥、圆台的表面积公式，理解并掌握圆柱、圆锥、圆台、球的体积公式.

对照A班采用的是传统教学方法. 教师首先引导学生观察教材中的物体，让他们识别形状，并引导他们总结出多面体与旋转体的定义. 在黑板上，教师绘制棱柱、棱锥、棱台、圆柱、圆锥、圆台以及球体，并详细讲解它们的定义和结构特点. 接着，学生通过观察魔方（正方体），理解直观图的概念，并通过平行投影来研究斜二测画法，学习运用这种画法来绘制几何体. 最终，学生掌握简单几何体的表面积和体积公式，并运用这些公式进行实际计算.

4. 数据收集

本次研究选取了实验A班和对照A班最近一次月考的成绩作为前测数据，同时以针对基本立体图形单元主题的试卷测验成绩作为后测指标. 试卷内容涵盖几何体的主要结构特征、斜二测画法、空间几何体直观图的绘制，以及简单几何体及其组合体的表面积和体积计算等知识点. 在收集并整理了两班学生实验后的成绩数据后，笔者运用独立样本t检验方法，对实验A班与对照A班学生在成绩上的差异进行了显著性分析.

5. 实验结果分析

运用SPSS软件，得到表3所示的实验结果. 从表3可以看到，实验后实验A班与对照A班在主题单元测试的平均成绩分别为89.70和79.50. 通过独立样本t检验，发现p<0.05，这表明实验A班与对照A班在实验后的成绩上存在显著差异. 从实验结果可以看出，在GeoGebra环境下，依据认知负荷理论设计的教学方法，对于促进学生对基本立体图形的理解以及提升他们的数学成绩具有积极效果.

讨论

目前，绝大多数关于GeoGebra软件的教学研究仅限于以认知理论为基础进行分析或调查，鲜有研究将认知理论与GeoGebra软件相结合，在数学教学实践中探索其对学生数学成绩的影响. 然而，通过GeoGebra软件的绘图功能，可以直观地展示复杂的立体几何概念，从而优化学生的认知负荷. 此外，现有研究已经表明，GeoGebra软件能够降低内在认知负荷和外在认知负荷，增加关联认知负荷. 这表明，合理运用GeoGebra等信息技术工具，能够平衡认知负荷的总量，并有助于提升教学效果[10].

根据认知负荷的产生原因和GeoGebra软件的特点，从原因出发，借助GeoGebra软件强大的3D绘图功能和几何代数同步展现特点，分解内在认知负荷、降低外在认知负荷、增加关联认知负荷，形成GeoGebra环境下优化认知负荷的策略. 依据策略设计并执行基本立体图形的教学实验. 实验结果显示，实验A班学生的总体成绩相较于对照A班有显著提升. 这一成效归因于在立体几何的入门学习阶段，高中生在处理复杂且抽象的空间几何体时，往往面临过大的认知负荷，这会干扰学习效率. 对于特定学习内容，记忆中存在一个理想的认知负荷量. GeoGebra软件通过将平面几何知识与立体图形相结合，分解内在认知负荷，并通过直观展示三维图形减少外在认知负荷. 此外，通过实验操作激发学生的学习兴趣，进而增加关联认知负荷. 这种优化总认知负荷的方法，能有效提升教学效果.

研究成果表明，在GeoGebra软件的支持下，基于认知负荷理论的教学方法在立体几何教学中显示出适用性. 该方法通过调整和优化学生的认知负荷，能在一定程度上有效提高学生的数学成绩. 本次教学实践探索将认知负荷理论与GeoGebra软件相结合，应用于数学课堂的可能性，为信息技术与数学教学的整合提供了有益的参考. 此外，从认知负荷的角度出发，本研究还提出了在GeoGebra环境下优化学生认知负荷的立体几何教学策略，旨在激发更广泛的思考，为数学和物理教学中GeoGebra的应用开拓新的视角.

参考文献：

[1] 中华人民共和国教育部. 中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》[EB/OL].（2021-07-24）[2022-04-18].http：//www.moe.gov.cn/jyb_

xxgk/moe_1777/moe_1778/202107/t20210724_546576.html.

[2]中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）[M]. 北京： 人民教育出版社，2020.

[3] 蒋荣清. 基于认知负荷理论的数学课堂教学策略[J].数学通报，2018，57（1）：39-42+46.

[4] 杨丽恒，原文志，马建宏. 基于认知负荷理论的数学“翻转课堂”教学模式探究[J]. 教学与管理，2015（21）：102-104.

[5] 于泠，陈波. 认知负荷理论指导下的并行计算实验教学探究[J]. 计算机教育，2016（12）：77-80.

[6] 张慧，张定文，黄荣怀. 智能教育时代认知负荷理论发展、应用与展望：“第十一届国际认知负荷理论大会”综述[J]. 现代远程教育研究，2018（6）：37-44.

[7] 张志勇. 高中数学可视化教学：原则、途径与策略：基于GeoGebra平台[J]. 数学通报，2018，57（7）：21-24+28.

[8] 罗建宇. 从融合到创新：基于Geo-Gebra的数学深度教学[J]. 数学通报，2020，59（2）：23-26.

[9] 章建跃. 在一般观念引领下探索空间几何图形的性质（续）：“立体几何初步”内容分析与教学思考[J]. 数学通报，2021，60（3）：2-7+21.

[10] 毛禧雯，何亚婷，李志伟. 认知负荷理论和GeoGebra的数学教学策略[J]. 宁德师范学院学报（自然科学版），2022，34（3）：322-326+336.