有规律加法算式问题的解决与早期代数思维培养的研究（上）

【摘 要】从一组有规律加法算式中归纳出一般化规律的过程，体现了学生早期代数思维的发展情况。通过测试和分析二、三年级学生解决“有规律加法算式问题”的情况，发现学生在具体的算术运算上的正确率约为95%，然而，当他们需要归纳一般化规律并用这些规律解决问题时，正确率就明显下降。通过对学生表达规律的能力进行分析，并根据揭示算式规律需综合考虑的三个具体方面，将学生的规律表达能力从低到高划分为三个水平层次。在具体表达时，学生可能表现出无法观察或发现规律，缺乏表达规律的能力，或者过分重视变化量而忽视了对不变量的描述等特点。

【关键词】有规律加法算式；早期代数思维；一般化规律

一、问题的提出

让二、三年级的学生去解决一组有规律加法算式的问题，如“32+3=£，32+6=£，32+9=£，……32+£=£”，要求他们先完成填空，再写一写有什么规律及说明自己的思考过程。在解决这样的问题中，学生需要仔细观察每一个算式，从这些多样化的算式中提炼出它们的共性和相互关系，进而将这些多样化的算式“压缩”为一个统一的模式，得出一般化的规律。这一过程是学生萌生早期代数思维的体现。能够准确写出一般化规律的学生，往往展现出较强的代数思维能力。

那么，二、三年级的学生在解决这类“有规律加法算式问题”时，他们的正确率是多少？正确的填空思路又有哪些？学生对于规律的表达呈现出哪些特点？其表达可以分为哪些水平层次？本文试图通过实证研究来解释这些问题，并通过对调查结果的分析，为小学数学早期代数思维教学提供启示与建议。

二、研究对象与测试过程

本研究对象选取二、三年级各一个班级，学生人数分别为37人和40人。为确保研究的代表性，笔者依据学生上一学期期末检测成绩，选择了二、三年级中处于中等水平的班级作为测试对象。测试过程要求每个学生需在30分钟内独立完成答题任务（若学生提前完成，允许提前交卷）。待所有学生完成答题任务后，笔者随机抽取部分进行访谈，测试与访谈在同一个半天内完成。

三、测试内容

具体测试题目如下。

1.观察算式，在方框里填上数。

2.第五行中的两个方框中，你填入的两个数是（ ），（ ），你为什么填入这两个数？（要写出你是怎么想的）

3.第十行中的第1个方框你填的数是（ ），你是怎么想的？请把你的想法详细地写一写。

4.第十行中的第2个方框你填的数是（ ），你是怎么想的？请把你的想法详细地写一写。

5.你觉得，这个题目中的算式是否有规律？如果有，请写一写是怎样的规律。

6.写一写题目中的“省略号”表示什么意思。

四、测试结果与分析

（一）填数正确率及分析

学生的填数正确率直接体现了他们的计算、发现规律及应用能力。通过对测试答卷的批改、统计与分析，得出以下测试结果。

1.二、三年级学生第一行至第四行填数的正确率均高达95%。这些题目属于学生根据给定要求，正确计算两位数加两位数的问题。测试结果表明，对于大多数二、三年级学生而言，他们能够很好地理解这种带有方框表达的问题，并清晰地把握题目的意图，即要求对“26与42、45、48、51”进行分别求和。同时，大多数学生在两位数加法的计算上展现了扎实的基础。值得注意的是，三年级学生的正确率并未显著高于二年级学生。

2.第五行填数的正确率二年级学生为81.08%，三年级学生为92.50%。与前面第一行至第四行填数的正确率相比，二、三年级学生填数的正确率分别下降了13.51%和2.50%。值得注意的是，三年级学生的正确率比二年级学生高出约10%。从学生的解题思路分析来看，正确解决第五行填数问题主要有以下两种思路。

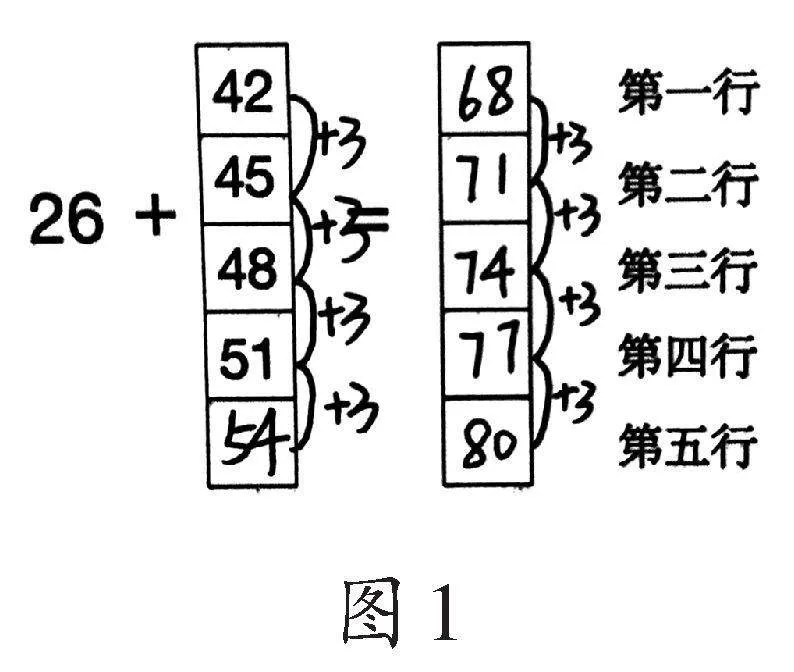
第一种思路：在第五行的两个方框中，左边一个方框是未知的加数，右边的一个是相应的和。学生根据题目中已知的加数42、45、48、51数列，发现并应用从上往下依次递增3的规律，从而得到第五行左边方框这个未知的加数是54（即51+3=54）。类似地，学生根据已经填出的和68、71、74、77数列，得到第五行右边方框填入的数是80（即77+3=80）。运用这种思路正确解决问题的二、三年级学生数分别占总人数的56.76%、62.50%。图1是一名二年级学生的解题过程。

第二种思路：填第五行左边的方框，即填未知加数时，与第一种思路相同，也是根据已知加数数列的规律得到54。但在填右边的方框，即填和时，通过计算26+54得到和是80，运用这种思路正确解决问题的二、三年级学生分别占总人数的18.92%、27.50%。

除了以上两种正确的解题思路外，二、三年级学生中分别有5.40%、2.50%的学生写出了正确答案，但未提供解题思路或思路表达不清晰。

3.如果说正确填写第五行两个方框中的数视为对规律的“近应用”，那么在第十行的方框中填入正确的数则表示对规律的“远应用”。统计结果显示，二、三年级学生第十行填空的正确率分别为32.43%和62.50%。三年级学生的正确率比二年级学生高出30.07%，这表明三年级学生的水平明显高于二年级学生。与填第五行的正确率相比，二、三年级学生在解决这一问题时的正确率分别下降了48.65%和30.00%，这说明对于许多学生来说，“远应用”是具有挑战性的。与填写第一行至第四行的正确率相比，二、三年级学生分别下降了62.16%和32.5%，这表明学生在计算两位数加法方面的能力远超于发现与应用规律解决问题的能力。从学生的解题思路分析来看，正确解决第十行填数问题主要有以下两种思路。

第一种思路：基于前五行算式中发现的规律，继续推导出第六行至第九行算式中的未知加数与相应的和，即逐一列举出第五至第九行中的数，再应用规律写出第十行两个方框中的数。二、三年级学生运用这种思路解决问题的正确率分别是21.62%和32.50%。图2是一名三年级学生写出第六行至第十行的结果和思考过程。

第二种思路：首先概括出算式中“未知的加数”以及“相应的和”与行数之间的对应关系，然后利用这种关系来解决问题。图3展示了一名三年级学生在填写第十行第1、2两个方框中数的解题思路。该学生以第五行为起始行，第1个方框中的数从第五行的54开始推算。从第六行到第十行共有5行，每行的数都比上一行增加3，因此增加了3×5=15，从而得到第十行第1个方框中的数为54+15=69。类似地，计算出第十行第2个方框中的数。

二、三年级学生运用这种思路解决问题的正确率分别为5.40%、30.00%。在运用这种思路解决问题时，学生在表达思考过程时通常仅使用数与相应的算式，而没有使用其他语言、图形或符号来辅助表达思考过程。

（二）规律表达情况及分析

为了准确揭示这组算式的规律，必须综合考虑以下三个方面：（1）一个加数不变，即一个加数为26不变。（2）另一个加数从上往下逐行递增3。（3）相应的和也随之逐行递增3。这三个方面的内容（以下简称“表达三内容”）共同构成了规律的完整表达。在“表达三内容”中，（1）体现了不变量的表达，而（2）和（3）则描述了变化量的表达。根据学生在表达中涉及“表达三内容”的程度以及表达的逻辑性，笔者将学生的表达水平从低到高划分为三个水平层次。

水平0：这是表达水平的最低层次，包括三种情况。（1）未能识别出规律；（2）未尝试表达规律（空白）；（3）在表达中未涉及“表达三内容”中的任何一个内容。在二、三年级学生中，分别有10人和3人处于这一水平，分别占总人数的27.03%和7.50%。这些学生的问题是未能观察到或表达出规律。

水平1：在这一水平的表达中，学生仅涉及“表达三内容”中的一个或两个方面的内容。二、三年级中处于此水平的学生人数分别为27人或36人，分别占总人数的72.97%和90.00%。具体情况如下。

1.没有学生能够表达出“不变量”，即在水平1的学生中，没有人指出类似“一个加数26不变”这一关键点。

2.在“表达三内容”中，只关注到单一个方面内容的学生，二、三年级分别有23人和25人，分别占总人数的62.16%和62.50%。这些学生在表达规律时只写出“表达三内容”中的一个方面内容，仅提及了“另一个加数的变化”这一个变化量。也就是说，既没有学生写出“不变量”，也没有学生写出“和的变化”这一个变化量。在写出加数这个变化量时，有的学生是十分具体表达规律的，如图4所示。也有学生会写出相对一般的“加数都是增加3”这样的规律。

3.分别有10.81%、27.50%的二、三年级学生同时写出了两个变化量。

图5是一个学生写出了两个变化量的表达。

可见，处于水平1这一层次的学生，表达规律的特点是重视对变化量的刻画，而忽视对不变量的描述。

水平2：当学生的表达同时涉及“表达三内容”三个方面的内容时，笔者将其划分为水平2。遗憾的是，仅有1名三年级学生在表达规律时达到这一水平。这个学生的表达如图6所示。

从图6中可以看出，这个学生采用“图与文字”相结合的方式来表达规律。左边带有方框的图中，他写出了不变量26以及另一个加数与和的变化规律。而右边的文字则描述了变化量的方向。令人遗憾的是，在右边的文字表达中，既没有提及不变量26，也没有表达出“依次增加3”的规律。这个学生是否注意到了26？为什么在文字表达中未提及这个不变量呢？笔者对他进行了访谈，主要的对话如下。

师：你注意到算式中有一个26吗？

生：注意到了。

师：观察算式中的26，你有什么发现？

生：没有变。

师：什么没有变？

生：26没有变。

师：26不变，它重要吗？

生：（停顿一下后说）重要，如果它变，和就不是这样变了（指着加3）。

师：你在右边写文字时，为什么不写26呢？

生：它没有变，就不用写了。

师：好的，你回答得很清楚，谢谢你。

从上述的访谈中可知，这个学生确实注意到了26这个不变量，但他认为在描述规律时，不需要写出不变量，只需将变化量表达出来即可。

实际上，这组算式的变化规律由两个等差数列的规律构成：第一个数列是有关第二个加数的数列，这个等差数列的通项公式为：第n行中的第二个加数=42+（n-1）×3。第二个数列是有关和的数列，这个等差数列的通项公式为：第n行的和=68+（n-1）×3。因此，第n行的算式可以表示为：26+［42+（n-1）×3］=68+（n-1）×3。（其中n=1，2，3，……）遗憾的是，没有学生在描述变量规律时，同时注意到行数，并表达出加数或和与行数之间的关系。

综上所述，本文通过对二、三年级学生解决“有规律加法算式问题”的表现进行测试与分析，揭示了学生在具体运算，归纳、运用一般化规律解决问题以及规律表达能力方面的测查结果。笔者将在后续文章《有规律加法算式问题的解决与早期代数思维培养的研究（下）》中，进一步针对这些测查结果探讨在小学数学教学中促进学生早期代数思维形成的具体策略。

参考文献：

［1］蔡金法.数学教育研究手册：上册［M］. 北京：人民教育出版社，2020.

［2］章勤琼，麦克斯·斯蒂芬斯.小学阶段“早期代数思维”的内涵及教学：墨尔本大学教授麦克斯·斯蒂芬斯访谈录［J］.小学教学（数学版），2016（11）：10-13.

［3］邓茜茜，丁锐.西方早期代数相关研究及启示［J］.小学教学（数学版），2023（5）：6-9.

［4］范德沃尔，卡普，贝-威廉姆斯.美国中小学数学教师实践手册：第10版［M］.张晶，侯慧颖，施银燕，等译.上海：华东师范大学出版社，2023.

［5］刘晓宇，朱红祥，于文华，等.早期代数思维在一～三年级的唤醒与渗透［J］.数学教育学报，2024，33（2）：34-40.