基于系统辨识的轴向磁悬浮轴承建模研究

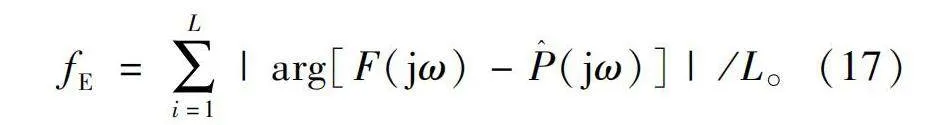
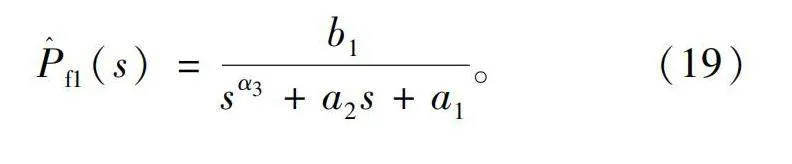
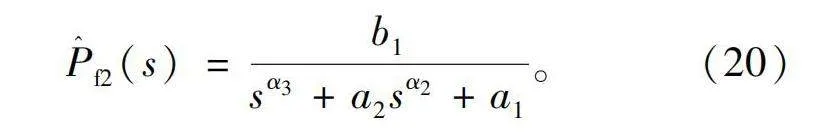
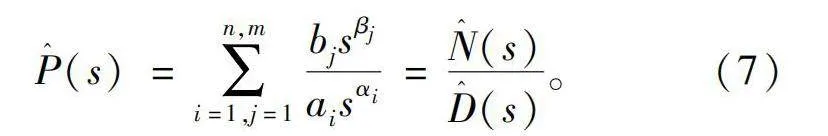
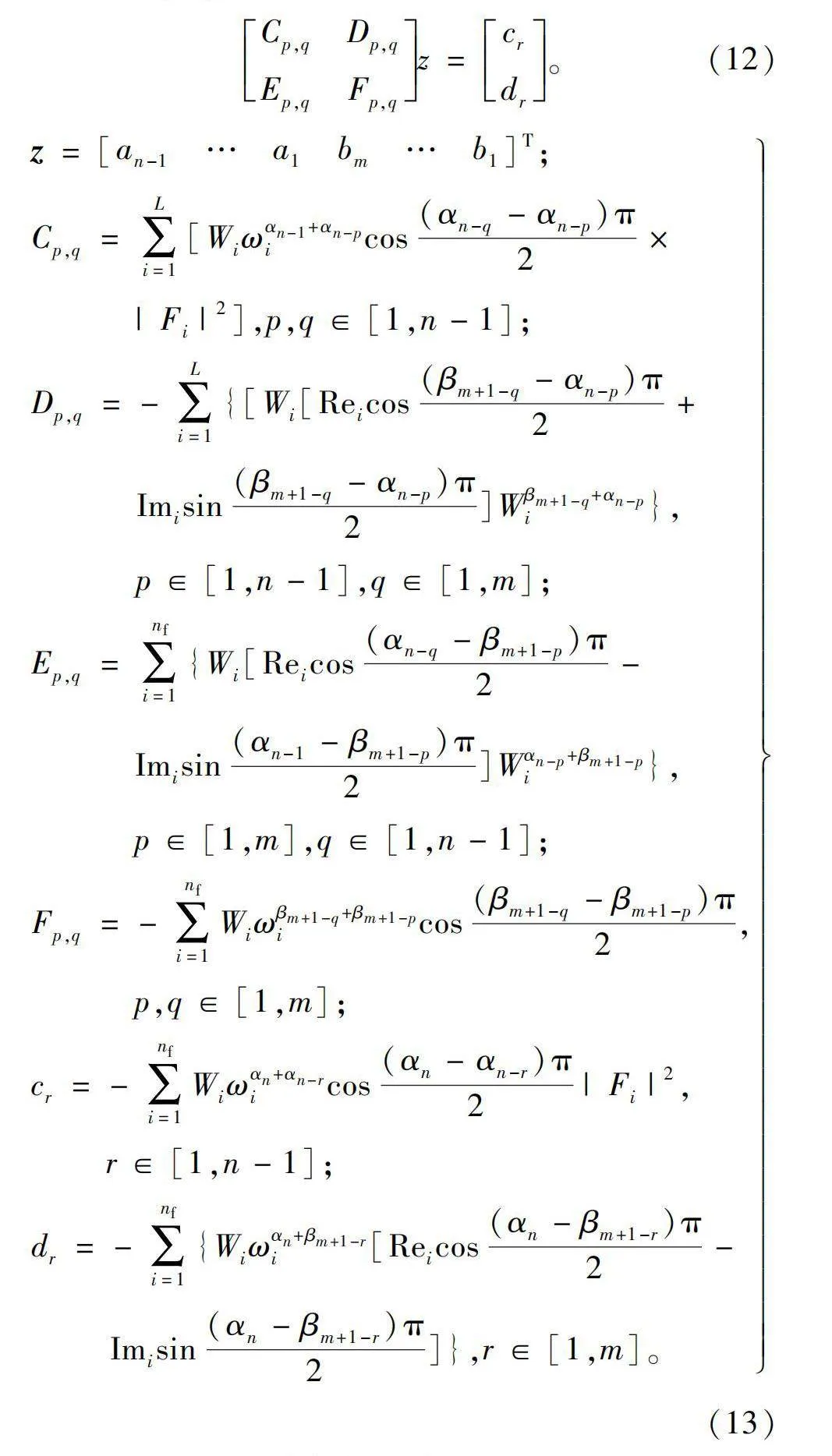
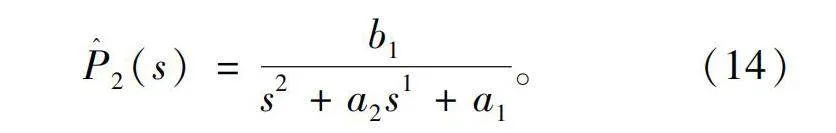
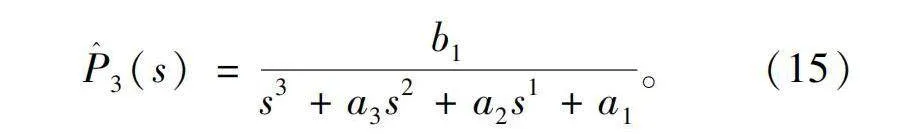
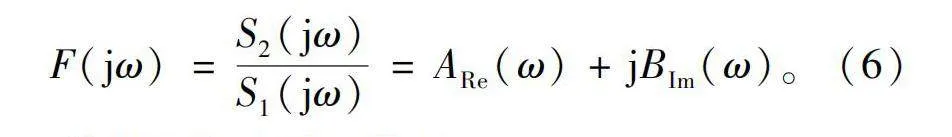
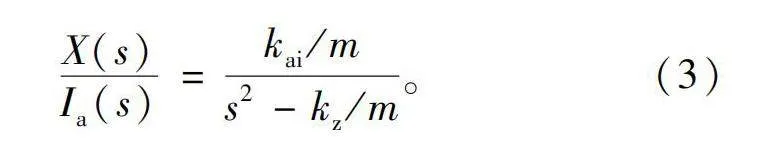
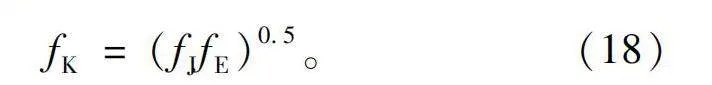
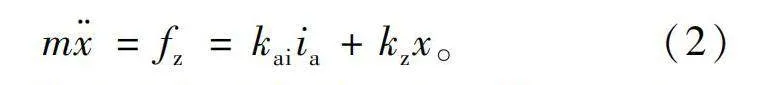
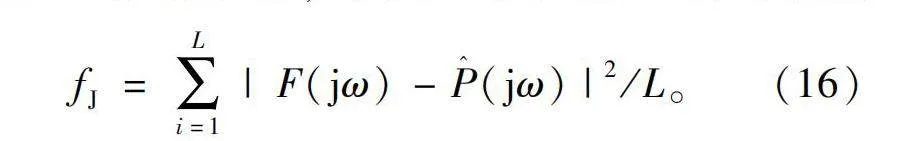
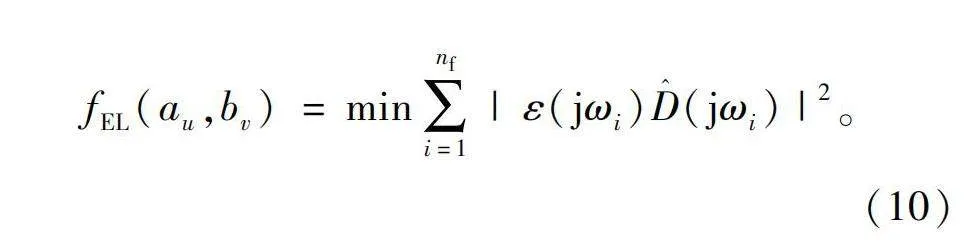
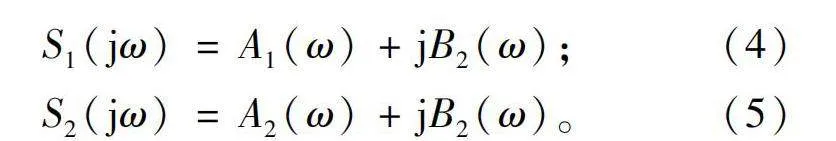
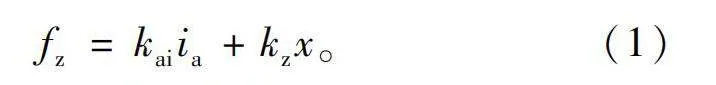
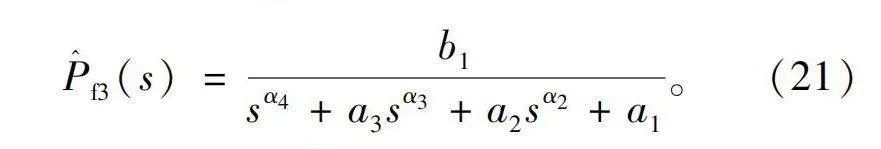
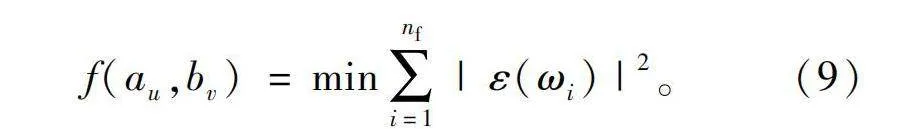
摘 要：磁悬浮轴承可有效地提升高速电机的临界转速，然而轴向磁悬浮轴承在转子高转速和材料实心的情况下涡流效应显著。针对该情况下实心轴向磁悬浮轴承的建模问题，使用等效磁路法建立轴向磁悬浮轴承模型时常会忽略涡流效应，导致理论模型与实际模型存在较大误差。为了得到更贴近实际的轴向磁悬浮轴承精确模型，针对一种混合型三自由度磁悬浮轴承的轴向部分采用系统辨识的方法进行了闭环辨识，研究了分数阶模型阶次的确定流程和误差准则，得到了轴向磁悬浮轴承的数学模型。结果表明，分数阶系统模型能够弥补整数阶模型在高频段上的相位特性误差，在整个频域上有着更高的精确度。

关键词：高速电机；磁悬浮轴承；三自由度混合型磁悬浮轴承；数学模型；系统辨识；分数阶系统

DOI：10.15938/j.emc.2024.10.008

中图分类号：TH133.3

文献标志码：A

文章编号：1007-449X（2024）10-0076-09

收稿日期： 2016-01-01

基金项目：

作者简介：宋学涛（1999—），男，硕士，研究方向为磁悬浮轴承建模及其控制；

邓智泉（1969—），男，博士，教授，博士生导师，研究方向为无轴承电机、高速电机、交流电机控制等。

通信作者：邓智泉

Research of modeling axial magnetic bearing based on system identification

SONG Xuetao， DENG Zhiquan

（College of Automation Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， China）

Abstract：Magnetic bearings can effectively increase the critical speed of high-speed motors，but axial magnetic bearings have a significant eddy current effect at high rotor speeds and solid materials. For the modeling of solid axial magnetic bearings， the eddy current effect is often ignored when using the equivalent magnetic circuit method to establish the axial magnetic bearing model， resulting in a large error between the theoretical model and the actual model. In order to obtain an accurate model of axial magnetic bearings closer to the reality， the axial part of a hybrid 3-degree-of-freedom magnetic bearing was identified， and the determination process and error criteria of the fractional order model were studied. The mathematical model of axial magnetic levitation bearing was derived. The results show that the fractional-order system model can compensate for the phase characteristic error of the integer-order model in the high frequency band， and has higher accuracy in the entire frequency domain.

Keywords：high-speed motors; magnetic bearings; hybrid 3-DOF magnetic bearing; mathematical model; system identification; fractional-order system

0 引 言

磁悬浮轴承相比机械轴承可以避免因摩擦而导致的寿命缩短、噪声大和转速限制等问题^［1］。目前磁悬浮轴承凭借其优良的特性，广泛应用在航空航天、医疗和高速透平机械等场合^［2-4］。磁悬浮轴承常使用实心材料作为其结构部件，在磁悬浮高速电机中，转子极高的转速对磁悬浮轴承的建模产生了许多影响，例如涡流效应、磁通饱和、气隙漏磁和边缘效应等会显著提升，影响着磁悬浮轴承的模型精确度，其中高速旋转下涡流效应的影响最为显著^［5］。研究者们在径向磁悬浮轴承的磁极和转子外层处使用叠片的结构，从而降低涡流效应^［6］。但该举措仅在径向磁悬浮轴承上具有良好的抑制效果，对于轴向磁悬浮轴承，由于其存在轴向上的磁通路径，故难以在轴向磁悬浮轴承中使用叠片的方式降低涡流效应。因此轴向磁悬浮轴承受涡流效应影响更为显著，影响着其建模准确性。

磁悬浮轴承的建模方法主要分为解析法和数值法，前者包含磁路法^［7］和子域模型法^［8］，后者主要是有限元法^［9］。目前较为成熟且运用广泛的解析方法是磁路法，它通过分析磁轴承的静态磁场得到气隙处的磁通量，最后通过磁共能的方式求得电磁力，经过线性化后得到磁悬浮轴承的数学模型。经过不断发展，该方法能够考虑的影响因素已十分丰富。例如，文献［10］中ZHU L等学者提出根据磁通分布划分区域，并找到了每个部件磁通路径与频率相关的磁阻，推导了考虑涡流效应的解析模型。文献［11］中对一种实心混合型轴向-径向磁悬浮轴承进行了考虑漏磁的磁路模型建模，得到了该结构的磁场分布和承载力。

然而上述方法中对于气隙和软磁材料的磁阻计算过程十分复杂。部分学者们提出从实验的角度出发，通过实验测量输入输出数据以获取模型的结构和参数，该方法称为系统辨识。传统磁路法中的电流刚度和位移刚度概念在控制中的成熟应用，学者们对系统辨识得到这两个参数的方法进行了大量研究。文献［12］中采用了两种不同的方法，即电磁力测量法和自由振荡法对磁轴承的两个刚度进行了参数辨识。文献［13］基于冲击响应的参数辨识方法，再结合冲击响应理论公式计算了磁轴承的支承参数。随着系统辨识计算的不断发展，研究者在模型结构及其参数的确定上进行了新的研究。文献［14］对一台实心同极性磁悬浮轴承的径向部分进行了闭环频域辨识，获得了与实际系统误差极小的模型。文献［15］对电压和电流驱动下的磁悬浮轴承进行了系统辨识，得出了涡流改变了电流驱动下模型阶次，修正了电压驱动下模型系数的结论，对于电流驱动下的辨识结果与实际系统仍存在较大误差。以上文献的辨识都是基于整数阶模型和径向磁悬浮轴承所得出的结果，然而对于涡流效应更为显著的轴向磁悬浮轴承建模和模型精确度提升的研究目前较少。

本文以一种轴向-径向混合型磁悬浮轴承为研究对象，首先介绍其基本结构、工作原理和实验平台。其次针对轴向部分磁轴承的模型建立，介绍闭环频域系统辨识建模方法的基本原理，模型结构组成和辨识算法，对混合型磁悬浮轴承的轴向部分进行系统辨识，并分析不同模型间的误差原因和特性。结果表明，对于轴向磁悬浮轴承，系统辨识模型与实验测量得到的系统误差较小，分数阶模型相较于整数阶模型具有更高的精确度。

1 混合型三自由度磁悬浮轴承结构与工作原理

1.1 混合型三自由度磁悬浮轴承的结构

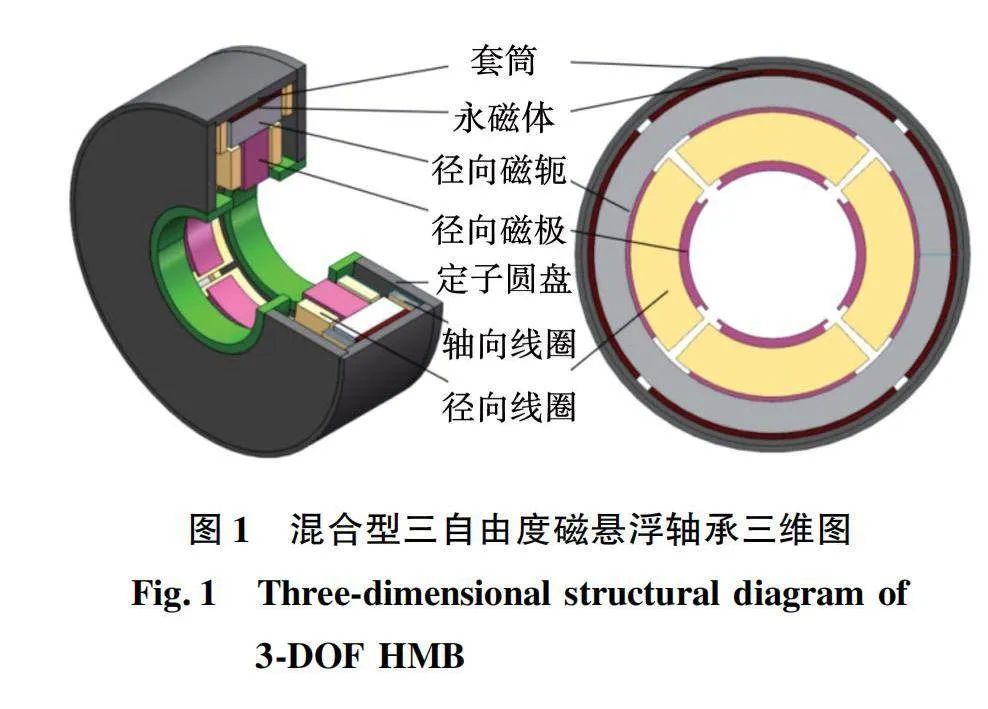
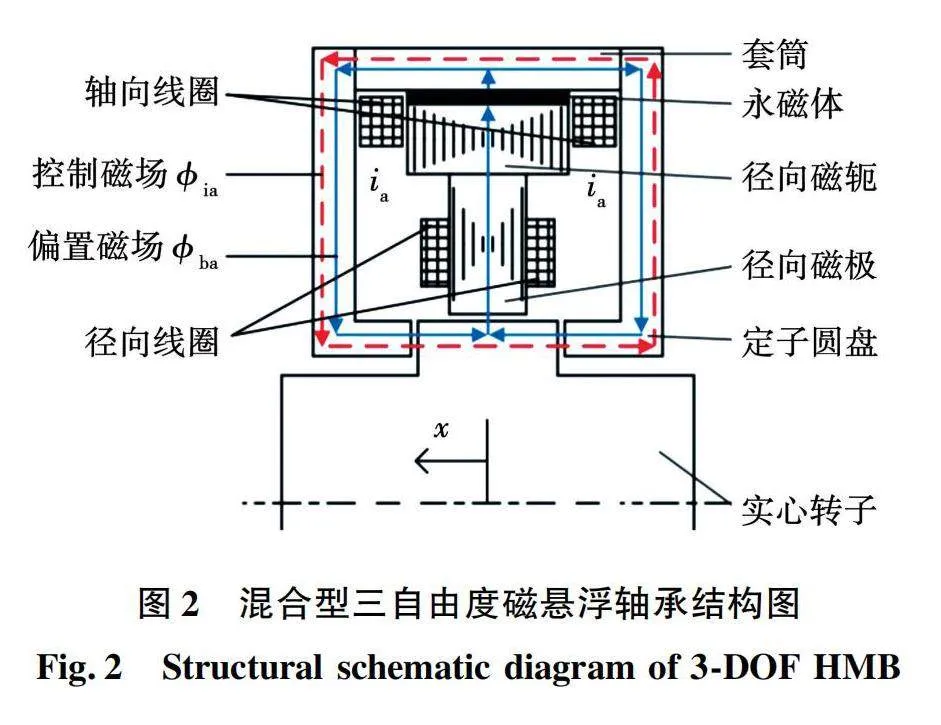
混合型轴向-径向三自由度永磁偏置磁轴承的结构图如图1所示，其具有结构紧凑、功率密度高的特性。它主要由定子套筒、永磁体、径向磁轭、径向磁极、定子圆盘、轴向线圈、径向线圈和实心转子组成。以结构功能划分，主要可以分为轴向和径向部分。其中径向部分的磁通由套筒内侧贴有的4片环状永磁体片产生，永磁体的剩磁特性提供持续的磁场偏置磁通。永磁体的充磁方向为平行充磁，永磁体环的N极朝向套筒内壁，S极朝向径向磁轭的外层；前后两个对称的定子圆盘与径向磁轭之间的内腔内设置轴向控制线圈，以通入可变电流产生可控的轴向控制磁场；4个相同的径向磁极周围缠绕有匝数确定的径向控制线圈，以提供可控的径向控制磁通，且径向磁极在径向上与转子的外壁之间留有气隙；

实验所研究的磁悬浮轴承实验平台由磁悬浮轴承和高速无刷电机共同组成，其中磁悬浮轴承部分使用两个混合型三自由度磁悬浮轴承，它们安装在高速永磁无刷直流电机两侧，使用同一根转轴将各个部分进行连接。

1.2 混合型三自由度磁悬浮轴承工作原理

对混合型三自由度磁悬浮轴承三维图进一步展开，得到如图2所示的详细结构图。该结构同时兼具径向和轴向两个方向上的磁场路径，现分别介绍偏置磁场和控制磁场的路径。偏置磁场的建立由贴附在套筒内侧的环状永磁体片产生，通过套筒从其两侧经过两个对称的定子圆盘，在经过前后两个轴向气隙进入到实心转子中，最后汇集经过径向气隙、径向磁极和径向磁轭后回到永磁体中，形成一个闭环的回路，其环路如图2中实线部分所示。而对于控制磁场主要分为轴向与径向两个磁场路径。轴向控制磁场由通入有电流的两个轴向线圈产生，其经过的路径为套筒、前定子圆盘、前轴向气隙、实心转子、后轴向气隙和后定子圆盘，其环路如图2中虚线部分所示。径向控制磁场由围绕在径向磁极周围通入有电流的径向线圈产生，其磁场路径与轴向控制磁场不在同一个平面内，主要经过上端径向磁极后分成两部分通过径向磁轭的轴向部分，最后在另一端汇集后再经过下端径向磁极、下端气隙、实心转子和上端气隙后形成环路。

由于径向磁悬浮轴承可以使用软磁材料叠片的方式大幅度降低涡流损耗，而轴向磁悬浮轴承无法使用该方式进行涡流损耗的降低，故主要分析混合型三自由度磁悬浮轴承的轴向部分。图2中可以看出轴向和径向控制磁场相互独立，轴向和径向的偏置磁场有所耦合，但是偏置磁场路径中存在着轴向和径向的独立气隙，在相应的气隙处的两个磁场叠加不受影响，故在分析该磁轴承时，可将径向和轴向独立进行分析，根据文献［16］中对工作点进行近似线性之后，磁力表达式可以写成

f_z=k_aii_a+k_zx。（1）

列写轴向磁轴承动力学方程

mx··=f_z=k_aii_a+k_zx。（2）

将其进行拉普拉斯变化，整理得到输入电流I_a与轴向磁轴承位移x之间的传递函数模型为

X（s）I_a（s）=k_ai/ms²－k_z/m。（3）

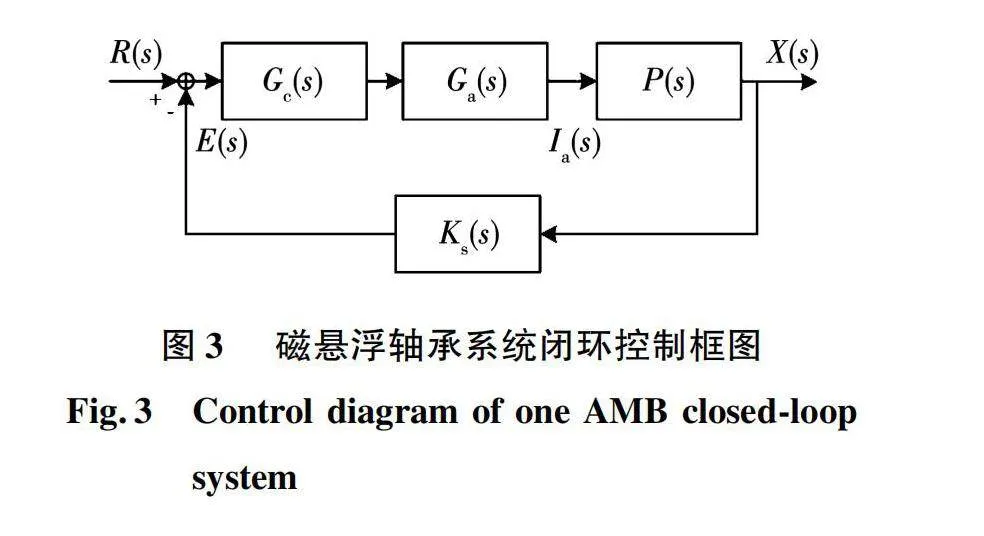
该模型为开环不稳定系统，需要选用合适的控制器，并通过极点配置法来调整控制器参数。实验中使用的控制器为工业中常用的PID控制器，其与磁悬浮轴承组成的闭环控制框图如图3所示。

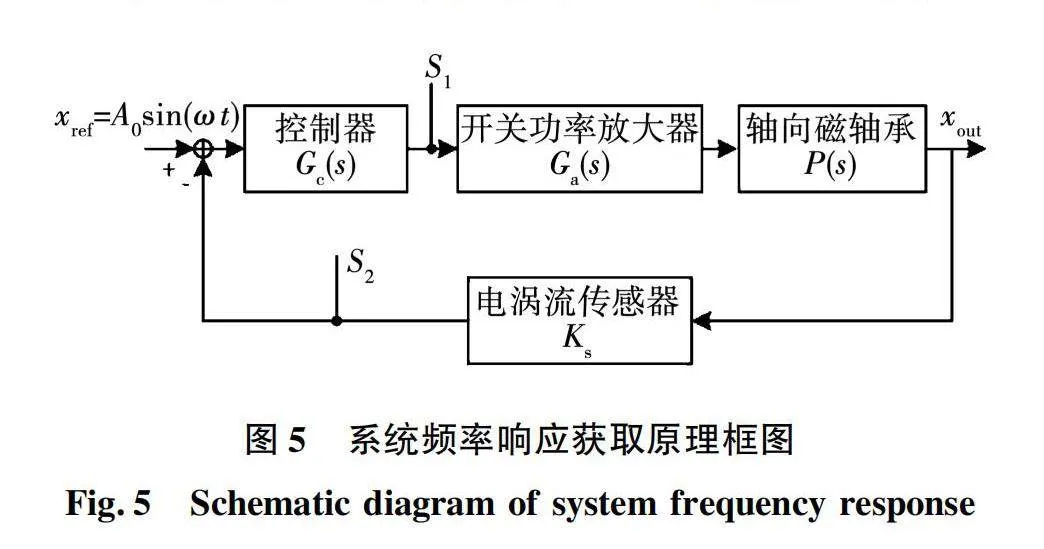
图3中：P（s）表示了磁悬浮轴承转子的动力学特性；K_s为电涡流位置传感器增益，其值有传感器的性能参数决定；G_c（s）表示PID控制器传递函数；G_a（s）表示开关功放传递函数，在理想的条件下，一般认为G_a（s）=1。

基于上述算法，搭建的磁悬浮轴承实验平台如图4所示，其主要由两个三自由度磁悬浮轴承、磁悬浮轴承控制器、开关功率放大器、位置传感器、直流电源和示波器组成。其中开关功率放大器采用三电平采样-保持控制算法，在工作频率范围内具有较好的跟踪精确度和线性度。位置传感器采用电涡流传感器，其灵敏度误差小于百分之三，非线性误差小于百分之一。

2 扫频和闭环辨识方法

2.1 频率扫描的基本原理

系统辨识的数据获取原理主要为频域响应辨识法。当磁悬浮轴承稳定地在平衡点附近工作时，在输入信号不影响稳定悬浮的情况下，可以将其视为线性系统。通过对磁悬浮轴承的输入端施加在工作频域范围内不同频率的正弦激励，并采集输入输出信号。对其进行离散傅里叶变换后得到对应频率下磁悬浮轴承闭环系统的幅值和相位信息。使用不同的模型结构进行拟合，得到模型结构下的最优传递函数。频率扫描的基本流程如下：

1）频率响应的获取。

磁悬浮轴承可以追踪参考位移。在正常工作的情况下，其参考位置给定为零。而为了对磁悬浮轴承进行频率扫描，将其输入更变为幅值为A₀，角频率为ω的正弦激励信号。在实验中，需要检测功率放大器输入信号S₁和电涡流位移传感器信号S₂。频率扫描的原理如图5所示，可看到，所获得的频率响应不仅包括磁悬浮轴承本体，还包括功率放大器和电涡流位移传感器，在正常工作的情况下，这两部分的传递函数可以等效为固定大小的增益环节。

正弦激励的初始幅值大致确定为磁悬浮轴承转子最大位移的8%，然后按照能够保持系统在较高频率时稳定的要求进行适当减小。激励的频率ω选取了10～500 Hz内的一系列频率，并按照固定的比例进行变化。并且为了使得采样时长为信号周期的整数倍，需要对频率进行修正，这样能够在不使用窗函数的情况下，减小计算量同时得到准确的结果。

2）输入与输出信号的采集。

实验中采用示波器对信号S₁和S₂进行采集，示波器的采样频率为兆赫兹级，远高于磁悬浮轴承的工作频率范围，故可以忽略由采样造成的延时误差。所得到的数据为离散的时域序列，需要进一步的采用计算机进行离散傅里叶变换，以得到磁悬浮轴承在该频率范围下信号的幅值与相位信息。

假设经过离散傅里叶变换后得到的频率响应信息分别为S₁（jω）和S₂（jω），令

S₁（jω）=A₁（ω）+jB₂（ω）； （4）

S₂（jω）=A₂（ω）+jB₂（ω）。（5）

将得到的输入输出响应进行处理，磁悬浮轴承系统的频率响应即可表示为

F（jω）=S₂（jω）S₁（jω）=A_Re（ω）+jB_Im（ω）。（6）

2.2 模型结构及辨识算法

模型结构的选取是系统辨识的前提，实验得到频率响应数据需要选择合理的模型结构，之后再计算得到系统最优模型。传递函数的一般形式可以用如下的结构进行表示：

P^（s）=∑n，mi=1，j=1b_js^β_ja_is^α_i=N^（s）D^（s）。（7）

式中，为保持传递函数的统一性，令a_n=1。对实验数据和拟合模型进行作差，且定义为ε（ω），其表达式为

ε（ω）=A_Re（v）+jB_Im（ω）－N^（jω）D^（jω）。（8）

式（7）的系数求解问题可以转化为多系数函数的最小二乘法求极值问题，即

f（a_u，b_v）=min∑n_fi=1|ε（ω_i）|²。（9）

式中u=0，1，…，m；v=0，1，…，n；n_f表示实验数据中频率响应的个数。

然而直接对该式求导，所得到的方程为非线性方程，求解较为复杂。为使得问题简化，将误差乘上模型的分母^［17］，这样转化后的最小二乘极值问题可以用如下式表示：

f_EL（a_u，b_v）=min∑n_fi=1|ε（jω_i）D^（jω_i）|²。（10）

由于不同频率处的分母不同，会使得拟合模型的误差增加，因此对不同频率处的分母引入加权系数以减小这种误差^［18］。加权系数W（ω_i）的迭代计算公式如下，其中h表示目前迭代的次数。在迭代中令初始迭代中的W₁（ω_i）均为1。

至此利用式（11）中的迭代计算公式分别对未知系数a_u，b_v进行求导，获得线性矩阵方程如下：

C_p，qD_p，q

矩阵中各系数的详细表达式（13）所示，c_r和d_r为常数。为了公式表达简洁，将|F（jω_i）|简写成|F_i|，其他例如Re_i、Im_i和W_i分别是频率为ω_i时的实验频率响应的实部、虚部和分母加权系数。每次迭代中进行该方程的求解，在迭代误差小于给定值时终止计算，即可得到对应误差最小二乘极值的一组最优模型系数。

3 扫频结果的拟合分析

本节首先使用整数阶的模型结构对模型中的参数进行求解，在1.2节中确定了理论模型的阶次为2，相位为固定值-180°，然而通过实验获取到频率响应的相位滞后超过-180°，故需要对理论模型进行增加阶次等修改措施以拟合实验数据。文献［19］提出，实心磁悬浮轴承由于涡流效应的影响，会使得系统呈现分数阶的特性，仅提高整数阶模型的阶次对拟合精确度的提升有限，故进一步地使用了分数阶模型结构进行拟合，以提高系统模型的精确度。最后对两种模型结构的拟合效果进行了综合分析。

3.1 整数阶模型结构拟合

首先对理论模型中的分母添加一次项，使其相位特性能够满足，此时的模型结构为

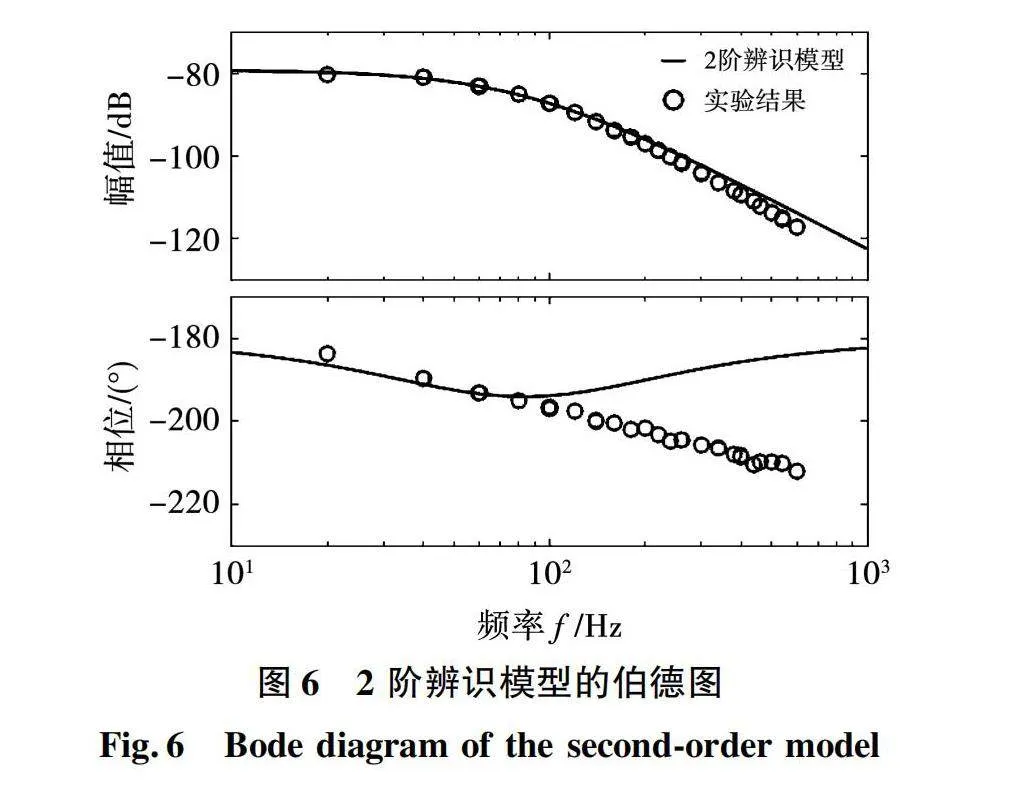
对该模型结构使用2.2节中的辨识算法，可以得到在满足设定迭代误差下的模型参数，具体为b₁=29.69，a₂=-265.31，a₁=-276 529.47。

将该模型结构下的最优模型与实验频率响应绘制在同一伯德图中，结果如图6所示。从图中可以看出采用分母添加一次项之后的二阶模型在工作频域内的幅值特性有着较好的精确度，但在相位上有着较大的误差，且在频域的后半段与实际系统在相位上滞后的更多，误差不断增大。

为提升辨识模型的精确度，将模型结构的阶次提升至3阶，此时其表达式为

P^₃（s）=b₁s³+a₃s²+a₂s¹+a₁。（15）

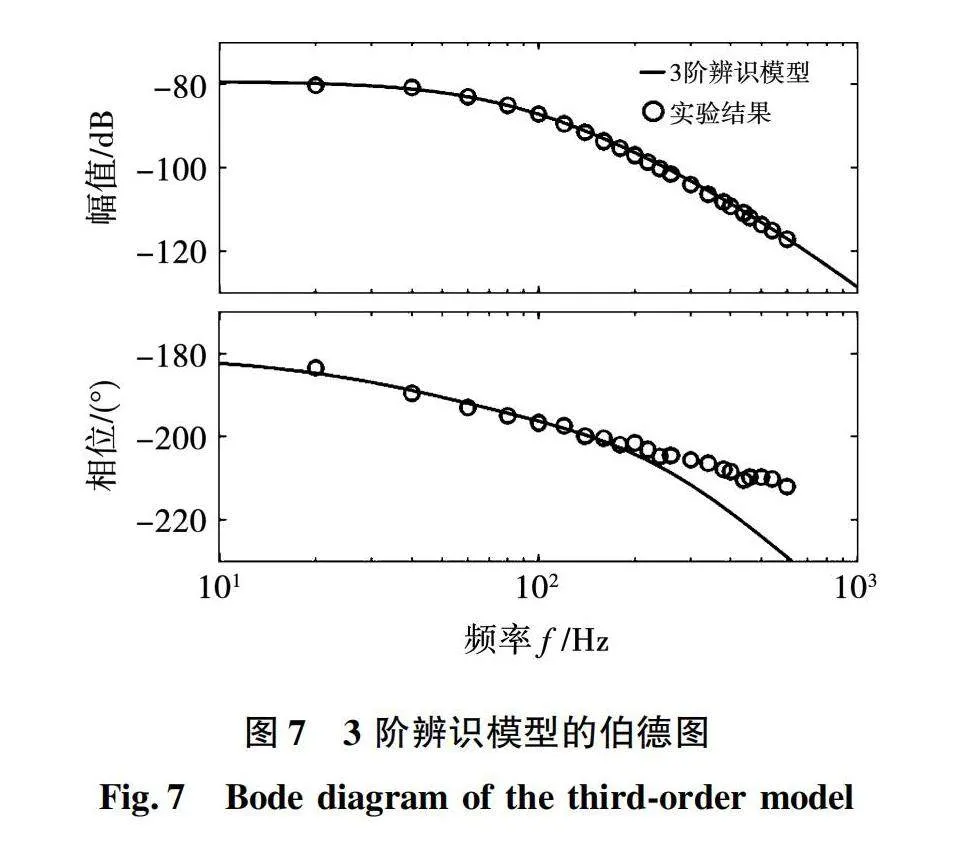
计算后得到模型中的参数为b₁=10 401.17，a₃=3 375.76，a₂=-684 713.32，a₁=-974 712 530.29。其最优模型的伯德图如图7所示。

与二阶辨识模型相比，三阶辨识模型在幅值特性和相位特性上都能够更好地描述实际系统，然而在高频段上相位的描述还是不够准确，即100 Hz左右开始出现辨识模型的相位滞后超过实际系统的现象。当整数阶拟合模型的阶数继续提升时，所得到模型精确度的提升十分有限，通过提升整数阶拟合模型的阶数无法获得精确度更为理想的模型。文献［19］通过理论推导得出了模型结构应该位于2至3阶之间。因此，为了能够更加准确地描述实际系统，采用分数阶模型结构进行系统辨识。

3.2 分数阶模型结构拟合

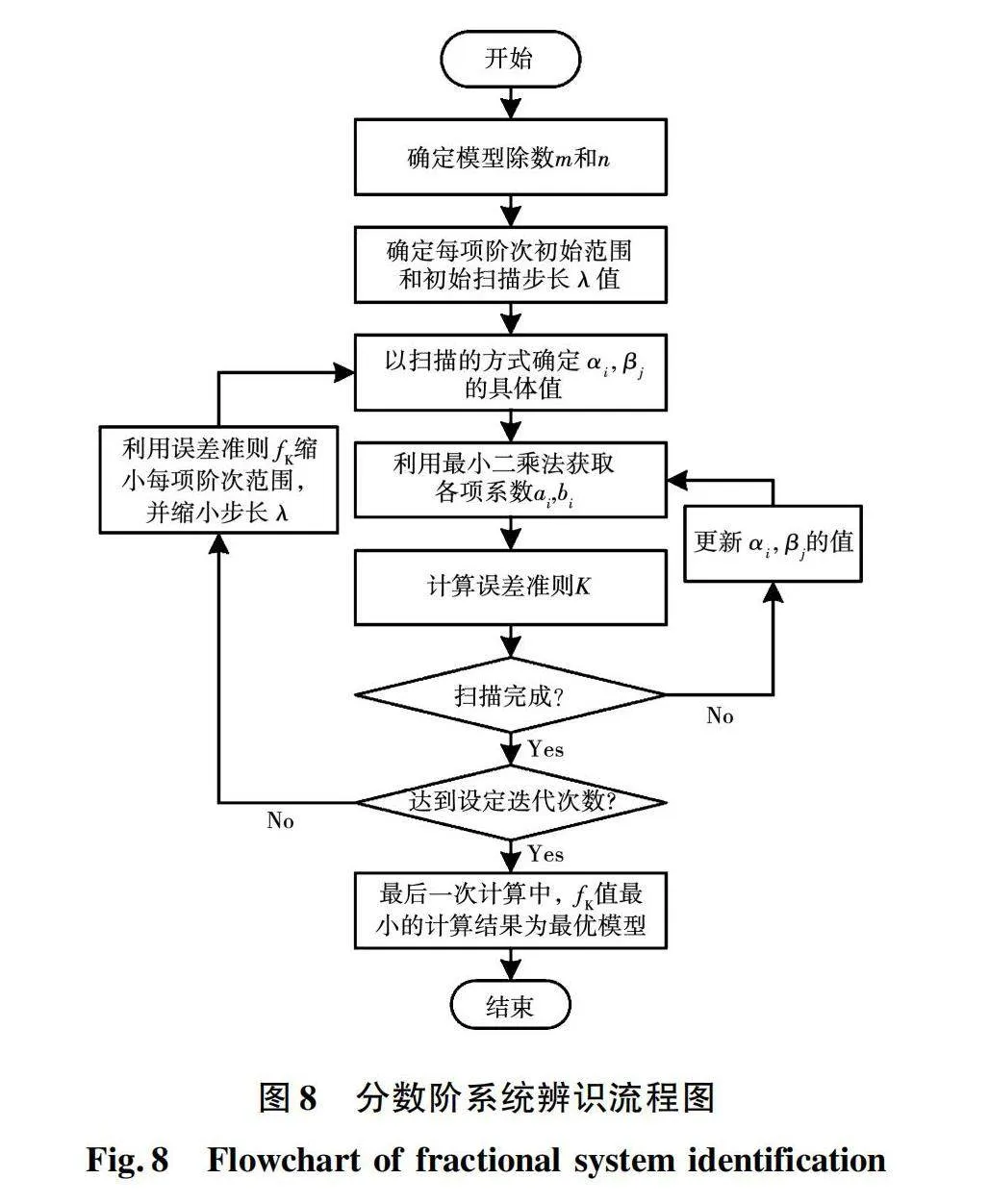
分数阶模型指式（7）中的α_n不在是整数，而是处于两个整数之间的分数形式。由于分数阶模型参数并没有明确的物理意义，模型结构的阶次较难直接确定。模型结构的确定主要有两个部分，一是模型项数的确定，二是模型阶次的确定，即式中m和n的取值，和每项中α_i的确定。

首先是模型项数的确定，由图6中的对比结果可知，实际系统是一个2阶以上的系统，故在模型项数的确定上，根据模型误差的变化趋势依次增加分数阶项数的个数。其次是模型阶次的确定，使用扫描的方法以缩小模型阶次的范围，并按照从高阶次到低阶次的顺序确定每项的阶数值，即先确定分母最高阶次α_n，再按照0lt;α₂lt;α₃lt;…lt;α_n条件约束依次取值，该过程流程如图8所示。

对于误差准则的选取，使用较多的准则是均方差准则，即式（16）所示。从该式中可以看出该准则仅考虑了模型的幅值，而对于相位是没有考虑到的。

f_J=∑Li=1|F（jω）－P^（jω）|²/L。（16）

为解决整数阶模型存在的相位误差，引入一个辅助准则，从而使得相位误差也可以纳入到算法的考虑范围之中。

f_E=∑Li=1|arg［F（jω）－P^（jω）］|/L。（17）

将上述的两种误差准则取几何平均值f_K，如式（18）所示，将其作为分数阶系统辨识的最终准则，当两种误差准则都达到最小值时，即f_K最小时所得到的模型为最优模型。

f_K=（f_Jf_E）^0.5。（18）

根据分数阶的模型结构按照项数逐渐增加的形式提出以下3类模型，现对3种模型结构及拟合结果进行详细说明：

1）模型结构P_f1。

P^_f1（s）=b₁s^α₃+a₂s+a₁。（19）

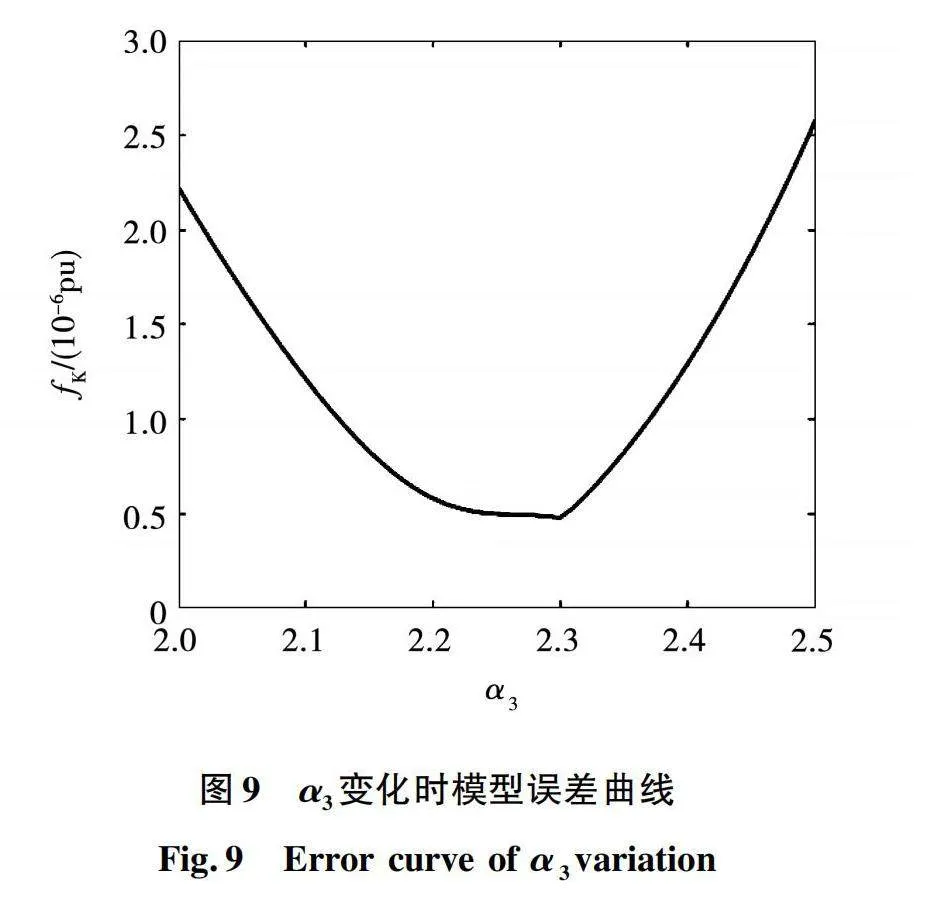
从整数阶辨识结果中判断，α₃所在的范围为［2，3］，在该范围内使用分数阶系统辨识扫描算法得出该范围模型下的误差f_K随模型阶次α₃的变化曲线如图9所示。

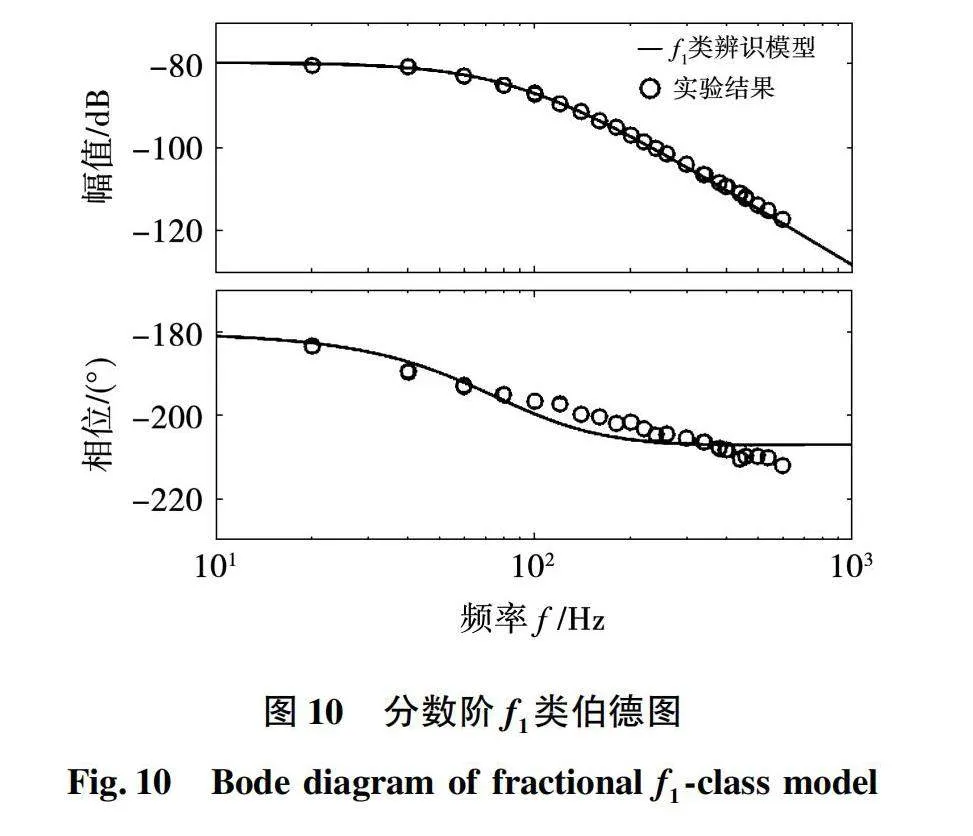
从图9中可以得到一个较小的范围区间即2.2～2.3，以此类推，缩小步长对该区间进一步的扫描。当达到设定的迭代次数时，停止计算，得出系统在该模型结构下的最优模型参数为α₂=2.30，b₁=206.26，a₂=-597.87，a₁=-2 030 172.51。f₁结构最优模型的伯德图如图10所示。

由图10中可以看出采用f₁模型结构时，两者在幅值上的误差较小，在相位上仍存在较大的误差，但与2阶模型相比，其相位在高频段时，能够更好地描述实际系统。其原因是与2阶辨识系统相比，f₁模型结构的阶次更高，描述系统的变量更多。但f₁只采用了一个未知阶次变量α₃，并不能在整个频域内保持较好的相位误差，故进一步添加未知阶次变量，即f₂模型结构。

2）模型结构P_f2。

P^_f2（s）=b₁s^α₃+a₂s^α₂+a₁。（20）

对于该模型扫描的基本步骤为先确定α₃的值，再确定α₂的值。设定α₃的初始范围仍然为［2，3］，其初始扫描的步长设为0.1，然后在每个确定的α₃下对α₂进行扫描计算，为了尽可能地包含各个阶次组合，选取α₂的范围为［0.1，α₃-λ］。当第一次扫描完成后，根据误差f_K确定一个比初始范围小的范围区间，将这个新的范围区间作为α₃的范围并缩小步长再一次进行扫描计算，直到达到设定的迭代次数。取最后一次计算中的误差f_K最小时对应的α₃作为该结构模型的最优参数。当确定了α₃的系数后，采用1）中的算法对α₂进行迭代计算，获取最优参数。

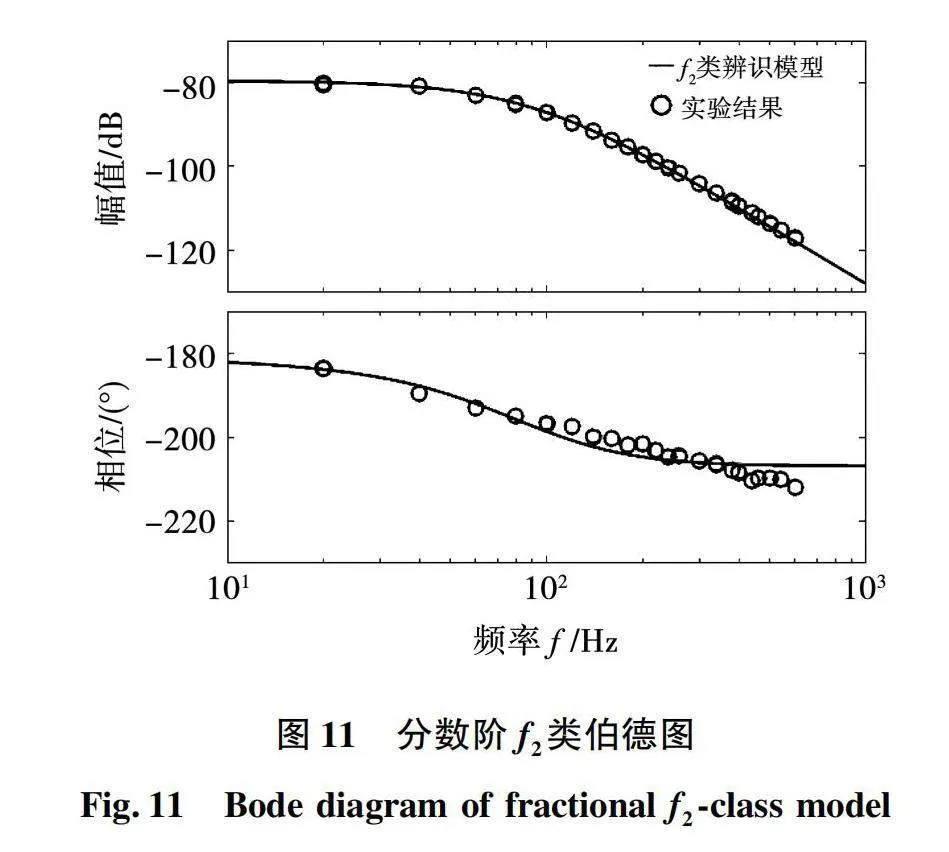
通过迭代的方式最终计算得到在f₂模型结构下的最优模型参数为α₃=2.30，α₂=0.66，b₁=215.08，a₂=-5 750.94，a₁=-2 028 527.03。f₂最优模型的伯德图如图11所示。

由图11中可以看出，f₂模型结构在幅值和相位的描述上相对于f₁模型结构在拟合精确度上都有一定程度的提升。从结果上来看，提高分数阶模型的阶次项可以增加模型在整个频域上的拟合精确度；与整数阶模型中的3阶模型相比，其相位特性不仅在低频段上能够被较好地描述，在高频段上也能够保持一定的精确度。然而，对于更高频域的相位描述，该模型结构呈现误差逐渐增大的趋势。因此，为了消除该趋势并提升模型精确度，进一步增加项数。

3）模型结构P_f3。

P^_f3（s）=b₁s^α₄+a₃s^α₃+a₂s^α₂+a₁。（21）

该模型结构的参数算法与2）中的类似，即α₄、α₃和α₂依次确定。扫描中α₄的初始范围设置为［2，3］，并按照α₄gt;α₃gt;α₂的约束进行迭代计算。

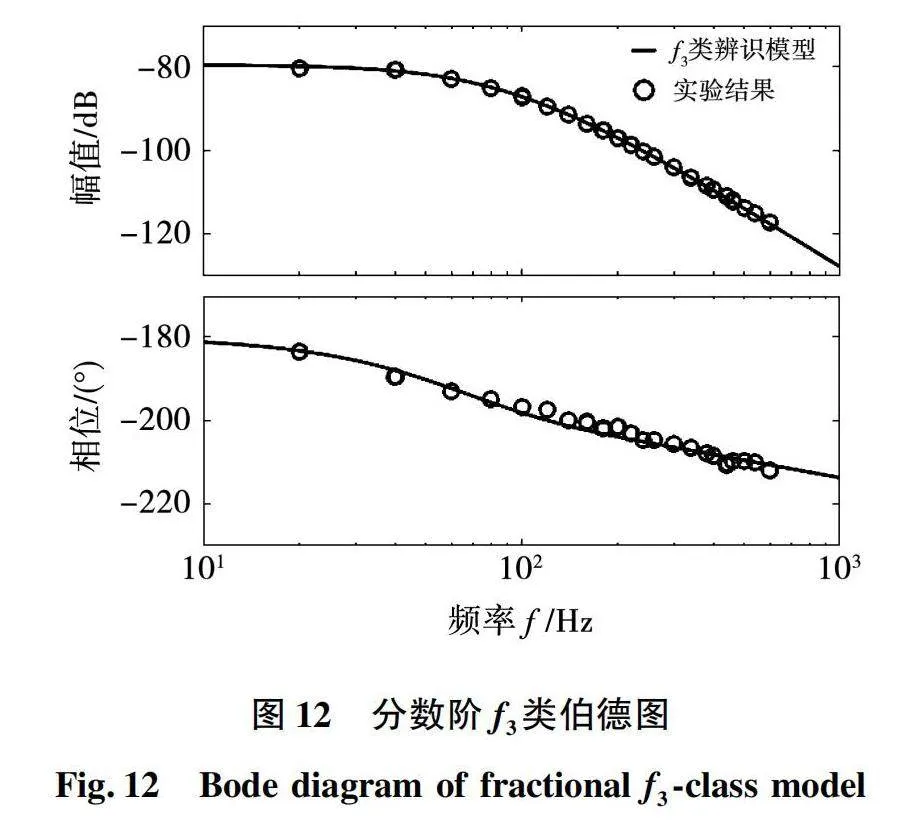
最终通过计算得到在f₂模型结构下的最优模型参数为α₄=2.50，α₃=1.63，α₂=1.52，b₁=1 499.30，a₃=1 545.09，a₂=-2 856.97，a₁=-14 640 476.76。f₂结构最优模型的伯德图如图12所示。

模型结构f₃能够达到较高的一致性，与f₂类辨识模型相比无论是在幅值还是在相位上都有着更高的精确度，能够很好地描述实际系统。理论上可以通过再增加分数阶模型的项数以提高模型的整体精确度，但是过于复杂的模型对于控制器和算法设计上没有意义。

3.3 辨识结果分析

综合系统辨识结果可以看出，磁路法理论推导出的2阶模型无法准确地描述实际系统。这种情况的原因是在磁悬浮轴承在实际运行过程中，为应对转子旋转带来的不平衡振动等因素，线圈中的控制电流通常不是一个稳定的直流，而是幅值和频率存在变化的电流。在磁路模型的建立中忽略的涡流、磁滞、磁饱和、漏磁、边缘效应和过盈装配等因素会被放大，从而导致系统出现幅值和相位的改变，这种现象在采用实心材料的轴向磁悬浮轴承中更为明显。

从两种模型结构的拟合结果中可以看出，随着模型中项数不断增加，拟合精确度也随之增加。该现象的原因是分母项数增加使得系统模型描述整个频域的自由度增多，使得系统模型能够在各频段下准确地描述系统特性，从而达到较高的精确度。在综合两种类别的结果后，可以发现整数阶系统在中低频段时，幅值特性的描述已经能够达到一定的精确度，但相位特性的描述还存在一定的误差。分数阶的模型结构能够弥补整数阶模型在相位特性描述上的问题，使得模型的精确度进一步提高。但是其系统模型结构也更为复杂。对于选择合适的模型进行控制器的设计也是一个值得研究的问题，然而分数阶模型在整数阶模型无法继续提高精确度的情况下，为更加精确的模型建立提供了另一种方式，这对设计高性能控制和接近更加真实情况下的仿真提供了参考。

4 结 论

本文针对由于实心轴向磁悬浮轴承涡流效应显著而带来的建模问题，采用了闭环频域系统辨识的方法对一种混合型磁悬浮轴承的轴向部分进行了建模。由于整数阶模型难以准确描述系统相位特性，在整数阶模型辨识算法的基础上进一步研究了分数阶模型辨识算法，对其误差准则和辨识流程进行了定义和阐述。结果表明，整数阶模型对于系统幅值特性描述较好，而相位特性存在较大误差。分数阶模型相较于整数阶在相同的项数下有着更高的幅值和相位精确度。

参 考 文 献：

［1］张维煜， 朱熀秋， 袁野. 磁悬浮轴承应用发展及关键技术综述［J］. 电工技术学报， 2015， 30（12）： 12.

ZHANG Weiyu， ZHU Huangqiu， YUAN Ye. Study on key technologies and applications of magnetic bearings［J］. Transactions of China Electrotechnical Society， 2015， 30（12）： 12.

［2］刘彬， 房建成， 刘刚. 一种磁悬浮陀螺飞轮方案设计与关键技术分析［J］. 航空学报， 2011， 32（8）： 1478. LIU Bing， FANG Jianchen， LIU Gang. Design of a magnetically suspended gyrowheel and analysis of key technologies［J］. Chinese Journal of Aeronautics， 2011， 32（8）： 1478.

［3］李红伟， 范友鹏， 张云鹏， 等. 轴流式人工心脏泵混合磁悬浮系统的耦合特性［J］. 电机与控制学报， 2014， 18（5）： 105.LI Hongwei， FAN Youpeng， ZHANG Yunpeng， et al. Coupling in hybrid magnetic levitation system of axial-flow blood pump［J］. Electric Machines and Control， 2014， 18（5）： 105.

［4］刘程子. 适用于高速电机的混合型磁悬浮轴承设计及控制策略的研究［D］. 南京航空航天大学， 2015.

［5］岩桦， 虞烈. 实心转子电磁轴承涡流损耗分析［J］. 中国电机工程学报， 2002， 24（2）： 117.

SUN Yanhua， YU Lie. Eddy current loss analysis in radial magnetic bearings with solid rotor［J］. Proceedings of the CSEE， 2002， 24（2）： 117.

［6］吴帆. 硅钢片的各向异性对磁悬浮轴承磁性能的影响研究［D］. 南京航空航天大学， 2018.

［7］梅磊， 邓智泉， 赵旭升等. 新结构混合型径向磁悬浮轴承［J］. 电工技术学报， 2009， 24（5）： 13. MEI Lei， DENG Zhiquan， ZHAO Xusheng，et al. New configuration hybrid radial magnetic bearing［J］. Transactions of China Electrotechnical Society， 2009， 24（5）： 13.

［8］YU Chunming， DENG Zhiquan， CHEN Shangsi， et al. A novel subdomain and magnetic circuit modeling method for hybrid homopolar radial magnetic bearings［J］. Mechanical Systems and Signal Processing， 2022， 170： 108823.

［9］孙玉坤， 吴建兵， 项倩雯. 基于有限元法的磁悬浮开关磁阻电机数学模型［J］. 中国电机工程学报， 2007， 7（12）： 33.

SUN Yukun， WU Jianbing， XIANG Qinman. The mathematic model of bearingless switched reluctance motor based on the finite-element analysis［J］.Proceedings of the CSEE，2007，7（12）： 33.

［10］ZHU L， KNOSPE C R， MASLEN E H. Analytic model for a nonlaminated cylindrical magnetic actuator including eddy currents［J］. IEEE Transactions on Magnetics，2005，41（4）：1248.

［11］禹春敏， 邓智泉， 梅磊， 等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究［J］. 电工技术学报， 2021， 36（6）： 1219. YU Chunming， DENG Zhiquan， MEI Lei， et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit［J］. Transactions of China Electrotechnical Society， 2020， 36（6）： 1219.

［12］白金刚， 张小章， 张剀， 等. 磁悬浮储能飞轮系统中的磁轴承参数辨识［J］. 清华大学学报， 2008， 11（3）： 382.

BAI Jinggang， ZHANG Xiaozhang， ZHANG Kai， et al. Parameter identification for active magnetic bearings in energy storage flywheel［J］.Journal of Tsinghua University，2008，11（3）：382.

［13］施建， 李黎川. 磁悬浮系统动力学参数的开环辨识［J］. 微细加工技术， 2004， 15（2）： 72.

SHI Jian， LI Lichuan. Open-loop identification of dynamics parameters of magnetic suspended system［J］. Microfabrication Technology， 2004， 15（2）： 72.

［14］钟建朋， 李黎川. 实心磁路磁轴承的分数阶系统辨识［J］. 中国电机工程学报， 2013， 33（18）： 170. ZHONG Jianpeng， LI Lichuan. Fractional-order system identification of a solid-core active magnetic bearing［J］. Proceedings of the CSEE， 2013， 33（18）： 170.

［15］周亮， 李黎川. 电流驱动和电压驱动下实心磁路磁轴承的系统辨识［J］. 中国电机工程学报， 2016， 36（1）： 268. ZHOU Liang， LI Lichuan. System identification of solid-core active magnetic bearings under current drive and voltage drive［J］. Proceedings of the CSEE， 2016， 36（1）： 268.

［16］GERHARD S， ERIC H M，等. 磁悬浮轴承： 理论、设计及旋转机械应用［M］. 徐旸， 张剀， 赵雷， 译. 北京： 机械工业出版社， 2012.

［17］LEVY E. Complex curve fitting［J］. IRE Transactions on Automatic Control， 1959， 4（3）： 37.

［18］SANATHANAN C， KOERNER J. Transfer function synthesis as a ratio of two complex polynomials［J］. IEEE Transactions on Automatic Control， 1963， 8（1）： 56.

［19］ZHU L， KNOSPE C R. Modeling of nonlaminated electromagnetic suspension systems［J］. IEEE/ASME Transactions on Mechatronics， 2009， 15（1）： 59.

（编辑：刘素菊）