基于预设时间一致性的虚拟同步发电机二次电压控制
2024-12-03李斌龚祥祥胡丹丹曾志辉王浩

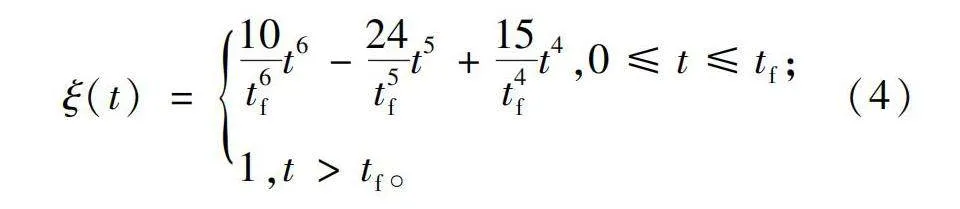
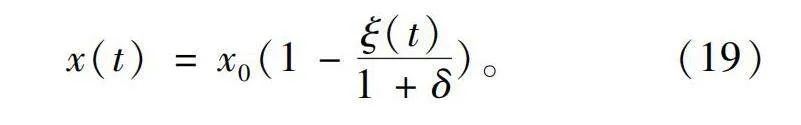
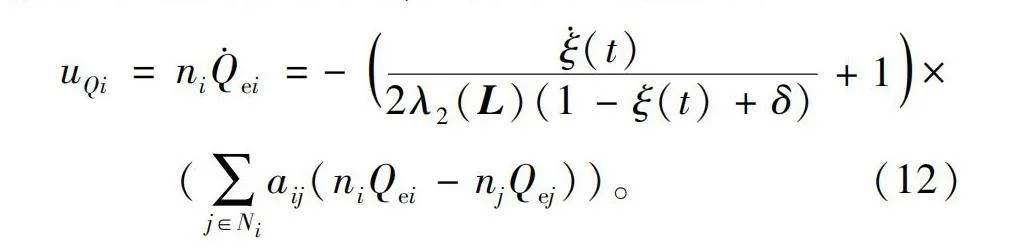
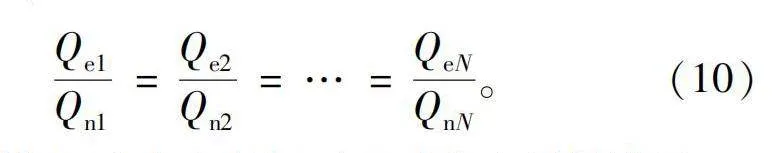
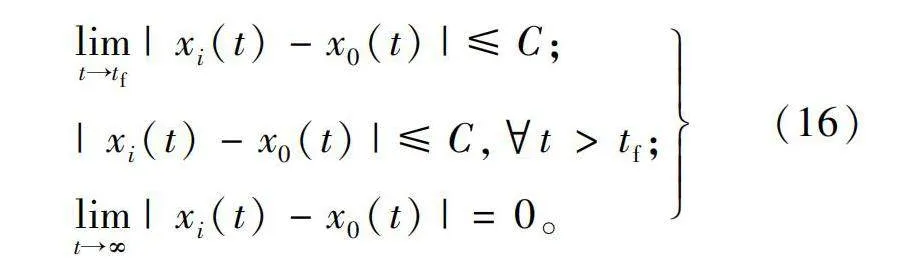
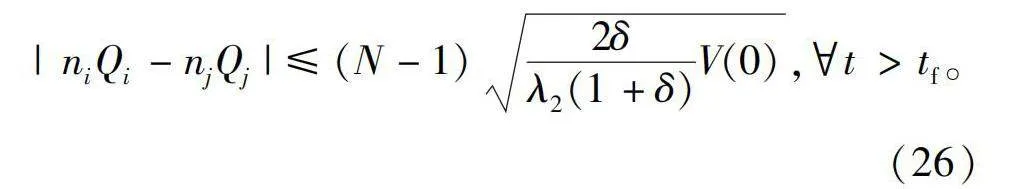
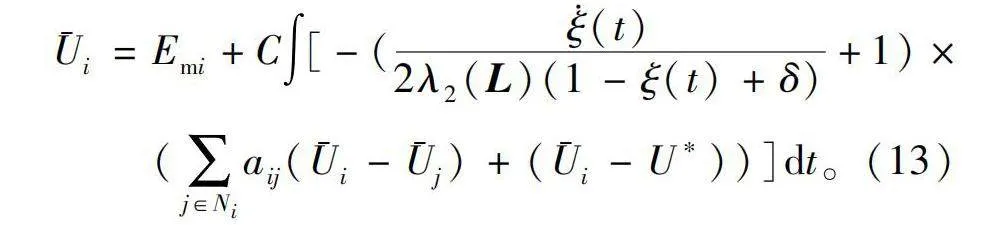
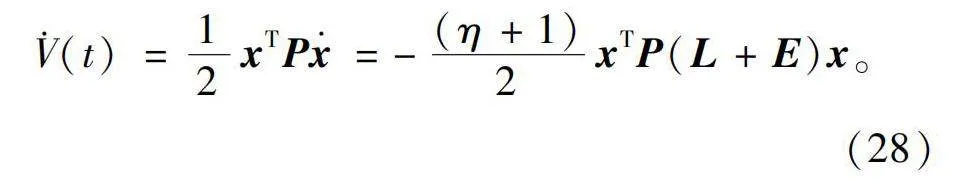
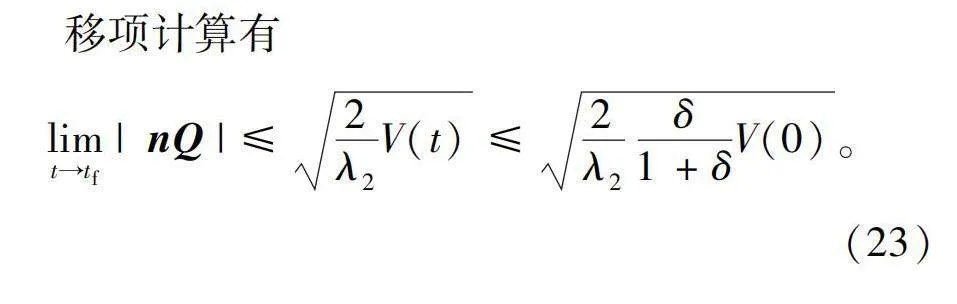
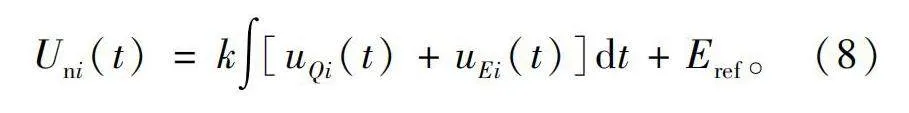
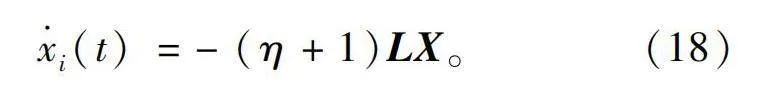
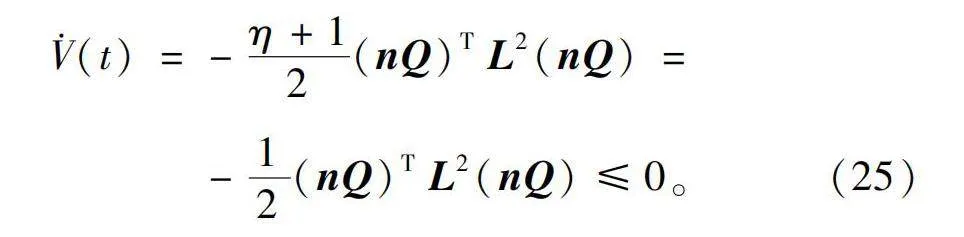
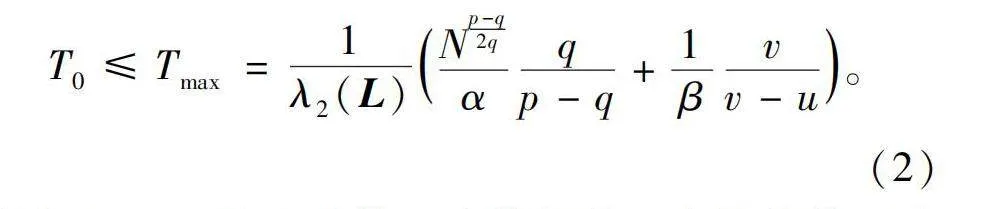
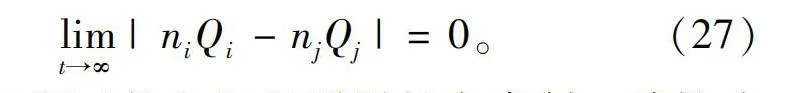
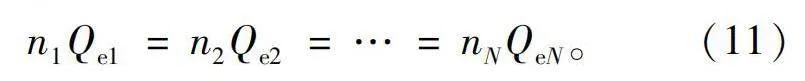
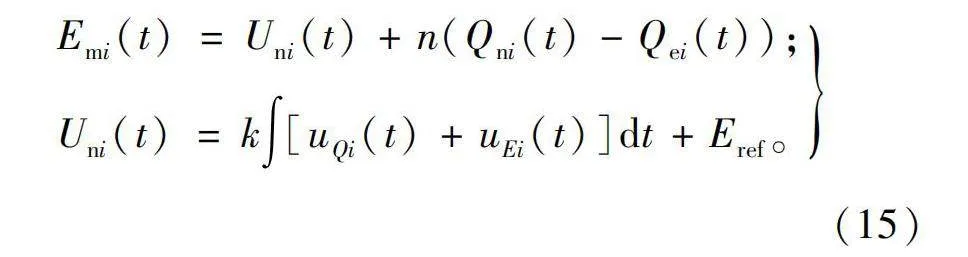
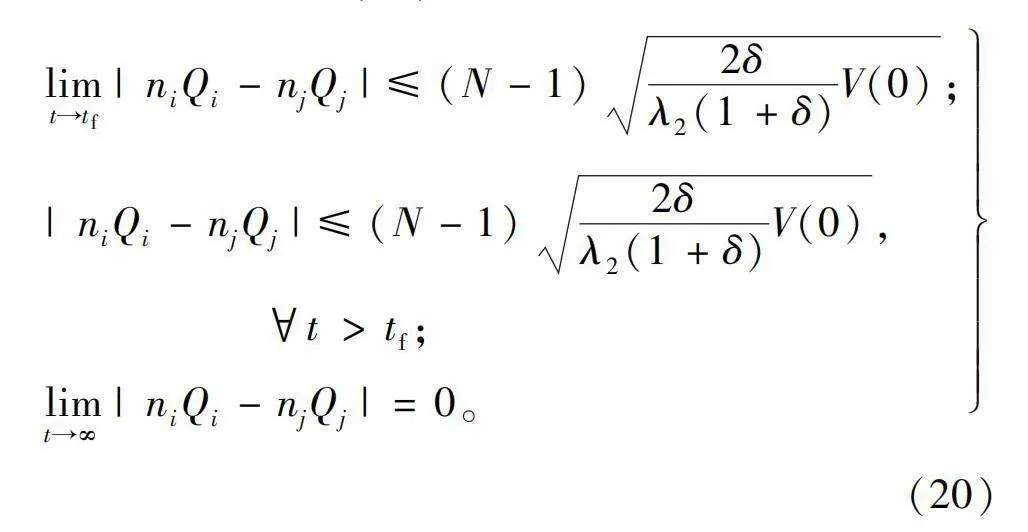
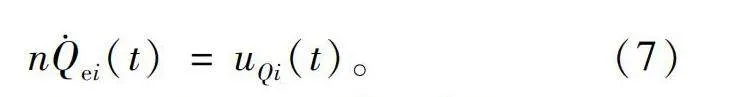
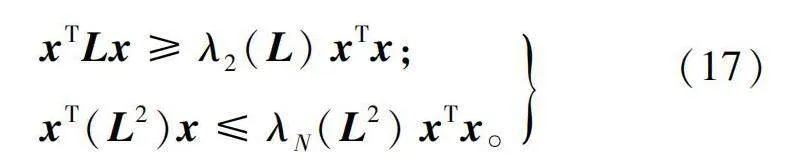
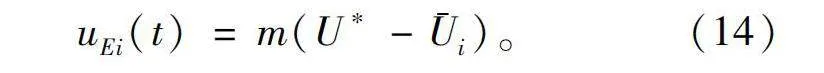

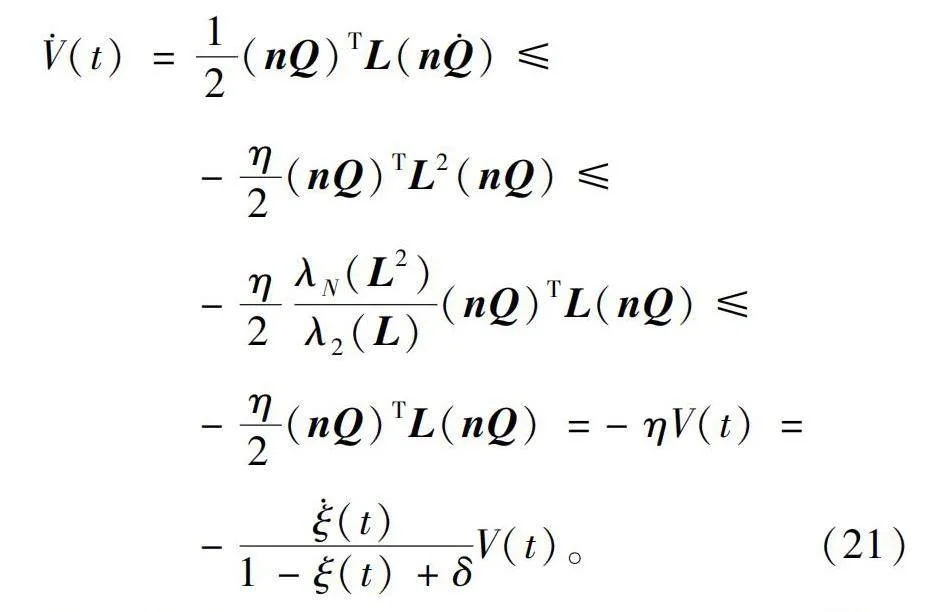
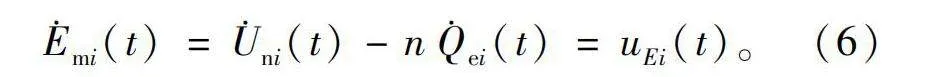
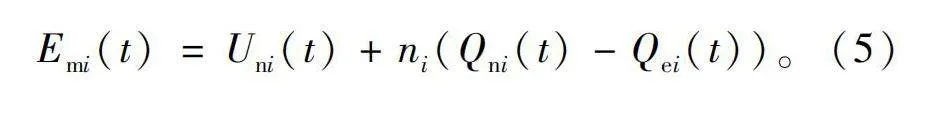
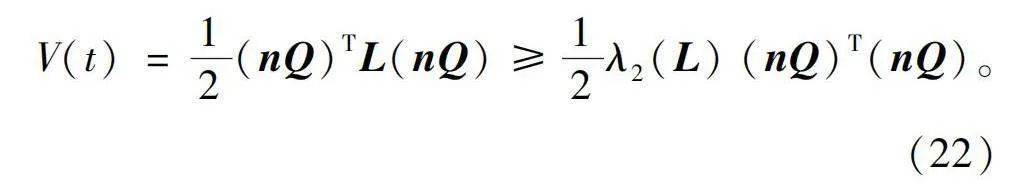
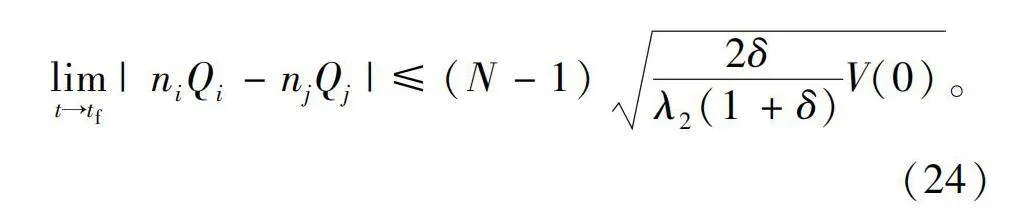
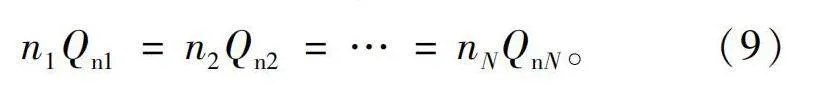
摘 要:针对孤岛微电网下虚拟同步发电机(VSG)一次控制存在的无功功率难以按照容量分配与电压偏差问题,提出一种基于预设时间一致性的分布式二次电压优化控制策略。该策略包含基于时基发生器的预设时间一致性算法以及与各分布式电源逆变器本体算法相结合的状态控制器,通过时基发生器将收敛时间提前确定,根据一致性算法对电压和功率输出偏差进行补偿,使逆变器仅依靠相邻单元之间的通讯即可实现无功功率分配与电压二次控制的目标。该策略无需考虑初始容量与协议参数的影响,保证了电压的定时快速恢复和无功功率的分配,同时收敛时间不受微电网容量扩展的影响,增加了微电网的灵活性和自由度。最后,通过仿真和实验验证了所提控制策略的可行性和有效性。
关键词:孤岛微电网;虚拟同步发电机;预设时间一致性;二次电压控制;电压定时快速恢复;时基发生器
DOI:10.15938/j.emc.2024.10.016
中图分类号:TM761
文献标志码:A
文章编号:1007-449X(2024)10-0166-11
收稿日期: 2023-02-02
基金项目:河南省科技攻关项目(232102240036);河南省自然科学基金(2122300410147);河南理工大学基础研究项目(NSFRF230616)
作者简介: 李 斌(1987—),男,博士,讲师,研究方向为新能源并网发电、微电网构架与控制;
龚祥祥(1997—),男,硕士研究生,研究方向为微电网分布式控制与稳定运行;
胡丹丹(1987—),女,本科,高级工程师,研究方向为电力系统及其自动化技术;
曾志辉(1978—),男,博士,副教授,研究方向为检测技术及信号处理;
王 浩(1988—),男,博士,讲师,研究方向为微电网稳定性分析。
通信作者:龚祥祥
Secondary voltage control of virtual synchronous generator based on preset time consistency
LI Bin1,2, GONG Xiangxiang1,2, HU Dandan3, ZENG Zhihui1, WANG Hao1,2
(1.School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454003, China;2.Henan International Joint Laboratory of Direct Drive and Control of Intelligent Equipment, Jiaozuo 454003, China;3.Jiaozuo Power Supply Company of State Grid Henan Electric Power Company, Jiaozuo 454003, China)
Abstract:Aiming at the problem of power distribution and voltage deviation in primary control of virtual synchronous generator (VSG) in isolated island microgrid, a distributed secondary voltage optimal control strategy based on preset time consistency was proposed. The strategy includes the preset time consistency algorithm based on the time base generator and the state controller combined with the algorithm of each distributed power inverter body, so that the inverter can realize the target of reactive power distribution and voltage secondary control only by relying on the communication of adjacent units. This strategy does not need to consider the impact of initial capacity and protocol parameters, which ensures the timing and rapid voltage recovery. Meanwhile, the convergence time is not affected by the capacity expansion of the microgrid, which increases the flexibility and freedom of the microgrid. Finally, feasibility and effectiveness of the proposed control strategy are verified by simulation and experiment.
Keywords:islanded microgrid;virtual synchronous generator;preset time consistency;secondary voltage control;voltage timing quick recovery;time base generator
0 引 言
微电网是一种小型的独立电力系统,它具有能够自我控制、保护和管理的特性。其中包含了分布式电源(distributed generator,DG)、储能模块(蓄电池、飞轮、超级电容器等)、变配电系统、负荷和控制系统。微电网既可以和大电网并网运行,也可以脱离大电网处在孤岛模式运行,处在孤岛模式时可以保障关键负荷的持续供电例如医院、军事基地和数据中心等[1]。目前应用的以电力电子变换器为接口的分布式电源,具有良好的灵活性和可控性,但是同时缺乏大电网所具有的惯性和阻尼,针对这一问题,有学者提出虚拟同步发电机(virtual synchronous generator,VSG)控制方法,该算法通过模拟同步发电机二阶模型,使分布式电源具有同步发电机的机电暂态特性和阻尼特性,提高了微电网对于DG的接纳能力,保障系统的稳定运行[1],自提出就受到了学者们的广泛关注。
然而,经典VSG控制方法只能实现一次控制[2],使微网系统具有一定的惯性和阻尼,并且可以根据容量进行功率的合理分配。在孤岛微电网中,此时没有大电网对于微电网进行支撑,因此抗扰动能力差,不够稳定,仅依靠VSG的一次有差控制,无法保证孤岛微电网的正常运行[3]。为了使控制可以无差,引入二次无差控制层来达到一次控制无法实现的控制目标。目前针对孤岛微电网的二次控制,可分为集中控制、分散控制和分布式控制三种类型[4]。集中控制(microgrid central controller,MGCC)主要通过中央控制器下达控制指令到微电网的各个单元进行控制,该控制系统对中央控制器的要求较高,依赖于复杂的通讯网络,通讯链路上的信息丢失都有可能造成相应单元故障,可靠性较低。分散式控制结构简单,可靠性高,但是却不涉及子系统之间的信息交互。分布式控制结合集中式控制以及分散式控制的优点,通过局部信息达到本地控制决策的全局优化[5]。对于孤岛模式运行的多机并联微电网系统,分布式的多智能体一致性控制可以仅通过与相邻智能体进行简单的状态信息交流,就可以使整个系统内的智能体都达到一致的稳定状态,由于其稳定、简单、高效的特点,如何将其应用在孤岛微网的电压频率无差控制中,已经是现阶段的研究重点。
在分布式一致性控制方案的各项性能指标中,收敛速度是其核心参数,决定着系统的运行性能和鲁棒性[6]。文献[7]提出一致性的收敛速度与第二小特征值的大小有关,可通过增大第二小特征值,达到优化的收敛效果。文献[8]将分布式的多智能体一致应用于孤岛微电网的二次控制当中,基于基本一致性原理提出一种分布式二次控制器,可以实现频率和电压恢复至额定值。在文献[8]的基础上,文献[9]通过引入分布式滑模控制器来提高控制器中比例和积分环节的收敛速度,该方案不仅可以提高系统收敛速度,系统的鲁棒性也由此提高,但是收敛时间仍然处于无穷远处。文献[10-13]引入基本时间一致性方案,可以使系统在一定时间内完成收敛,但是由于基本一致性的收敛时间的确定依赖于微电网的初始状态,因此具体的收敛时间依然难以确定,其中,文献[11]还列举了6个分布式电源的不同结构,验证收敛时间受网络通讯结构的影响,提出优化网络通讯结构可以提高收敛速度,但是未考虑DG数量的增多对收敛速度的影响。文献[14-17]提出一种引入固定时间一致性算法的控制方案,相比于有限时间一致性,该方案的收敛时间与系统的初始状态无关,可以使二次控制过程更快速,确保了电压和频率的更快恢复,但是协议参数会对初始状态的差值进行放大,对微电网的结构产生不利影响,其中,文献[17]分析了7个DG同时进行控制时的快速恢复性能,通过与文献[16]中3个DG的性能对比可知,DG数量的增多同样存在收敛时间变长,与估计收敛时间差值过大的影响。
上述研究对一致性在微电网的应用进行初步分析。然而对于现阶段的一致性二次控制仍然存在诸如初始状态、协议参数和DG数量变化的限制条件,难以确保微电网电压与频率的快速恢复,因此针对以上问题,将基于时基发生器(time base generator,TBG)的预设时间一致性控制策略引入到状态控制器,通过进一步对状态控制器中平均电压观测器与无功功率控制器的改进设计,达到VSG电压定时恢复的二次控制目的。该控制器仅需相邻DG之间的少量通讯便可在预设时刻解决一次控制存在的偏差问题,相比于传统的引入多智能体一致性算法的二次控制,引入可以由用户自定义收敛时间的时基发生器,解决目前结合一致性的二次控制电压受到初始条件和系统容量等参数的限制问题。在保证系统能够在设定时间内达到收敛的同时,还能够对于系统的灵活性和可靠性有一定程度的提升。最后,通过合理的仿真以及实验设计对于提出的控制算法进行验证。
1 VSG的一次控制
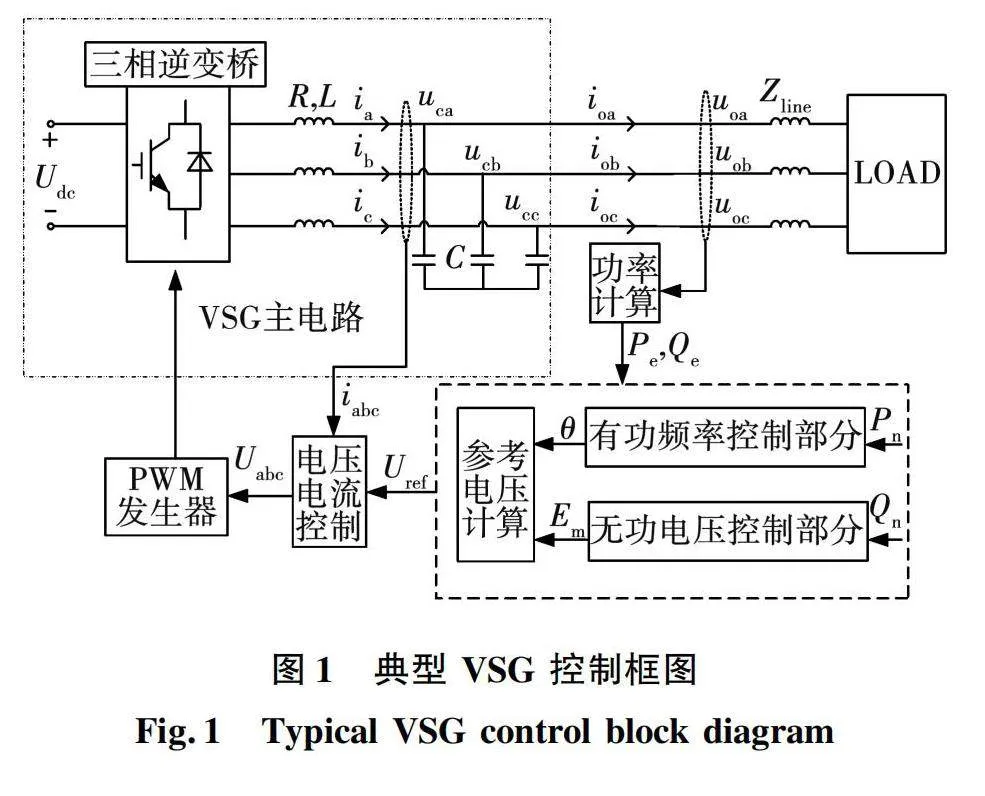
典型的VSG控制方式主要通过在主电路计算得来的有功无功,分别经过有功频率控制部分以及无功电压控制部分生成电压幅值和相位,通过幅值和相位计算出参考电压,参考电压经由电压电流双闭环控制输出,再由PWM发生器产生逆变器的工作信号。VSG控制框图如图1所示,主要包含VSG主电路以及控制电路部分。直流侧应用含有储能元件的分布式电源,在这里使用直流电源Udc代替。主电路由逆变器、滤波元件、线路等效而成的阻抗Zline、等效负荷部分和对于线路上必要参数进行测量的元件组成。ia、ib、ic分别为逆变器输出电流,uc为逆变器交流侧电压。
VSG控制策略主要通过模拟同步发电机的机械特性和电磁特性来解决系统频率突变的问题,并且具有抑制功率震荡的能力。在有功环路的控制方面,通过改善参数以及增加二次调频的方案达到稳定有功频率的目的;可以改进VSG的控制结构,添加二次调频控制策略使其适用于孤岛模式的微电网[18];可以设计自适应虚拟阻抗来稳定频率[19]。对于二次调频方案很多学者提出改进,有功环的二次调频在文中不做重点介绍。
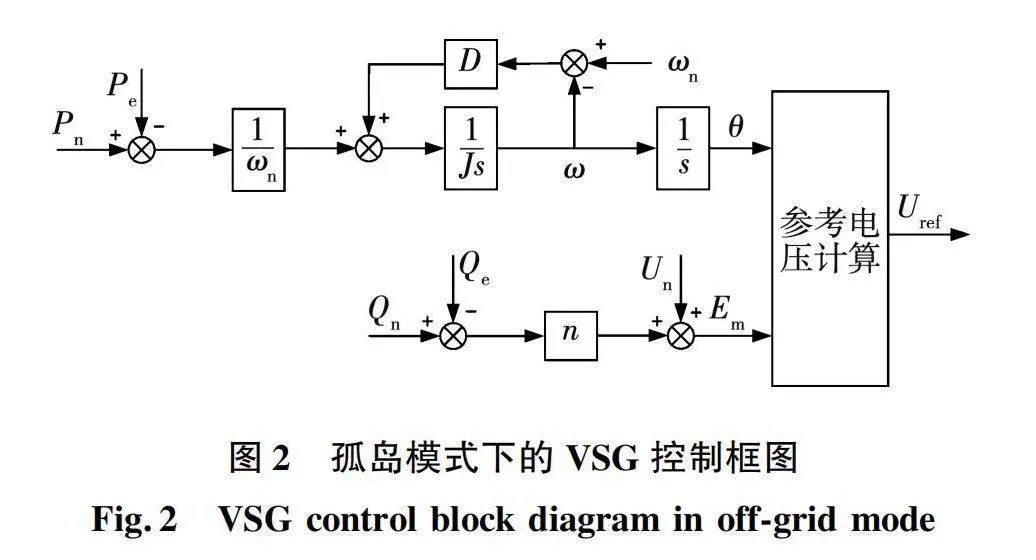
在孤岛模式下的虚拟同步发电机输出的无功功率主要由负载决定,VSG会为负载提供所要求的电压幅值。图2为孤岛模式下的VSG功率控制环路,其中:Pe,Qe分别为输出的有功功率和无功功率;Pn,Qn分别为额定的有功和无功功率;J为VSG模拟的转动惯量;D为VSG模拟的阻尼系数;ωn为根据大电网设置的额定角速度;ω为VSG电气角速度;θ为角度;n为下垂系数;Un为额定电压;Em为电压幅值。
基础VSG算法所具有的电压和无功一次控制本质上还是下垂控制,依然是有差控制,微电网内的负荷或者线路波动依然会导致电压与额定值有偏差,所以为保证微电网电压稳定在额定值需要引入二次控制,鉴于多智能体一致性算法的优越性,本次研究将其引入到VSG无功控制环路来实现二次控制。
2 VSG的二次控制
2.1 图论
存在V={1,2,…,N}表示通讯节点个数集合,若有N个多智能体组成的连通图,则称有向图G=(V,E,A)为连通图,E∈V*V是无向图的边集,A=[aij]为邻接矩阵用来表示节点间的通信关系,如果代理j代理点i传递状态信息,则aij=1,不然aij=0。当节点与节点之间只能进行单向传输通讯时,传输特性称之为有向图,有向图为aij=aji的双向通讯时,也称之为无向图。如果从任意节点出发能够经过所有节点,则称图G有生成树或连通图,有生成树是实现控制算法的必要条件。Ni={j∈V|(j,i)∈E}表示节点i的邻居节点集合。
微网系统的通信系统采用无向图进行设计,无向图的入度矩阵与出度矩阵相同,后续统称为度矩阵D。与交互信息相关的拉普拉斯矩阵L=D-A,在整个多智能体系统中占据着举足轻重的地位。
2.2 基于TBG的预设时间一致性
在现阶段微电网的二次控制中多采用固定时间一致性控制[21],在平均一致性的基础上进行改进,通过确定收敛时间进而提高收敛速度,同时收敛时间不会受到初始状态的影响,固定时间一致性的典型结构在文献[22]中进行详细介绍,具体表达式为
ui=α(∑j∈Niaij(xj(t)-xi(t)))pq+β(∑j∈Niaij(xj(t)-xi(t)))uv。(1)
式中:pgt;qgt;0,vgt;ugt;0,αgt;0,βgt;0均为常数,表示需要根据情况进行设计的算法参数。该算法可以通过下式估算收敛时间的上限,即
T0≤Tmax=1λ2(L)Np-q2qαqp-q+1βvv-u。(2)
式中λ2(L)是L阵第二小特征值。多智能体固定时间一致性算法虽然存在可以估算收敛时间的算式,但是所计算的结果过于保守,难以准确反映实际运行的收敛时间,且在微电网DG数量增多时实际收敛速度会下降。
为了解决现阶段固定时间一致性存在的收敛问题,基于TBG的预设时间一致性在文献[23]中被提出,具体结构为
ui(t)=-ξ·(t)2λ2(L)(1-ξ(t)+δ)+1×(∑j∈Niaij(xi(t)-xj(t)))。(3)
式中:0lt;δ1;ξ(t)为TBG,是研究中可预设时间的核心,可能会发生以下故障:
1)ξ(t)=0,TBG发生不可用故障导致二次控制失去定时作用,无法按照设定时间恢复电压;
2)ξ(t)突变为任意值,TBG将发生对二次控制的加速不可控,预设时间无法确定,失去预设作用;
3)ξ·(0)≠0,TBG无法消除多DG之间的状态偏差,导致电压恢复时间受初始状态的影响。
为避免发生上述故障,ξ(t)需要满足以下几点要求:
1)ξ(t)在(0~∞)保持大于0。
2)ξ(t)在时间初值(0~tf)单调递增,并且ξ(0)=0,ξ(tf)=1以及保证tf∈(0~∞)。
3)ξ·(0)=ξ·(tf)=0。
4)在预设时间域外,即(tf~∞)时刻,ξ(t)=1,ξ·(t)=0。
通过满足以上要求,设计ξ(t)如下:
ξ(t)=10t6ft6-24t5ft5+15t4ft4,0≤t≤tf;1,tgt;tf。(4)
式中tf是收敛时间,用户可以根据需要自行设计,不会被参数与初始值限制。此外,由于ξ·(t)的存在,当初始值相差过大时也不会影响收敛性能。
2.3 VSG二次电压控制策略设计
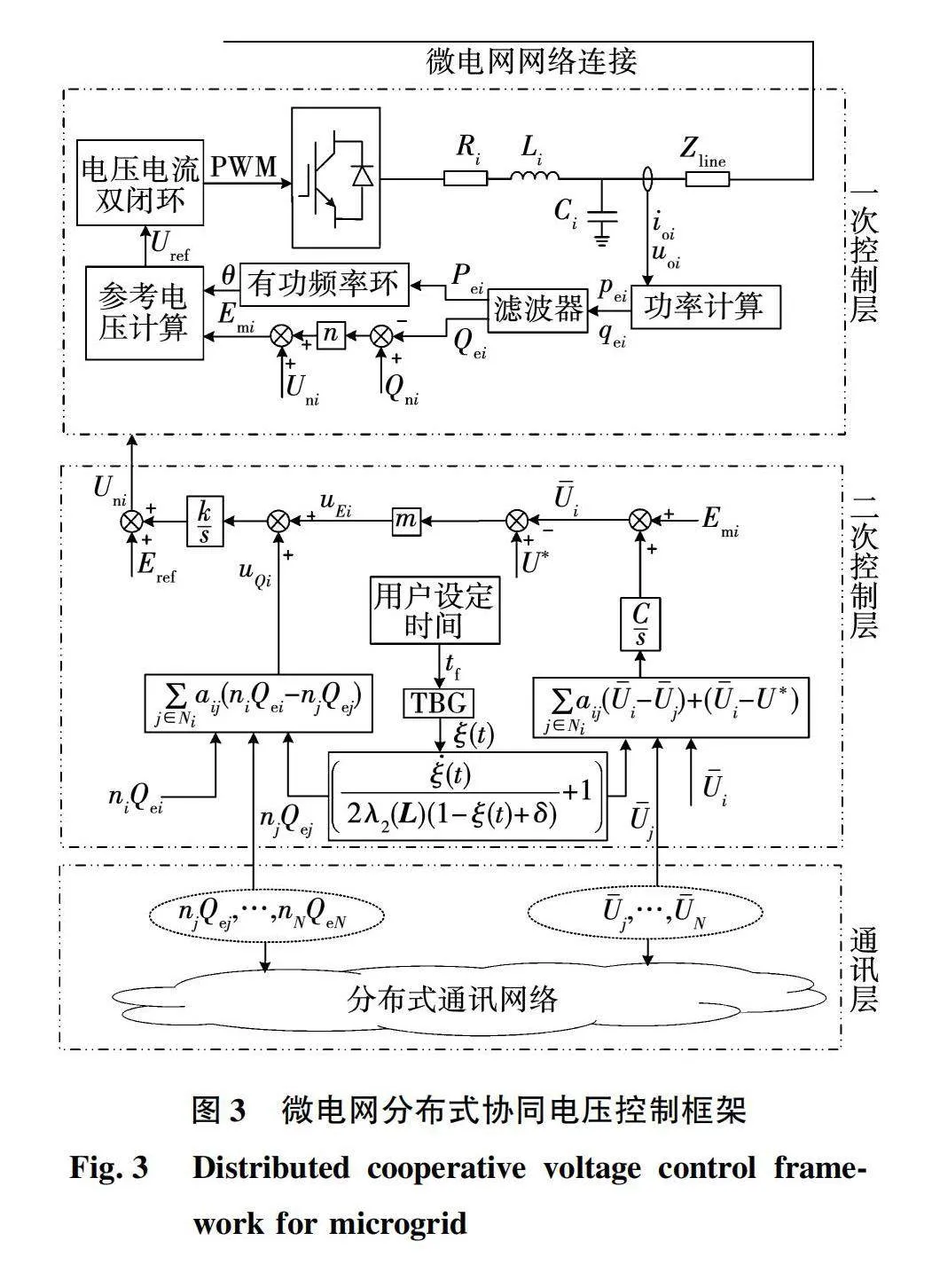
由于VSG一次控制难以保证分布式电源输出电压的稳定以及无功分配的精确均分,本次研究提出的基于预设时间一致性的二次控制策略能够解决一次控制带来的偏差问题,同时保证了电压的快速定时恢复,主要是对无功功率偏差与平均电压偏差控制模块进行改进达到微电网输出电压稳定在额定值的目的,单个DG的拟定分布式电压控制框图如图3所示。
对VSG的二次控制应用分布式协同一致性构建动态模型。为保持电压稳定,构建第i台DG的无功电压方程为
Emi(t)=Uni(t)+ni(Qni(t)-Qei(t))。(5)
其中:Emi(t)定义为第i台DG的输出电压参考信号;Uni(t)、Qni(t)分别为额定电压和额定无功;Qei(t)为输出无功功率;ni表示无功电压方程的下垂系数;对式(5)求导得
E·mi(t)=U·ni(t)-nQ·ei(t)=uEi(t)。(6)
式中uEi(t)为需要设计的平均电压偏差控制器。
另外有
nQ·ei(t)=uQi(t)。(7)
其中uQi(t)为无功功率偏差控制器。根据式(6)和式(7)得出分布式协调一致性调节后的额定电压为
Uni(t)=k∫[uQi(t)+uEi(t)]dt+Eref。(8)
式中:Eref为系统额定电压参考值,在t=0时,Eref=Uni(0)=311 V;等式右侧第一项表示基于预设时间一致性的改进状态控制器;k表示状态控制器的积分项系数。
下面具体设计控制器各项,根据式(5)所示的无功电压方程可以得出电压偏差与功率偏差成比例关系,选取逆变器电压的下垂系数与分布式电源的无功功率容量成反比的条件,即
n1Qn1=n2Qn2=…=nNQnN。(9)
式中Qni表示分布式电源的无功功率容量,如按照容量进行分配,需要满足:
Qe1Qn1=Qe2Qn2=…=QeNQnN。(10)
因此,输出无功功率与下垂系数也同样满足:
n1Qe1=n2Qe2=…=nNQeN。(11)
通过分布式协同预设时间一致性算法实现无功按照容量分配的目的,无功功率的偏差为
uQi=niQ·ei=-ξ·(t)2λ2(L)(1-ξ(t)+δ)+1×
(∑j∈Niaij(niQei-njQej))。(12)
式中:uQi表示第i个分布式电源的无功功率偏差;δ为自定义常数项,一般有0lt;δ1;ξ(t)为TBG;λ2(L)为拉普拉斯矩阵的第二小特征值;aij为无功功率通讯关系;Qei(t)为输出无功功率;ni表示无功电压方程的下垂系数。
VSG一次控制引起的电压偏差问题需要二次控制进行调节,但是由于线路阻抗的不同,输出电压难以保持一致,因此微电网中各DG的输出电压应调节在额定电压的可接受范围之内。二次电压控制将系统的平均电压恢复至额定值U*,使得各分布式电源的输出端电压幅值能够稳定在额定值附近,通过预设时间一致性设计的分布式协同平均电压观测器,以此获得微电网的平均电压为
U-i=Emi+C∫[-(ξ·(t)2λ2(L)(1-ξ(t)+δ)+1)×
(∑j∈Niaij(U-i-U-j)+(U-i-U*))]dt。(13)
式中:Ui,Uj为第i个和第j个分布式电源的平均电压观测值;Emi(t)为第i台DG的输出电压参考信号;U*为微电网的参考电压;C为电压耦合系数。将平均电压Ui和微电网的参考电压U*进行比较,产生电压差值,设计平均电压偏差控制器为
uEi(t)=m(U*-U-i)。(14)
式中m表示无功均分与电压恢复的权重系数。
因此根据式(5)~式(14)对改进状态控制器的设计,得出基于预设时间一致性的VSG二次电压控制策略表示为:
Emi(t)=Uni(t)+n(Qni(t)-Qei(t));
Uni(t)=k∫[uQi(t)+uEi(t)]dt+Eref。(15)
当微电网达到稳定状态时,有uQi=0,此时满足式(10),无功功率实现按容量进行分配,同样地,在稳定状态下Ui=Uref实现平均电压恢复至额定值的控制目标,完成状态控制器的二次控制任务。
2.4 控制策略的收敛稳定性证明
为了保证式(15)所提二次电压控制器设计的稳定性,对其进行推理证明。首先,根据图论部分知识,引用相关专业的部分定义和引理。
定义1:对于初始条件xi(0),最终如果需要保持一致性收敛,则需要满足:
式中:C为极小的常数,表示收敛效果,相邻单元与本地单元的差值足够小,则称之为收敛完成;tf表示所要设定的收敛时刻,超出设定时刻需要保证收敛完成,与初始条件无关。
引理1:对无向连通图需要满足:
xTLx≥λ2(L)xTx;
xT(L2)x≤λN(L2)xTx。(17)
式中λ2(L)和λN(L2)分别为第二小特征值和最大特征值。式(17)说明了系统拓扑结构的拉普拉斯矩阵和拉普拉斯矩阵的平方与对应特征值的关系需要满足上述条件。
引理2:对于一阶线性系统,令式(3)中的ξ·(t)/[2λ2(L)(1-ξ(t)+δ)]=η,对应矩阵形式表示为
x·i(t)=-(η+1)LX。(18)
对式(18)两边同时积分可以得到
x(t)=x0(1-ξ(t)1+δ)。(19)
此时,0lt;δ1,ξ(tf)=1,因此在tf处x(t)的收敛效果接近于极小值[δ/(1+δ)]x0。
定理1:根据定义与引理1、2,所设计的无功功率偏差控制器式(12)具有如下收敛条件:
当无功偏差控制器遵循定理1时,完成功率调节。现对定理1给予证明,为简化计算需要构建V(t)=[(nQ)TL(nQ)]/2李雅普诺夫方程,L表示半正定矩阵,对两边同时微分并结合引理1有
V·(t)=12(nQ)TL(nQ·)≤
-η2(nQ)TL2(nQ)≤
-η2λN(L2)λ2(L)(nQ)TL(nQ)≤
-η2(nQ)TL(nQ)=-ηV(t)=
-ξ·(t)1-ξ(t)+δV(t)。(21)
结合引理2有V(t)≤[δ/(1+δ)]V(0)。将引理1状态变量x(t)替代为所提二次控制的状态变量可以推导
V(t)=12(nQ)TL(nQ)≥12λ2(L)(nQ)T(nQ)。(22)
移项计算有
limt→tf|nQ|≤2λ2V(t)≤2λ2δ1+δV(0)。(23)
得到预设时间tf处的收敛值为
limt→tf|niQi-njQj|≤(N-1)2δλ2(1+δ)V(0)。(24)
式(24)不等式右边部分由于δ取值极小,因此约等于0,此时收敛效果得到保证。
为保证基于TBG的预设时间一致性能够在tgt;tf时,仍能够维持稳定收敛状态,对式(22)微分有
V·(t)=-η+12(nQ)TL2(nQ)=
-12(nQ)TL2(nQ)≤0。(25)
通过数学知识可知V(t)是一个单调不增函数,在tgt;tf时存在
|niQi-njQj|≤(N-1)2δλ2(1+δ)V(0),tgt;tf。(26)
式(26)的右半部分是个极小值,因此在超出设定时刻以外的时间仍然可以保证收敛效果,即
limt→∞|niQi-njQj|=0。(27)
式(13)所示的电压观测器是由牵制一致性改进而来,证明需要构建李雅普诺夫函数V(t)=(xTPx)/2,其中:P为正定实对称矩阵;x表示状态矩阵集合,这里指平均电压。左右两边求导可得
V·(t)=12xTPx·=-(η+1)2xTP(L+E)x。(28)
式中:E为单位矩阵;L为半正定矩阵;P(L+E)gt;0;根据李雅普诺夫稳定性第二判据V(t)gt;0;V·(t)lt;0,系统式(13)渐近稳定。
根据以上证明得出无功功率偏差控制器在时间全域的收敛稳定性,状态控制器在无功功率精确分配时会遵循定理1,且在预设时刻δ取值很小时,初始状态对收敛值的影响会变得微乎其微,进而无功功率之间的差值会保持在稳定范围以内,并且参数与初始状态不会对收敛时间产生影响。
3 仿真和实验
3.1 仿真验证
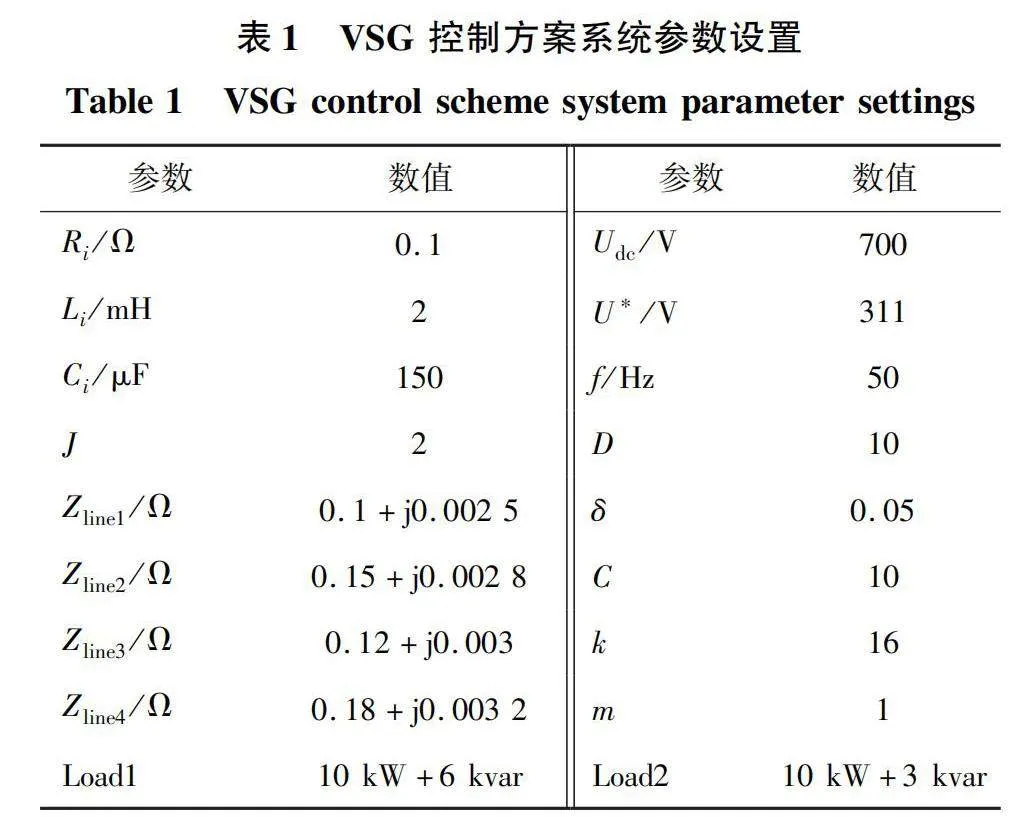
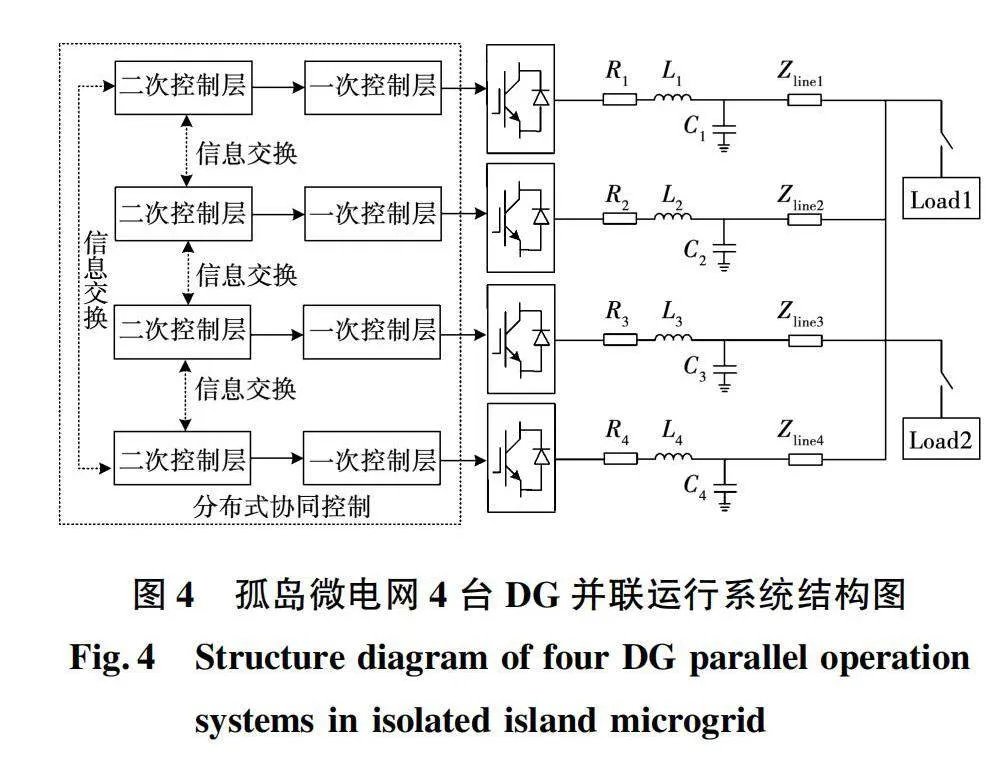
对于提出的预设时间一致性的二次电压控制方法,仿真部分使用仿真平台搭建了如图4所示模型,对于4台DG的输出电压和无功功率进行仿真,将4个DG的通讯拓扑优化,并对结果进行分析。相关参数如表1所示。
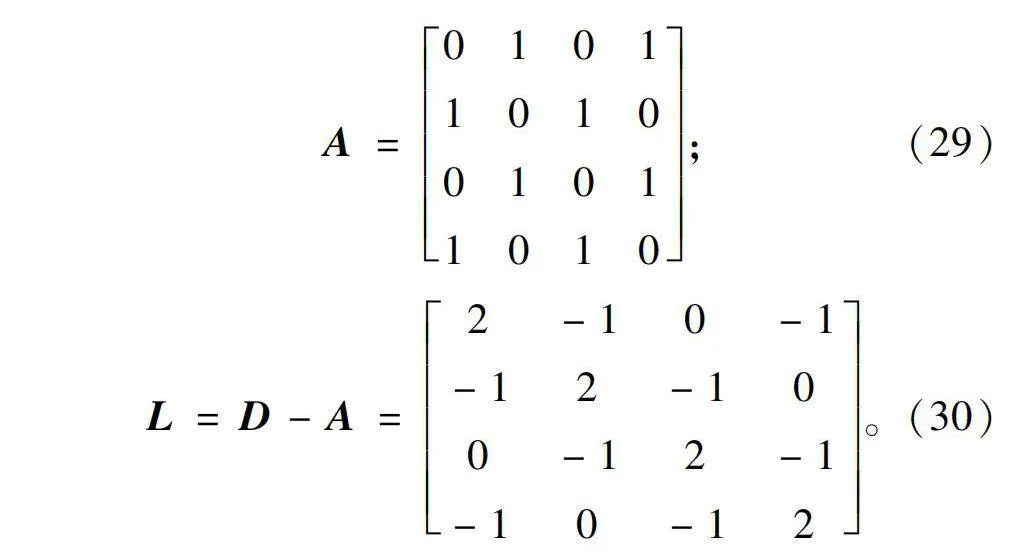
根据图4所示的4台DG并联运行系统结构图,并根据图论部分知识可以计算出邻接矩阵和拉普拉斯矩阵为:
A=0101101001011010;(29)
L=D-A=2-10-1-12-100-12-1-10-12。(30)
式中A阵中aij=1表示相对应分布式电源之间有通讯关系。
根据前文给出的L阵得出L阵第二小的特征值为λ2(L)=2,代入预设时间一致性中可以得到预设时间的关键项,且不含其余未知系统参数。
1)算例1:验证所提二次电压控制策略的二次恢复性能。构建4台容量相同的DG,下垂系数n统一为5×10-4,运行在并联孤岛模式下,初始时刻仅通过虚拟同步发电机控制,在时间3 s时刻引入基于预设时间一致性的二次电压控制策略,预设时间设定为加入后的1 s。
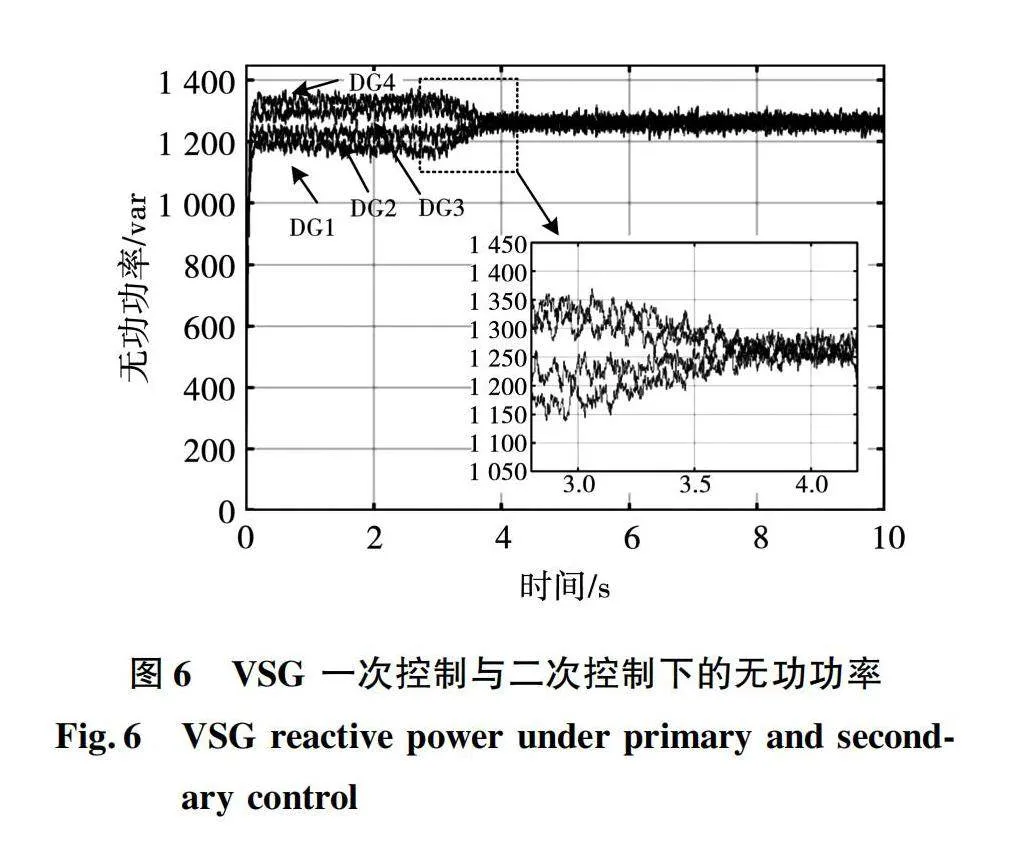
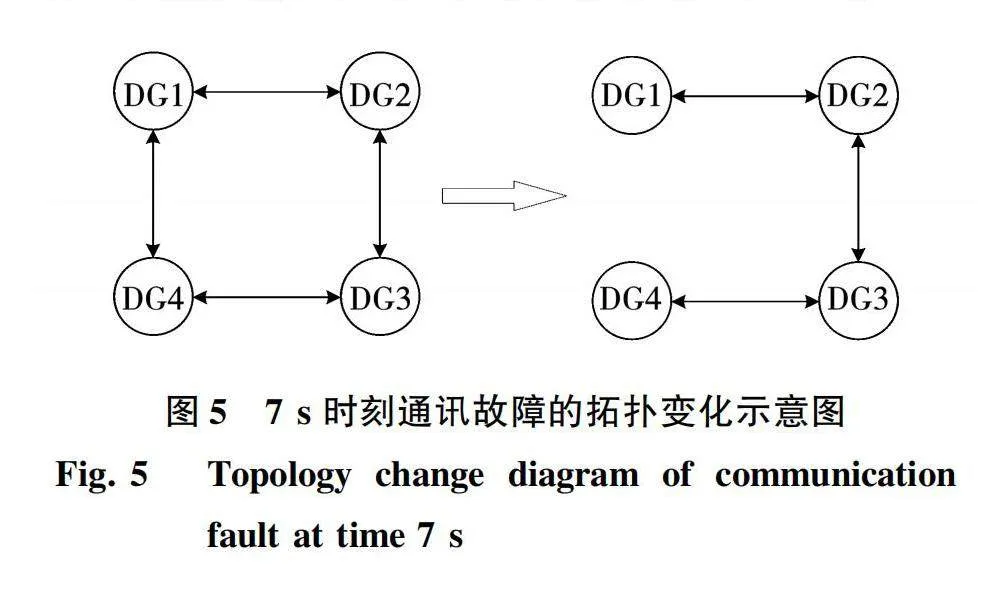
在7 s时刻模拟通讯失效的故障运行,DG1和DG4之间的连接线断开如图5所示,仿真波形如图6所示,在保证拓扑含有生成树的前提下,通讯失效对系统控制性能几乎没有影响。从图6可知,一次控制下功率由于线路阻抗、发电特性等原因导致功率偏离额定值,3 s加入预设时间一致性后,功率经过小幅振荡在预先设定的时间趋近于一致。
从以上描述的结果可以得出,基于预设时间一致性设计的二次电压控制策略可以有效地改善一次控制存在的偏差问题,另外即使存在通讯失效的问题,但只要存在生成树就不会对原有结果产生大的影响。这一仿真结果证明了通过分布式协同一致性设计的二次控制策略具备稳定收敛效果。
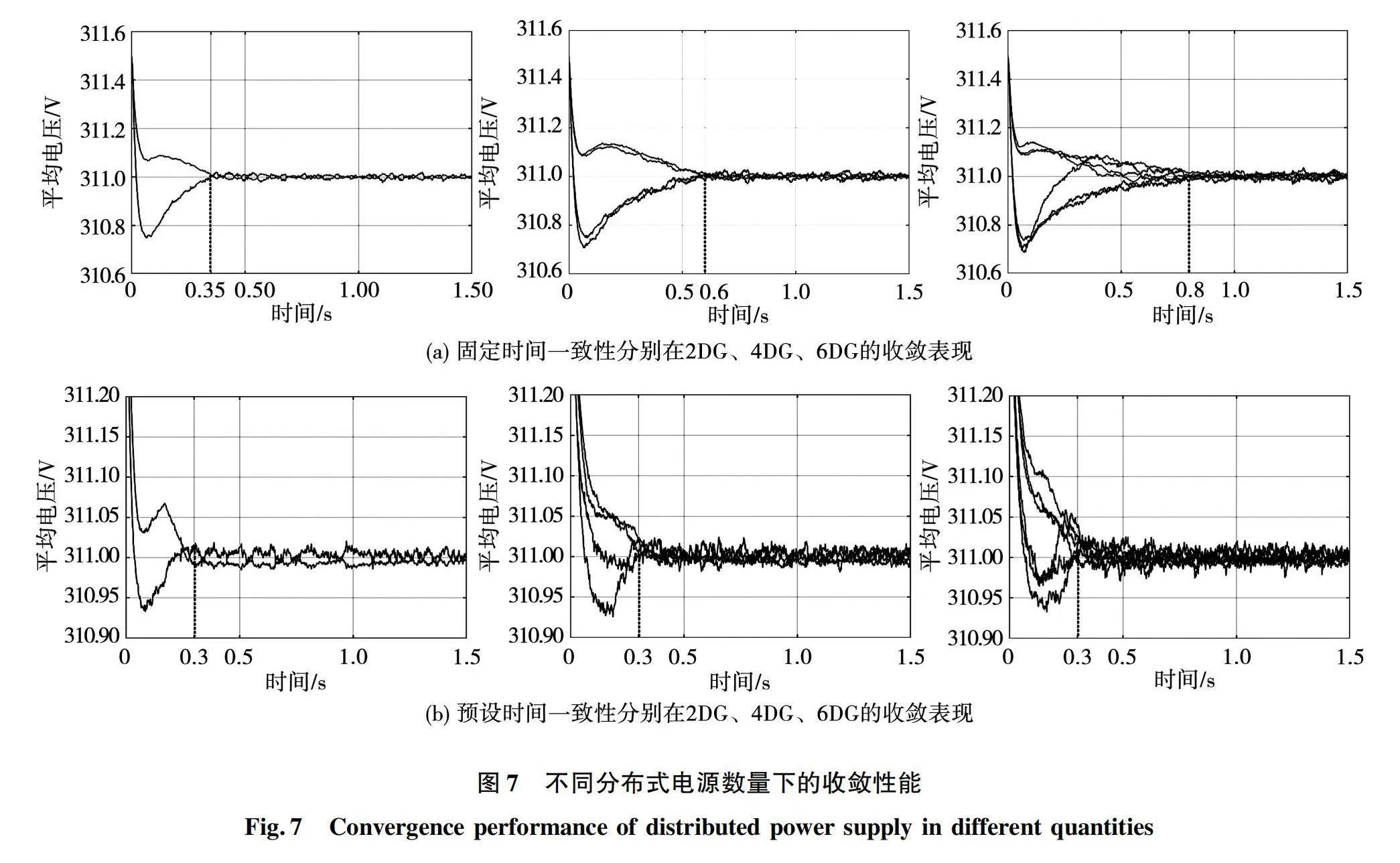
2)算例2:验证预设时间对比现阶段固定时间一致性运用在不同数量DG下的收敛速度优势。分别构建2台DG、4台DG以及6台DG,其中1 000、2 000 W容量均匀分布。图7的仿真结果表示对固定时间一致性与预设时间一致性在不同数量DG结构下的收敛性能进行对比,本次分布式一致性皆采用经典策略,未对一致性进行收敛加速的改进。
如图7所示,固定时间一致性在2台DG、4台DG以及6台DG的收敛时间分别为0.35、0.6、0.8 s。固定时间一致性的收敛效果会受到DG数量的影响,而相对于本次研究所使用的预设时间一致性对于不同数量的DG均可保证在0.3 s收敛。
由此可见,预设时间一致性在DG数量增多的情况下仍然可以保证快速收敛,而对于固定时间一致性在不同数量的DG下,功率的恢复速度受到不同程度的影响。随着新能源的不断发展,分布式电源的数量也在逐渐增多,本次研究设计的二次电压控制策略保证了多DG下的稳定恢复速度,验证了所提控制策略的优势所在。
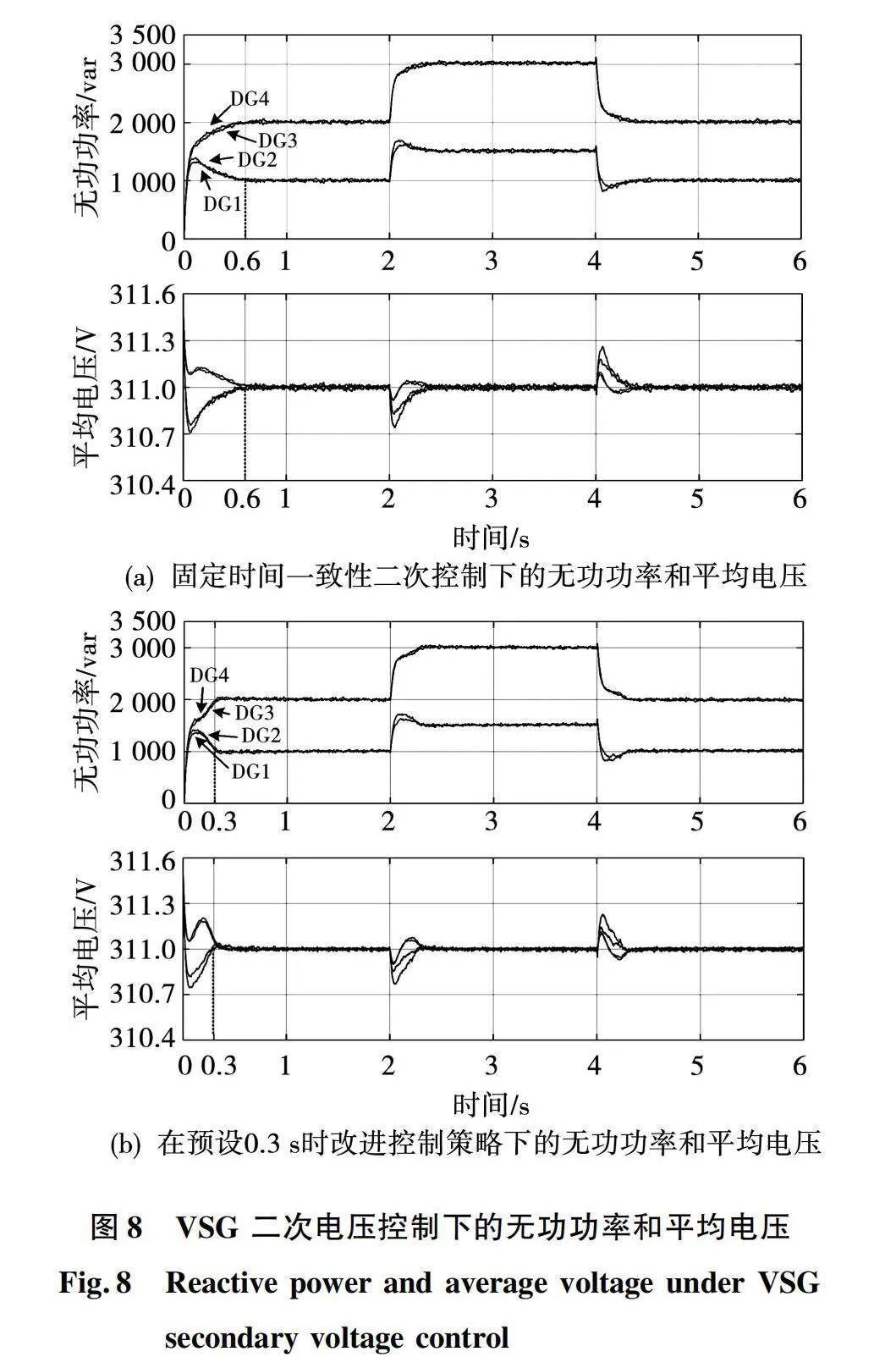
3)算例3:验证所提改进二次控制策略对比现阶段固定时间一致性下的二次控制对平均电压以及无功功率的收敛变化状态。对预设时间一致性的收敛优势进行验证,将4台DG的额定容量之比调为1∶1∶2∶2,分别为无功下垂系数n的取值与额定容量成反比设计下垂系数,有DG1和DG2的下垂系数为5×10-4,DG3和DG4的下垂系数为2.5×10-4。初始时刻仅有无功功率为6 kvar的Load1工作,在2 s时增加无功功率为3 kvar的Load2,通过对比分析所提预设时间在微电网应用中的优势。
如图8(a)所示,由于分布式协同一致性的控制无功功率与平均电压均能恢复到稳定状态,但是传统策略下恢复稳定时间为0.6 s,相比于图8(b)所示的基于预设时间一致性的二次控制策略,同样是达到稳定状态,但是恢复时间可以稳定在0.3 s内。
从结果显示,基于预设时间一致性设计的二次控制可以在预设时间内使电压恢复到额定值,相比于固定时间一致性方法设计的二次控制的恢复速度更快,也更准确,并且与现有的研究相比收敛时间可以自定义,可以使微电网更加灵活和高效。
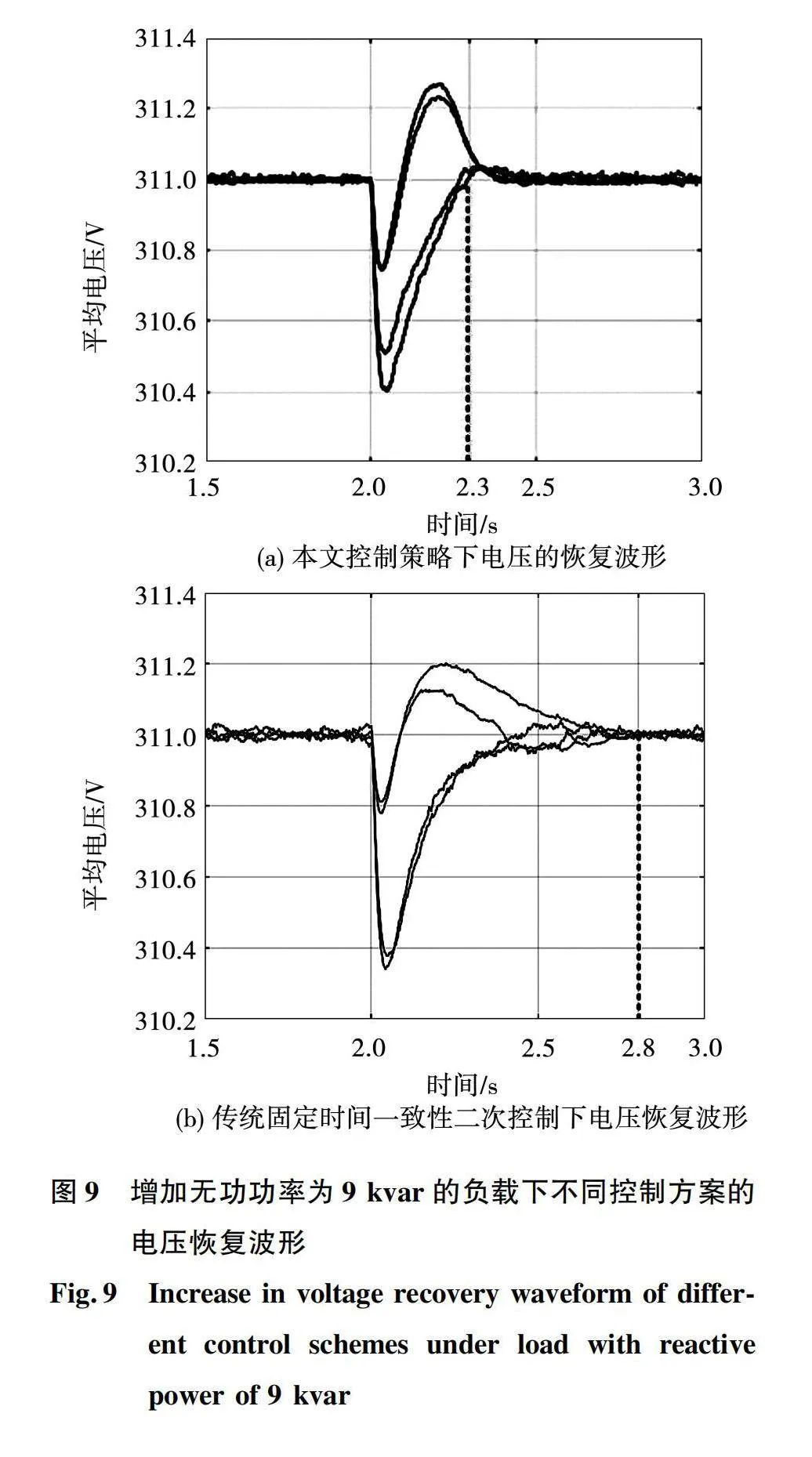
另外需要说明的是,考虑到过大的负载难以在极短的时间内达到所需要恢复的额定值,为保证良好的恢复效果,预设时间需要根据实际负载进行设计。如果已经将预设时间固定,负载的增加范围较大时会适当延长预设的收敛时间,以提高其适用性。如图8(b)所示,在2.3 s时无功功率为3 kvar的负载电压能够很好地恢复,将负载换为无功功率为9 kvar时恢复效果有一定偏差,如图9(a)所示。但是相对于传统固定时间一致性二次控制方案,如图9(b)所示,预设时间一致性仍然可以保证快速恢复的优势。
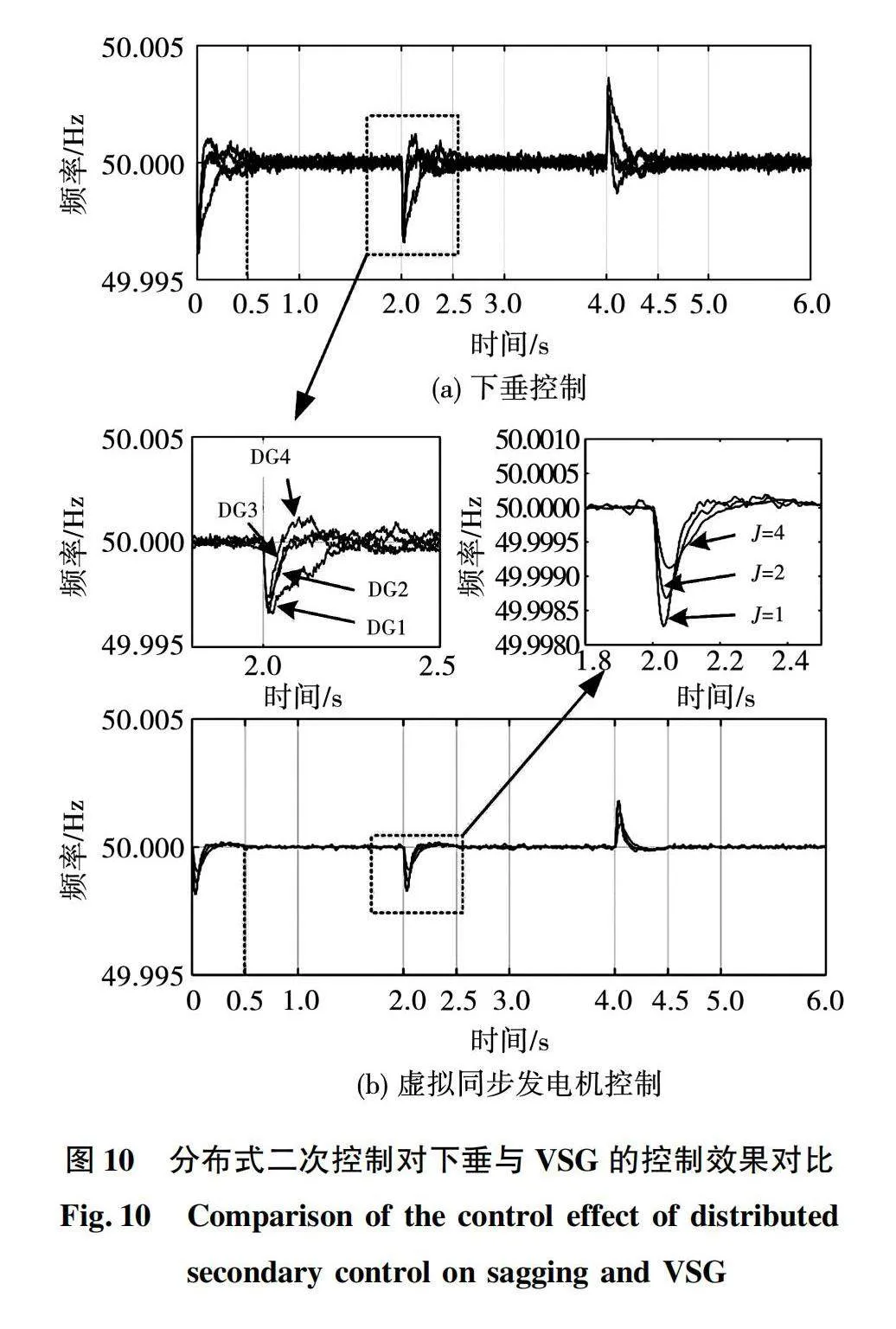
4)算例4:下垂控制与所提出控制方法的控制效果对比。运行工况为初始时刻Load1工作,2 s时增加Load2,4 s时刻卸除负载Load2。仿真结果如图10所示,图10(a)下垂控制分别为4台DG在预设0.5 s时刻收敛的频率波形,图10(b)为转动惯量参数分别为1、2、4时DG1的频率运行波形。从仿真结果可知,随着转动惯量的增大,曲线向后移动,达到峰值的时间增加。因此,基于虚拟同步发电机设计的二次控制可以通过增大转动惯量,进而增大微电网的惯量。而常规的下垂控制,虽然在预设时间一致性的作用下满足频率的快速恢复,但是DG的频率很快达到峰值,并且系统惯量很小。因此,基于虚拟同步发电机的二次电压控制相比较于下垂控制,能够为系统提供一定的虚拟惯量。
3.2 实验验证
在软件仿真当中已经验证了本研究设计的控制策略的有效性,接下来将使用TMS320F28335控制器进行实验验证部分,实验主要由控制器对仿真机内的主电路进行控制,并通过示波器观察控制结果,最终的结论能够进一步验证控制策略和仿真实验的正确性。但是由于实验条件的限制,本次实验仅采用3台DG,并给予两两通讯的条件,实验参数如表1所示。
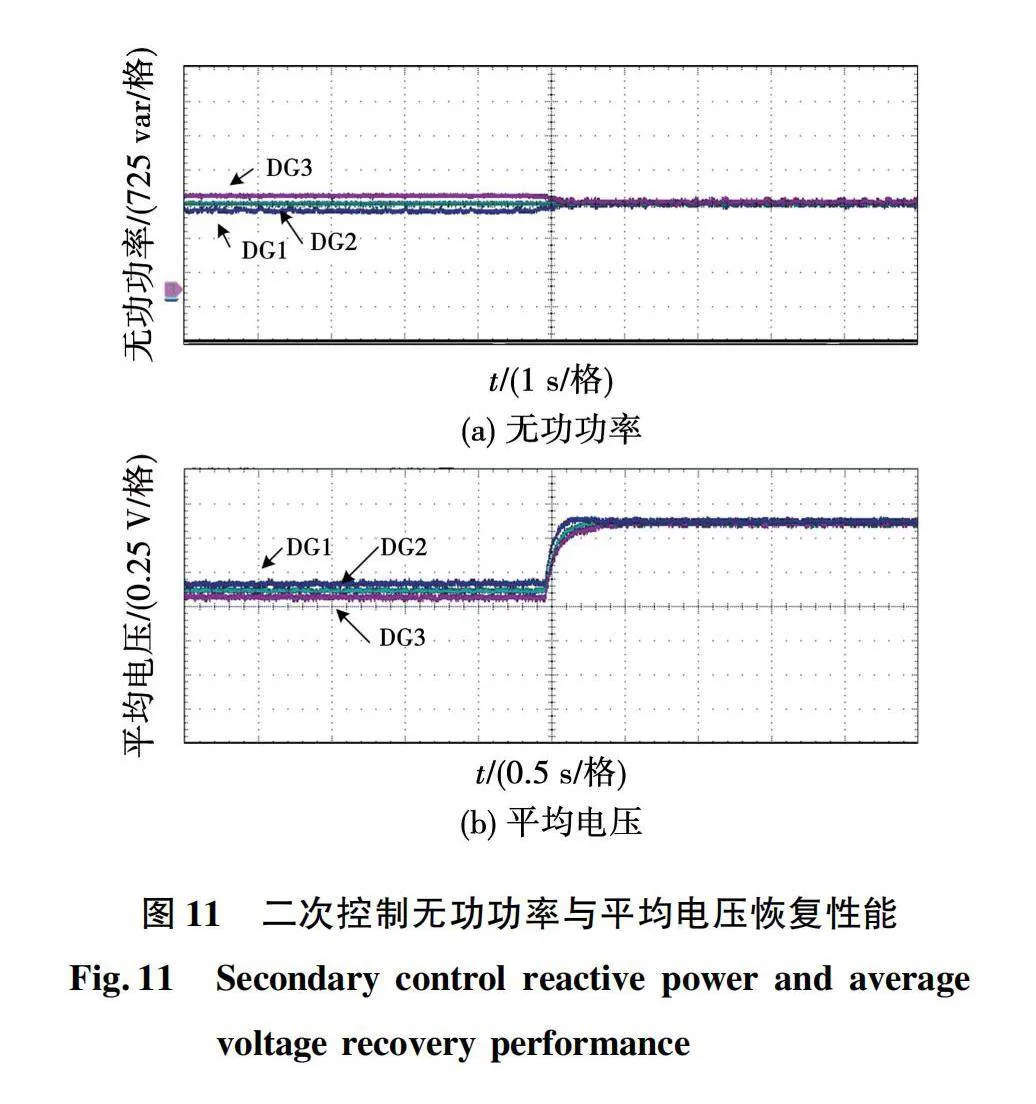
1)工况1:验证二次控制效果。设3台DG的容量相同,初始时刻为VSG一次控制,一定时间之后开始引入所提二次控制策略,实验全程只接入Load1。如图11所示,在一次控制下电压和功率存在偏差,引入二次控制之后,将收敛时间设定为引入后的0.5 s,3台DG因为容量一致,无功功率均稳定到2 000 var;平均电压也从310.5 V左右恢复到额定值311 V,由于电压恢复偏差只有0.5 V左右,为了更好地观察二次电压恢复过程取局部放大图。从显示的结果可以看出,此次研究设计二次控制策略的无差控制特性。
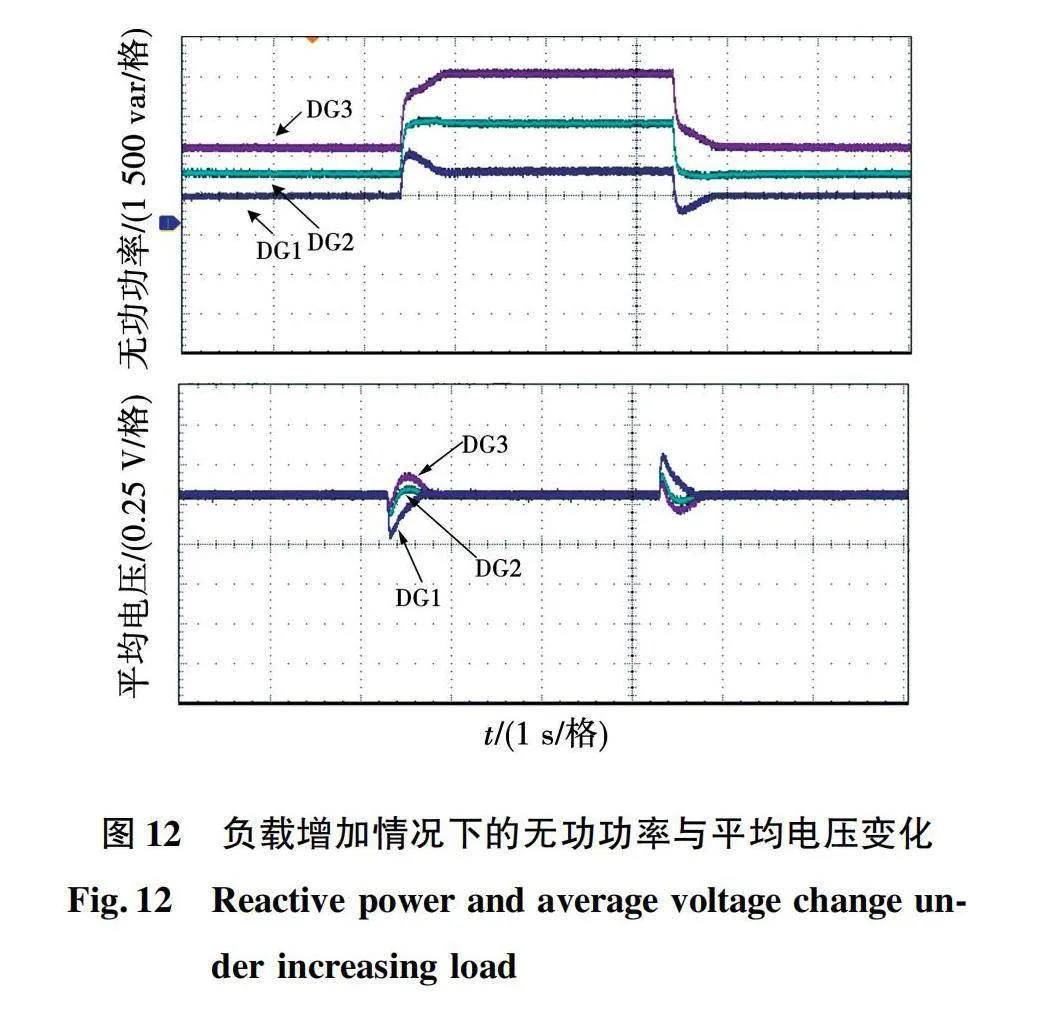
2)工况2:验证微电网孤岛模式VSG控制下负载增加时无功功率分配以及平均电压恢复的性能。3台DG的容量比为1∶2∶3,在基于预设时间一致性的VSG二次电压控制下,实验设定为初始时刻时负载无功为6 kvar,在一段时间后负荷突变为9 kvar,恢复时间设定为负载突变后的0.5 s。
本次实验结果如图12所示,初始时刻时无功按照各DG 1∶2∶3的容量进行分配,负载突变后3台DG的无功功率分别又增加1 000、2 000、3 000 var,在到达提前预设的恢复时间0.5 s后系统稳定,此时无功再次按照容量分配,电压此时经过0.5 s也稳定在额定值。
根据实验结果分析可得,本文所设计的二次控制算法电压恢复和无功分配方面均有良好的性能,不仅能保证实际收敛时间与预设时间一致,还能保证无功按容量分配和电压稳定在额定值。二次控制快速稳定性能验证了预设时间一致性二次控制策略设计的初衷。
4 结 论
本文所设计的控制策略将多智能体一致性算法应用到虚拟同步发电机当中,设计了一种可预设时间的分布式二次电压控制。通过仿真和实验结果进一步验证所提控制策略的可行性和准确性,同时通过调节负荷的大小、模拟通讯失效、调整分布式电源数量规模等条件进一步说明基于预设时间一致性的二次控制能够快速准确地完成定时收敛电压的任务要求。相比于传统控制策略,本文所提控制策略具有更实用、更快速的恢复特性,并且克服了微电网初始状态以及设计参数的影响,最后给予实验数据支持,验证所提控制策略的有效性。
本文是基于预设时间一致性的二次调压控制策略,属于虚拟同步发电机控制方案的延伸,为孤岛微电网的二次电压控制提供新型解决方案。但是对于逆变器之间的通讯延迟可能产生的影响,以及负荷波动与电压恢复时间之间的定量关系,本文并未涉及,下一步将会针对以上两方面展开更深入的研究。
参 考 文 献:
[1]WU Heng, RUAN Xinbo, YANG Dongsheng, et al. Small-signal modeling and parameters design for virtual synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4292.
[2]秦本双, 徐永海, 贾焦心. 多VSG功频环路间交互影响的定量分析[J]. 电网技术, 2022, 46(2): 757.
QIN Benshuang, XU Yonghai, JIA Jiaoxin. Quantitative analysis on interactive influences among power-frequency loops of multi-VSG[J]. Power System Technology, 2022, 46(2): 757.
[3]CHENG Huijie, SHUAI Zhikang, SHEN Chao, et al. Transient angle stability of paralleled synchronous and virtual synchronous generators in islanded microgrids[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8751.
[4]ESPINA E, LLANOS J, BURGOS-MELLADO C, et al. Distributed control strategies for microgrids: an overview[J]. IEEE Access, 2020, 8: 193412.
[5]张步云, 王晋宁, 梁定康, 等. 采用一致性算法的自治微电网群分布式储能优化控制策略[J].电网技术,2020,44(5):1705.
ZHANG Buyun, WANG Jinning, LIANG Dingkang,et al. Optimization control strategy of distributed energy storage in autonomous microgrid cluster on consensus algorithm [J]. Power System Technology, 2020, 44(5): 1705.
[6]OLFATI-SABER R, MURRAY R. Consensus problems in networks of agents with switching topology and time-delays [J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520.
[7]CHEN Laijun, WANG Yuyang, YANG Libin, et al. Consensus control strategy with state predictor for virtual synchronous generators in isolated microgrid[C]//2016 IEEE International Conference on Power System Technology (POWERCON), September 28-October 1, 2016, Wollonggong, NSW, Australia. 2016: 1-5.
[8]SIMPSON-PORCO J W, SHAFIEE Q, DORFLER F, et al. Secondary frequency and voltage control of islanded microgrids via distributed averaging[J]. IEEE Transactions on Industrial Electronics, 2015, 62(11): 7025.
[9]LIU Jiayi, LI Jiaqi, SONG Huihui, et al. Nonlinear secondary voltage control of islanded microgrid via distributed consistency[J].IEEE Transactions on Energy Conversion,2020,35(4):1964.
[10]GONG Ping, HAN Qinglong, LAN Weiyao, et al. Finite-time consensus tracking for incommensurate fractional-order nonlinear multiagent systems with directed switching topologies[J]. IEEE Transactions on Cybernetics, 2020, 52(1): 65.
[11]XIAO Feng, WANG Long. Reaching agreement in finite time via continuous local state feedback[C]//2007 Chinese Control Conference,July 26-31,2007,Zhangjiajie,China.2007:711-715.
[12]ZUO Shan, DAVOUDI A, SONG Yongduan, et al. Distributed finite-time voltage and frequency restoration in islanded AC microgrids[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 5988.
[13]马秀娟, 李范, 赵玫, 等. 基于有限时间一致性的微网分布式二次控制[J]. 电机与控制学报, 2021, 25(2): 45.
MA Xiujuan, LI Fan, ZHAO Mei, et al. Distributed finite-time consensus cooperative secondary control of microgrid[J]. Electric Machines and Control, 2021, 25(2): 45.
[14]ZUO Zongyu, HAN Qinglong, NING Boda, et al. An overview of recent advances in fixed-time cooperative control of multiagent systems[J]. IEEE Transactions on Industrial Informatics, 2018, 14(6): 2322.
[15]SARRAFAN N, ROSTAMI M A, ZAREI J, et al. Improved distributed prescribed finite-time secondary control of inverter-based microgrids:design and real-time implementation[J].IEEE Transactions on Industrial Electronics,2021,68(11):11135.
[16]NI Junkang, CAO Hui, LIU Xinghua, et al. Fixed-time leader-follower consensus based secondary voltage control for microgrid under directed communication graph[C]//2021 IEEE International Conference on Real-time Computing and Robotics (RCAR), July 15-19, 2021,Xining,China.2021: 566-571.
[17]NING Boda, JIN Jiong, ZHENG Jinchuan, et al. Finite-time and fixed-time leader-following consensus for multi-agent systems with discontinuous inherent dynamics[J]. International Journal of Control, 2018, 91(6): 1259.
[18]李斌, 周林, 余希瑞, 等. 基于改进虚拟同步发电机算法的微网逆变器二次调频方案[J].电网技术,2017,41(8):2680.
LI Bin, ZHOU Lin, YU Xirui, et al. Secondary frequency regulation for microgrid inverters based on improving virtual synchronous generator [J]. Power System Technology, 2017, 41(8): 2680.
[19]LI Dongdong, ZHU Qianwei, LIN Shunfu, et al. A self-adaptive inertia and damping combination control of VSG to support frequency stability[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 397.
[20]苏晨, 吴在军, 窦晓波. 孤岛微电网分布式P-V协调控制策略[J]. 电力自动化设备, 2021, 41(4): 101.
SU Chen, WU Zaijun, DOU Xiaobo. Distributed P-V coordinated control strategy for islanded microgrid[J]. Electric Power Automation Equipment, 2021, 41(4): 101.
[21]陆瑶, 王杰, 王子强, 等. 基于固定时间一致性算法的孤岛微电网分布式容错二次控制策略[J]. 电力自动化设备, 2022,42(11): 1.
LU Yao, WANG Jie, WANG Ziqiang, et al. Distributed fault-tolerant secondary control strategy for islanded microgrid based on fixed-time consensus algorithm[J]. Electric Power Automation Equipment, 2022, 42(11): 1.
[22]ZUO Zongyu, TIE Lin. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems[J]. International Journal of Systems Science,2014, 47(6): 1366.
[23]NING Boda, HAN Qinglong, ZUO Zongyu, et al. Fixed-time and prescribed-time consensus control of multiagent systems and its applications: a survey of recent trends and methodologies[J].IEEE Transactions on Industrial Informatics,2022,19(2):1121.
(编辑:邱赫男)
