基于奇异摄动的柔性关节机械臂鲁棒控制

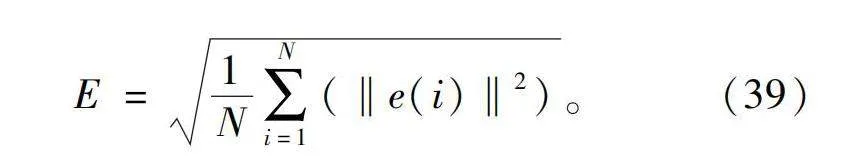
摘 要：针对柔性关节机械臂在扰动过大情况下难以实现高精确度轨迹跟踪的问题，提出一种基于奇异摄动的鲁棒控制方案。该方法不需要对连杆角加速度及其高阶导数进行计算，因此该方法不受高阶导数估计不准确的影响。首先，用奇异摄动法对原系统进行解耦，得到快慢两个异时间尺度的二阶子系统。然后，对慢子系统设计二次补偿控制律，用扰动观测器对扰动进行观测后，进行首次补偿；设计基于Hamilton-Jacobi-Issacs不等式理论的鲁棒控制器进行二次补偿，并证明当扰动有界时，系统跟踪误差将很快收敛于零。最后，对快子系统添加阻尼项，并通过Lyapunov稳定性定理与Lasalle不变性定理证明系统的稳定性。将所提控制方案与反馈线性化方案及奇异摄动PD 控制方案相对比， 结果表明，所提控制方案设计的系统具有较强的抗干扰能力及更好的动态、稳态性能。

关键词：柔性关节；奇异摄动；机械臂；轨迹跟踪；Hamilton-Jacobi-Issacs不等式；鲁棒控制

DOI：10.15938/j.emc.2024.10.018

中图分类号：TH165

文献标志码：A

文章编号：1007-449X（2024）10-0193-08

收稿日期： 2023-01-17

基金项目：国家自然科学基金（12162007）

作者简介：孟范伟（1981—），男，博士，副研究员，研究方向为控制系统的鲁棒设计、非线性控制；

旷 建（1999—），男，硕士， 研究方向为非线性控制、系统建模与仿真；

陈昊男（1999—），男，硕士， 研究方向为控制系统的鲁棒设计、系统建模与仿真；

付中乐（1995—），男，硕士，研究方向为非线性控制。

通信作者：旷 建

Robust control of flexible joint manipulator based on singular perturbation

MENG Fanwei， KUANG Jian， CHEN Haonan， FU Zhongle

（School of Control Engineering， Northeastern University at Qinhuangdao， Qinhuangdao 066004， China）

Abstract：Aiming at the problem that in the flexible joint manipulator it is difficult to achieve high-precision trajectory tracking under the condition of large disturbance， a robust control scheme based on singular perturbation was proposed. This method does not need to calculate the angular acceleration of the connecting rod and its higher-order derivative， so it is not affected by the inaccurate estimation of the higher-order derivative. First， the singular perturbation method was used to decouple the original system， and two second-order subsystems with different time scales were obtained. Then， a multiple compensation control law was designed for the slow subsystem. After the disturbance was observed by the disturbance observer， the first compensation was performed; A robust controller based on Hamilton-Jacobi-Issacs inequality theory was designed for secondary compensation. And it is proved that when the disturbance is bounded， the system tracking error will quickly converge to zero. Finally， the damping term was added to the fast subsystem， and the stability of the system was proved by Lyapunov stability theorem and Lasalle invariance theorem. Comparing the proposed control scheme with the feedback linearization scheme and the singular perturbation PD control scheme， the results show that the system designed by the proposed control scheme has strong anti-interference ability and better dynamic and steady-state performance.

Keywords：flexible joint; singular perturbation; mechanical arm; track tracking; Hamilton-Jacobi-Issacs inequality; robust control

0 引 言

在过去的几十年中， 柔性关节机械臂被应用到各种场景，其轨迹跟踪控制问题也因此受到了广泛的研究^［1］。早期的研究中往往假设机械臂是完全刚性的，针对这一假设，国内外学者提出了多种控制方法，例如直接转矩控制^［2-3］、鲁棒控制^［4］、自适应控制^［5］等。然而，由于关节中存在柔性齿轮、传动带、轴承等能量传递元件，传统的控制方法对于一些刚性轻型机械臂难以获得满意的效果^［6-7］。文献［8］的研究强调了在控制器设计中考虑关节柔性的重要性。文献［9］将柔性元件等效为线性扭转弹簧，提出了柔性关节机械臂数学模型。此后，对柔性关节机械臂控制问题的研究大部分都是基于此模型的。

与刚性模型相比，柔性关节机械臂数学模型微分方程的阶数明显增加，此外机械臂工作环境的外部扰动和建模误差导致控制器设计难度显著增加^［10］。为了提高控制系统的性能，多种方法被应用至柔性关节机械臂的轨迹跟踪控制上，文献［11］提出一种基于扰动观测器的柔性关节机器人PD控制方案，利用扰动观测器消除了扰动的影响并通过实验验证了所设计方案的有效性。文献［12］在考虑输出受限的情况下，设计了一种全状态反馈神经网络控制方案，不仅提升了机器人的安全性，而且提升了控制系统的鲁棒性。文献［13］对两连杆柔性关节机械臂设计了一种滑模变结构控制器，系统状态可以快速到达切换面，并具有较高的控制精确度。文献［14］引入命令滤波器解决了柔性关节机械臂反步控制中对虚拟控制求导时项数爆炸的问题，并证明了闭环跟踪误差系统的稳定性。

跟踪精确度越高的控制系统运行中往往需要越多状态变量反馈，才能获得理想的性能。一般来说， 高阶导数值只能通过连杆角位移测量值多次求导或基于数学模型来计算^［15］。然而，在极端工作环境下，受传感器性能的影响，所获得的反馈量未必准确^［16］，对测量值多次求导则会带来更大的误差。避免求取连杆角位移高阶导数值带来的巨大误差， 奇异摄动法提供了一种理想的解决方案，可以将原系统进行解耦， 得到快慢两个二阶子系统进而分别设计控制器^［17-19］。文献［20］首先设计前馈控制律消除了非线性，然后利用奇异摄动法对柔性关节机械臂模型进行解耦处理，对两个子系统设计了PD控制器，利用劳斯判据证明了控制系统的稳定性并给出选择增益的方法。文献［21］对解耦后的边界层系统设计了增广自适应控制律，仿真结果表明系统可以有效抑制关节振动。然而在深空、深海、深地、极地等极端环境下，柔性关节机械臂受高真空、强辐射、高低温等各种外场及其耦合作用干扰^［22］，这些控制方法显然难以达到理想的效果。为了克服传统控制方案的不足，设计了奇异摄动鲁棒控制的方案。

相比以往的成果，主要创新之处在于：1）设计多次补偿控制律，设计非线性干扰观测器，实现对未知干扰的有效观测，对未知干扰进行首次补偿；2）将全局终端滑模作为Hamilton-Jacobi-Issacs不等式理论的鲁棒控制律的评价函数，设计基于Hamilton-Jacobi-Issacs不等式理论的鲁棒控制器，对扰动进行二次补偿，并证明当扰动有界时，扰动可以很快被补偿。

1 动力学模型

将一个具有柔性关节的连杆机械臂作为被控对象，根据文献［9］所做的研究，同时考虑机械臂工作环境中存在的扰动，可以得到被控对象的动力学模型为：

M（q）q··+C（q，q·）q·+g（q）=K（θ－q）+d₁；（1）

Jθ··+K（θ－q）=u+d₂。（2）

式中：d₁∈Rⁿ和d₂∈Rⁿ分别为连杆侧和电机侧未知外界的集总扰动；q、q·、q··∈Rⁿ分别为连杆角位移、速度和加速度向量；θ、θ·、θ··∈Rⁿ分别为经减速器作用后电机的转子角位移、角速度和角加速度向量；M（q）∈R^n×n为惯性矩阵；C（q，q·）q·∈Rⁿ为机械臂的科氏力和离心力向量；g（q）∈Rⁿ为重力向量；对角正定矩阵K∈R^n×n表示关节刚度；对角矩阵J∈R^n×n为电机惯量矩阵；u为控制器输出向量。

性质1 惯性矩阵M（q）为对称正定矩阵，即满足

性质2 矩阵M·（q）－2C（q，q·）为反对称矩阵，即对于任意向量ξ 满足

ξ^T［M·（q）－2C（q，q·）］ξ=0。（4）

柔性关节机械臂的轨迹跟踪控制问题即初始状态下设计控制律u使q（t）－q_d（t）的值快速收敛至0，实现机械臂在关节空间的轨迹跟踪，其中q_d（t）为连杆角位移q（t）的给定参考角度。

2 二时间尺度分解

首先利用奇异摄动法进行模型解耦，由于机械臂动力学模型中关节刚度矩阵K的元素远远大于模型中其他矩阵的元素，令K-=ε²K，其中ε为奇异摄动参数且满足0lt;εlt;1，定义μ=K（θ－q），则式（1）～式（2）可以写成奇异摄动形式为：

M（q）q··+C（q，q·）q·+g（q）=μ+d₁；（5）

ε²Jμ··+K-μ=K-（u+d₂－Jq··）。（6）

式中：q为慢变量；μ为快变量。令ε=0，此时原系统被降阶成为慢子系统，原系统中的控制输入u变化成为慢子系统控制输入u_s。 μ的近似值即快变量的准稳态为

μ-=u_s+d₂－Jq··。（7）

将式（7）代入式（5）中可得到解耦后的慢子系统为

［M（q）+J］q··+C（q，q·）q·+g（q）=u_s+d₁+d₂。（8）

定义向量y为μ的准稳态μ-的偏差，即y=μ－μ-，将其代入式（6）可得关于y的方程为

ε²J（y··+μ-··）=－K-y+K-u_f。（9）

其中u_f=u－u_s，引入新的时间尺度变量τ并令dτ/dt=1/ε，则式（9）在快时间尺度下可以写为

Jd²ydτ²+Jd²μ-dτ²=－K-y+K-u_f。（10）

在τ时间尺度下，准稳态μ-变化缓慢可视为常数，可令d²μ-/dτ²=0，则式（10）可重新写为

d²ydτ²+J^－1K-y=J^－1K-u_f。（11）

至此得到两个二阶子系统，其运动方程分别为式（8）和式（11），原系统的控制律为两个子系统控制律之和，即μ=μ_s+μ_f，通过对μ_s和μ_f分别设计，使原系统的复合控制律仅需连杆角位移和速度反馈成为可能。

3 控制系统设计

控制系统框图如图1所示。

3.1 慢子系统设计

利用奇异摄动法已得到慢子系统式（8），该子系统的控制器设计目标为使q与参考角度q_d的偏差e=q－q_d快速收敛至0。令系统的总扰动d=d₁+d₂，D（q）=M（q）+J，慢子系统可重新写为

D（q）q··+C（q，q·）q·+g（q）=u_s+d。（12）

扰动的存在将影响轨迹跟踪性能，为了提高控制系统抗扰动能力，首先设计扰动观测器得到复合扰动的估计值并将其应用于控制律中补偿原扰动，观测器设计为：

式中：ω为辅助变量；d^为扰动d的估计值；N为待设计的常数可逆正定矩阵。

定理1 假设扰动的变化速率与式（13）中其他变量相比可忽略不计，令d·=0，扰动估计值d^可收敛至d的充分条件为N满足矩阵不等式

N+N^T－N^TD·（q）N≥0。（14）

注：对于任意矩阵A，A≥0指矩阵A为半正定矩阵。

证明：由式（13）对扰动估计值d^求导得

令扰动观测偏差d～=d^－d，由于假设d·=0，所以有d^·=d～·，代入式（15）可得

d～·=－N^－1D^－1（q）d～。（16）

定义Lyapunov函数为

V_d=d～^TN^TD（q）Nd～=（Nd～）^TD（q）（Nd～）。（17）

由于D（q）=M（q）+J且M（q）和J均为对称正定矩阵，所以D（q）也为正定矩阵，有V_d≥0。

对V_d求导得

由式（18）可得，当N+N^T－N^TD·（q）N≥0时，有V·_d≤0，进而得到扰动观测值d^可收敛至机械臂慢子系统的实际扰动d，证毕。

对慢子系统设计复合控制律u_s=u_s1+u_s2，利用扰动观测值d^和机械臂参考角度轨迹q_d以及实际的连杆角位移q设计u_s1为

u_s1=D（q）q··_d+C（q，q·）q·_d－d^。（19）

式中d～可视为补偿后新的扰动信号。将其代入式（12）可得到以轨迹跟踪偏差为状态变量的运动方程为

D（q）e··+C（q，q·）e·+g（q）+d～=u_s2。（20）

对于向量a=［a₁ a₂ … a_n］^T∈Rⁿ和常数b，定义a^b=［a^b₁ a^b₂ … a^b_n］^T，为了使系统稳定且具有较强的鲁棒性，定义系统式（19）的评价信号为

η=e·+αe+βe^m/n。（21）

式中：矩阵α=diag［α₁，α₂，…，α_i，…，α_n］，α_igt;0；矩阵β=diag［β₁，β₂，…，β_i，…，β_n］，β_igt;0；m和n均为正奇数，且ngt;m。则当设计控制律使‖η‖收敛至0时，偏差‖e‖也在有限时间内快速收敛至0。

在d～存在的情况下，‖η‖的值越小意味着系统的抗扰动能力越强，定义鲁棒性能指标信号为

σ=sup‖d～‖≠0‖η‖₂‖d～‖₂。（22）

式中‖η‖₂=（∫^∞₀η^Tηdt）^0.5。

引理1 （Hamilton-Jacobi-Issacs不等式理论^［23］）对于任意小的正数χ，式（22）中的鲁棒性能指标σ≤χ的充分条件为存在光滑函数V≥0满足

V·≤12χ²‖d～‖²－12‖η‖²。（23）

慢子系统复合控制律中的u_s2设计为

u_s2=－Dαe·－Cαe+g（q）－（12χ²+12）η－

mnDβdiag（e^m/n－1_i）e·－Cβe^m/n。（24）

定理2 当系统式（20）中的控制律u_s2为式（24）时，该系统定义为式（22）的鲁棒性能指标σ可以小于等于任意正数λ。

证明：对评价信号式（21）求导得

η·=e··+αe·+mnβdiag（e^m/n－1_i）e·。（25）

同时代入式（20）可得

将式（24）的控制律代入可得

Dη·=－Cη－d～－（12χ²+12）η。（27）

定义函数V为

V=12η^TDη。（28）

对其求导得

V·=12η·^TDη+12η^TD·η+12η^TDη·=η^TDη·+

12η^TD·η=η^T（－12χ²η－12η－d～）+

12η^T（D·－2C）η。（29）

由于D=M+J，且矩阵J为常数矩阵，所以有D·=M·，根据柔性关节机械臂的性质2可得η^T（D·－2C）η=0，则式（29）可进一步化简为

V·=－12χ²η^Tη－12η^Tη－η^Td～。（30）

令I=0.5χ²‖d～‖²－0.5‖η‖²，则可以得到

V·－I=－12χ²η^Tη－12η^Tη－η^Td～－12χ²‖d～‖²+

12‖η‖²=－12（1χ²η^Tη+2η^Td～+

χ²‖d～‖²）=－121χη+χd～²。（31）

由上式可得V·－I≤0，即V·≤0.5χ²‖d～‖²－0.5‖η‖²。

根据引理1可知定理2得证。

3.2 快子系统设计

前文已利用奇异摄动法解耦得到快子系统方程为

d²ydτ²+J^－1K-y=J^－1K-u_f。（32）

该系统为二阶非线性无阻尼系统，在控制律u_f 中加入阻尼项，设计控制律为

u_f=－εK-^－1K₁μ·=－K-^－1K₁dμdτ。（33）

式中K₁为对角正定系数矩阵。

在快子系统τ时间尺度下，准稳态μ-相对其他变量变化缓慢可视为常量且y=μ－μ-，控制律式（33）可重新写为

u_f=－K-^－1K₁dydτ。（34）

将控制律代入式（32）可得

d²ydτ²+J^－1K₁dydτ+J^－1K-y=0。（35）

定义Lyapunov函数为

V_f=12y^′Ty^′+12y^TJ^－1K-y。（36）

式中y^′=dy/dτ，另外在快时间尺度下，慢变量q变化缓慢可视为常量，所以可令（M^－1）^′=0，对Lyapunov函数在时间尺度求导得

dV_fdτ=12y^″Ty^′+12y^′Ty^″+12y^′TJ^－1K-y+

12y^TJ^－1K-y^′+12y^T（J^－1K-）^′y=y^′Ty^″+

y^′TJ^－1K-y=y^′T（－J^－1K-y－J^－1K₁y^′）+

y^′TJ^－1K-y=－y^′TJ^－1K₁y^′。（37）

由于矩阵J^－1、K₁和M^－1均为正定矩阵，所以有V_fgt;0，dV_f/dτ≤0，当V^′_f≡0时，y^′=0，根据Lasalle不变性定理^［24］，当选择合适的增益时边界层系统是稳定的，证毕。

连立式（19）、式（24）、式（34）可得复合控制器为

u=u_s+u_f=D（q）q··_d+C（q，q·）q·_d－d^－

Dαe·－Cαe+g（q）－（12χ²+12）η－

mnDβdiag（e^m/n－1_i）e·－Cβe^m/n－K-^－1K₁εμ·。（38）

4 仿真分析

以图2所示的双连杆柔性关节机械臂作为被控对象进行计算机仿真分析。

动力学模型式（1）～式（2）中的参数矩阵分别为：

M（q）=n₁+n₂+2n₃cosq₂n₂+n₃cosq₂n₂+n₃cosq₂n₂；

C（q，q·）=－n₃q·₂sinq₂－n₃（q·₁+q·₂）sinq₂n₃q·₁sinq₂0；

G（q）=n₄gcosq₁+n₅gcos（q₁+q₂）n₅gcos（q₁+q₂）。

式中：q=［q₁q₂］^T；n₁=（m₁+m₂）l²₁；n₂=m₂l²₂；n₃=m₂l₁l₂；n₄=（m₁+m₂）l₁；n₅=m₂l₂。机械臂固有参数的设置如表1所示，关节刚度矩阵和电机惯量矩阵分别为：

K=10 0000010 000；J=1.3001.3。

表1中连杆2的质量包括抓取物品的质量及连杆2的本身质量。首先设置所设计的控制器输出u=u_s+u_f中的参数，令奇异摄动参数ε=0.1，通过试错法，得到准稳态系统所设计的控制律u_s中α=diag（3，3），β=diag（0.3，0.1），m=3，n=5，χ=0.035。在快子系统即边界层系统中所设计的控制律u_f中，K₁=diag（100，570），系统的输出即连杆的初始位置设定为q=［0 0］^T。

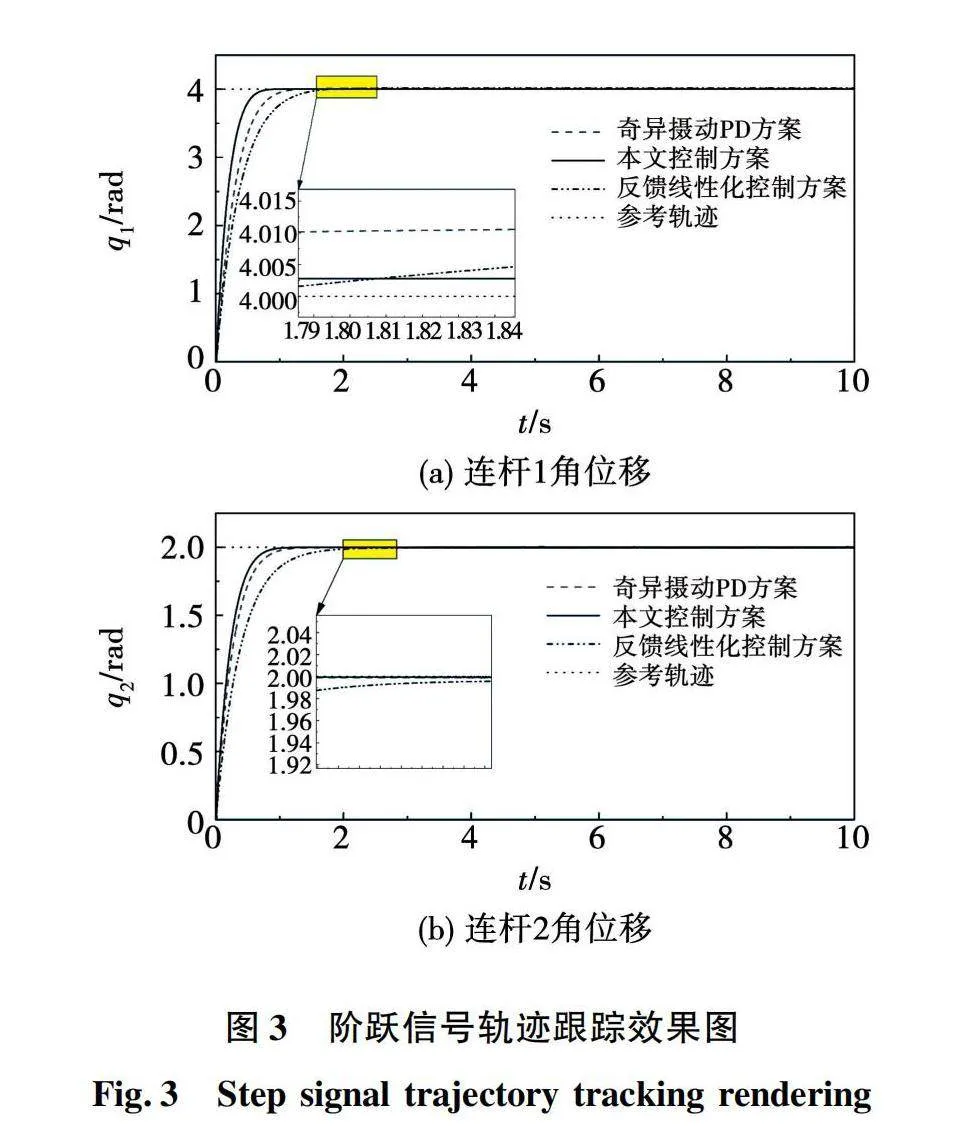
为了验证所提控制方案在柔性关节机械臂的轨迹跟踪控制中具有更好的效果，将奇异摄动PD控制器与反馈线性化控制方案参数调到最佳与所提出方案作对比。在忽略外界扰动的情况下，令连杆1和连杆2的参考轨迹都为阶跃信号，两连杆的轨迹跟踪曲线如图3所示。

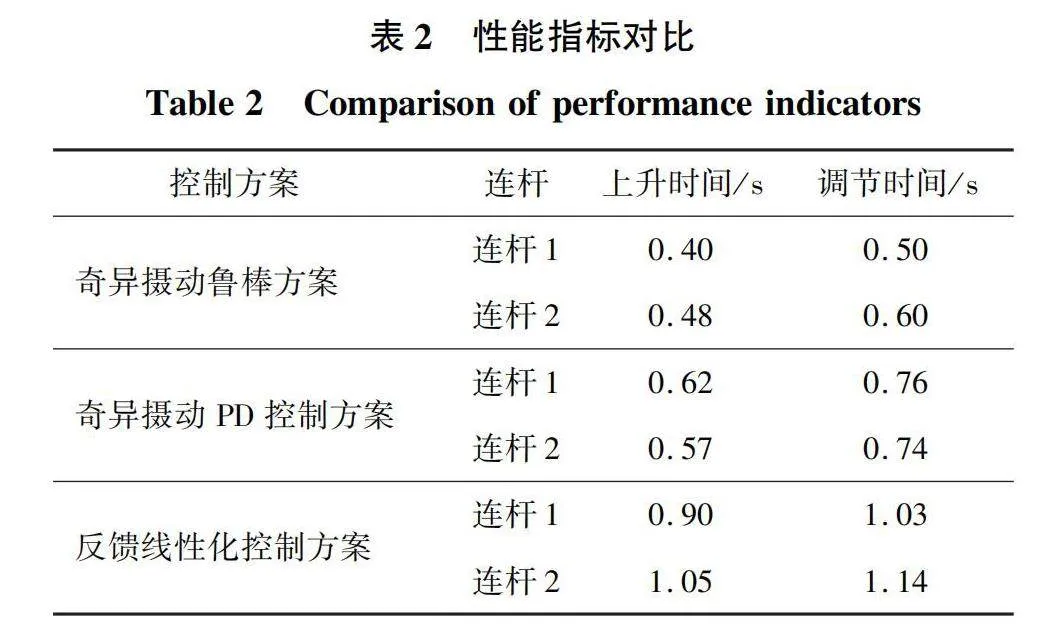
为了更加直观地比较两种控制方案对双连杆柔性关节机械臂的轨迹跟踪性能，分别计算出3种控制方案的上升时间、调节时间，经计算后的实际值如表2所示。

由表2可知，相比传统的奇异摄动PD控制方案与反馈线性化控制方案，所设计的奇异摄动鲁棒控制方案上升时间和调节时间都明显更小，具有更良好的瞬态性能，输出角位移可以更快的跟踪上参考轨迹。

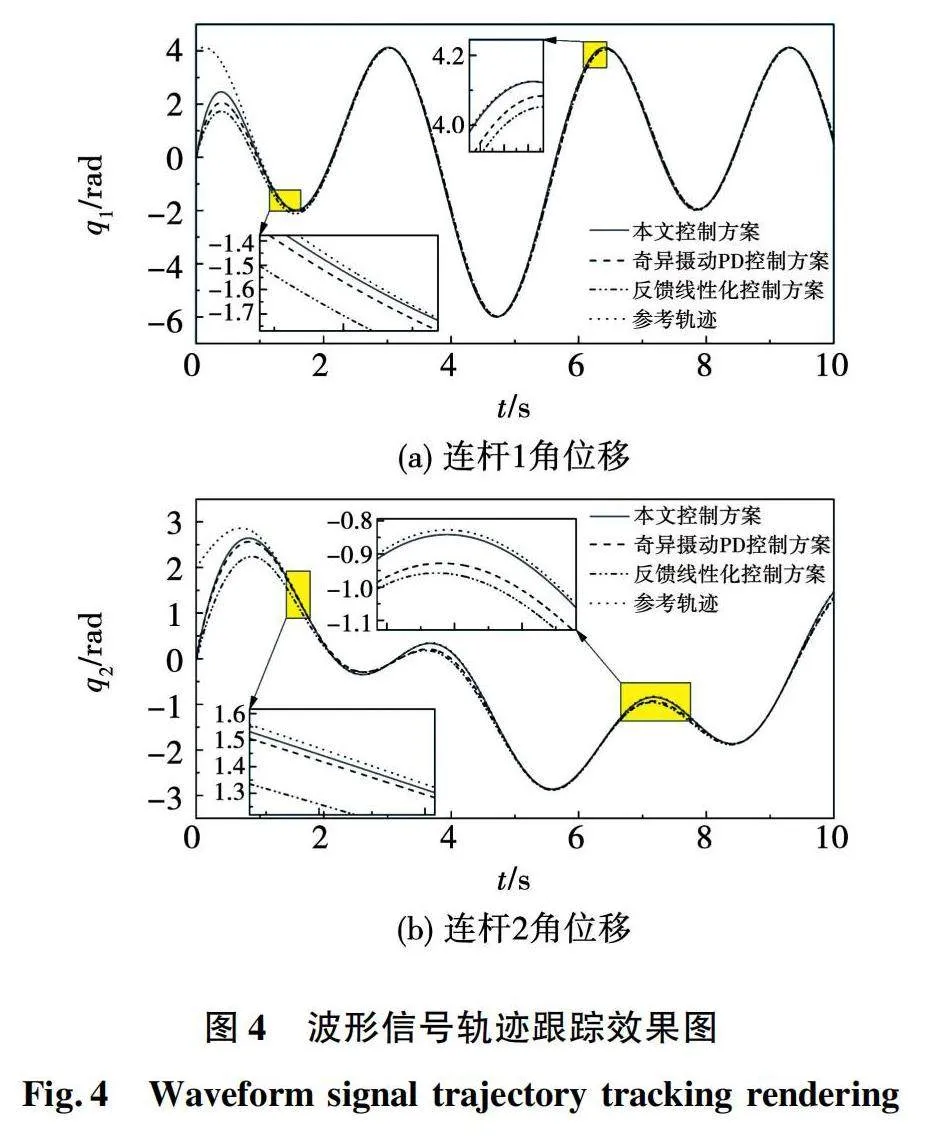
为了验证所设计控制方案在控制系统中存在未知外界扰动的情况下，能够克服扰动的影响并实现机械臂的轨迹跟踪，加入扰动信号d₁=［3+5q·₁+10q₁，3+5q·₂+10q₂］，d₂=［4+5q·₁+10q₁，4+5q·₂+10q₂］，连杆1的参考轨迹为q_1d=2sin（t）+4cos（2t），连杆2的参考轨迹为q_2d=sin（2t）+2cos（0.5t），输出即连杆的初始位置设定为q=［0 0］^T。同时与奇异摄动PD控制方案及反馈线性化控制方案对比，双连杆的轨迹跟踪效果如图4所示。

如图4所示，与奇异摄动PD控制方案及反馈线性化控制方案相比，当加入扰动时，3种控制方案的跟踪性能展现出差距，所设计的奇异摄动鲁棒控制方案的轨迹跟踪性能明显优于其余两种控制方案，暂态性能也就是连杆角位移由0上升到参考轨迹的速度也明显快于奇异摄动PD控制方案与反馈线性化控制方案。

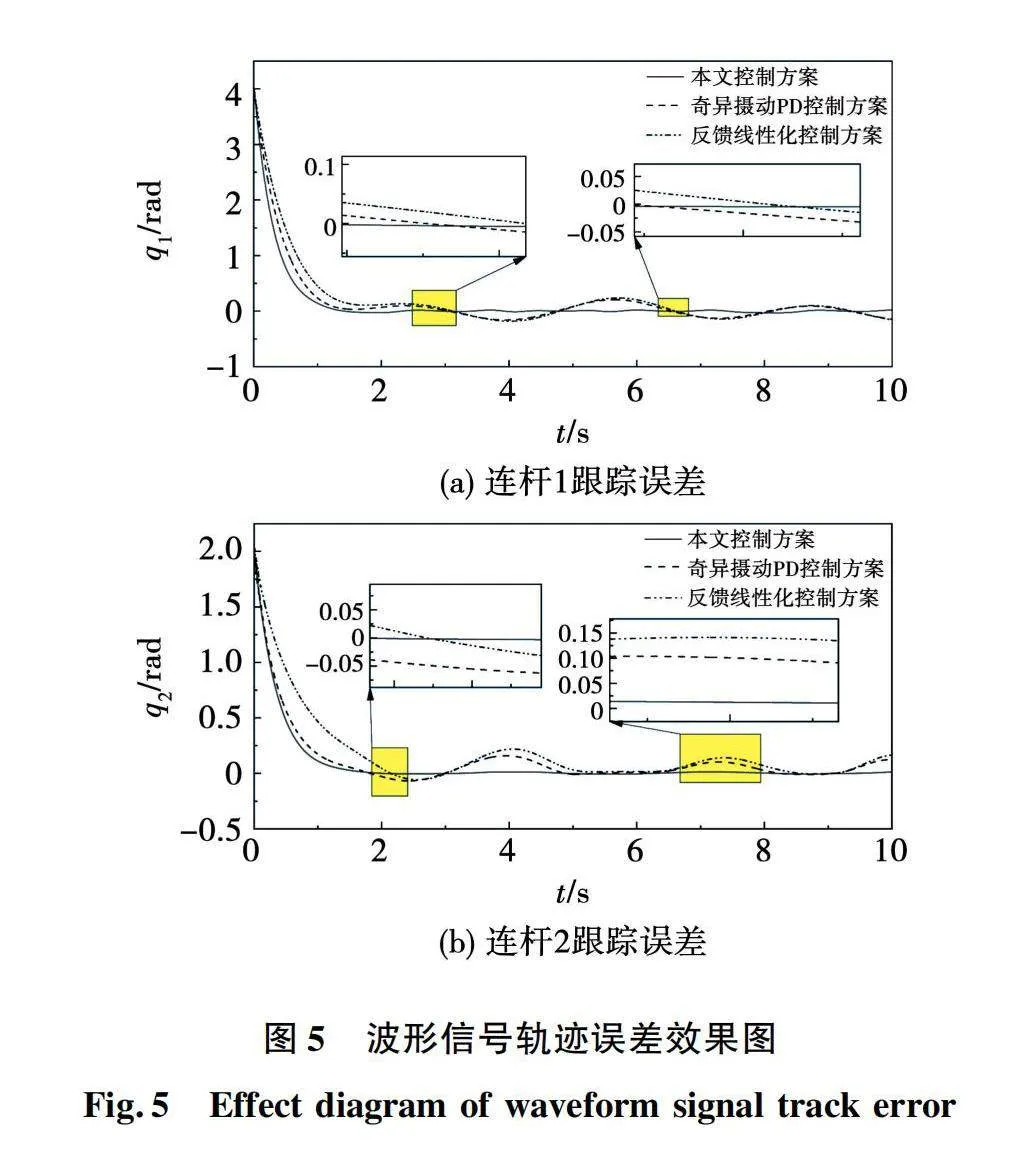
两种控制方案的轨迹跟踪误差如图5所示。

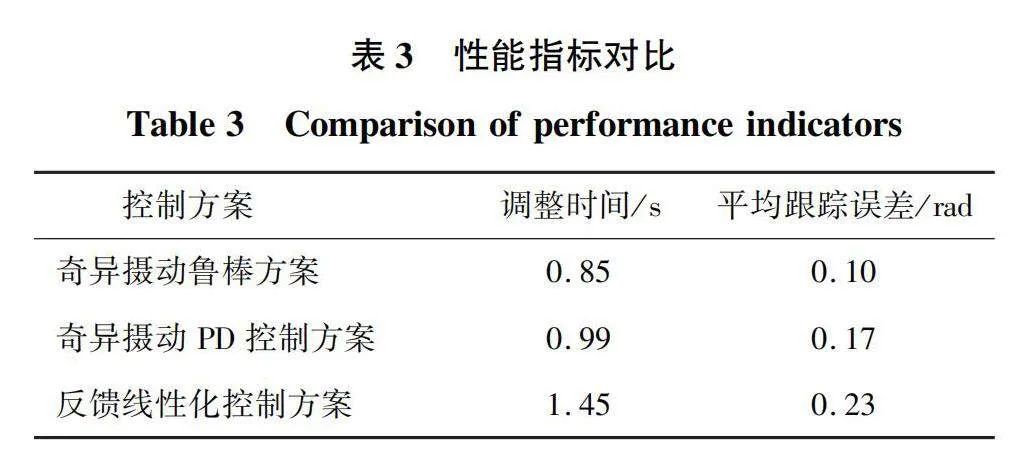
为了更直观比较这3种具有抗扰动能力控制律的性能，计算出采用每一种控制律的系统在连杆1和连杆2的平均调整时间（输出角位移上升并保持与参考轨迹角位移偏差小于0.15 rad的时间）和平均跟踪误差E，E的定义为

E=1N∑Ni=1（‖e（i）‖²）。（39）

式中N为采样次数，取为100 000，两种控制方案的性能指标对比如表3所示。

与奇异摄动PD控制方案及反馈线性化控制方案相比，所设计的鲁棒控制方案由于设计了合适形式的评价信号，设计控制律时也依照较高的性能指标，保证了所设计控制律具有更快的收敛速度和更小的稳态误差，具有较高的轨迹跟踪精确度。

5 结 论

针对柔性关节机械臂受大干扰影响难以高精确度进行轨迹跟踪的问题，提出一种奇异摄动鲁棒控制方案，利用奇异摄动法将柔性关节机械臂控制系统解耦为两个二阶系统， 降低了设计难度， 减少了计算量。对慢子系统设计了二次补偿控制律，设计干扰观测器观测干扰，对干扰进行首次补偿；设计了基于Hamilton-Jacobi-Issacs不等式的鲁棒控制律进行二次补偿，并证明了当扰动有界时，扰动可以很快被补偿，边界层子系统加入阻尼控制量使其稳定， 并通过Lyapunov稳定性定理与Lasalle不变性定理证明了系统的稳定性。仿真分析结果表明，控制系统可以使双连杆柔性关节机械臂有效跟踪参考轨迹， 具有良好的跟踪性能和抗干扰能力， 可以很好地适用于一些干扰巨大的工作环境。

参 考 文 献：

［1］OZGOLI S， TAGHIRAD H D. A survey on the control of flexible joint robots［J］. Asian Journal of Control， 2006， 8（4）： 332.

［2］GARCIA E， JIMENEZ M A， DE SANTOS P G， et al. The evolution of robotics research［J］. IEEE Robotics amp; Automation Magazine， 2007， 14（1）： 90.

［3］KAGAYA K， PATEK S N. Feed-forward motor control of ultrafast， ballistic movements［J］. Journal of Experimental Biology， 2016， 219（3）： 319.

［4］秦化淑，李树荣，程代展.刚性机械臂跟踪控制的鲁棒控制器设计［J］.控制与决策， 1991， 1（1）： 14.

QIN Huashu， LI Shurong， CHENG Daizhan. Design of robust controller for tracking control of rigid manipulator ［J］. Control and Decision， 1991， 1（1）： 14.

［5］AMBROSINO G， CELENTANO G， GAROFALO F. Robust model tracking control for a class of nonlinear plants［J］. IEEE Transactions on Automatic Control， 1985， 30（3）： 275.

｛6｝ SAYAHKARAJY M， MOHAMED Z， MOHD FAUDZI A A. Review of modelling and control of flexible-link manipulators［J］. Proceedings of the Institution of Mechanical Engineers， Part I： Journal of Systems and Control Engineering， 2016， 230（8）： 861.

［7］孟范伟，何朕，王广雄，等.挠性系统的控制设计和H∞回路成形法［J］. 控制理论与用， 2013， 30（8）： 1014.

MENG Fanwei， HE Zhen， WANG Guangxiong， et al. Control design of flexible systems and H∞ loop shaping method［J］. Control theory amp; Application， 2013， 30（8）： 1014.

［8］SWEET L， GOOD M. Redefinition of the robot motion-control problem［J］. IEEE Control Systems Magazine， 1985， 5（3）： 18.

［9］SPONG M W. Modeling and control of elastic joint robots［J］.Mathematical and Computer Modelling，1989，12（7）：912.

［10］KIM J. Two-time scale control of flexible joint robots with an improved slow model［J］. IEEE Transactions on Industrial Electronscs， 2017， 65（4）： 3317.

［11］KIM M J， CHUNG W K. Disturbance-observer-based PD control of flexible joint robots for asymptotic convergence［J］. IEEE Transactions on Robotics， 2015， 31（6）： 1508.

［12］HE W， YAN Z， SUN Y， et al. Neural-leaming-based control for a constrained robotic manipulator with flexible joints［J］. IEEE Transactions on Neural Ner-works amp; Leaning Systems， 2018， 29（12）：5993.

［13］汪允鹤， 李宏胜， 张伟. 柔性关节机械臂的滑模变结构控制［J］. 组合机床与自动化加工技术， 2017（10）： 91.

WANG Yunhe， LI Hongsheng， ZHANG Wei. Sliding mode variable structure control of flexible jointmanipulator ［J］. Modular Machine Tools and Automatic Processing Technology， 2017（10）： 91.

［14］李鹏飞， 张银河， 张蕾， 等. 考虑误差补偿的柔性关节机械臂命令滤波反步控制［J］.控制理论与应用，2020，37（8）：24.

LI Pengfei， ZHANG Yinhe， ZHANG Lei， et al. Command filtering backstepping control of flexible joint manipulator considering error compensation［J］. Control Theory amp; Application， 2020， 37（8）： 24.

［15］TADOLE S E， KOLHE J P， PHADKE S B. Extended-stale-observer-based control of flexible-joint system with experimental validaition［J］. IEEE Transactions on Inductrial Electronics， 2009， 57（4）： 1411.

［16］刘福才， 闫莉莉， 秦利， 等. 变负载空间机械臂混沌运动分析与控制［J］. 电机与控制学报， 2019， 23（10）：120.

LIU Fucai， YAN Lili， QIN Li， et al. Chaotic motion analysis and control of space manipulators with variable loads［J］. Electric Machines and Control， 2019， 23（10）： 120.

［17］刘华山， 朱世强， 王宣银. 扭矩输入有界的机器人模糊PD轨迹跟踪［J］. 电机与控制学报， 2010， 14（1）： 78.

LIU Huashan， ZHU Shiqiang， WANG Xuanyin. Rajectory racking control for robot manipulators with bnounded torque inputs via fuzzy PD［J］.Electric Machines and Control，2010，14（1）：78.

［18］KHAH H K. GRIZZLE J W. Nonlinear systems upper saddle river［M］. Premtice Hall， 2002.

［19］刘福才，刘林， 徐智霸. 柔性关节空间机械臂奇异摄动模糊PID控制仿真研究［J］. 高技术通讯， 2019， 29（7）： 661.

LIU Fucai， LIU Lin， XU Zhiba. Simulation study on singular perturbation fuzzy PID control of flexible joint space manipulator［J］. High Technology Communication， 2019， 29（7）： 661.

［20］KIM J， CROFT E A. Full-state tracking control for flexible joint robots with singular perturbation techniques［J］. IEEE Transactions on Control Systems Technology， 2019， 27（1）： 63.

［21］陈志勇， 陈力. 带有柔性补偿的柔性关节空间机嚣人的增广自适应控制及关节振动抑制［J］. 宇航学报， 2013， 34（12）： 1599.

CHEN Zhiyong， CHEN Li. Augmented adaptive control and joint vibration suppression of flexible joint space robot with flexible compensation［J］. Astronautica Sinica， 2013， 34（12）： 1599.

［22］常可可， 陈雷雷， 周若男， 等. 极端环境表面工程及其共性科学问题研究进展［J］.中国机械工程，2022，33（12）：1388.

CHANG Keke， CHEN Leilei， ZHOU Ruonan， et al. Research progress of extreme environment surface engineering and its common scientific problems［J］.China Mechanical Engineering， 2022， 33（12）： 1388.

［23］WANG Y N， SUN W， XIANG Y Q， et al. Neural network-based robust tracking control for robots［J］. Intelligent Automation and Soft Computing， 2009， 15（2）： 211.

［24］ZHAO B， XIAN B. Nonlinear robust adaptive tracking control of a quadrotor UAV via immersionand invariance methodology［J］. IEEE Transactions on Industrial Electronics，2015，62（5）：2891.

（编辑：邱赫男）