基于优化粒子群算法的微纳卫星电机参数整定
2024-12-03周航王昊金仲和
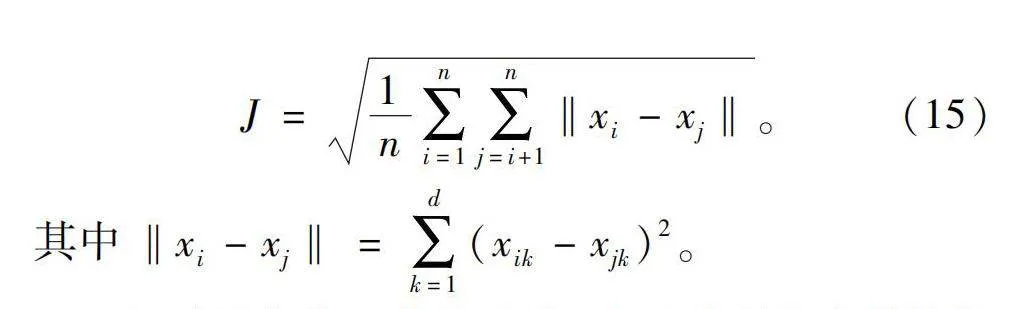
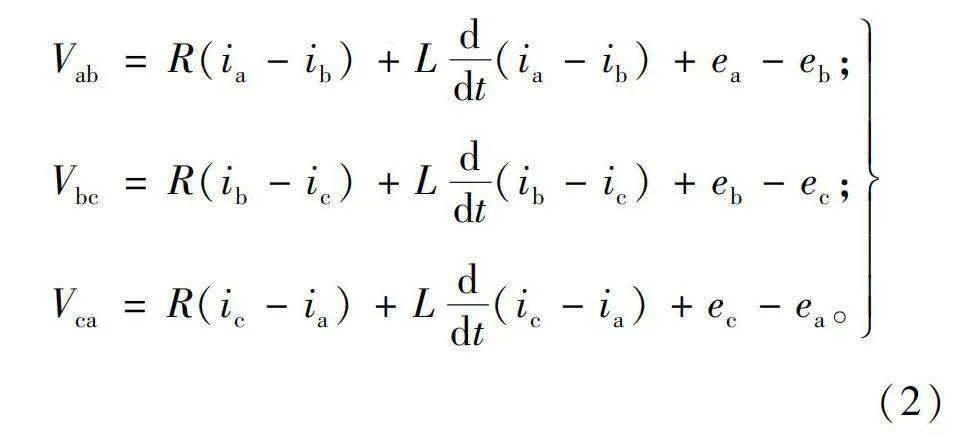
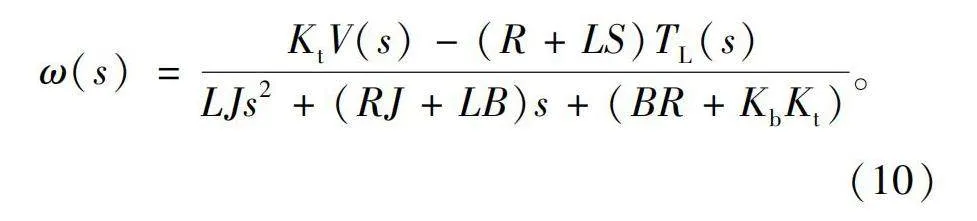
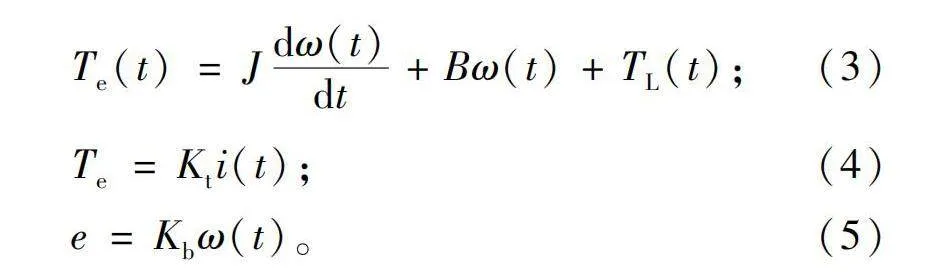
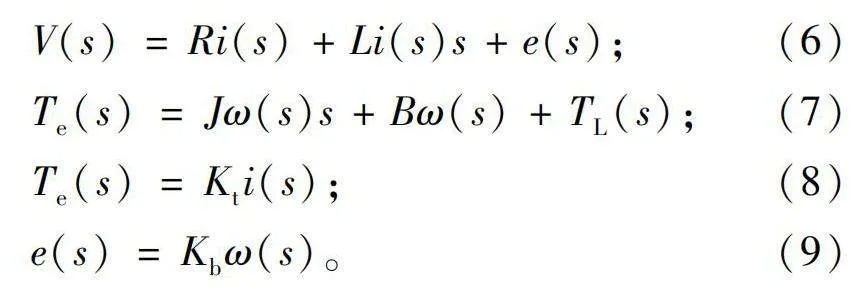

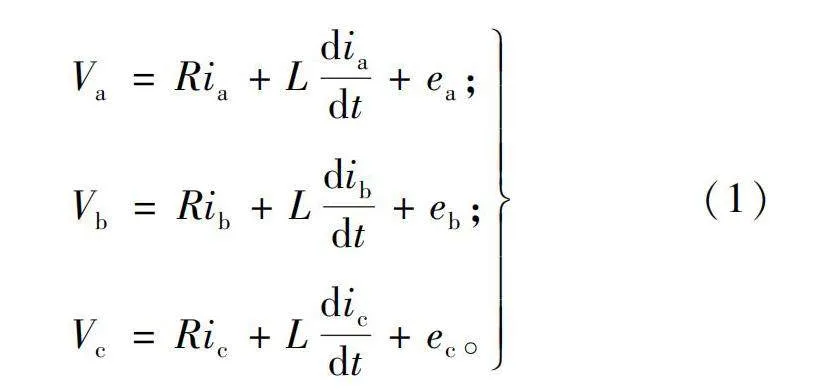
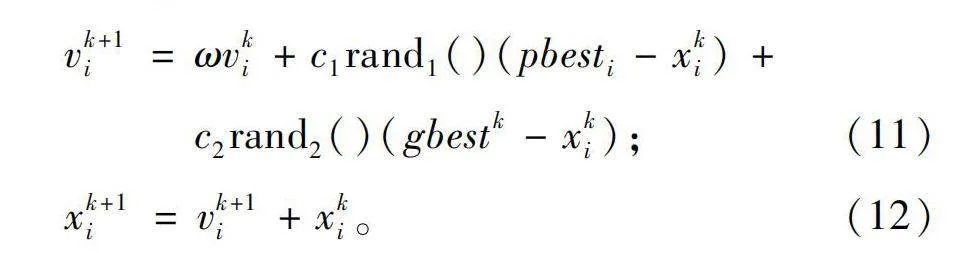
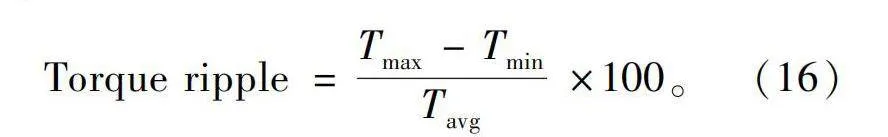
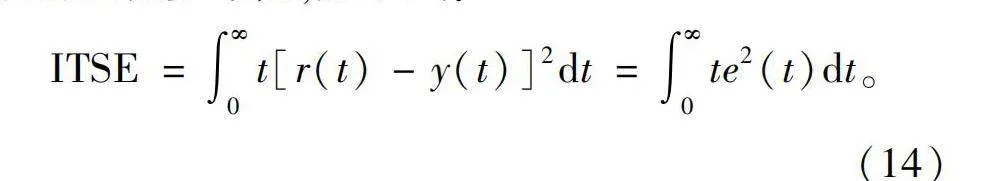
摘 要:针对传统PID控制器控制无刷电机时系统响应慢、速度波动大的问题,以及手动整定大规模电机参数繁琐重复的问题,采用了一种基于粒子群优化算法的无刷直流电机PID参数整定方法,用于确定电机闭环控制系统中PI控制器的参数。首先建立磁场定向控制技术驱动的无刷直流电机控制系统仿真模型,然后在此模型上应用优化粒子群算法进行参数整定优化的迭代过程,得到整定后的控制器参数结果。分析优化粒子群算法整定后的电机速度响应和力矩输出情况,并与传统手动整定结果和其他算法的整定结果进行对比。实验结果表明,提出的优化粒子群算法整定的控制器速度响应更快并且输出力矩更稳定,并且对电机参数的小幅度变化有鲁棒性,该方法可以适用于大规模同类别同批次的电机控制器参数标定。
关键词:微纳卫星;控制系统;无刷直流电机;PID控制;参数整定;粒子群算法
DOI:10.15938/j.emc.2024.10.002
中图分类号:TM33
文献标志码:A
文章编号:1007-449X(2024)10-0013-11
收稿日期: 2024-04-16
作者简介:周 航(2000—),男,硕士研究生,研究方向为电机控制、嵌入式技术;
王 昊(1974—),男,博士,副教授,博士生导师,研究方向为微小卫星姿态控制系统、星载新型传感器及执行器;
金仲和(1970—),男,博士,教授,博士生导师,研究方向为微小卫星、微机电系统等。
通信作者:王 昊
Parameter tuning of micro-satellite motor based on optimized particle swarm optimization algorithm
ZHOU Hang1,2, WANG Hao1,2,3, JIN Zhonghe1,2,3
(1.Micro-Satellite Research Center, Zhejiang University, Hangzhou 310058, China; 2.Huanjiang Laboratory, Zhuji 311800, China; 3.Key Laboratory of Micro-Nano Satellite Research Zhejiang Province, Hangzhou 310058, China)
Abstract:In order to solve the problem of slow response and large speed fluctuation when the traditional PID controller controls the brushless motor, and to solve the problem of tedious and repetitive manual tuning of large-scale motor parameters, a PID parameter tuning method was adopted based on particle swarm optimization algorithm to determine the parameters of PI controller in the motor closed-loop control system. Firstly, the simulation model of brushless DC motor control system was established driven by field oriented control technology, and the optimization particle swarm optimization algorithm was applied to the model to carry out the iterative process of parameter tuning optimization, finally a set of controller parameter results were got. The speed response and torque output of the motor were analyzed after PSO tuning, and the results were compared with those of traditional manual tuning and other algorithms tuning. The experimental results show that the proposed optimized particle swarm optimization algorithm tuning controller has faster speed response and more stable output torque, and is robust to small changes of motor parameters. The method can be applied to large-scale motor controller parameter calibration of the same class and batch.
Keywords:micro satellites; control systems; brushless DC motors; PID control; parameter tuning; particle swarm optimization
0 引 言
随着芯片、微机电系统(micro-electro-mechanical system,MEMS)等技术的不断发展,电子系统的功耗和规模都在不断缩小,同时带来卫星体积的缩小。微纳卫星低成本、短周期、快速交付的特点有助于卫星的商业化进程,同时规避大型卫星的巨大风险[1]。
卫星姿控系统作为微纳卫星最重要的子系统之一,主要由动量轮组、磁力矩器和太阳敏感器等传感器组成,其中动量轮组通过电机带动负载的质量块提供力矩输出来实现卫星的姿态控制。无刷直流电机(brushless DC motor,BLDC)以高效率、良好的控制性、耐用性以及电气噪音小等优点被广泛用于工业中。因此,对BLDC的控制研究热度居高不下,近年来研究者广泛提出了非线性控制、最优控制、自适应控制等控制方法。然而上述控制方法存在理论复杂或实现困难的问题,所以PID控制至今仍是实用性最强,普适性最好的控制方法。目前可以通过一些方法优化PID控制器或者基于规则整定控制器参数[2-3],从而使整个系统具有更好的性能。在过去的几年中,许多研究者也使用人工智能算法对PID参数进行整定以实现更好的性能,例如蜂群算法[4]、和谐搜索[5]、遗传算法[6]、模拟退火算法[7]、粒子群优化算法[8]、细菌觅食算法[9]等。
Ensi和Enim等[10]采用多目标蚁群优化方法对PID控制器进行整定,通过误差最小化目标函数来调整PID控制器的最优解,结果表明该优化方法与经典方法和遗传算法相比具有更好的控制系统性能。
Jun Shi等[11]提出了PF-PI控制器,该方法是基于粒子群算法和模糊逻辑控制来优化PI控制器。在传统的无刷电机控制基础上,改进了PI控制器的结构和电机速度闭环系统的动态性能。
Smail Bazi等[12]提出了一种快速萤火虫算法(fast firefly algorithm,FFA)来确定PID参数的最优值,并与标准萤火虫算法进行比较,并在文中给出了通过FFA方法优化PI控制器参数来控制BLDC的应用。
Tingting Wang等[13]提出一种使用双模糊逻辑系统(dnal fuzzy logic system,FLS)和和谐搜索算法(harmony search algorithm,HAS)优化PID的方法,通过MATLAB仿真进行实验分析,验证了其优越性和稳定性。
Ridwan等[8]实现了一种基于粒子群优化算法的控制器,考虑响应速度,误差等指标,基于粒子群算法优化PID控制参数,结果表明所设计的PSO-PID控制器应用在BLDC上有更好的响应速度和更小的超调量和误差。
Mohammad等[14]在PSO算法优化PID参数的基础上,使用Ziegler-Nichols方法将Kp、Ki、Kd 3个参数变成2个参数,使得PSO的搜索维度下降,缩短了计算时间并使结果更加准确。文中仿真结果表明,所提出的基于粒子群优化的ziegler-nichols方法的PID控制(particle swarm optimization based ziegler-nichols method for PID control,PID-PSO-ZN)算法能够精确地确定最佳PID参数,从而减少系统响应的上升时间和超调量。
本文采用优化粒子群算法对无刷电机控制系统的PI参数进行整定,以电机的速度响应和力矩输出为指标,尝试用一种自动化的方法找到电机控制系统中PI控制器的最优解。介绍BLDC的数学模型以及电机闭环控制系统的特征方程,简述粒子群优化算法,介绍如何将优化PSO算法与PID控制器结合,利用Simulink对电机闭环控制系统进行仿真实验,并分析电机的速度响应和力矩输出在不同情况的表现。
1 无刷直流电机建模
无刷直流电机通常有三相定子绕组。每相的电压方程表述如下:
其中:V为电机每相的电压;R为相电阻(假设三相电阻相同);L为每相电感(假设三相电感相同);e为反电动势;i为相电流。此处忽略各相互感的影响。
由式(1)的相电压两两相减得到线电压:
无刷电机的运动学方程表示如下:
Te=Kti(t);(4)
e=Kbω(t)。(5)
式(3)中:Te为电机的电动扭矩;J为转动惯量;B为阻尼系数;TL为电机上的负载扭矩。式(4)表示电机转矩和电流线性相关,Kt为电机扭矩系数。式(5)中:e为反电动势;Kb为反电动势常数。
将式(1)、式(3)~式(5)进行拉普拉斯变换得到:
V(s)=Ri(s)+Li(s)s+e(s);(6)
Te(s)=Jω(s)s+Bω(s)+TL(s);(7)
Te(s)=Kti(s);(8)
e(s)=Kbω(s)。(9)
根据式(6)~式(9)可以推导出受输入电压和负载转矩影响的响应速度为
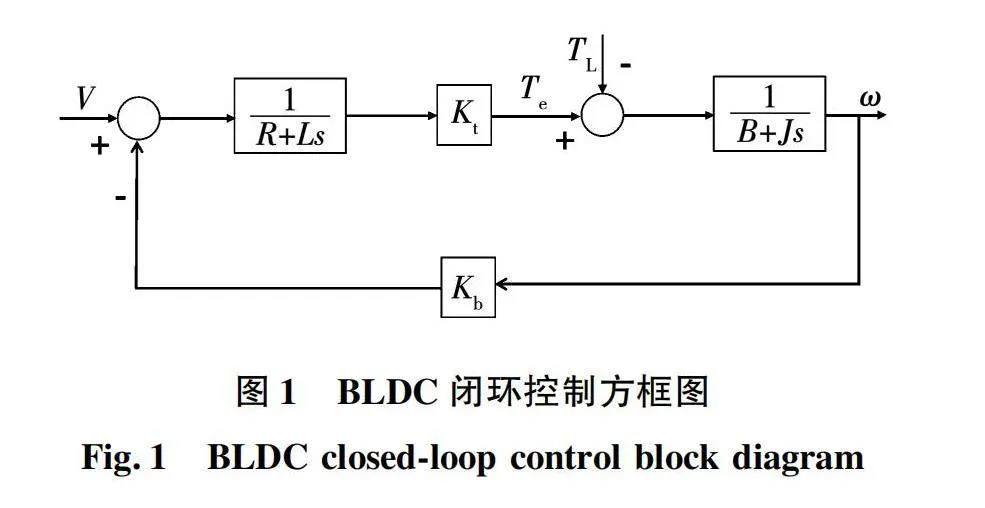
根据式(10)得到 BLDC的闭环控制框图如图1所示,在后续的建模和实验中,也将采用双闭环的控制系统,电流环为内环,速度环为外环,实现对电机转速和力矩的控制。
2 粒子群优化算法
2.1 粒子群优化算法简述
粒子群算法(particle swarm optimization,PSO)是一种受群体运动启发的智能算法,最早由KENNEDY J和EBERHART R C提出[15],经过不断改进变化最终形成了粒子群优化算法,也有简称为粒子群算法。
PSO算法的思想来自于自然界群体觅食的行为。在群体寻找食物的过程中,每个个体按照各自随机的方向搜索,在搜索过程中记录自己找到最佳位置,同时群体中的每个个体也会共享自己找到最佳位置,因此对于个体而言,搜索方向收到自身历史的搜索结果和群体中其他个体搜索结果的共同影响。PSO算法被常用来寻找一定区域中函数的最值。
在PSO算法中,每个个体被称为粒子,每个粒子在D维空间中运动。初始时刻每个粒子随机均匀分布在有限空间中,并被赋予一个随机的速度矢量。算法开始后每个粒子的速度和位置按一定规则迭代更新,迭代公式如下:
vk+1i=ωvki+c1rand1()(pbesti-xki)+c2rand2()(gbestk-xki);(11)
xk+1i=vk+1i+xki。(12)
式中:Vki表示第k次迭代中第i个粒子的速度;Xki表示第k次迭代中第i个粒子的位置。pbestk代表第i个粒子迭代开始后找到的最优位置;gbestk为第k次迭代后群体中所有粒子曾经搜索到的最优位置,由每次迭代后各粒子相互交换信息得到。关于最优位置的判定,由适应值函数决定,算法的目的是寻找区域内适应值最大或最小的点,适应值函数与要解决的问题有关,将在第三章中介绍。ω被称为惯性因子,c1、c2为正值常数。式(11)中还有2个随机数rand,代表在区间[0,1]上的随机数,用来增加搜索的随机性。在算法执行初期,粒子由于初始被赋予随机的位置和速度会在区域各处搜索,随后由于某些个体发现了一些较优解开始聚集,最终绝大部分粒子会收敛到一个位置,该位置就是PSO算法得出的区域内的最优解。
2.2 对PSO算法的改进
2.1节所述的PSO算法有一个缺陷:粒子有可能收敛到局部最优解,产生这种问题的原因可能是因为粒子在初期迭代的搜索范围没有覆盖到所有区域,或者粒子在迭代过程中收敛过快,以及PSO算法缺少能“跳出”局部最优解继续搜索的能力。2.1节所讲述的PSO算法中,粒子每次速度迭代公式中的gbest项为所有粒子比较后得到的历史最优解,可以理解为每个粒子在每次迭代中同时受到其他所有个体的影响,这种模式被称为全局PSO 算法,这种结构的PSO算法收敛速度最快,同样也更容易出现收敛到局部最优解的问题。
因此有学者提出改变粒子群的拓扑结构来应对过早收敛的问题,被称为PSO算法的局部版本相比于全局PSO算法中粒子速度受到所有其他个体的影响,局部PSO算法在速度更新公式中用Lbest代替gbest,即
vk+1i=ωvki+c1rand1()(pbesti-xki)+c2rand2()(Lbestk-xki)。(13)
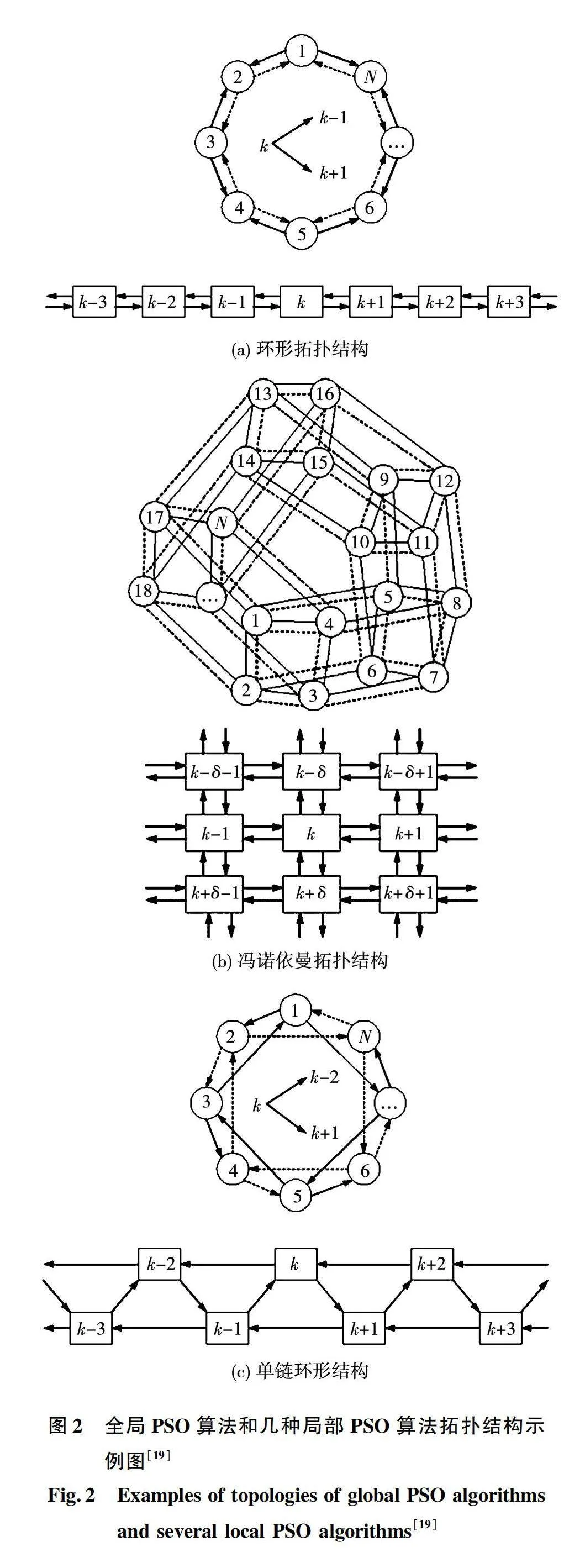
式中Lbest代表每个粒子的邻域中的粒子搜索到的最优位置,即每次迭代粒子只与邻域内的个体交流信息。局部PSO算法中粒子的速度迭代只会被邻域中的粒子影响,不同拓扑结构中邻域的粒子数量是变化的。例如最简单的环形拓扑结构[16],邻域粒子数量为2,整个拓扑结构为环形,粒子只受左右2个粒子的影响;冯诺依曼拓扑结构的邻域粒子数量为4,分别位于两侧和顶部底部[17];以及非对称的拓扑结构等[18]。上述的几种拓扑结构如图2所示。以上这些算法只是邻域构成不同,粒子群的拓扑结构不同,实际上算法原理是相同的。邻域中粒子的个体数量越多,信息在群体中的传输越快,收敛速度越快。
局部PSO算法本质上是减慢了信息在群体中传递的速度,降低了收敛速度,让粒子群体的复杂度在初期保持较高水平,能够尽可能搜索区域中的所有位置。在图2中所示的3种拓扑结构中,环形拓扑结构个体间联系最少信息传输最慢,收敛速度最慢[17];冯诺依曼结构和单链环结构收敛速度近似,但是冯诺依曼结构算法实现相对简单。因此综合收敛速度和算法实现难易度,选择冯诺依曼结构,该结构中粒子的邻域中有4个粒子。
3 基于PSO的PID控制器实现
3.1 基于PSO算法的PID控制器实现
在无刷电机控制领域,为了满足控制的精确度和稳定性,经常用到磁场导向控制技术(field-oriented control,FOC)(又称矢量控制)。矢量控制的基本思想是将电机三相电流在磁场坐标系下分解,磁场坐标系以转子磁链方向为参考方向。依据这个参考系,将定子电流分解为与转子磁链同方向的定子电流励磁分量(Id)和与磁链方向正交的定子电流转矩分量(Iq)。这样就将三相交流电机的电流控制问题转变为2个独立轴上的磁场和电流控制问题,控制过程中满足定子电流励磁分量(Id)为0,定子电流转矩分量(Iq)为常数且与转速正相关。
电机的矢量控制系统中,如果要实现对电机的速度控制,一般采用速度环嵌套电流环的设计方法。电流环是对FOC算法中的电流Id、Iq进行控制,进而控制电机转矩。电流环的作用在于使电机以最大电流启动并快速恢复到参考值,加快响应速度,提高系统稳定性。速度环在维持电流参考值的基础上,控制电机转速,速度环设计合理的话,可以进一步降低外部扰动对系统的影响,减小转速波动,输出稳定的力矩。
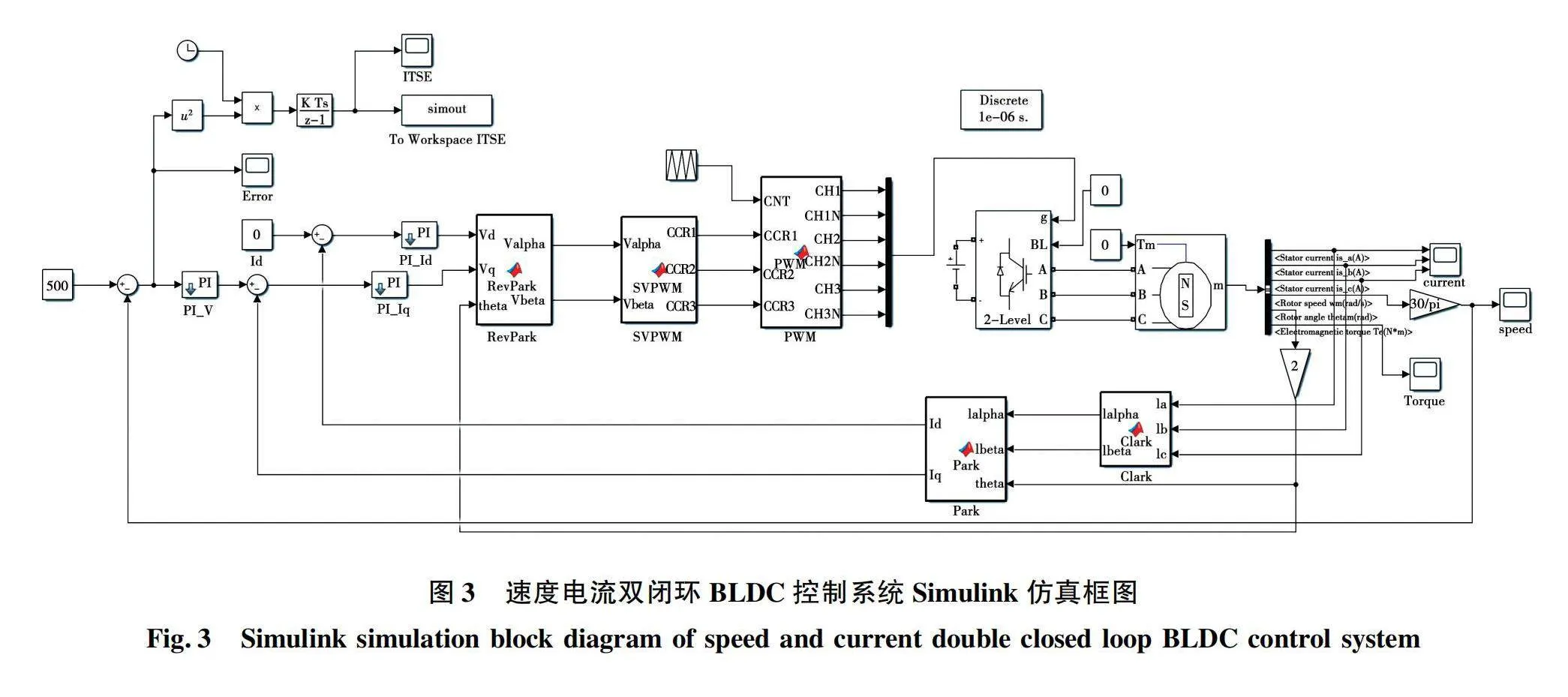
从上文中对PSO的算法介绍中,不难看出PSO的目的就是寻找目标函数在一定范围中的最小值(或最大值)。将这种方法应用在对 BLDC的PID控制器优化中。研究的对象是一个采用矢量控制技术的速度电流双闭环电机控制系统,如图3所示。
图3的控制系统中内环和外环都使用的是PI控制器,使用PI控制器而不是PID控制器的原因是在式(1)中电机模型一般被认为是“电阻+电感”的模型,为了抵消电感的作用,大都使用PI控制器,此外在强调快速动态响应的离散控制系统中,微分环节会放大噪声,对系统产生负面影响。该系统的内环是电流环,即FOC中经过帕克变换的电流值Id和Iq;外环是速度环,控制电机的转速。
在该系统中,外环的速度环有一个PI控制模块,内环电流环有2个PI控制模块对Id、Iq 2个电流分别进行控制,即共有6个参数需要调节,如果采用手动调整PI参数的方法来优化性能,过程过于繁琐和重复。因此采用优化PSO算法对控制系统的PI参数进行整定。目的是使用PSO算法找到一组PI参数使电机的性能最优,因此采用在PID控制器设计方法中常见的性能指标:时间加权积分平方误差(integral time square error,ITSE)[20-23] 作为电机性能的量化参考值,如下式:
ITSE=∫∞0t[r(t)-y(t)]2dt=∫∞0te2(t)dt。(14)
其中e代表目标值与实际值的误差。ITSE越小,代表电机的速度曲线越符合目标速度曲线,通过PSO算法找到使ITSE为最小值的解,即认为找到电机性能最优的情况,实现对电机控制系统的参数整定。
3.2 算法流程介绍
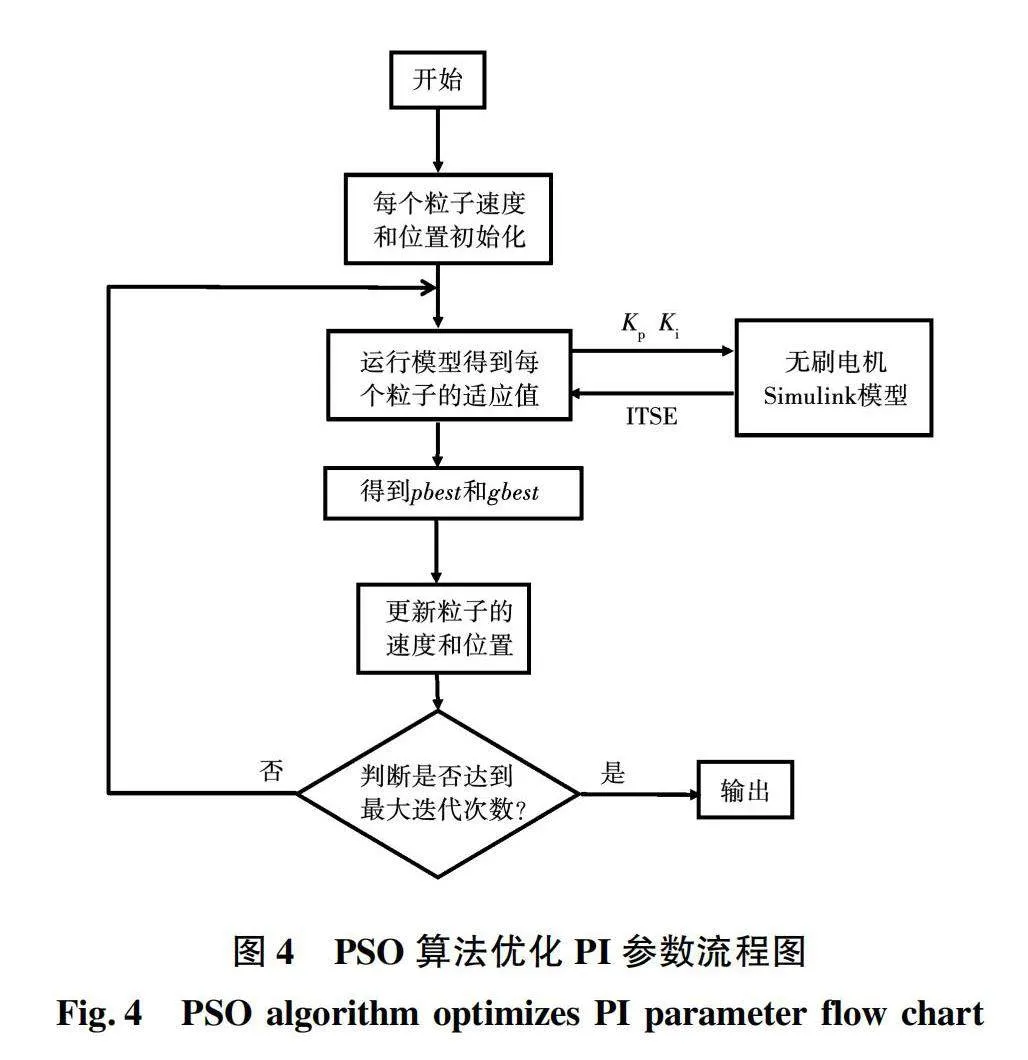
将内外环的PI参数(共6个)作为粒子的坐标,使粒子群在一个六维空间中进行搜索。PSO算法的实现流程如图4所示:1)初始化每个粒子的位置和速度,通常粒子的初始速度和初始位置在限定范围内随机生成。2)计算每个粒子的适应值(每个粒子的坐标就是一组PI参数,这组参数下电机的性能指标即式(14)的ITSE值为适应值)。3)每个粒子当前搜索到的最优位置称为个体历史最优位置(pbest),所有粒子的pbest比较后整个粒子群搜索到的最优位置称为群体历史最优位置(gbest)。每次计算适应值后都要更新个体历史最优位置和群体历史最优位置。4)如果没有达到最大迭代次数就继续下一次迭代。
4 仿真实验结果和分析
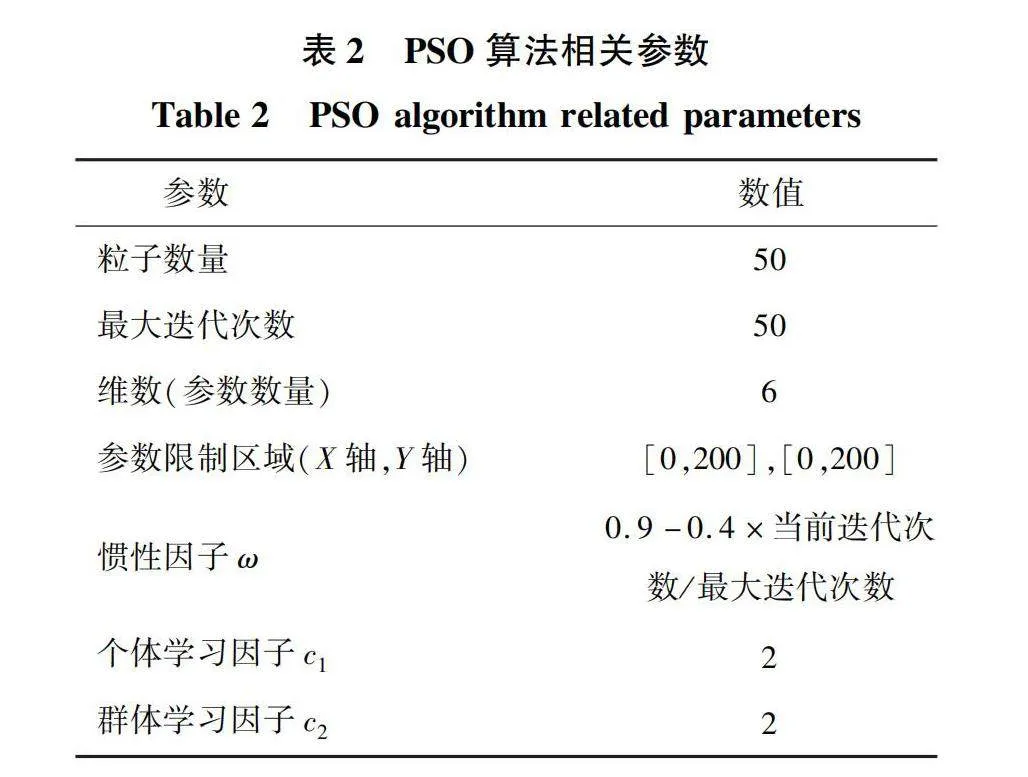
后续实验以图3所示的BLDC闭环控制系统Simulink模型为平台,模型中的电机参数如表1所示,后续实验所用到的优化PSO算法的相关参数如表2所示。根据图4的流程执行算法,由电机Simulink模型返回的ITSE指标为参数,进行优化计算,最终得到一组解,即内环和外环PI控制器的参数,再将这组参数带入模型,得到速度和输出力矩随时间的变化情况。
4.1 静态/动态目标速度值下的速度响应
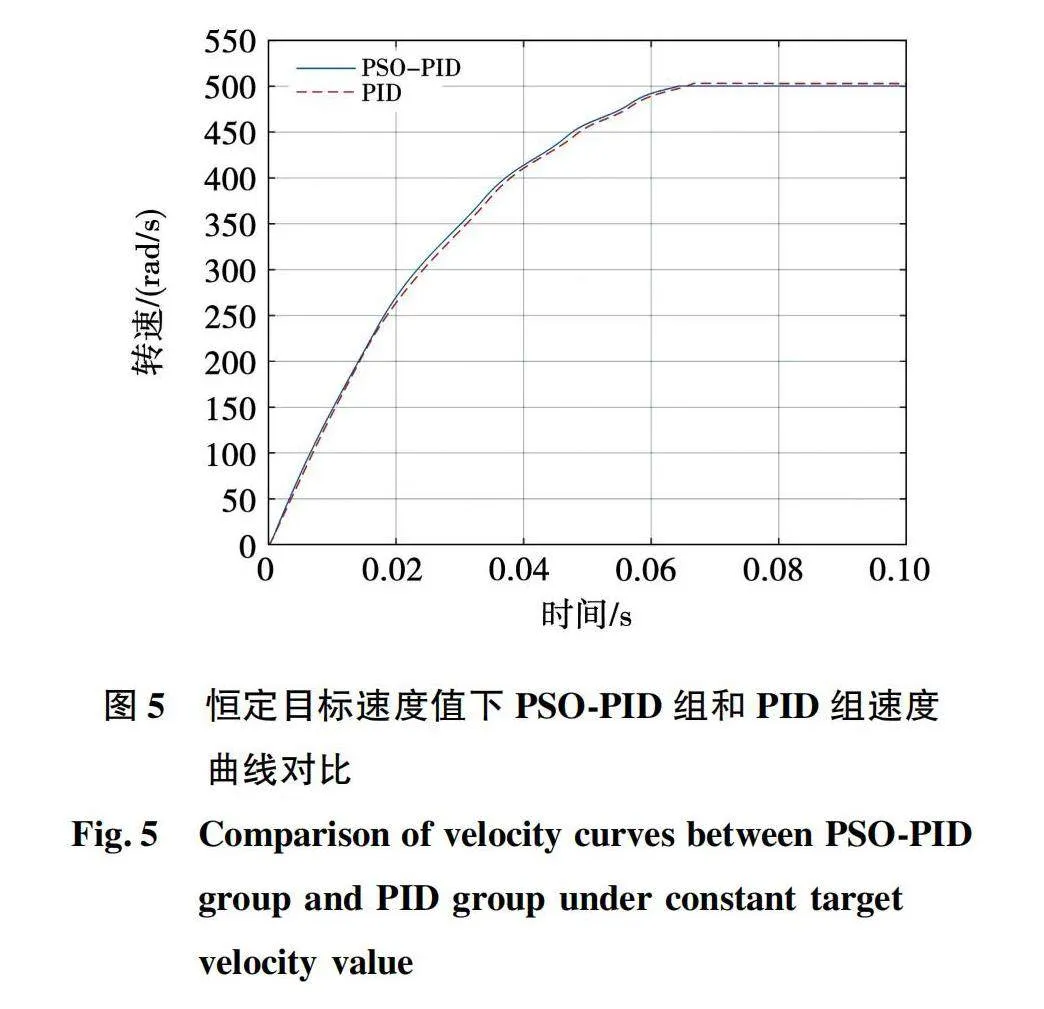
首先在目标速度为固定值的情况下,对优化PSO算法得到的结果(PSO-PID组)和传统PID调参方法得到的结果(PID组)进行对比。传统PID调参采用Ziegler-Nichols方法[24],先打开外环调整内环参数,内环稳定后再调整外环参数,在PI参数确定过程中使用Ziegler-Nichols方法中的临界比例法。Ziegler-Nichols方法是一种应用在各种工业过程控制系统中的经典调优方法[25],其优点在于只需要找到系统的临界增益和临界周期,使用特定的公式可以计算控制器参数,其步骤简单明了。通常能保证系统在获得适当响应速度和稳定性之间取得平衡,有助于减少超调和缩短调整时间。最终得到的参数为:速度环P=7,I=20;电流环P=5,I=80。此时目标速度为500 r/min,记录两组在0~0.1 s下的速度曲线如图5所示。
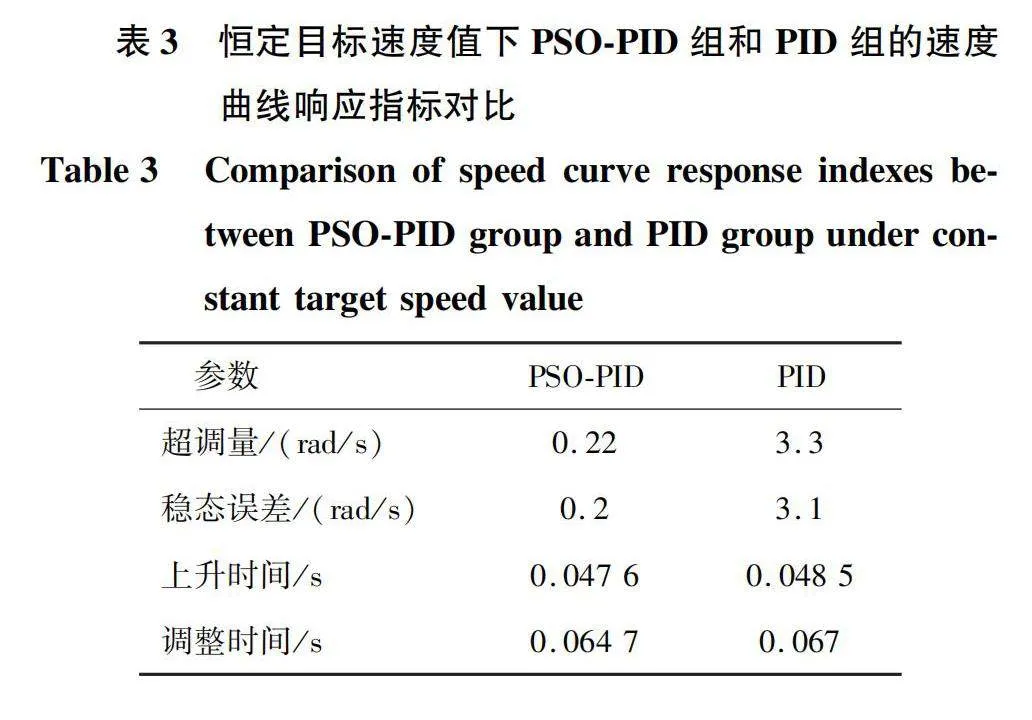
由图5可以看到,优化PID算法得到的结果有更快的响应速度和更小的稳态误差,并且在其他方面也优于传统的PID方法。具体的指标总结如表3所示,总结了两组速度曲线的超调量、稳态误差、上升时间和调整时间。其中上升时间为输出响应达到90%稳态值所对应的时刻,调整时间为输出响应进入稳态误差范围所对应的时刻。
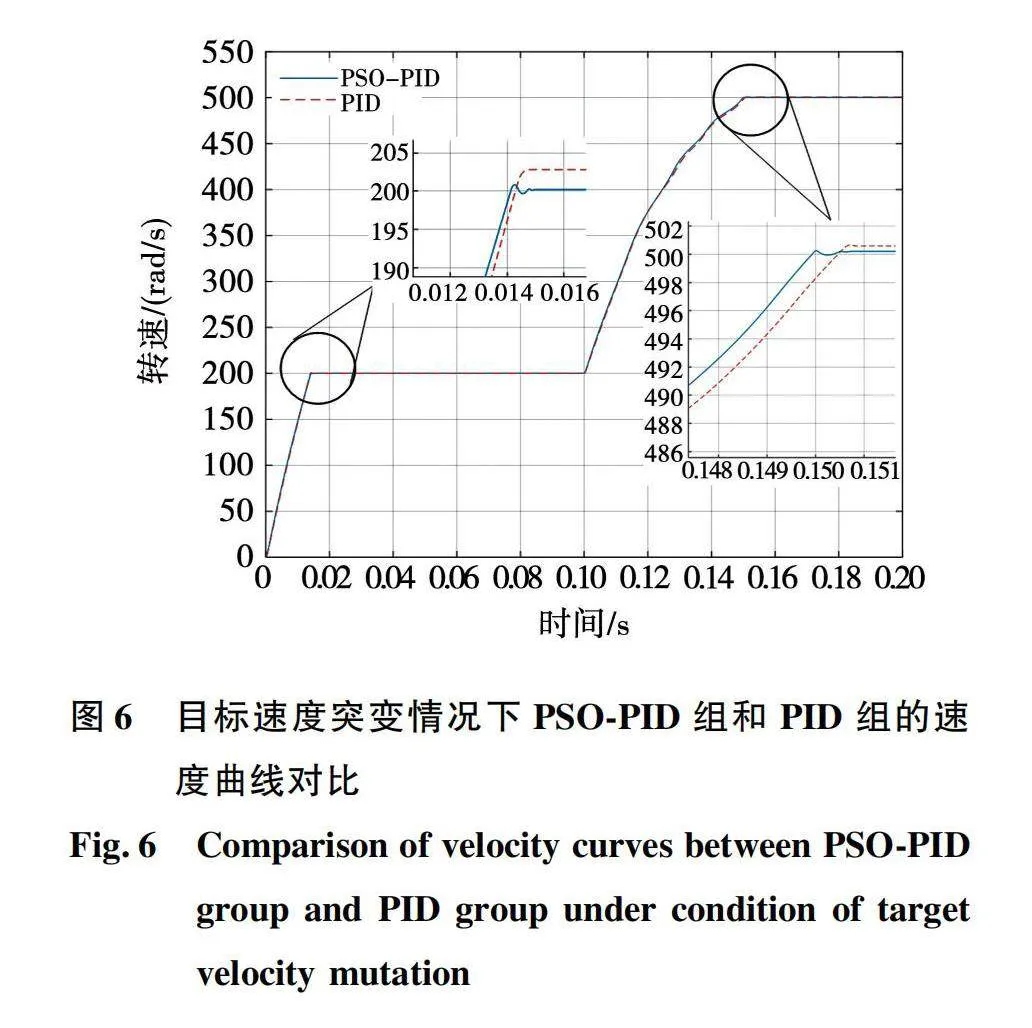
此外还测试了在目标速度发生突变的情况下的电机速度响应。在其他条件相同的情况下,速度参考值在0~0.1 s为200 r/min,在0.1 s时刻突变为500 r/min,记录优化PSO算法和PID方法两组在0~0.2 s下转速的变化情况如图6所示。
由图6可以得出,优化PSO算法整定的系统相比传统PID方法在目标速度的突变下表现出更好的动态响应能力,在仿真刚开始的阶段,相比于PID组,PSO-PID组有更小的超调量和稳态误差,同样在0.1 s速度参考值发生变化后,PSO-PID组的响应更为迅速,而且超调量和稳态误差依然优于PID组,反映在优化PSO算法整定下的电机控制系统在动态响应方面更加出色,系统的稳定性更好。
4.2 改进的PSO算法与基本PSO算法比较
2.2节介绍的局部版本的PSO算法相比于基本的PSO算法(称之为全局PSO算法)能够有效避免收敛到局部最优解,其原因是局部PSO算法在搜索初期,避免了粒子群的快速收敛使其尽可能遍历搜索范围。即保证了粒子群在算法过程中的多样性,种群多样性越高,表示粒子散布程度较高,这在搜索初期是有利的。因此将用实验验证局部PSO算法的粒子群多样性高于全局PSO算法,种群多样性的指标采用J指数[23] 衡量,如下式:
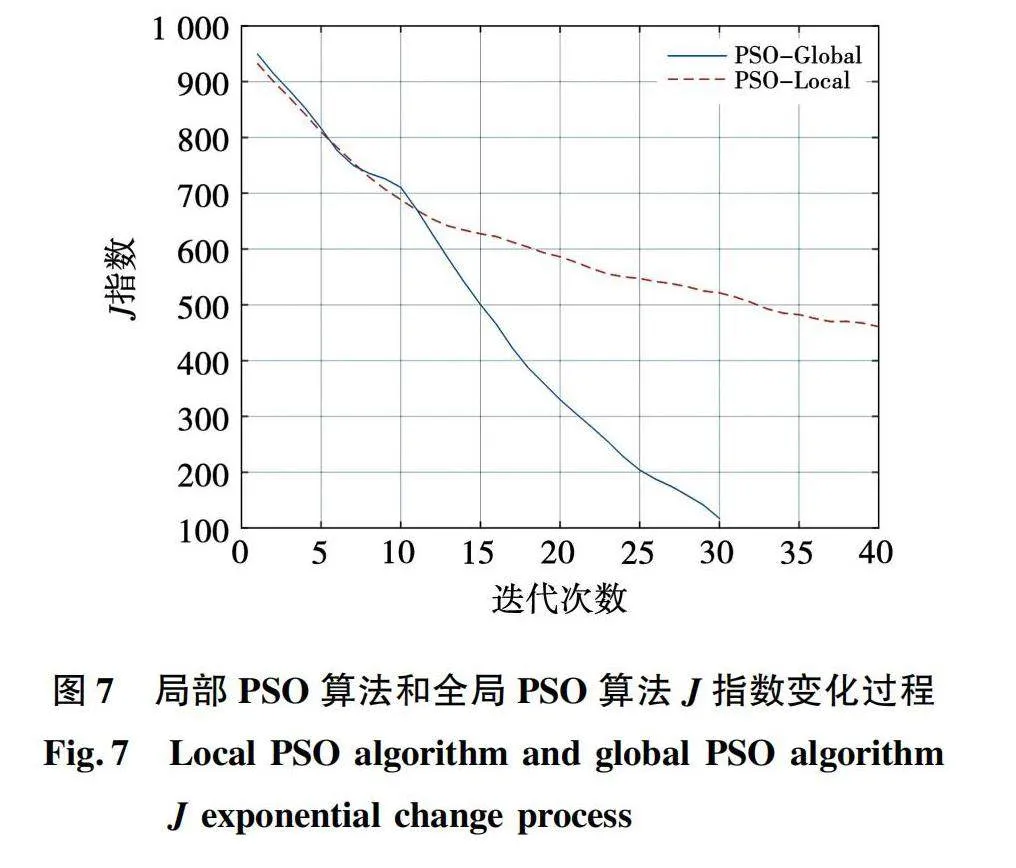
粒子越分散,J指数越大,表示种群的多样性越高。图7展示了局部PSO和全局PSO两种算法在过程中粒子种群多样性的变化。
从图7可以看出:初始状态下由于粒子为随机分布,此时两种算法的种群多样性相近,随着搜索不断进行,全局PSO算法多样性迅速下降,容易出现收敛到局部最优解的情况,PSO算法又缺少从局部最优解中跳出的能力,很容易对最终结果产生影响。局部PSO算法的种群多样性在前期一直以较慢的速度下降,使粒子群有时间能够遍历搜索区域,并且其缓慢平均的收敛速度在一定程度上避免了局部最优解的陷阱。
4.3 不同算法整定结果比较
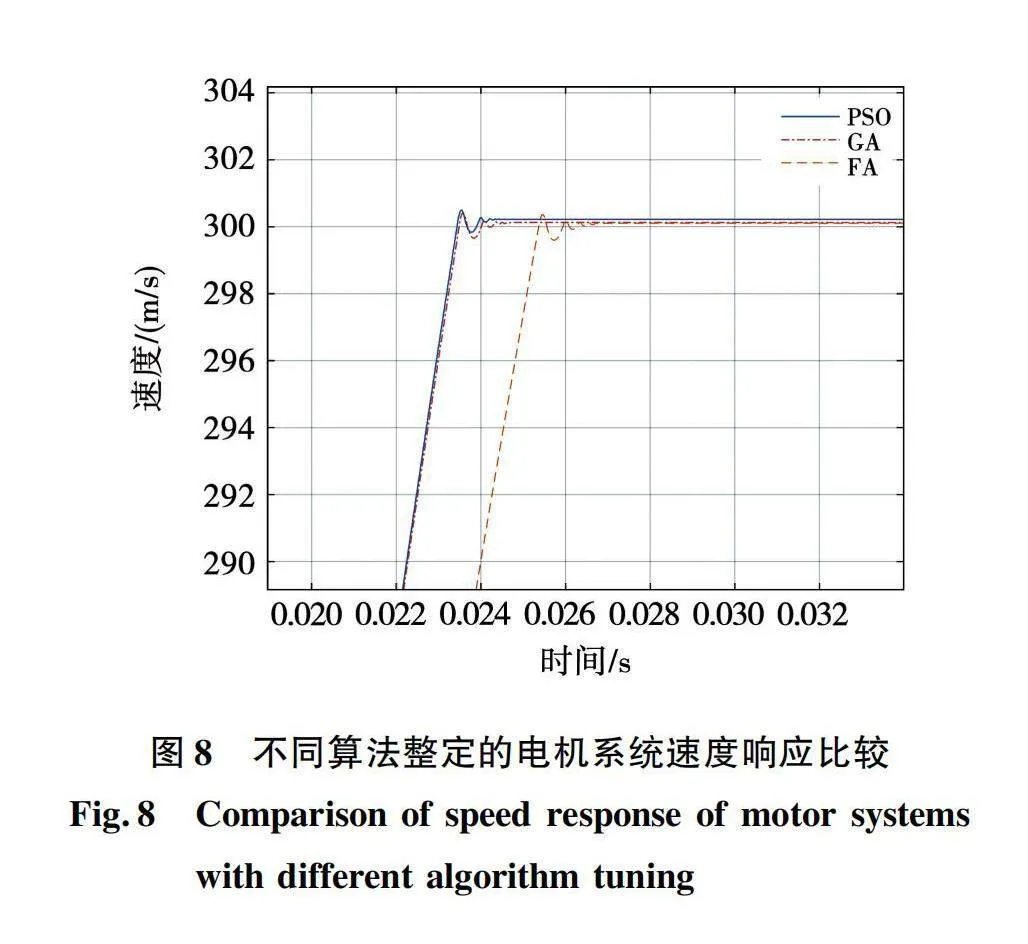
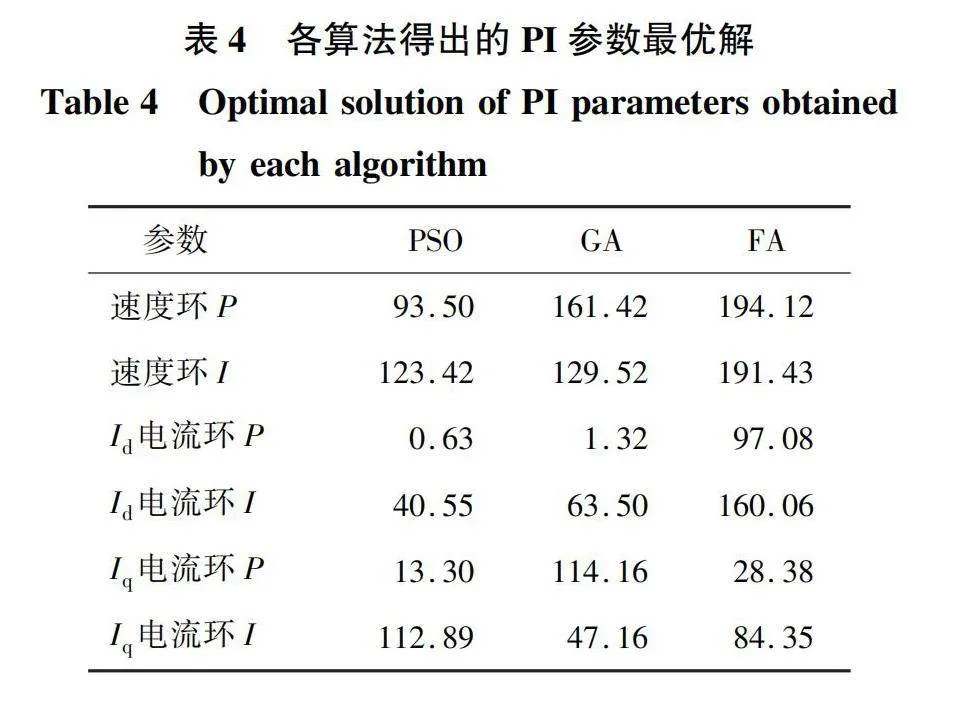
在PID参数自动整定方面,还有其他智能算法的应用。本节将PSO算法和其他智能算法得到的结果进行对比,分析各自的适用领域。各算法运行得到的电机系统PI参数如表4所示,将这些值带入电机Simulink模型进行仿真,得到电机的速度曲线,并与遗传算法(genetic algorithm,GA)[26]和萤火虫算法(firefly algorithm,FA)[12]得到的结果进行比较,结果如图8所示。
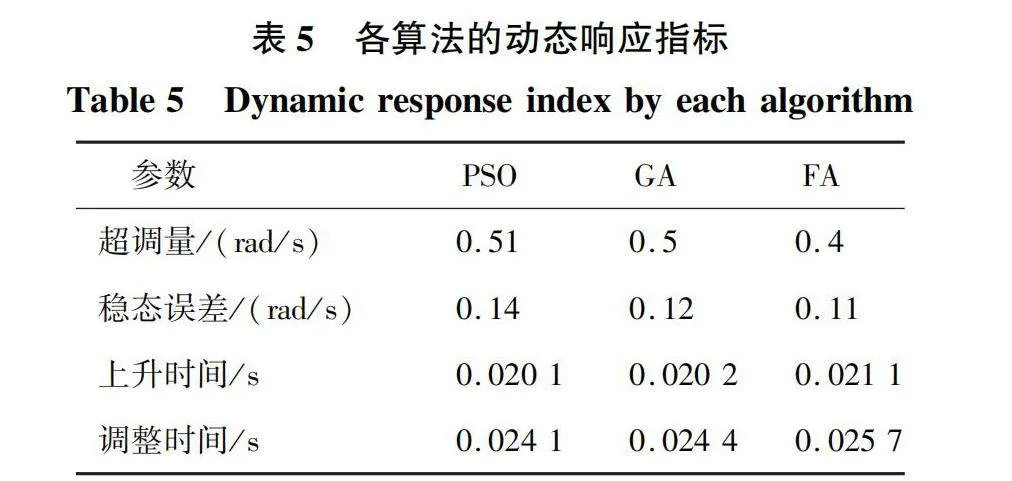
在目标速度恒定的条件下,分别对注入三组参数的电机系统进行仿真,目标速度300 r/min,图8中展示了优化PSO算法与其他智能算法整定的电机系统速度响应曲线,表5展示了速度动态响应的几项指标。结果对比可以看出PSO组的响应速度优于GA组和FA组,即对于一个恒定的速度目标值有更快的响应时间。在超调量方面和稳态误差方面,PSO组和GA组基本相等,FA组的表现略优,有更小的稳态误差和超调量。不同算法的整定结果各有优缺点,PSO算法整定的系统在系统动态响应方面表现出了优势,但在特定领域,还要根据问题的性质和需求选择最合适的优化算法。
4.4 电机输出力矩表现
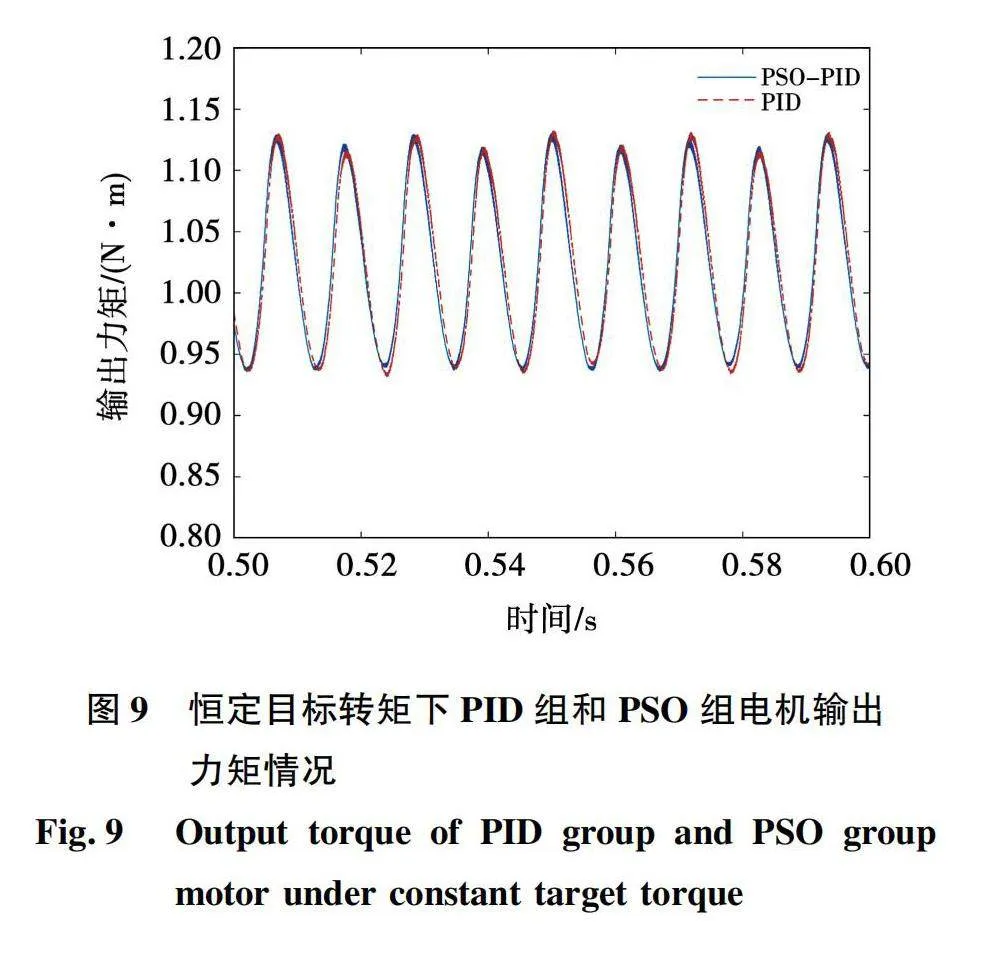
除了关注该电机控制系统在速度上的表现,也要关注电机的力矩输出表现,作为在姿控系统中使用的电机,力矩输出的精准度和稳定性是影响姿控系统性能的关键。通过测量电机在负载恒定和负载突变2种情况下的转矩脉动情况作为衡量力矩平稳程度的指标。转矩脉动是指转矩的最大值与最小值之差与转矩平均的比值,经常被用来衡量电机转矩表现,即
图9展示了在目标转矩为1 N·m和目标转速恒定的情况下,采用传统PID方法和PSO算法整定的电机系统在0.5~0.6 s内力矩输出情况。其中PID组的平均转矩为1.024 6 N·m,最大值为1.132 6 N·m,最小值为0.931 6 N·m,转矩脉动为19.62%;PSO组平均转矩为1.027 5 N·m,其中最大值为1.130 2 N·m,最小值为0.936 1 N·m,转矩脉动为18.89%。PSO组相比于PID组输出转矩有所减小,稳定性上也有提升,稳态下转矩脉动下降了0.8%。
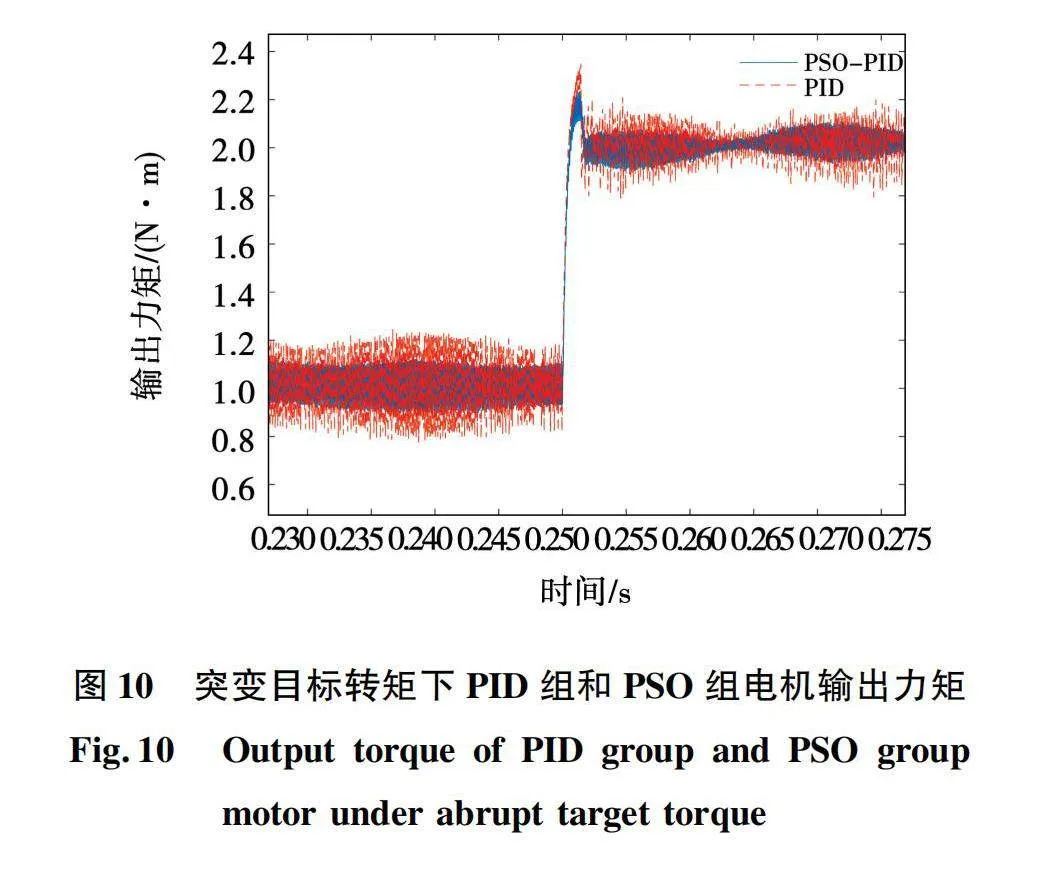
当电机的目标转矩发生突变时,PID组和PSO组的电机输出力矩表现如图10所示,其中目标转矩在开始时为1 N·m,在0.25 s突变为2 N·m。在0.25 s前,两组的表现与恒定目标转矩情况的表现基本一致,但在目标转矩发生突变后PSO组电机的输出转矩能够更快地调整到目标值附近,并且在稳定后PSO组的电机转矩峰峰值明显小于PID组,输出力矩更平稳,说明PSO算法整定的电机系统对于目标转矩值突变的情况有更强的适应能力。
在实际的卫星姿控系统中,还有前馈控制算法、角动量约束等方法使电机的控制精确度进一步提高,本节实验只是对闭环电机控制系统做一个简要的仿真,虽然在某些方面性能提升的幅度并不明显,但足以证明结合了PSO算法的PI控制器相比于传统的PI控制器具有力矩波动小、响应迅速等优点。
4.5 电机参数变化对PSO整定方法的影响
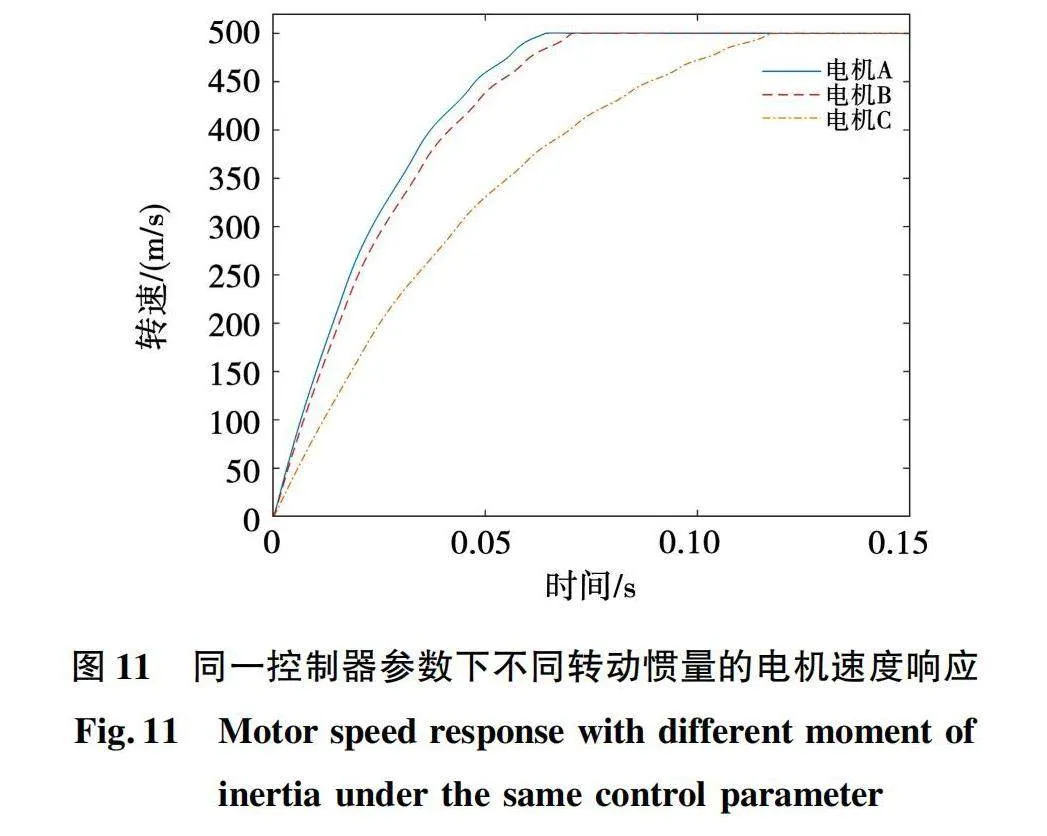
卫星上的电机参数各不相同,当一个电机的PI控制器参数通过PSO算法标定完成后,同类型但参数有变化的电机是否可以使用相同的PI控制器参数进行控制以减小标定次数,本节将通过实验进行讨论。此前的实验中标定对象为表1所示参数的电机(命名为电机A),将电机A转动惯量增加10%后的电机命名为电机B,将电机A转动惯量增加85%的电机命名为电机C。3个电机的控制系统都使用电机A的PI控制器参数进行控制,得到如图11的速度响应曲线对比。
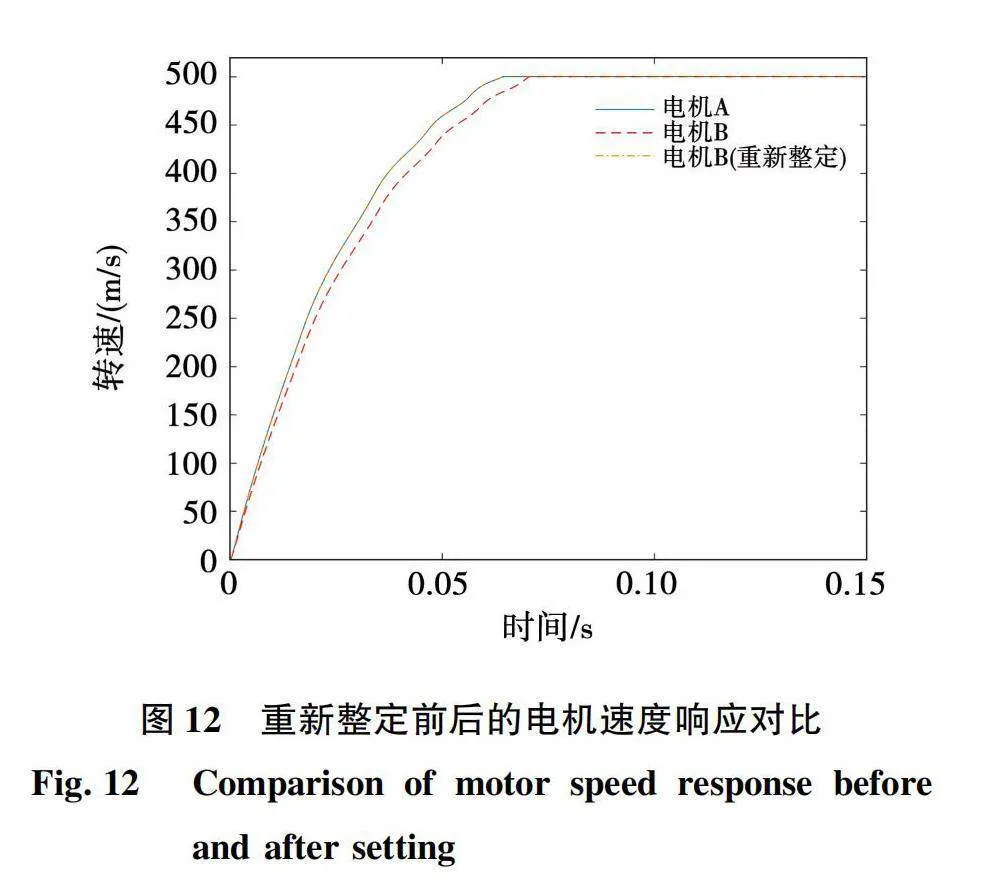
由图11所示,电机转动惯量的增加使电机的速度响应变慢,参数改变幅度越多,电机的速度响应效果越差。转动惯量增加10%的电机B与电机A的差距并不明显,但转动惯量增加85%的电机C与电机A的差距已相当明显。产生这种差距的原因可能是电机的转动惯量增加导致电机的“负载”增大影响响应速度,也可能是电机参数变化导致原来整定的结果不适用于新的电机。为了确定哪方面原因影响更多,继续进行如下实验:对电机B再次进行整定,整定得到新的PI数值,与采用电机A的PI数值的电机A和电机B进行比较,结果如图12所示。
可以看出对于电机B重新整定后的结果与采用电机A的PI数值几乎一致,两条曲线重合度非常高,可以认为图11中的偏差是由于转动惯量的增大引起的影响。在转动惯量发生10%左右的较小变化后,PSO算法整定的结果依然可以继续使用并具有较好的性能。
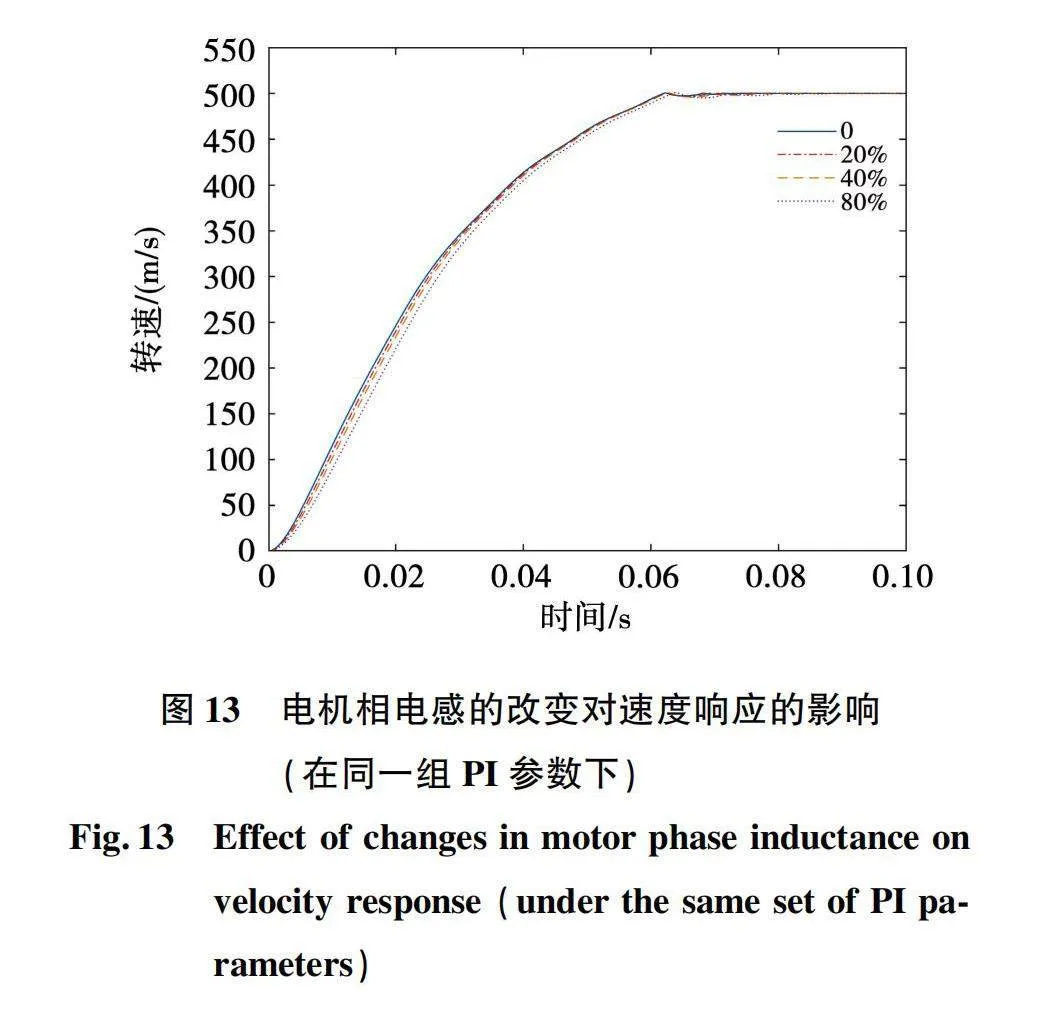
随后讨论电机相电感的改变对注入同一组PI参数的闭环控制系统的影响,图13中图例“0”组表示电机A的速度响应曲线,此外图中还有相电感在电机A的基础上分别增加20%、40%、80%后的电机速度曲线,目标速度为500 rad/s,从静止开始增速,图13展现了其他参数相同情况下不同相电感的电机速度响应曲线。
可以看出,电机相电感的增加导致整个系统的动态响应变慢,稳态误差增加。原因是电感增大,电机的时间常数增加,影响动态响应,导致上升速率变慢。此外,电流环的控制带宽会因为电感的增大而减小,电流环对高频干扰的抑制能力变差,影响整体速度控制的精确性。不过从图13来看,相电感的变化对整体速度响应曲线的影响比较小,电感增加后的电机仍可以在原参数下的系统快速达到目标速度,PSO算法的结果依然可以使用并得到较好结果。
不过在实际工程应用中,微纳卫星上搭载的电机大都用于姿态控制系统或可变形部件,其主要作用是输出力矩,因此星上同类型电机中不同个体的主要差别体现在电机和带载物体的转动惯量上。通过调整电机上携带的质量块的重量和分布可以很容易的改变电机的负载或调整转子的转动惯量,而改变其他变量如电机电感、相电阻、反电动常数等需要对电机结构进行改变,实现上较为复杂。
结合以上实验可以得出:对于同一类型但某些参数有差异的众多电机可以通过一次标定的方法解决,减小了标定PI参数所需时间和次数。另一方面,可以通过上述实验确定无刷电机的哪些参数是影响电机性能的关键参数,以这些关键参数的不同作为指标进行分类标定和重点分析。
5 结 论
针对传统PID控制器控制无刷电机时系统响应慢、速度波动大和手动调节大规模电机参数繁琐重复的问题,本文引入了局部版本的PSO算法,以电机的速度误差累计作为指标,将PSO模型与PI控制器相结合,对无刷电机控制系统的PI参数进行了优化。结果表明:
1)经过优化PSO算法优化的电机控制系统相比于传统PID控制器速度响应更快,稳态误差更小,力矩输出方面更稳定,并且参数整定过程相比于手动调整PID参数更迅速。
2)在本文方法中,电机某些参数的较小改变对电机控制系统的整定结果和系统响应影响很小,因此该整定方法对同类型参数相似的一类电机的PI控制器参数优化有较好效果,可以应用在同类型大批量的电机参数标定中。
该整定方法解决了传统PID控制器在控制无刷电机中系统响应慢,稳态误差和超调量大等问题。同时为微纳卫星集群中大规模同类型电机调参标定需求提出了一种解决方法。
参 考 文 献:
[1]CHO M, HIROKAZU M, GRAZIANI F. Introduction to lean satellite and ISO standardfor lean satellite [C]//2015 7th International Conference on Recent Advances in Space Technologies (RAST), June 16-19, 2015, Istanbul, Turkey. 2015: 789-792.
[2]刘林, 曹鑫, 钱梦飞, 等. 永磁同步电机电流环PI控制器参数整定及优化[J].电机与控制学报,2023,27(10):131.
LIU Lin, CAO Xin, QIAN Mengfei, et al. Parameter setting and optimization of current ring PI controller of permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(10): 131.
[3]孙欣, 肖曦, 韩继文, 等. 基于机械参数辨识的永磁同步电机驱动系统速度环自调试方法[J].电机与控制学报, 2022, 26(12): 1.
SUN Xin, XIAO Xi, HAN Jiwen, et al. Speed loop self-commissioning for permanent magnet synchronous motor drives based on mechanical parameter identification[J]. Electric Machines and Control, 2022, 26(12): 1.
[4]LIAO Wudai, HU Yingyue, WANG Haiquan. Optimization of PID control for DC motor based on artificial bee colony algorithm[C]//Proceedings of the 2014 International Conference on Advanced Mechatronic Systems, August 10-12, 2014, Kumamoto, Japan. 2014: 23-27.
[5]RAHIDEH A, KORAKIANITIS T. Brushless DC motor design using harmony search optimization[C]//The 2nd International Conference on Control, Instrumentation and Automation, December 27-29, 2011,Shiraz, Iran. 2011: 44-50.
[6]ZHANG Jinhua, ZHUANG Jian, DU Haifeng. Self-organizing genetic algorithm based tuning of PID controllers[J]. Information Sciences, 2009, 179(7): 1007.
[7]RAO K S R, OTHMAN A H B. Design optimization of a BLDC motor by genetic algorithm and simulated annealing[C]//2007 International Conference on Intelligent and Advanced Systems, November 25-28, 2007, Kuala Lumpur, Malaysia. 2007: 854-858.
[8]RIDWAN M, RIAWAN D C, SURYOATMOJO H. Particle swarm optimization-based BLDC motor speed controller with response speed consideration[C]//2017 International Seminar on Intelligent Technology and Its Applications (ISITIA), August 28-29, 2017, Surabaya, Indonesia. 2017: 193-198.
[9]边琦, 马建, 张梦寒, 等. 改进细菌觅食算法的永磁同步电机参数辨识[J]. 电机与控制学报, 2024, 28(2):174.
BIAN Qi, MA Jian, ZHANG Menghan, et al. Parameter identification of permanent magnet synchronous motor based on modified bacterial foraging algorithm[J]. Electric Machines and Control, 2024, 28(2): 174.
[10]CHIHA I, LIOUANE N, BORNE P. Tuning PID controller using multiobjective ant colony optimization[J]. Applied Computational Intelligence and Soft Computing, 2012, 2012: 11.
[11]SHI Jun, MI Qingtao, CAO Weifeng, et al. Optimizing BLDC motor drive performance using particle swarm algorithm-tuned fuzzy logic controller[J]. SN Applied Sciences, 2022, 4(11): 293.
[12]BAZI S, BENZID R, BAZI Y, et al. A fast firefly algorithm for function optimization: application to the control of BLDC motor[J]. Sensors, 2021, 21(16): 5267.
[13]WANG Tingting, WANG Hongzhi, WANG Chuhang, et al. A novel PID controller for BLDCM speed control using dual fuzzy logic systems with HSA optimization[J]. Scientific Reports, 2022, 12(1): 11316.
[14]MILANI M M R A, ĢAVDAR T, AGHJEHKAND V F. Particle swarm optimization—based determination of Ziegler-Nichols parameters for PID controller of brushless DC motors[C]//2012 International Symposium on Innovations in Intelligent Systems and Applications, July 2-4, 2012, Trabzon, Turkey. 2012: 1-5.
[15]KENNEDY J. The particle swarm: social adaptation of knowledge[C]//Proceedings of 1997 IEEE International Conference on Evolutionary Computation (ICEC'97), April 13-16, 1997, Indianapolis, IN, USA. 1997: 303-308.
[16]KENNEDY J, MENDES R. Neighborhood topologies in fully informed and best-of-neighborhood particle swarms[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2006, 36(4): 515.
[17]KENNEDY J, MENDES R. Population structure and particle swarm performance[C]//Proceedings of the 2002 Congress on Evolutionary Computation (CEC’02), May 12-17, 2002, Honolulu, HI, USA. 2002, 2: 1671-1676.
[18]MUOZ ZAVALA A E, HERNNDEZ AGUIRRE A, VILLA DIHARCE E R. The singly-linked ring topology for the particle swarm optimization algorithm[C]//Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation, July 8-12, 2009, Montreal, Québec, Canada. 2009: 65-72.
[19]MUOZ ZAVALA A E. A comparison study of PSO neighborhoods[M]. Berlin, Heidelberg:Springer Berlin Heidelberg, 2013: 251-265.
[20]KROHLING R A, REY J P. Design of optimal disturbance rejection PID controllers using genetic algorithms[J]. IEEE Transactions on Evolutionary Computation, 2001, 5(1): 78.
[21]MITSUKURA Y, YAMAMOTO T, KANEDA M. A design of self-tuning PID controllers using a genetic algorithm[C]//Proceedings of the 1999 American Control Conference, June 2-4, 1999, San Diego, CA, USA. 1999: 1361-1365.
[22]KROHLING R A, JASCHEK H, REY J P. Designing PI/PID controllers for a motion control system based on genetic algorithms[C]//Proceedings of 12th IEEE International Symposium on Intelligent Control, July 16-18, 1997, Istanbul, Turkey. 1997: 125-130.
[23]ZHOU Dawei, GAO Xiang, LIU Guohai, et al. Randomization in particle swarm optimization for global search ability[J]. Expert Systems with Applications, 2011, 38(12): 15356.
[24]ASTROM K J, HAGGLUND T. Revisiting the Ziegler—Nichols step response method for PID control[J]. Journal of Process Control, 2004, 14(6): 635.
[25]LIU Yuqi, HUANG Yuanfeng, XIONG Bin, et al. Speed balance control of the dual-motor system based on three-vector model prediction[C]//International Conference on Electrical and Information Technologies for Rail Transportation, October 19-21, 2023, Beijing, China. 2023: 404-412.
[26]LIN Chunliang, JAN H Y, SHIEH N C. GA-based multiobjective PID control for a linear brushless DC motor[J]. IEEE/ASME Transactions on Mechatronics, 2003, 8(1): 56.
(编辑:刘琳琳)
